La materia ordinaria se presenta en alguno de los tres estados siguientes: sólido, líquido o gaseoso. Existe un cuarto estado de la materia denominado plasma que es esencialmente un gas ionizado con igual número de cargas positivas que negativas.

Un sólido cristalino es aquél que tiene una estructura periódica y ordenada, como consecuencia, tiene una forma que no cambia, salvo por la acción de fuerzas externas. Cuando se aumenta la temperatura, los sólidos se funden y cambian al estado líquido. Las moléculas ya no permanecen en posiciones fijas, aunque las interacciones entre ellas sigue siendo suficientemente grande para que el líquido pueda cambiar de forma sin cambiar apreciablemente de volumen, adaptándose al recipiente que lo contiene.

En el estado gaseoso, las moléculas están en continuo movimiento y la interacción entre ellas es muy débil. Las interacciones tienen lugar, cuando las moléculas chocan entre sí. Un gas se adapta al recipiente que lo contiene pero trata de ocupar todo el espacio disponible.

Densidad de un fluido

La densidad de una sustancia se define como el cociente de su masa entre el volumen que ocupa.

${\displaystyle \rho =\frac{m}{V}}$

La unidad de medida en el S.I. de Unidades es kg/m³, también se utiliza frecuentemente la unidad g/cm³

Densidad de sólidos y líquidos a (20ºC)

Fuente: Manual de Física Elemental. Koshkin N. I., Shirkévich M. G.. Edtorial Mir (1975) (págs. 36-37).

Concepto de presión

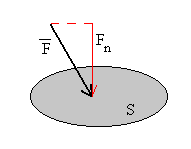
Se define presión como el cociente entre la componente normal de la fuerza sobre una superficie y el área de dicha superficie.

${\displaystyle p=\frac{F_n}{S}}$

La unidad de medida recibe el nombre de pascal (Pa).

La fuerza que ejerce un fluido en equilibrio sobre un cuerpo sumergido en cualquier punto es perpendicular a la superficie del cuerpo. La presión es una magnitud escalar y es una característica del punto del fluido en equilibrio, que dependerá únicamente de sus coordenadas como veremos en la siguiente página.

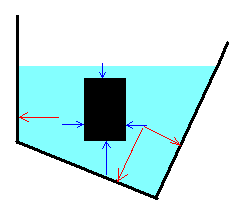
En la figura, se muestran las fuerzas que ejerce un fluido en equilibrio sobre las paredes del recipiente y sobre un cuerpo sumergido. En todos los casos, la fuerza es perpendicular a la superficie, su magnitud y el punto de aplicación se calculan a partir la ecuación fundamental de la estática de fluidos.

Los hemisferios de Magdeburgo

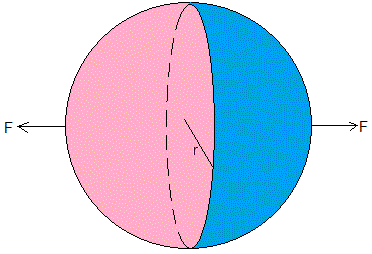
Los hemisferios de Magdeburgo son dos semiesferas de cobre que se acoplan formando una esfera hueca de radio r de cuyo interior se extrae el aire. Supongamos que la presión en el interior es p_i=0.1 atm. La diferencia de presión entre el interior y el exterior de la esfera es Δp=0.9 atm. Vamos a calcular la fuerza F necesaria para separar las dos semiesferas

El área del elemento de superficie esférica comprendido entre θ y θ+dθ es dS=(2πrsinθ)r·dθ

La fuerza que ejerce la diferencia de presión Δp sobre esta superficie es dF=Δp·dS y tiene dirección radial

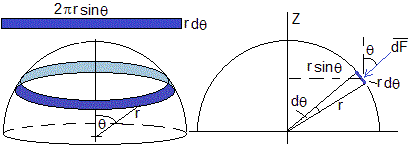
Por simetría, las componenentes horizontales de la fuerza, se anulan. Su componente vertical es -dFcosθ. La fuerza sobre una semiesfera es

${\displaystyle \begin{array}{l}F=-{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\left(\Delta p·2\pi r^2\sin \theta ·d\theta \right)}\cos \theta =-2\pi r^2\Delta p{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\sin \theta ·\cos \theta ·d\theta }=\\ -\pi r^2\Delta p{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\sin 2\theta ·d\theta }=-\frac{1}{2}\pi r^2\Delta p{\cos 2\theta |}_0^{\pi /2}=-\pi r^2\Delta p\end{array}}$

Si la diferencia de presión que mantiene las semiesferas unidas es Δp=0.9 atm y el radio de la esfera es r=30 cm. La fuerza que tenemos que ejercer sobre cada una de las semiesferas para separarlas es F=Δp·πr²

F=π0.3²·1.013·10⁵·0.9=25 778 N

Variación de la presión con la profundidad

Consideremos una porción de fluido en equilibrio de altura dy y de sección S, situada a una distancia y del fondo del recipiente que se toma como origen.

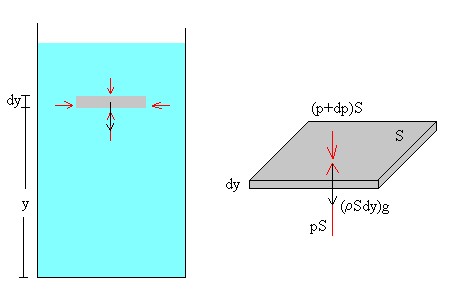
Las fuerzas que mantienen en equilibrio a dicha porción de fluido son las siguientes:

• El peso, que es igual al producto de la densidad del fluido, por su volumen y por la intensidad de la gravedad, (ρ·S·dy)g.
• La fuerza que ejerce el fluido sobre su cara inferior, p·S
• La fuerza que ejerce el fluido sobre su cara superior, (p+dp)S

La condición de equilibrio establece que

(ρ S·dy)g+pS=(p+dp)S

dp=-ρ·g·dy

${\displaystyle \frac{dp}{dy}=-\rho g}$

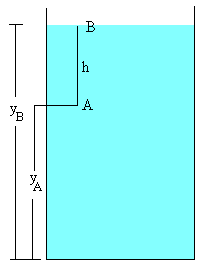
Integrando esta ecuación entre los límites que se indican en la figura

${\displaystyle {\displaystyle \underset{p_A}{\overset{p_B}{\int }}dp}={\displaystyle \underset{y_A}{\overset{y_B}{\int }}-\rho gdy}{p}_B-p_A=\rho g{y}_A-\rho g{y}_B}$

Situamos el punto B en la superficie y el punto A a una profundidad h. Si p₀ es la presión en la superficie del fluido (la presión atmosférica), la presión p a la profundidad h es

p=p₀+ρgh

Medida de la presión. Manómetro

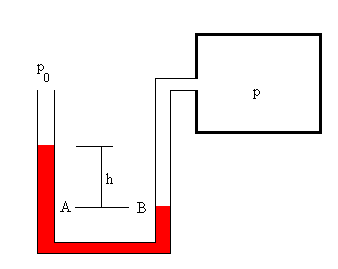
Para medir la presión empleamos un dispositivo denominado manómetro. Como A y B están a la misma altura la presión en A y en B debe ser la misma. Por una rama la presión en B es debida al gas encerrado en el recipiente. Por la otra rama la presión en A es debida a la presión atmosférica más la presión debida a la diferencia de alturas del líquido manométrico.

p=p₀+ρgh

Experiencia de Torricelli

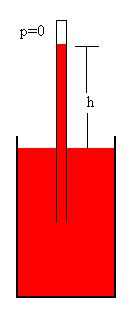
Para medir la presión atmosférica, Torricelli empleó un tubo largo, cerrado por uno de sus extremos, lo llenó de mercurio y le dio la vuelta sobre una vasija de mercurio. El mercurio descendió hasta una altura h=0.76 m al nivel del mar. Dado que el extremo cerrado del tubo se encuentra casi al vacío p=0 y sabiendo la densidad del mercurio es 13.55 g/cm³ ó 13550 kg/m³ el valor de la presión atmosférica es

${\displaystyle p=\rho gh=13550\cdot 9.81\cdot 0.76=101023\text{ Pa}}$

Fuerza sobre el muro de un embalse

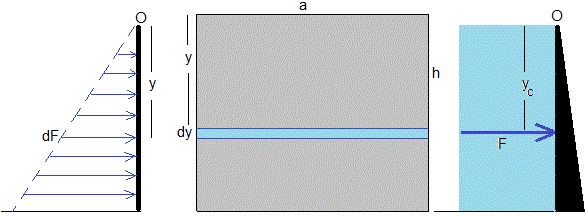
Sea el muro de un embalse de longitud a y de altura h. La fuerza dF que ejerce la presión del agua sobre un elemento de área a·dy situado a una profundidad y, es dF=ρgy(a·dy)

La fuerza total sobre el muro es

${\displaystyle F={\displaystyle \underset{0}{\overset{h}{\int }}\rho gay·dy}=\frac{1}{2}\rho ga{h}^2}$

El momento de las fuerzas respecto del punto O es

${\displaystyle M={\displaystyle \underset{0}{\overset{h}{\int }}y·\left(\rho gay·dy\right)}=\frac{1}{3}\rho ga{h}^3}$

El momento de la resultante F respecto de O es

${\displaystyle \begin{array}{l}\left(\frac{1}{2}\rho ga{h}^2\right)y_c=\frac{1}{3}\rho ga{h}^3\\ y_c=\frac{2}{3}h\end{array}}$

y_c es la posición de la resultante F de las fuerzas que actúan sobre el muro debido a la presión del agua.

Actividades

En esta actividad comprobamos la ecuación fundamental de la estática de fluidos, es decir, que la presión varía linealmente con la profundidad.

Se conecta un tubo por un extremo a un manómetro y por el otro a un elemento o cápsula de presión consistente en un cilindro de metal con un diafragma de goma, dispuesto para medir la presión hidrostática. El elemento de presión se introduce en el fluido a una profundidad h. En la práctica real, el elemento de presión se puede girar a fin de demostrar que la presión solamente depende de la posición, pero es independiente de la dirección en la que se mide.

Seleccionamos uno de los fluidos cuyas densidades se recogen en la tabla y a continuación, se pulsa en el botón titulado Nuevo.

La última sustancia es el líquido manométrico, el mercurio.

Establecemos la profundidad deseada en el control titulado Profundidad. Medimos con el manómetro la presión, o también en la gráfica de la derecha, donde se representa la profundidad en el eje vertical y la presión en el eje horizontal.

Ejemplo:

Supongamos que el fluido es agua. Bajamos la cápsula de presión hasta una profundidad de 60 cm. La presión debida a la altura de fluido es

p=1000·9.8·0.6=5880 Pa

El manómetro marca 2.2 cm por ambas ramas, que corresponde a una presión de

p=13550·9.8·2·0.022=5843

Como el manómetro está abierto por el otro extremo, no nos mide la presión total (atmosférica más la altura de fluido) sino solamente la presión debida al fluido.

Como vemos en la gráfica de la derecha a la profundidad de 60 cm le corresponden algo menos de 106 000 Pa, que corresponden a la presión atmosférica (aproximadamente 100 000 Pa) más la presión debida a la altura de la columna de fluido (6000 Pa).

La gráfica de la derecha está trazada de forma no usual, ya que la presión (variable dependiente) debería estar en el eje vertical y la altura (variable independiente) en el eje horizontal. La gráfica por tanto, nos muestra la dependencia lineal de la presión p con la profundidad h.

p=p₀+ρgh

Fluido compresible

La presión p a una profundidad z, de un fluido cuya densidad ρ no cambia con la presión es

${\displaystyle p=p_0+\rho gz}$

p₀ es la presión atmosférica en z=0

Para un fluido cuya densidad cambia, la ecuación fundamental de la estática de fluidos se escribe en forma diferencial

${\displaystyle \frac{dp}{dz}=\rho g}$

Se define el módulo de compresibilidad (bulk modulus)

${\displaystyle B=\frac{-dp}{dV/V}}$

donde dV/V es el cambio (reducción) relativo de volumen de la muestra cuando se incrementa la presión en dp. Para una muestra de fluido de masa m=ρ/V

${\displaystyle \begin{array}{l}V=\frac{m}{\rho }\\ dV=-\frac{m}{{\rho }^2}d\rho \\ \frac{dV}{V}=-\frac{d\rho }{\rho }\\ B=\frac{-dp}{-\frac{d\rho }{\rho }}=\rho \frac{dp}{d\rho }\end{array}}$

Separamos variables para integrar

${\displaystyle \begin{array}{l}dp=B\frac{d\rho }{\rho }\\ {\displaystyle \underset{p_0}{\overset{p}{\int }}dp=B{\displaystyle \underset{{\rho }_0}{\overset{\rho }{\int }}\frac{d\rho }{\rho }}}\\ p=p_0+B\ln \left(\frac{\rho }{{\rho }_0}\right)\end{array}}$

Por otra parte, la ecuación fundamental, dp=ρg·dz

${\displaystyle \begin{array}{l}B\frac{d\rho }{\rho }=\rho gdz\\ {\displaystyle \underset{{\rho }_0}{\overset{\rho }{\int }}\frac{d\rho }{{\rho }^2}}=\frac{g}{B}{\displaystyle \underset{0}{\overset{z}{\int }}dz}\\ \frac{1}{{\rho }_0}-\frac{1}{\rho }=\frac{g}{B}z\end{array}}$

Combinando ambas ecuaciones, determinamos la presión p con la profundidad z

${\displaystyle p=p_0+B\ln \left(\frac{B}{B-{\rho }_{0}gz}\right)=p_0-B\ln \left(1-\frac{{\rho }_{0}g}{B}z\right)}$

Datos: p₀=1.01·10⁵ Pa, B=2.1·10⁹ Pa, ρ₀=1.025·10³ kg/m³, g=9.81 m/s², z=11.0·10³ m (fosa de las Marianas, 11 km de profundidad)

Obtenemos, p=1.1373·10⁸ Pa, en vez de p=1.1071·10⁸ Pa

Representamos el cociente p/p₀ con la profundidad z en km, cuando la densidad cambia y cuando permanece constante

p0=1.01e5; %presión atmosférica
B=2.1e9; %módulo de compresibilidad
rho_0=1.025e3; %densidad en z=0

hold on
fplot(@(z) 1-B*log(1-rho_0*9.81*z*1000/B)/p0,[0,11]); % z en km
fplot(@(z) 1+rho_0*9.91*z*1000/p0,[0,11]); 
hold off
grid on
xlabel('z (km)')
legend('compresible','incompresible','location', 'best')
ylabel('p/p_0')
title('Presión con la profundidad')

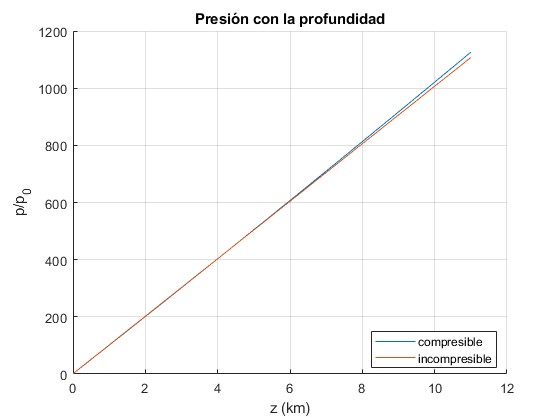
Solamente a grandes profundidades se aprecia la diferencia. En este cálculo se ha supuesto que la aceleración de la gravedad permanece constante, e igual a la de z=0, pero cambia con la profundidad

Fluido en rotación

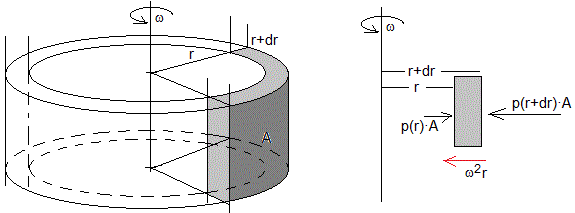
Sea un fluido de densidad ρ en rotación con velocidad angular constante ω. Consideremos un elemento de fluido comprendido entre r y r+dr, de área A, tal como se muestra en la figura, su masa es dm=ρ·A·dr

La presión del fluido a una distancia r, del eje de rotación es p(r) y la presión a una distancia r+dr es p(r+dr) ).

La fuerza sobre la cara interior del elemento es A·p(r), y la fuerza sobre la cara exterior del elemento de masa es A·p(r+dr) (véase la figura de la derecha).

El elemento de masa dm describe un circunferencia de radio r, la aceleración es ω²r dirigida hacia el centro. La segunda ley de Newton se escribe.

${\displaystyle \begin{array}{l}A·p(r)-A·p(r+dr)=-(\rho A·dr){\omega }^{2}r\\ \frac{dp}{dr}=\rho {\omega }^{2}r\end{array}}$

Integramos para obtener la diferencia de presión entre dos puntos del fluido en rotación situados a una distancia r₀ y r del eje.

${\displaystyle \begin{array}{l}{\displaystyle \underset{p(r_0)}{\overset{p(r)}{\int }}dp}={\displaystyle \underset{r_0}{\overset{r}{\int }}\rho {\omega }^{2}r·dr}\\ p(r)=p(r_0)+\frac{1}{2}\rho {\omega }^2\left(r^2-r_0^2\right)\end{array}}$

Si r₀=0 es el eje de rotación

${\displaystyle p(r)=\frac{1}{2}\rho {\omega }^2{r}^2}$

Que es la presión p del fluido en función de la distancia r al eje de rotación

Referencias

W. G. Rees. Physics by Example. 200 problems and solutions. Cambridge University Press, (1994), Problem 38, pp.84-85