Aplicaciones de la ecuación fundamental de la estática de fluidos

La ecuación fundamental de la estática de fluidos afirma que la presión depende únicamente de la profundidad. El principio de Pascal afirma que cualquier aumento de presión en la superficie de un fluido se transmite a cualquier punto del fluido. Una aplicación de este principio es la prensa hidráulica.

Otra aplicación de la ecuación fundamental de la estática de fluidos es la determinación de la densidad de un líquido no miscible con agua mediante un tubo en forma de U, comparando las diferentes alturas de las columnas de fluido sobre la superficie de separación.

Mediremos la presión del aire atrapado en un tubo cerrado por su extremo superior cuando se sumerje en un líquido

Finalmente, explicaremos una variante de la paradoja del vaso lleno de agua tapado con una cartulina rígida que se le da vuelta sin que el agua se derrame

La prensa hidráulica

Émbolos a la misma altura

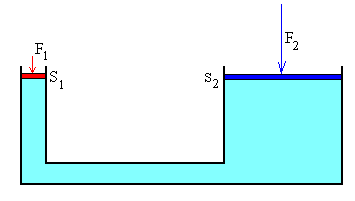
Se aplica una fuerza F₁ a un pequeño émbolo de área S₁. El resultado es una fuerza F₂ mucho más grande en el émbolo de área S₂. Debido a que la presión es la misma a la misma altura por ambos lados, se verifica que

$p = \frac{F_{1}}{S_{1}} = \frac{F_{2}}{S_{2}}$

Para mantener a la misma altura los dos émbolos, tenemos que poner un número de pesas sobre cada émbolo de modo que se cumpla la relación dada en el apartado anterior.

$\frac{n_{1} m g}{π r_{1}^{2}} = \frac{n_{2} m g}{π r_{2}^{2}} \frac{n_{1}}{r_{1}^{2}} = \frac{n_{2}}{r_{2}^{2}}$

Donde n₁ y n₂ es el número de pesas que se ponen en el émbolo izquierdo o derecho respectivamente, r₁ y r₂ son sus radios respectivos, m es la masa de cada pesa.

Ejemplo:

Si r₂ es el doble de r₁, el área S₂ del émbolo de la derecha es cuatro veces mayor que el área S₁ del émbolo de la izquierda. Para que los émbolos estén a la misma altura, a la derecha tenemos que poner cuatro veces más de pesas que a la izquierda.

r₂=2r₁ entonces S₂=4S₁, luego, n₂=4n₁

Émbolos a distinta altura

Vamos a determinar la altura de ambas columnas de fluido cuando se ponen n₁ pesas en el émbolo de la izquierda y n₂ pesas en el émbolo de la derecha.

Sean A y B dos puntos del fluido que están a la misma altura. El punto A una profundidad h₁ por debajo del émbolo de área S₁ y el B situado h₂ por debajo del émbolo de área S₂.

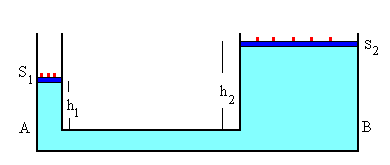
La presión en cada uno de dichos puntos es la suma de tres términos

La presión atmosférica
La presión debida a la columna de fluido
La presión debida a las pesas situadas sobre el émbolo

$\begin{array}{l} p_{A} = p_{0} + ρ g h_{1} + \frac{n_{1} m g}{π r_{1}^{2}} \\ p_{B} = p_{0} + ρ g h_{2} + \frac{n_{2} m g}{π r_{2}^{2}} \end{array}$

Para determinar h₁ y h₂ en función de los datos n₁ y n₂, precisamos de dos ecuaciones

La primera ecuación es p_A=p_B

La segunda ecuación, nos indica que el fluido incomprensible pasa de un recipiente al otro, pero el volumen V de fluido permanece invariable. Por ejemplo, si h₁ disminuye, h₂ aumenta. Como consecuencia, el fluido pasa del recipiente izquierdo al derecho, hasta que se establece de nuevo el equilibrio.

$π r_{1}^{2} h_{1} + π r_{2}^{2} h_{2} = (π r_{1}^{2} + π r_{2}^{2}) h_{0}$

Donde h₀ es la altura inicial de equilibrio.

Ejemplo 1:

Ponemos tres pesas en el émbolo de la izquierda, y ninguna pesa en el émbolo de la derecha, n₁=3, n₂=0. El émbolo izquierdo baja y sube el émbolo derecho.

Sea el radio del émbolo de la izquierda, r₁=5 cm=0.05 m
El radio del émbolo de la derecha, r₂=10 cm=0.1 m
La altura inicial de equilibrio, h₀=20 cm=0.2 m
La densidad del agua, ρ=1000 kg/m³
La masa m de cada una de las pesas es 250 g=0.25 kg.
La presión atmosférica p₀ se simplifica en la primera ecuación

Para hallar las alturas de equilibrio h₁ y h₂ tenemos que plantear el sistema de dos ecuaciones con dos incógnitas

Igualdad de presiones, p_A=p_B

$1000 g h_{1} + \frac{3 \cdot 0.25 \cdot g}{π {(0.05)}^{2}} = 1000 \cdot g \cdot h_{2}$

El agua pasa del recipiente izquierdo al recipiente derecho, pero el volumen total de fluido permanece invariable

$π {(0.05)}^{2} h_{1} + π {(0.1)}^{2} h_{2} = (π {(0.05)}^{2} + π {(0.1)}^{2}) 0.2$

La solución es h₁=0.124 m=12.4 cm y h₂=0.219 m=21.9 cm

Ejemplo 2:

Ponemos una pesa en el émbolo de la izquierda y 10 pesas en el émbolo de la derecha,n₁=1, n₂=10. El émbolo izquierdo baja y sube el émbolo derecho.

Sea el radio del émbolo de la izquierda, r₁=1 cm=0.01 m
El radio del émbolo de la derecha, r₂=6 cm=0.06 m

El sistema de dos ecuaciones con dos incógnitas

Igualdad de presiones p_A=p_B

$1000 g h_{1} + \frac{1 \cdot 0.25 \cdot g}{π {(0.01)}^{2}} = 1000 \cdot g \cdot h_{2} + \frac{10 \cdot 0.25 \cdot g}{π {(0.06)}^{2}}$

El agua pasa del recipiente izquierdo al recipiente derecho, pero el volumen total de fluido permanece invariable

$π {(0.01)}^{2} h_{1} + π {(0.06)}^{2} h_{2} = (π {(0.01)}^{2} + π {(0.06)}^{2}) 0.2$

La solución es h₁=-0.359 m=-35.9 cm y h₂=0.216 m=21.6 cm. Esta solución no es posible, por lo que el programa invita a modificar el número de pesas sobre ambos émbolos

Actividades

Se introduce

el radio del émbolo izquierdo, en el control titulado Radio izquierdo.
el radio del émbolo derecho, en el control titulado Radio derecho.
El número de pesas de 250 g sobre el émbolo izquierdo, en el control titulado Pesas izquierda
El número de pesas de 250 g sobre el émbolo derecho, en el control titulado Pesas derecha

Se pulsa el botón titulado Nuevo

El programa calcula las alturas h₁ y h₂. Si alguna de ellas es menor que cero, el programa invita a modificar el número de pesas sobre ambos émbolos

Radio izquierdo (cm): derecho:
Pesas izquierda: derecha:

Medida de la densidad relativa de un líquido

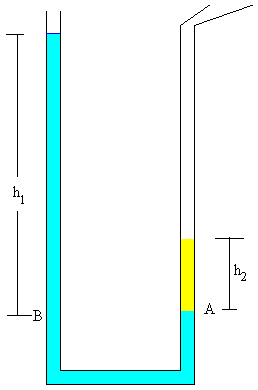
En esta experiencia aplicamos la ecuación fundamental de la estática de fluidos

Se comparan dos líquidos inmiscibles, el agua, cuya densidad es conocida (1.0 g/cm³).y un líquido de densidad desconocida.

Dado que A y B están a la misma altura sus presiones deben ser iguales:

La presión en A es debida a la presión atmosférica más la debida a la altura h₂ de la columna de fluido cuya densidad ρ₂ queremos determinar.

p_A=p₀+ρ₂gh₂

La presión en B es debida a la presión atmosférica más la debida a la altura h₁ de la columna de agua cuya densidad conocemos

p_B=p₀+ρ₁gh₁

Igualando las presiones en A y B, p_A=p_B, obtenemos

$\frac{ρ_{1}}{ρ_{2}} = \frac{h_{2}}{h_{1}}$

Las densidades de los dos líquidos no miscibles están en relación inversa a las alturas de sus columnas sobre la superficie de separación en el tubo en forma de U.

Actividades

Cuando se pulsa el botón titulado Nuevo, el programa interactivo genera un número aleatorio comprendido entre 0.5 y 4.5 que representa la densidad del líquido desconocido (en color amarillo).
Se vierte el líquido desconocido poco a poco por el extremo derecho que tiene forma de embudo, pulsando en el botón ►.
Paramos la ejecución del programa en cualquier momento, para realizar medidas pulsando en el botón pausa ||.
Nos acercarnos a una medida en la escala graduada pulsando varias veces en el botón paso a paso >|.
El programa se detiene cuando alguno de los indicadores de nivel se sale fuera de la escala graduada en cm.

Ejemplo

El líquido desconocido se representa en color amarillo y el agua en azul claro.

Medimos la altura de la columna de fluido desconocido sobre la superficie de separación (indicador de color rojo)
9-3.5=5.5 cm
Medimos la altura de la columna de agua sobre la superficie de separación
25-3.5=21.5 cm.

Despejamos la densidad ρ₂del líquido desconocido

$ρ_{2} = \frac{1.0 \cdot 21.5}{5.5} = 3.91 {g/cm}^{3}$

Presión del aire atrapado en un tubo que se sumerje en un fluido

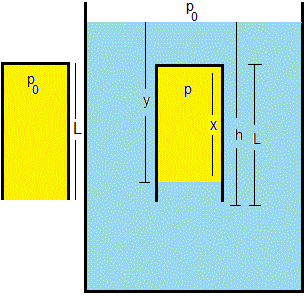
Consideremos un tubo de longitud L y sección S abierto por la parte inferior y cerrado por la parte superior. Lo introducimos en un fluido de densidad ρ conocida. A medida que sumergimos el tubo, el aire atrapado en su interior (en color amarillo) se comprime. Vamos a medir la presión de aire en el tubo

Sea p₀=101 300 N/m² la presión atmósférica. Sea h la posición del extremo inferior del tubo e y la posición de la superficie de separación entre el fluido y el aire atrapado en el tubo. Ambas longitudes se miden desde la superficie libre del fluido tal como se muestra en la figura

Supondremos que el aire experimenta una transformación isotérmica a la temperatura T del fluido contenido en el recipiente

Inicialmente n moles de aire ocupan un volumen SL a la temperatura T y a la presión atmosférica p₀. Suponiendo que el aire es un gas ideal,

p₀·SL=nRT

Cuando se introduce el tubo en el fluido, la presión en la superficie de separación entre el aire y el fluido es algo mayor, p=p₀+ρgy, por lo que el volumen S(L-(h-y)) se reduce si la temperatura se mantiene constante

p·S(L-(h-y))=nRT

Calculamos y a partir de las ecuaciones

$\begin{array}{l} p = p_{0} \frac{L}{L - h + y} \\ p = p_{0} + ρ g y \end{array}$

Obtenemos la ecuación de segundo grado

$\begin{array}{l} y^{2} + (L - h + \frac{p_{0}}{ρ g}) y - \frac{p_{0}}{ρ g} h = 0 \\ y = \frac{- (L - h + \frac{p_{0}}{ρ g}) + \sqrt{{(L - h + \frac{p_{0}}{ρ g})}^{2} + 4 \frac{p_{0}}{ρ g} h}}{2} \end{array}$

cuya raíz positiva es y.

El manómetro mide la diferencia de presión p-p₀=ρgy

Hemos calculado la diferencia de presión p-p₀ en términos de la densidad ρ del fluido, la presión atmosférica p₀, la longitud L del tubo y de las posiciones h del extremo del tubo e y de la superficie de separación que mediríamos con precisión mediante un catetómetro

Por otra parte, medimos la presión del gas p-p₀=ρ₁gH con un manómetro de mercurio, siendo H la diferencia de los niveles en ambas ramas del manómetro y ρ₁=13 550 kg/m³ la densidad del mercurio

Ejemplo

Densidad del fluido, agua, ρ=1000 kg/m³
Presión atmósférica, p₀=101 300 N/m²
Longitud del tubo, abierto por la parte inferior, L=40 cm
Se sumerge el tubo en el fluido hasta que la altura de su extremo inferior es, h=60 cm
La densidad del mercurio del manómetro es 13550 kg/m³

Con estos datos calculamos la posición y de la superficie de separación entre el aire y el fluido

>> rho=1000;
>> p0=101300;
>> h=0.6;
>> L=0.4;
>> b=L-h+p0/(rho*9.8);
>> c=-p0*h/(rho*9.8);
>> y=(-b+sqrt(b^2-4*c))/2
y =    0.5788

La diferencia de presión es p-p₀=ρgy=1000·9.8·0.579=5 672 Pa, lo que equivale a que la diferencia de alturas del manómetro sea 5 672/(9.8·13550)=0.0427 m=4.3 cm, que es lo que observamos en la simulación

Actividades

Se introduce

Se elige el fluido de densidad

Agua, ρ=1000 kg/m³
Aceite, ρ=900 kg/m³
Alcohol, ρ=790 kg/m³
Glicerina, ρ=1260 kg/m³

Se introduce la profundidad h en cm del extremo inferior abierto del tubo, en el control titulado Profundidad

Se pulsa el botón titulado Nuevo

El programa calcula la posición y de la superficie de separación entre el aire y el fluido. Mide la diferencia de presión p-p₀=ρgy mediante un manómetro de mercurio en la parte izquierda

Líquidos: Profundidad (cm):

Vaso lleno de agua

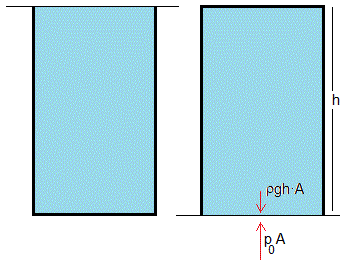
Una experiencia habitual es la de llenar un vaso de agua, cubrirlo con una cartulina rígida y darle la vuelta sin que se derrame agua

En YouTube se encuentran muchos vídeos, titulados 'Agua que no se cae', 'Dar la vuelta a un vaso sin que se derrame líquido', y otros

La fuerza que ejerce la presión atmosférica p₀A por debajo de la cartulina es superior al peso del agua ρgh·A. La sección del vaso es A.

p₀>ρgh

Para un vaso de h=10 cm de altura

101300>1000·9.8·0.1

Un experiento simple, fácil de explicar pero como veremos a continuación, tiene muchas facetas interesantes, cuando el vaso está parcialmente lleno de agua

El vaso de altura h está parcialmente lleno de agua hasta una altura d. Contiene aire a presión atmosférica p₀ que ocupa un volumen A(h-d)

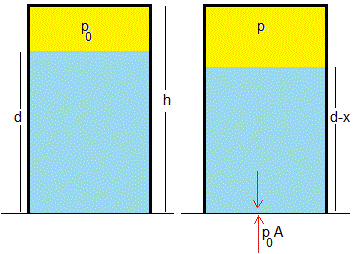
Pierde una pequeña cantidad de agua, aumentando el volumen de aire hasta A(h-d+x). Supondremos que el aire atrapado pasa de la situación inicial a la final mediante una proceso isotérmico

$p_{0} A (h - d) = p A (h - d + x)$

El equilibrio de fuerzas sobre la cartulina es

$p_{0} A = (p + ρ g (d - x)) A$

Eliminando la presión p en el sistema de dos ecuaciones

$\begin{array}{l} ρ g {(d - x)}^{2} - (ρ g h + p_{0}) (d - x) + p_{0} d = 0 \\ d - x = \frac{ρ g h + p_{0} - \sqrt{{(ρ g h + p_{0})}^{2} - 4 ρ g p_{0} d}}{2 ρ g} \end{array}$

Aproximación, x<<d

$\begin{array}{l} ρ g (d^{2} - 2 x d) - (ρ g h + p_{0}) (d - x) + p_{0} d \approx 0 \\ x \approx \frac{d (h - d)}{\frac{p_{0}}{ρ g} + h - 2 d} \end{array}$

Se ha despreciado x² frente a d²

Representamos el incremento x en función de d, para h=0.1 m, tomando la presión atmosférica p₀=101 300 Pa, la densidad del agua ρ=1000 kg/m³

h=0.1; %altura del vaso
p0=101300;  %Presión atmosférica en Pa
f=@(d) d.*(h-d)./(p0/9800+h-2*d);
g=@(d) d-(9800*h+p0-sqrt((9800*h+p0)^2-4*9800*p0*d))/(2*9800);
hold on
fplot(f,[0,h])
fplot(g,[0,h])
grid on
legend('Aprox.','Exacta')
xlabel('d')
ylabel('x')
title('Paradoja')

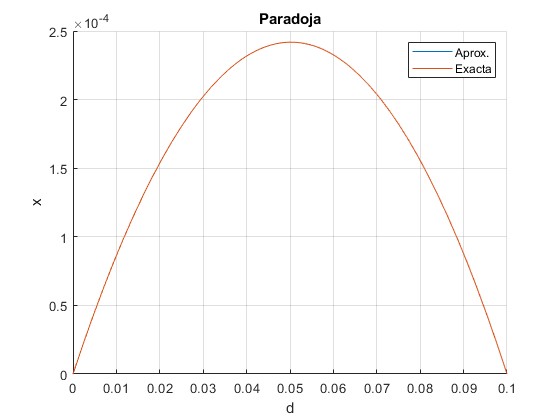
Observamos que no hay distinción entre los valores exactos y aproximados de x en función de d. El máximo de x se produce para h/2

Tensión superficial

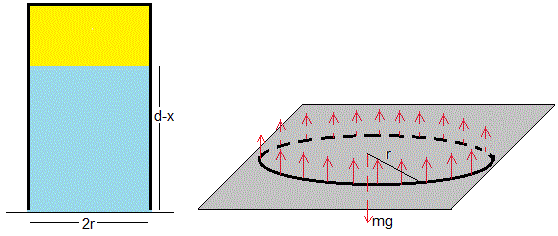
La fuerza que sustenta la cartulina proviene de la tensión superficial. La figura muestra la situación en la que el peso de la cartulina mg se compensa con la fuerza que ejerce la tensión superficial 2πr·γ, donde r es el radio del vaso. Supondremos un líquido que moja y su ángulo de contacto θ_c≈0

Referencias

Salvatore Ganci. A hydrostatic paradox revisited. Phys. Educ. 47 (2) 2012, pp. 152-154