Recipiente cilíndrico

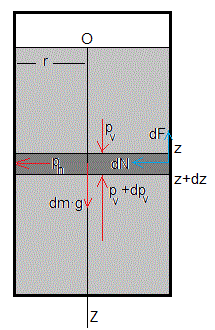
Sea un recipiente cilíndrico de radio r lleno de un material granular. Situamos el eje Z en el eje del recipiente y el origen O en la superficie del material granular.

Consideremos un elemento cilíndrico de dicho material de radio r situado entre z y z+dz. Las fuerzas sobre dicho elemento son

• El peso del elemento cilíndrico, ρ(πr²dz)g. ρ es la densidad del material granular

• La fuerza debida a la presión vertical en la cara inferior, (p_v+dp_v)·πr²

• La fuerza debida a la presión vertical en la cara superior p_v·πr²

• La fuerza de rozamiento dF entre los granos y la superficie lateral del elemento cilíndrico.

La fuerza que ejerce el material granular sobre la superficie lateral del elemento cilíndrico es p_h2πr·dz. Siendo p_h la presión horizontal. Dicha superficie ejerce una fuerza dN=p_h2πr·dz

de modo que la fuerza de rozamiento (máxima) es dF=μ·dN=μ·p_h2πr·dz. Siendo μ el coeficiente estático

En el equilibrio

${\displaystyle \begin{array}{l}\left(p_v+d{p}_v\right)\pi r^2=\left(\rho \pi r^{2}dz\right)g+p_v\pi r^2-\mu \left(p_h·2\pi r·dz\right)\\ \frac{d{p}_v}{dz}=\rho g-\frac{2\mu }{r}{p}_h\end{array}}$

Janssen relaciona las dos presiones p_h=k·p_v, 0≤k≤1. Obteniendo la ecuación diferencial en p_v (presión vertical)

${\displaystyle \frac{d{p}_v}{dz}=\rho g-\frac{2\mu k}{r}{p}_v}$

Integramos la ecuación diferencial, con la condición inicial para z=0, p_v=0

${\displaystyle \begin{array}{l}\frac{d{p}_v}{\rho g-\frac{2\mu k}{r}{p}_v}=dz\\ {\displaystyle \underset{0}{\overset{p_v}{\int }}\frac{d{p}_v}{\rho g-\frac{2\mu k}{r}{p}_v}={\displaystyle \underset{0}{\overset{z}{\int }}dz}}\\ {-\frac{r}{2\mu k}\ln \left(\rho g-\frac{2\mu k}{r}{p}_v\right)|}_0^{p_v}=z\\ \ln \left(\rho g-\frac{2\mu k}{r}{p}_v\right)-\ln \left(\rho g\right)=-\frac{2\mu k}{r}z\\ \frac{\rho g-\frac{2\mu k}{r}{p}_v}{\rho g}=\exp \left(-\frac{2\mu k}{r}z\right)\\ p_v=\frac{\rho gr}{2\mu k}\left(1-\exp \left(-\frac{2\mu k}{r}z\right)\right)\end{array}}$

fplot(@(z) 1-exp(-0.2*z), [0,30])
grid on
xlabel('z')
ylabel('p_v/p_{máx}')
title('Presión vertical de un material granular')

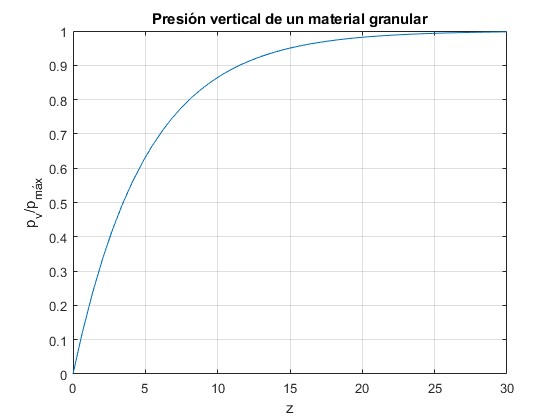
Se trata de una función que crece desde 0 hasta un valor límite constante,

${\displaystyle z>>\frac{r}{2\mu k},p_v\to p_{máx}=\frac{\rho gr}{2\mu k}}$

Cuando μ→0, (líquido incompresible), tenemos una indeterminación 0/0, que resolvemos aplicando la regla de L'Hôpital. Llamamos x=μk

${\displaystyle \begin{array}{l}\begin{array}{l}\underset{x\to 0}{\lim }\frac{\rho gr}{2x}\left(1-\exp \left(-\frac{2x}{r}z\right)\right)=\frac{\rho gr}{2}\underset{x\to 0}{\lim }\frac{1-\exp \left(-\frac{2x}{r}z\right)}{x}\hfill \\ \begin{array}{l}\underset{x\to 0}{\lim }\frac{f(x)}{g(x)}=\underset{x\to 0}{\lim }\frac{f\text{'}(x)}{g\text{'}(x)}\\ f(x)=1-\exp \left(-\frac{2x}{r}z\right),\frac{df(x)}{dx}=\frac{2}{r}z\exp \left(-\frac{2x}{r}z\right)\\ g(x)=x,\frac{dg(x)}{dx}=1\end{array}\hfill \end{array}\\ \frac{\rho gr}{2}\underset{x\to 0}{\lim }\frac{2}{r}z\exp \left(-\frac{2x}{r}z\right)=\rho gz\end{array}}$

La presión ρgz solamente depende de la altura z de fluido

Recipiente cónico

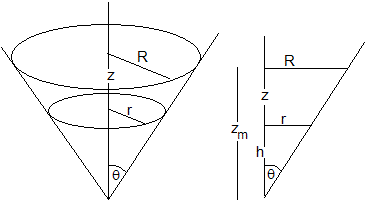
Sea R el radio de la superficie del material granular contenido en un recipiente cónico de ángulo 2θ.

El radio r del elemento cilíndrico, depende de la altura z

${\displaystyle \tan \theta =\frac{R}{z+h}=\frac{r}{h}}$

Eliminando h, obtenemos r=R-z·tanθ

La altura del material granular, z_m=R/tanθ, desde el vértice hasta la superficie de dicho material

La ecuación diferencial que nos proporciona la presión vertical p_v es

${\displaystyle \frac{d{p}_v}{dz}+\frac{2\mu k}{R-z\tan \theta }{p}_v=\rho g}$

El procedimiento para resolver esta ecuación diferencial se describe en la página titulada Ecuaciones diferenciales (I). Primero, resolvemos la ecuación diferencial homogénea

${\displaystyle \frac{d{p}_v}{dz}+\frac{2\mu k}{R-z\tan \theta }{p}_v=0}$

Separamos las variables

${\displaystyle \begin{array}{l}\frac{d{p}_v}{p_v}+2\mu k\frac{dz}{R-z\tan \theta }=0\\ {\displaystyle \int \frac{d{p}_v}{p_v}+2\mu k{\displaystyle \int \frac{dz}{R-z\tan \theta }}=c}\\ \ln p_v-\frac{2\mu k}{\tan \theta }\ln \left(R-z\tan \theta \right)=c\\ p_v=C(z){\left(R-z\tan \theta \right)}^{\frac{2\mu k}{\tan \theta }}\end{array}}$

Se introduce esta solución en la ecuación diferencial no homogénea

${\displaystyle \begin{array}{l}\frac{dC(z)}{dz}{\left(R-z\tan \theta \right)}^{\frac{2\mu k}{\tan \theta }}-\tan \theta \frac{2\mu k}{\tan \theta }{\left(R-z\tan \theta \right)}^{\frac{2\mu k}{\tan \theta }-1}C(z)+\frac{2\mu k}{R-z\tan \theta }C(z){\left(R-z\tan \theta \right)}^{\frac{2\mu k}{\tan \theta }}=\rho g\\ \frac{dC(z)}{dz}{\left(R-z\tan \theta \right)}^{\frac{2\mu k}{\tan \theta }}=\rho g\\ C(z)=\rho g{\displaystyle \int {\left(R-z\tan \theta \right)}^{-\frac{2\mu k}{\tan \theta }}dz+c}\\ C(z)=-\frac{\rho g}{\tan \theta }\frac{{\left(R-z\tan \theta \right)}^{-\frac{2\mu k}{\tan \theta }+1}}{-\frac{2\mu k}{\tan \theta }+1}+c\\ C(z)=\frac{\rho g}{2\mu k-\tan \theta }{\left(R-z\tan \theta \right)}^{-\frac{2\mu k}{\tan \theta }+1}+c\end{array}}$

La integral completa es

${\displaystyle \begin{array}{l}{p}_v=\left\{\frac{\rho g}{2\mu k-\tan \theta }{\left(R-z\tan \theta \right)}^{-\frac{2\mu k}{\tan \theta }+1}+c\right\}{\left(R-z\tan \theta \right)}^{\frac{2\mu k}{\tan \theta }}\\ p_v=\frac{\rho g}{2\mu k-\tan \theta }\left(R-z\tan \theta \right)+c{\left(R-z\tan \theta \right)}^{\frac{2\mu k}{\tan \theta }}\end{array}}$

La constante c de determina a partir de la condiciones iniciales, z=0, p_v=0

${\displaystyle \begin{array}{l}0=\frac{\rho g}{2\mu k-\tan \theta }R+c{R}^{\frac{2\mu k}{\tan \theta }}\\ c=-\frac{\rho g}{2\mu k-\tan \theta }{R}^{-\frac{2\mu k}{\tan \theta }+1}\end{array}}$

La expresión final de la presión p_v es

${\displaystyle \begin{array}{l}{p}_v=\frac{\rho g}{2\mu k-\tan \theta }\left(R-z\tan \theta \right)-\frac{\rho g}{2\mu k-\tan \theta }{R}^{-\frac{2\mu k}{\tan \theta }+1}{\left(R-z\tan \theta \right)}^{\frac{2\mu k}{\tan \theta }}\\ p_v=\frac{\rho gR}{2\mu k-\tan \theta }\left(1-\frac{z}{R}\tan \theta \right)\left\{1-{\left(1-\frac{z}{R}\tan \theta \right)}^{\frac{2\mu k}{\tan \theta }-1}\right\}\\ p_v=\frac{\rho g\frac{R}{\tan \theta }}{\frac{2\mu k}{\tan \theta }-1}\left\{1-\frac{z}{R}\tan \theta -{\left(1-\frac{z}{R}\tan \theta \right)}^{\frac{2\mu k}{\tan \theta }}\right\}\end{array}}$

Representamos p_v/(ρgz_m) en función de x=z/z_m, para varios valores del parámetro λ=2μk/tanθ

${\displaystyle \frac{p_v}{\rho g{z}_m}=\frac{1}{\lambda -1}\left\{1-\frac{z}{z_m}-{\left(1-\frac{z}{z_m}\right)}^{\lambda }\right\},z_m=\frac{R}{\tan \theta },\lambda =\frac{2\mu k}{\tan \theta }}$

hold on
for k=1./[1.6,1.1,0.6,0.1]
    f=@(x) (1-x-(1-x).^k)/(k-1);
     fplot(f, [0,1],'displayName',num2str(1/k))
     g=@(x) (1-x).^(k-1)-1/k;
     x_m=1-(1/k)^(1/(k-1));
     line([x_m,x_m],[0,f(x_m)],'lineStyle','--')
end
hold off
grid on
xlabel('z/z_m')
ylabel('p_v/(\rhogz_m)')
title('Presión vertical de un material granular')

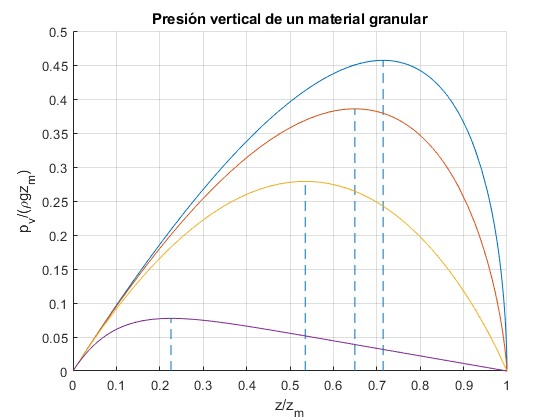
La presión p_v se anula en la superficie del material granular z=0 y en el vértice del cono Z_m. Presenta un máximo a una posición intermedia, x_máx

${\displaystyle \begin{array}{l}y=\frac{1}{\lambda -1}\left\{1-x-{\left(1-x\right)}^{\lambda }\right\},x=\frac{z}{z_m}\\ \frac{dy}{dx}=\frac{1}{\lambda -1}\left\{-1+\lambda {\left(1-x\right)}^{\lambda -1}\right\}=0\\ {\left(1-x\right)}^{\lambda -1}-\frac{1}{\lambda }=0\\ x_{máx}=1-{\left(\frac{1}{\lambda }\right)}^{\frac{1}{\lambda -1}}\end{array}}$

Referencias

Vladimir Ivchenko. Beyond Stevin’s law: the Janssen effect. Eur. J. Phys. 44 (2023) 025006