Masa del cuerpo celeste

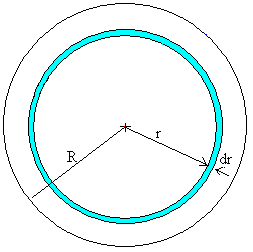
Supongamos un cuerpo celeste de masa M y radio R cuya densidad ρ(r) cambia con la distancia al centro.

Dividimos la esfera de radio R en capas esféricas de radio r y de espesor dr. La masa dm que contiene cada una de las capas es

${\displaystyle dm=\rho (r)\left(4\pi r^{2}dr\right)}$

La masa M(r) contenida en una esfera de radio r es

${\displaystyle M(r)=4\pi {\displaystyle \underset{0}{\overset{r}{\int }}\rho (r)r^{2}dr}}$

Cuando el límite superior es R tenemos la masa M del cuerpo celeste

Cuando la densidad es constante

${\displaystyle \rho =\frac{M}{\frac{4}{3}\pi R^3}}$

Presión en el centro

En una capa esférica de de radio r y de espesor dr, consideramos un elemento de volumen (en color rojo) de área dA. Las fuerzas sobre el elemento de masa dm=ρ·dA·dr son

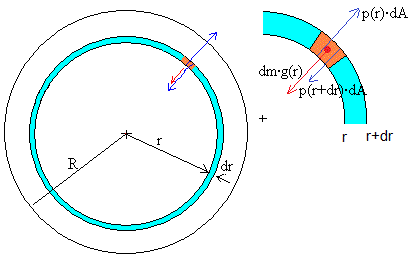
• La fuerza de atracción, dirigida hacia el centro de la Tierra dm·g(r). Donde g(r) es la aceleración de la gravedad a una distancia r del centro de la Tierra

• La fuerza que ejerce la presión p(r)·dA sobre la cara inferior del elemento de volumen

• La fuerza que ejerce la presión p(r+dr)·dA sobre la cara superior del elemento de volumen

En el equilibrio

${\displaystyle \begin{array}{l}\left(p\left(r+dr\right)-p(r)\right)dA=-g(r)\left(\rho (r)dA·dr\right)\\ dp=-g(r)\rho (r)·dr\end{array}}$

Obtenemos la ecuación

${\displaystyle \frac{dp}{dr}=-g(r)\rho (r)}$

La aceleración de la gravedad g(r) en un punto situado a una distancia r del centro, se debe (ley de Gauss) a la masa M(r) contenida en la esfera de radio r

${\displaystyle \begin{array}{l}g(r)=\frac{GM(r)}{r^2}\\ \frac{dp}{dr}=-\rho (r)\frac{GM(r)}{r^2}\end{array}}$

Densidad constante

Supongamos que la densidad ρ_c del cuerpo celeste es constante. La masa es

${\displaystyle M={\rho }_c\frac{4}{3}\pi R^3}$

Representamos la densidad ρ(r)/ρ_c en función de r/R

line([0,1],[1,1],'color','r')
grid on
ylim([0,1.1])
xlabel('r/R')
ylabel('\rho(r)/\rho_c')
title('Densidad')

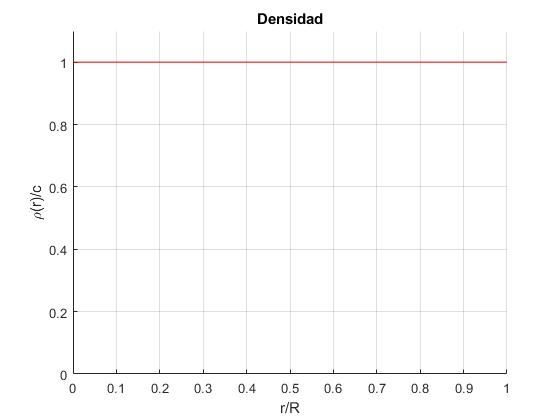
Calculamos la presión en el centro p_c para r=0

${\displaystyle \begin{array}{l}\frac{dp}{dr}=-\rho (r)\frac{GM(r)}{r^2}\\ \frac{dp}{dr}=-{\rho }_c\frac{G{\rho }_c\frac{4}{3}\pi r^3}{r^2}\\ {\displaystyle \underset{p_c}{\overset{0}{\int }}dp}=-\frac{4\pi }{3}G{\rho }_c^2{\displaystyle \underset{0}{\overset{R}{\int }}r·dr}\\ p_c=\frac{2\pi }{3}G{\rho }_c^2{R}^2\end{array}}$

La presión a una distancia r del centro

${\displaystyle \begin{array}{l}{\displaystyle \underset{p_c}{\overset{p}{\int }}dp}=-\frac{4\pi }{3}G{\rho }_c^2{\displaystyle \underset{0}{\overset{r}{\int }}r·dr}\\ p-p_c=-\frac{2\pi }{3}G{\rho }_c^2{r}^2\\ p=\frac{2\pi }{3}G{\rho }_c^2{R}^2\left(1-\frac{r^2}{R^2}\right)=p_c\left(1-\frac{r^2}{R^2}\right)\end{array}}$

fplot(@(x) 1-x.^2,[0,1],'color','b')
grid on
ylim([0,1.1])
xlabel('r/R')
ylabel('p(r)/p_c')
title('Presión')

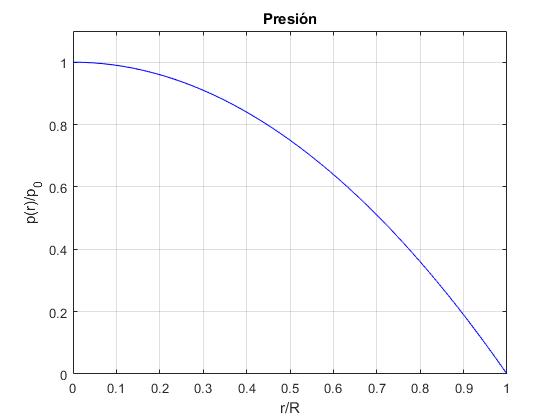
La densidad disminuye linealmente con la distancia al centro

Es un caso particular de la densidad que estudiaremos en el apartado siguiente con n=1

${\displaystyle \rho (r)={\rho }_c\left(1-\frac{r}{R}\right)}$

La masa del cuerpo celeste es

${\displaystyle \begin{array}{l}M(r)=4\pi {\displaystyle \underset{0}{\overset{r}{\int }}\rho (r)r^{2}dr}=4\pi {\rho }_c{\displaystyle \underset{0}{\overset{r}{\int }}\left(1-\frac{r}{R}\right)r^{2}dr=4\pi {\rho }_c\left(\frac{r^3}{3}-\frac{r^4}{4R}\right)}=\frac{4}{3}\pi {\rho }_c{r}^3\left(1-\frac{3}{4}\frac{r}{R}\right)\\ M=\frac{4}{3}\pi {\rho }_c{R}^3\left(1-\frac{3}{4}\right)=\frac{1}{3}\pi {\rho }_c{R}^3\end{array}}$

Calculamos la presión en el centro p_c para r=0

${\displaystyle \begin{array}{l}\frac{dp}{dr}=-\rho (r)\frac{GM(r)}{r^2}\\ \frac{dp}{dr}=-{\rho }_c\left(1-\frac{r}{R}\right)\frac{G\frac{4}{3}\pi {\rho }_c{r}^3\left(1-\frac{3}{4}\frac{r}{R}\right)}{r^2}=-\frac{4}{3}\pi G{\rho }_c^2\left(r-\frac{7}{4}\frac{r^2}{R}+\frac{3}{4}\frac{r^3}{R^2}\right)\\ {\displaystyle \underset{p_c}{\overset{0}{\int }}dp}=-\frac{4}{3}\pi G{\rho }_c^2{\displaystyle \underset{0}{\overset{R}{\int }}\left(r-\frac{7}{4}\frac{r^2}{R}+\frac{3}{4}\frac{r^3}{R^2}\right)dr}\\ p_c=\frac{4}{3}\pi G{\rho }_c^2\left(\frac{R^2}{2}-\frac{7}{12}\frac{R^3}{R}+\frac{3}{16}\frac{R^4}{R^2}\right)=\frac{5}{36}\pi G{\rho }_c^2{R}^2\end{array}}$

La presión a una distancia r del centro

${\displaystyle \begin{array}{l}{\displaystyle \underset{p_c}{\overset{p}{\int }}dp}=-\frac{4}{3}\pi G{\rho }_c^2{\displaystyle \underset{0}{\overset{r}{\int }}\left(r-\frac{7}{4}\frac{r^2}{R}+\frac{3}{4}\frac{r^3}{R^2}\right)dr}\\ p=p_c-\frac{2}{3}\pi G{\rho }_c^2{r}^2\left(1-\frac{7}{6}\frac{r}{R}+\frac{3}{8}\frac{r^2}{R^2}\right)\\ p=p_c\left(1-\frac{24}{5}\frac{r^2}{R^2}+\frac{28}{5}\frac{r^3}{R^3}-\frac{9}{5}\frac{r^4}{R^4}\right)\end{array}}$

La densidad es una función potencial

Supongamos que la densidad disminuye con la distancia r al centro de la forma

${\displaystyle \rho (r)={\rho }_c\left(1-\frac{r^n}{R^n}\right)}$

Representamos la densidad ρ/ρ_c en función del cociente r/R para n= 1, 3, 5, 7, 9. El caso, n=1, es la densidad lineal estudiada en el apartado anterior

hold on
for n=1:2:9
    fplot(@(x) 1-x.^n, [0,1], 'displayName',num2str(n))
end
grid on
xlabel('r/R')
legend('-DynamicLegend','location','best')
ylabel('\rho/\rho_c')
title('Densidad')

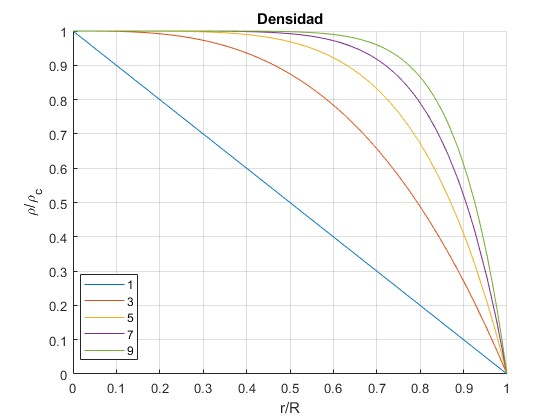
La masa del cuerpo celeste es

${\displaystyle \begin{array}{l}M(r)=4\pi {\displaystyle \underset{0}{\overset{r}{\int }}\rho (r)r^{2}dr}=4\pi {\rho }_c{\displaystyle \underset{0}{\overset{r}{\int }}\left(1-\frac{r^n}{R^n}\right)r^{2}dr=4\pi {\rho }_c\left(\frac{r^3}{3}-\frac{r^{n+3}}{\left(n+3\right)R^n}\right)=\frac{4}{3}}\pi {\rho }_c{r}^3\left(1-\frac{3}{n+3}\frac{r^n}{R^n}\right)\\ M=\pi {\rho }_c{R}^3\left(1-\frac{3}{n+3}\right)\end{array}}$

Calculamos la presión en el centro p_c para r=0

${\displaystyle \begin{array}{l}\frac{dp}{dr}=-\rho (r)\frac{GM(r)}{r^2}\\ \frac{dp}{dr}=-{\rho }_c\left(1-\frac{r^n}{R^n}\right)\frac{G\frac{4}{3}\pi {\rho }_c{r}^3\left(1-\frac{3}{n+3}\frac{r^n}{R^n}\right)}{r^2}=-\frac{4}{3}\pi G{\rho }_c^2\left(r-\frac{n+6}{n+3}\frac{r^{n+1}}{R^n}+\frac{3}{n+3}\frac{r^{2n+1}}{R^{2n}}\right)\\ {\displaystyle \underset{p_c}{\overset{0}{\int }}dp}=-\frac{4}{3}\pi G{\rho }_c^2{\displaystyle \underset{0}{\overset{R}{\int }}\left(r-\frac{n+6}{n+3}\frac{r^{n+1}}{R^n}+\frac{3}{n+3}\frac{r^{2n+1}}{R^{2n}}\right)dr}\\ p_c=\frac{4}{3}\pi G{\rho }_c^2\left(\frac{R^2}{2}-\frac{n+6}{(n+3)(n+2)}\frac{R^{n+2}}{R^n}+\frac{3}{2(n+3)(n+1)}\frac{R^{2(n+1)}}{R^{2n}}\right)=\frac{2}{3}\pi G{\rho }_c^2{R}^2\left(1-\frac{2(n+6)}{(n+3)(n+2)}+\frac{3}{(n+3)(n+1)}\right)\\ p_c=\frac{2}{3}\pi G{\rho }_c^2{R}^2\frac{n^2\left(n+4\right)}{(n+3)(n+2)(n+1)}\end{array}}$

La presión a una distancia r del centro

${\displaystyle \begin{array}{l}{\displaystyle \underset{p_c}{\overset{p}{\int }}dp}=-\frac{4}{3}\pi G{\rho }_c^2{\displaystyle \underset{0}{\overset{r}{\int }}\left(r-\frac{n+6}{n+3}\frac{r^{n+1}}{R^n}+\frac{3}{n+3}\frac{r^{2n+1}}{R^{2n}}\right)dr}\\ p=p_c-\frac{2}{3}\pi G{\rho }_c^2{r}^2\left(1-\frac{2(n+6)}{(n+3)(n+2)}\frac{r^n}{R^n}+\frac{3}{(n+3)(n+1)}\frac{r^{2n}}{R^{2n}}\right)\\ p=p_c\left(1-\frac{(n+3)(n+2)(n+1)}{n^2\left(n+4\right)}\frac{r^2}{R^2}+\frac{2(n+6)(n+1)}{n^2\left(n+4\right)}\frac{r^{n+2}}{R^{n+2}}-\frac{3(n+2)}{n^2\left(n+4\right)}\frac{r^{2n+2}}{R^{2n+2}}\right)\end{array}}$

Comprobamos que para n=1, obtenemos el resultado del apartado anterior

Representamos la presión p/p_c en función del cociente r/R para n= 1, 3, 5, 7, 9. El caso, n=1, (primera curva de color azul) corresponde a la densidad lineal estudiada en el apartado anterior

hold on
for n=1:2:9
    f=@(x) 1-(n+3)*(n+2)*(n+1)*x.^2/(n^2*(n+4))+2*(n+6)*(n+1)*x.^(n+2)/(n^2*(n+4))
-3*(n+2)*x.^(2*n+2)/(n^2*(n+4));
    fplot(f, [0,1], 'displayName',num2str(n))
end
grid on
xlabel('r/R')
legend('-DynamicLegend','location','best')
ylabel('p/p_c')
title('Presión')

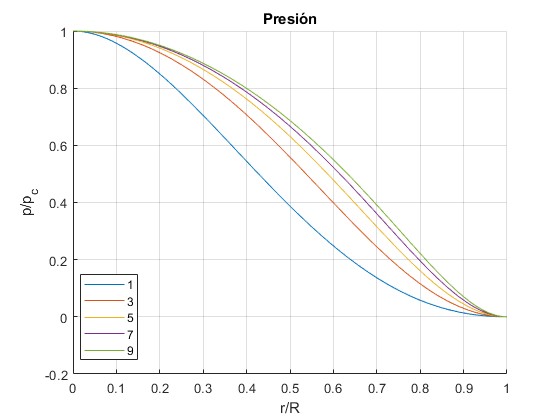
La densidad es una función exponencial decreciente

La densidad ρ(r) es

${\displaystyle \rho (r)={\rho }_c\left(1-\frac{r}{3R}\right)e^{-\frac{r}{R}}}$

Representamos la densidad ρ(r)/ρ_c en función de r/R

fplot(@(x) (1-x/3).*exp(-x),[0,1])
grid on
ylim([0,1.1])
xlabel('r/R')
ylabel('\rho(r)/\rho_c')
title('Densidad')

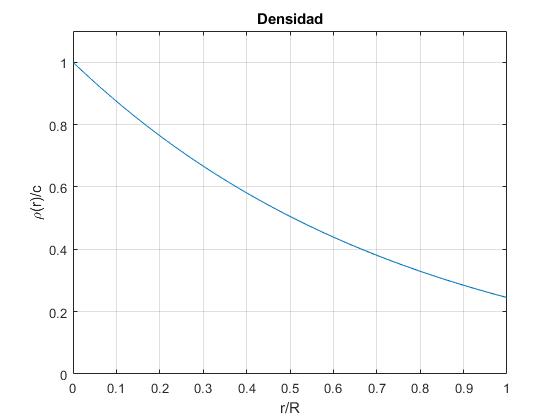
La masa de gas contenida en la esfera de radio r es

${\displaystyle \begin{array}{l}M(r)=4\pi {\displaystyle \underset{0}{\overset{r}{\int }}\rho (r)r^2·dr}=4\pi {\displaystyle \underset{0}{\overset{r}{\int }}{\rho }_c\left(1-\frac{r}{3R}\right)e^{-\frac{r}{R}}{r}^2·dr}=\\ 4\pi {\rho }_c\left\{{\displaystyle \underset{0}{\overset{r}{\int }}{r}^2{e}^{-\frac{r}{R}}·dr}-\frac{1}{3R}{\displaystyle \underset{0}{\overset{r}{\int }}{r}^3{e}^{-\frac{r}{R}}·dr}\right\}\end{array}}$

Integrando por partes

${\displaystyle {\displaystyle \int r^3{e}^{-\frac{r}{R}}·dr}=-R{r}^3{e}^{-\frac{r}{R}}+3R{\displaystyle \int r^2{e}^{-\frac{r}{R}}·dr}}$

El resultado es

${\displaystyle M(r)=\frac{4}{3}\pi {\rho }_c{r}^3{e}^{-\frac{r}{R}}}$

La ecuación diferencial se escribe

${\displaystyle \frac{dp}{dr}=-G\frac{M(r)·\rho (r)}{r^2}=-\frac{4}{3}\pi G{\rho }_c^{2}r\left(1-\frac{r}{3R}\right)e^{-2\frac{r}{R}}}$

Integramos entre 0 y r

${\displaystyle p-p_c=-\frac{4}{3}\pi G{\rho }_c^2\left\{{\displaystyle \underset{0}{\overset{r}{\int }}r{e}^{-2\frac{r}{R}}}dr-\frac{1}{3R}{\displaystyle \underset{0}{\overset{r}{\int }}{r}^2{e}^{-2\frac{r}{R}}}dr\right\}}$

Integrando por partes

${\displaystyle \begin{array}{l}{\displaystyle \int r^2{e}^{-2\frac{r}{R}}·dr}=-\frac{R}{2}{r}^2{e}^{-2\frac{r}{R}}+R{\displaystyle \int r{e}^{-2\frac{r}{R}}·dr}\\ {\displaystyle \int r{e}^{-2\frac{r}{R}}·dr}=-\frac{R}{2}r{e}^{-2\frac{r}{R}}-\frac{R^2}{4}{e}^{-2\frac{r}{R}}\end{array}}$

El resultado es

${\displaystyle p-p_c=-\frac{4}{3}\pi G{\rho }_c^2{R}^2\frac{1}{3}\left\{\frac{1}{2}+\left(\frac{1}{2}\frac{r^2}{R^2}-\frac{r}{R}-\frac{1}{2}\right)e^{-2\frac{r}{R}}\right\}}$

Donde p_c es la presión en el centro de la esfera que determinamos sabiendo que p(R)=0

${\displaystyle \begin{array}{l}p(R)-p_c=-\frac{4}{3}\pi G{\rho }_c^2{R}^2\frac{1}{3}\left\{\frac{1}{2}-\frac{1}{e^2}\right\}\\ p_c=\frac{4}{9}\pi G{\rho }_c^2{R}^2\left\{\frac{1}{2}-\frac{1}{e^2}\right\}\end{array}}$

La presión p en función de la distancia radial r es

${\displaystyle p=\frac{2}{9}\pi G{\rho }_c^2{R}^2\left\{\left(1+2\frac{r}{R}-\frac{r^2}{R^2}\right)e^{-2\frac{r}{R}}-\frac{1}{e^2}\right\}}$

Representamos p(r)/p_c en función de r/R

${\displaystyle \frac{p}{p_c}=\frac{\left(1+2\frac{r}{R}-\frac{r^2}{R^2}\right)e^{2-2\frac{r}{R}}-2}{e^2-2}}$

f=@(x) ((1+2*x-x.^2).*exp(2-2*x)-2)/(exp(2)-2); 
fplot(f,[0,1])
grid on
ylim([0,1.1])
xlabel('r/R')
ylabel('p(r)/p_c')
title('Presión')

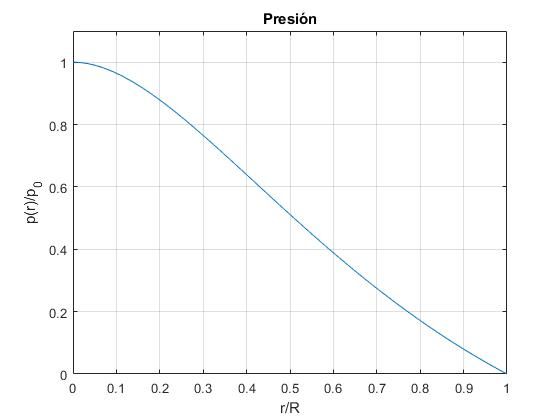
Otra condición de contorno sería que la presión en el infinito fuese nula p(∞)=0

${\displaystyle \begin{array}{l}p(\infty )-p_c=-\frac{4}{3}\pi G{\rho }_c^2{R}^2\frac{1}{3}\frac{1}{2}\\ p_c=\frac{2}{9}\pi G{\rho }_c^2{R}^2\end{array}}$

La presión p en función de la distancia radial r es

${\displaystyle p=\frac{2}{9}\pi G{\rho }_c^2{R}^2\left(1+2\frac{r}{R}-\frac{r^2}{R^2}\right)e^{-2\frac{r}{R}}}$

Representamos p(r)/p_c en función de r/R

${\displaystyle \frac{p}{p_c}=\left(1+2\frac{r}{R}-\frac{r^2}{R^2}\right)e^{-2\frac{r}{R}}}$

f=@(x) (1+2*x-x.^2).*exp(-2*x); 
fplot(f,[0,3])
grid on
ylim([0,1.1])
xlabel('r/R')
ylabel('p(r)/p_c')
title('Presión')

La densidad es una función gausiana

La densidad ρ(r) es

${\displaystyle \rho (r)={\rho }_c\left(1-\frac{2}{3}\frac{r^2}{R^2}\right)e^{-\frac{r^2}{R^2}}}$

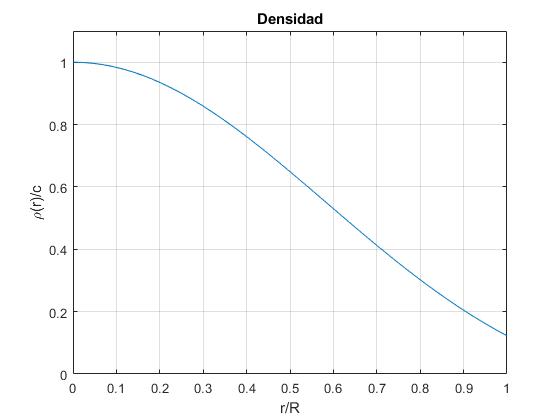
Representamos la densidad ρ(r)/ρ_c en función de r/R

fplot(@(x) (1-2*x.^2/3).*exp(-x.^2),[0,1])
grid on
ylim([0,1.1])
xlabel('r/R')
ylabel('\rho(r)/\rho_c')
title('Densidad')

La masa de gas contenida en la esfera de radio r es

${\displaystyle \begin{array}{l}M(r)=4\pi {\displaystyle \underset{0}{\overset{r}{\int }}\rho (r)r^2·dr}=4\pi {\displaystyle \underset{0}{\overset{r}{\int }}{\rho }_c\left(1-\frac{2}{3}\frac{r^2}{R^2}\right)e^{-\frac{r^2}{R^2}}{r}^2·dr}=\\ 4\pi {\rho }_c\left\{{\displaystyle \underset{0}{\overset{r}{\int }}{r}^2{e}^{-\frac{r^2}{R^2}}·dr}-\frac{2}{3}\frac{1}{R^2}{\displaystyle \underset{0}{\overset{r}{\int }}{r}^4{e}^{-\frac{r^2}{R^2}}·dr}\right\}\end{array}}$

Integrando por partes

${\displaystyle {\displaystyle \int r^4{e}^{\frac{-r^2}{R^2}}dr=-\frac{R^2}{2}{r}^3}{e}^{\frac{-r^2}{R^2}}+\frac{3}{2}{R}^2{\displaystyle \int r^2{e}^{\frac{-r^2}{R^2}}dr}}$

El resultado es

${\displaystyle M(r)=\frac{4}{3}\pi {\rho }_c{r}^3{e}^{-\frac{r^2}{R^2}}}$

La ecuación diferencial se escribe

${\displaystyle \frac{dp}{dr}=-G\frac{M(r)·\rho (r)}{r^2}=-\frac{4}{3}\pi G{\rho }_c^{2}r\left(1-\frac{2}{3}\frac{r^2}{R^2}\right)e^{-2\frac{r^2}{R^2}}}$

Integramos entre 0 y r

${\displaystyle p-p_c=-\frac{4}{3}\pi G{\rho }_c^2\left\{{\displaystyle \underset{0}{\overset{r}{\int }}r{e}^{-2\frac{r^2}{R^2}}}dr-\frac{2}{3R^2}{\displaystyle \underset{0}{\overset{r}{\int }}{r}^3{e}^{-2\frac{r^2}{R^2}}}dr\right\}}$

Tenemos una integral inmediata y otra por partes

${\displaystyle \begin{array}{l}{\displaystyle \int r{e}^{-2\frac{r^2}{R^2}}·dr}=-\frac{R^2}{4}{e}^{-2\frac{r^2}{R^2}}\\ {\displaystyle \int r^3{e}^{-2\frac{r^2}{R^2}}·dr}=-\frac{R^2}{4}{r}^2{e}^{-2\frac{r^2}{R^2}}-\frac{R^4}{8}{e}^{-2\frac{r^2}{R^2}}\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}p-p_c={-\frac{4}{3}\pi G{\rho }_c^2\frac{1}{6}\left(-R^2+r^2\right)e^{-2\frac{r^2}{R^2}}|}_0^r=\\ -\frac{2}{9}\pi G{\rho }_c^2\left\{\left(-R^2+r^2\right)e^{-2\frac{r^2}{R^2}}+R^2\right\}\end{array}}$

Donde p_c es la presión en el centro de la esfera que determinamos sabiendo que p(R)=0

${\displaystyle \begin{array}{l}p(R)-p_c=-\frac{2}{9}\pi G{\rho }_c^2{R}^2\\ p_c=\frac{2}{9}\pi G{\rho }_c^2{R}^2\end{array}}$

La presión p en función de la distancia radial r es

${\displaystyle p=\frac{2}{9}\pi G{\rho }_c^2{R}^2\left(1-\frac{r^2}{R^2}\right)e^{-2\frac{r^2}{R^2}}}$

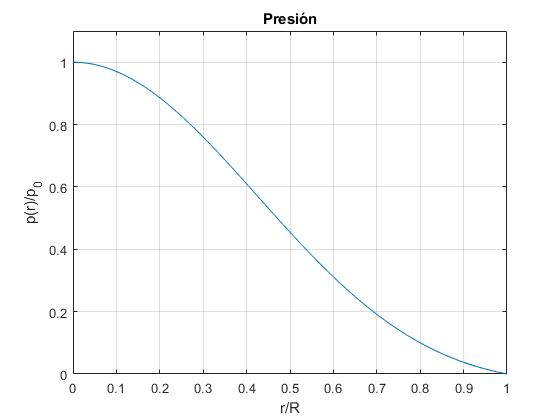
Representamos p(r)/p_c en función de r/R

${\displaystyle \frac{p}{p_c}=\left(1-\frac{r^2}{R^2}\right)e^{-2\frac{r^2}{R^2}}}$

f=@(x) (1-x.^2).*exp(-2*x.^2); 
fplot(f,[0,1])
grid on
ylim([0,1.1])
xlabel('r/R')
ylabel('p(r)/p_c')
title('Presión')

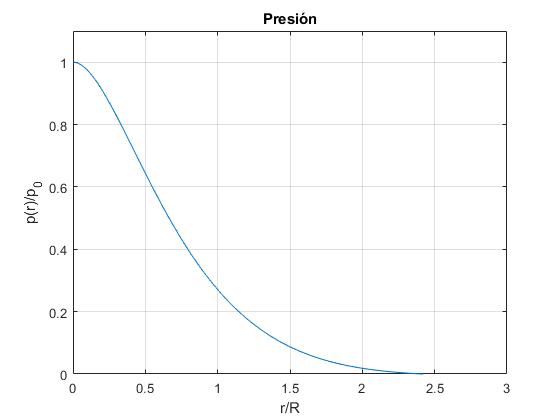
Otra condición de contorno sería que la presión en el infinito fuese nula p(∞)=0

${\displaystyle \begin{array}{l}p(\infty )-p_c=-\frac{2}{9}\pi G{\rho }_c^2{R}^2\\ p_c=\frac{2}{9}\pi G{\rho }_c^2{R}^2\end{array}}$

La presión p en función de la distancia radial r es

${\displaystyle p=\frac{2}{9}\pi G{\rho }_c^2{R}^2\left(1-\frac{r^2}{R^2}\right)e^{-2\frac{r^2}{R^2}}}$

Se obtiene el mismo resultado

Modelo para el gradiente de presión dp/dr

En el tercer artículo citado en las referencias, se propone un modelo para el gradiente de presión que represente de forma analítica sencilla la estructura del interior del Sol.

${\displaystyle \frac{dp}{dr}=-\frac{4\pi }{3}G{\rho }_c^{2}r\exp \left(-\frac{r^2}{a^2}\right)}$

donde a es un parámetro de ajuste. El gradiente de presión tiene la forma de la función

${\displaystyle y=-kx\exp \left(-x^2\right),x=\frac{r}{a}}$

La función tiene un extremo, que calculamos derivando con respecto de x,

${\displaystyle \begin{array}{l}\frac{dy}{dx}=-k\exp \left(-x^2\right)+2x^{2}k\exp \left(-x^2\right)=0\\ x=\frac{1}{\sqrt{2}}\end{array}}$

para $r=\frac{a}{\sqrt{2}}$ el gradiente de presión presenta un mínimo.

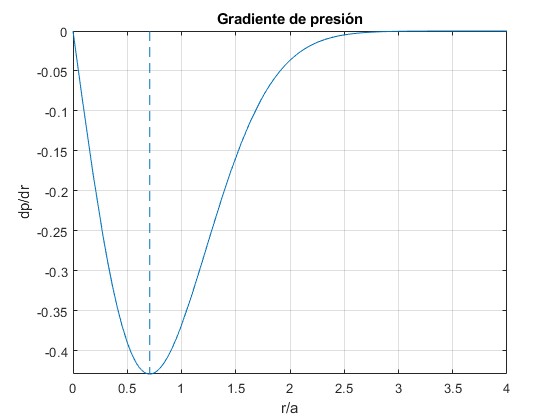
Representamos el gradiente de presión dp/dr en función de r/a

f=@(x) -x.*exp(-x.^2);
fplot(f, [0,4])
line([1/sqrt(2), 1/sqrt(2)],[0,f(1/sqrt(2))], 'lineStyle','--')
grid on
xlabel('r/a')
ylabel('dp/dr')
title('Gradiente de presión')

La presión en el centro, r=0

${\displaystyle \begin{array}{l}{\displaystyle \underset{p_c}{\overset{0}{\int }}dp}=-\frac{4\pi }{3}G{\rho }_c^2{\displaystyle \underset{0}{\overset{R}{\int }}r\exp \left(-\frac{r^2}{a^2}\right)dr}\\ p_c=\frac{2\pi }{3}G{\rho }_c^2{a}^2\left(1-\exp \left(-\frac{R^2}{a^2}\right)\right)\end{array}}$

El segundo término podría ser despreciable frente a la unidad

${\displaystyle p_c\approx \frac{2\pi }{3}G{\rho }_c^2{a}^2}$

Hemos obtenido una expresión similar cuando la densidad es constante, R el radio del cuerpo celeste, en vez del parámetro a

La presión para cualquier valor de r es

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{p}{\int }}dp}=-\frac{4\pi }{3}G{\rho }_c^2{\displaystyle \underset{R}{\overset{r}{\int }}r\exp \left(-\frac{r^2}{a^2}\right)dr}\\ p(r)=\frac{2\pi }{3}G{\rho }_c^2{a}^2\left(\exp \left(-\frac{r^2}{a^2}\right)-\exp \left(-\frac{R^2}{a^2}\right)\right)\end{array}}$

Dado el gradiente de presión dp/dr calculamos la masa del cuerpo celeste

Partimos de las relaciones

${\displaystyle \begin{array}{l}dM(r)=4\pi r^2\rho (r)·dr\\ \frac{dp}{dr}=-\rho (r)\frac{GM(r)}{r^2}\\ \frac{dp}{dr}=-\frac{4\pi }{3}G{\rho }_c^{2}r\exp \left(-\frac{r^2}{a^2}\right)\end{array}}$

Llegamos a la masa M(r)

${\displaystyle \begin{array}{l}\frac{dM(r)}{dr}M(r)=4\pi r^2\rho (r)M(r)=4\pi r^2\left(-\frac{r^2}{G}\frac{dp}{dr}\right)=4\pi r^4\frac{4\pi }{3}{\rho }_c^{2}r\exp \left(-\frac{r^2}{a^2}\right)\\ \frac{1}{2}\frac{d{M}^2(r)}{dr}=\frac{16{\pi }^2}{3}{\rho }_c^2{r}^5\exp \left(-\frac{r^2}{a^2}\right)\\ M^2(r)=\frac{32{\pi }^2}{3}{\rho }_c^2{\displaystyle \underset{0}{\overset{r}{\int }}{r}^5\exp \left(-\frac{r^2}{a^2}\right)dr}=\frac{32{\pi }^2}{3}{\rho }_c^2{a}^6{\displaystyle \underset{0}{\overset{x}{\int }}{x}^5\exp \left(-x^2\right)dx},x=\frac{r}{a}\end{array}}$

Hacemos el cambio de variable y=x², dy=2x·dx. Integramos dos veces por partes

${\displaystyle \begin{array}{l}{\displaystyle \int x^5\exp \left(-x^2\right)dx}=\frac{1}{2}{\displaystyle \int y^2{e}^{-y}dy},\{\begin{array}{l}u=y^2,du=2ydy\\ dv=e^{-y}dy,v=-e^{-y}\end{array}\\ \frac{1}{2}{\displaystyle \int y^2{e}^{-y}dy}=\frac{1}{2}\left\{-y^2{e}^{-y}+2{\displaystyle \int y{e}^{-y}dy}\right\},\{\begin{array}{l}u=y,du=dy\\ dv=e^{-y}dy,v=-e^{-y}\end{array}\\ =\frac{1}{2}\left\{-y^2{e}^{-y}+2\left\{-y{e}^{-y}+{\displaystyle \int e^{-y}dy}\right\}\right\}=\frac{1}{2}\left\{-y^2{e}^{-y}+2\left\{-y{e}^{-y}-e^{-y}\right\}\right\}=\\ -\frac{e^{-x^2}}{2}\left(x^4+2x^2+2\right)\end{array}}$

La masa del cuerpo celeste es M=M(R)

${\displaystyle \begin{array}{l}M=\frac{4\pi }{3}{\rho }_c{a}^3\sqrt{\left(6-3\exp \left(-\frac{R^2}{a^2}\right)\left(\frac{R^4}{a^4}+2\frac{R^2}{a^2}+2\right)\right)}\approx \frac{4\pi }{3}{\rho }_c{a}^3\sqrt{6}\\ {\rho }_c\approx \frac{M}{\frac{4\pi }{3}{a}^3\sqrt{6}}\end{array}}$

Conocida la masa M(r) calculamos la densidad ρ(r)

Partimos de las relaciones

${\displaystyle \begin{array}{l}\frac{dp}{dr}=-\rho (r)\frac{GM(r)}{r^2}\\ \frac{dp}{dr}=-\frac{4\pi }{3}G{\rho }_c^{2}r\exp \left(-\frac{r^2}{a^2}\right)\\ M(r)=\frac{4\pi }{3}{\rho }_c{a}^3\sqrt{\left(6-3\exp \left(-\frac{r^2}{a^2}\right)\left(\frac{r^4}{a^4}+2\frac{r^2}{a^2}+2\right)\right)}\end{array}}$

Despejamos la densidad ρ(r)

${\displaystyle \begin{array}{l}\rho (r)={\rho }_c\frac{r^3\exp \left(-\frac{r^2}{a^2}\right)}{a^3\sqrt{\left(6-3\exp \left(-\frac{r^2}{a^2}\right)\left(\frac{r^4}{a^4}+2\frac{r^2}{a^2}+2\right)\right)}}\\ \rho (r)={\rho }_c\frac{x^3\exp \left(-x^2\right)}{\sqrt{\left(6-3\exp \left(-x^2\right)\left(x^4+2x^2+2\right)\right)}},x=\frac{r}{a}\end{array}}$

Representamos la densidad ρ/ρ_c en función de x=r/a

f=@(x) x.^3.*exp(-x.^2)./sqrt(6-3*exp(-x.^2).*(x.^4+2*x.^2+2));
fplot(f, [0,5])
grid on
xlabel('r/a')
ylabel('\rho/\rho_c')
title('Densidad')

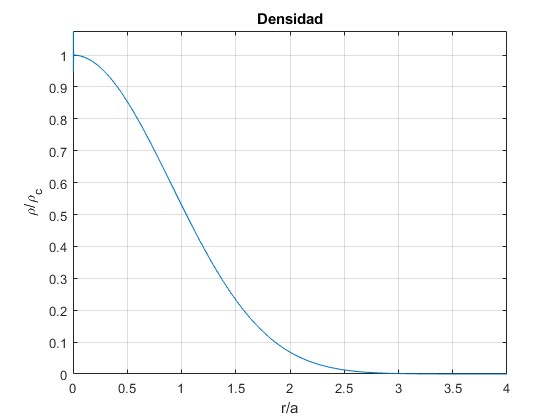
Cuando x→0, es pequeño

>> syms x;
>> taylor(exp(-x^2), x,0,'order',7)
ans =- x^6/6 + x^4/2 - x^2 + 1

${\displaystyle \exp \left(-x^2\right)\approx 1-x^2+\frac{x^4}{2}-\frac{x^6}{6}}$

El denominador

${\displaystyle \sqrt{\left(6-3\exp \left(-x^2\right)\left(x^4+2x^2+2\right)\right)}\approx \sqrt{\left(6-3\left(1-x^2+\frac{x^4}{2}-\frac{x^6}{6}\right)\left(x^4+2x^2+2\right)\right)}=x^3\sqrt{1-\frac{x^2}{2}+\frac{x^4}{2}}}$

El cociente

${\displaystyle \underset{x\to 0}{\lim }\frac{x^3\exp \left(-x^2\right)}{\sqrt{\left(6-3\exp \left(-x^2\right)\left(x^4+2x^2+2\right)\right)}}=\underset{x\to 0}{\lim }\frac{\exp \left(-x^2\right)}{\sqrt{1-\frac{x^2}{2}+\frac{x^4}{2}}}=1}$

tal como se aprecia en la representación gráfica

Cuando x→∞, es grande

${\displaystyle \frac{x^3\exp \left(-x^2\right)}{\sqrt{\left(6-3\exp \left(-x^2\right)\left(x^4+2x^2+2\right)\right)}}\approx \frac{x^3\exp \left(-x^2\right)}{\sqrt{6}}}$

Referencias

Andrei Smirnov, Ricardo Max Menezes Oliveira. Esferas de gás em estado de equilíbrio sob ação da gravitação própria. Revista Brasileira de Ensino de Física, v. 37, n. 1, 1308 (2015) https://www.scielo.br/j/rbef/i/2015.v37n1/

Mohammed Abobaker. Equilibrium of Gravitating System of Spherical Gas-Dust Cloud. Universal Journal of Mechanical Engineering 7(4): 192-197, 2019

Donald D. Clayton. Solar structure without computers. Am. J. Phys. 54 (4) April 1968, pp. 354-362