Vamos a describir el movimiento vertical de una esfera de masa m y de radio R, en el seno de un fluido viscoso, en régimen laminar.

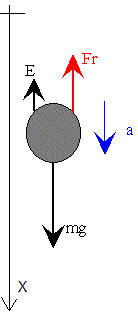
La esfera se mueve bajo la acción de las siguientes fuerzas: el peso, el empuje (se supone que el cuerpo está completamente sumergido en el seno de un fluido) y una fuerza de rozamiento que es proporcional a la velocidad de la esfera (suponemos que el flujo se mantiene en régimen laminar).

El peso es el producto de la masa por la aceleración de la gravedad g. La masa es el producto de la densidad del material ρ_e por el volumen de la esfera de radio R.

${\displaystyle mg={\rho }_e\frac{4}{3}\pi R^{3}g}$

De acuerdo con el principio de Arquímedes, el empuje es igual al producto de la densidad del fluido ρ_f, por el volumen del cuerpo sumergido y por la aceleración de la gravedad.

${\displaystyle E={\rho }_f\frac{4}{3}\pi R^{3}g}$

La fuerza de rozamiento es proporcional a la velocidad y su expresión se denomina ley de Stokes

F_r=6πRηv

donde η es la viscosidad del fluido.

La ecuación del movimiento será, por tanto,

ma=mg-E-F_r

La velocidad límite, se alcanza cuando la aceleración sea cero, es decir, cuando la resultante de las fuerzas que actúan sobre la esfera es cero.

mg-E=F_r

Despejamos la velocidad límite v_l

${\displaystyle v_l=\frac{2g({\rho }_e-{\rho }_f)R^2}{9\eta }}$

La ecuación del movimiento es

${\displaystyle \begin{array}{l}\left({\rho }_e\frac{4}{3}\pi R^3\right)\frac{dv}{dt}={\rho }_e\frac{4}{3}\pi R^{3}g-{\rho }_f\frac{4}{3}\pi R^{3}g-6\pi R\eta v\\ \frac{dv}{dt}=\mathrm{g\text{'}}-kv\mathrm{g\text{'}}=\left(1-\frac{{\rho }_f}{{\rho }_e}\right)gk=\frac{9\eta }{2{\rho }_e{R}^2}\end{array}}$

Integramos la ecuación del movimiento para obtener la velocidad de la esfera en función del tiempo, sabiendo que en el instante t=0, la velocidad v=0

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{v}{\int }}\frac{dv}{\mathrm{g\text{'}}-kv}}={\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ v=\frac{\mathrm{g\text{'}}}{k}\left(1-\exp (-kt)\right)\end{array}}$

La velocidad límite se obtiene v_l=g'/α

Esta ecuación nos dice que se alcanza la velocidad límite v_l después de un tiempo teóricamente infinito. Si representamos v en función del tiempo t la gráfica tiene una asíntota horizontal en v=v_l. Véase las dos figuras más abajo

Integramos la expresión de la velocidad en función del tiempo para obtener la posición x del móvil en función del tiempo t. Suponemos que la esfera parte del origen x=0, en el instante inicial t=0.

${\displaystyle x=\underset{0}{\overset{t}{{\displaystyle \int }}}v·dt=\frac{g\text{'}}{k}t+\frac{g\text{'}}{k^2}\left(\exp (-kt)-1\right)}$

Dado que la exponencial tiende a cero rápidamente a medida que transcurre el tiempo, vemos que al cabo de un cierto tiempo, el desplazamiento x del móvil será proporcional al tiempo t.

>> v=dsolve('Dv=G-a*v', 'v(0)=0')
v =(G - G*exp(-a*t))/a
>> x=int(v,0,t)
x =(G*(exp(-a*t) + a*t - 1))/a^2

Representamos la posición x y velocidad v en función del tiempo

rho_f=1000; %densidad agua
visco=0.00105; %viscosidad
rho_e=2700; %densidad del aluminio
R=1.9e-3; %radio de la esfera 

G=(1-rho_f/rho_e)*9.8;
k=9*visco/(2*rho_e*R^2);

tf=-log(0.0001)/k; %tiempo hasta que v es casi constante
v=@(t) G*(1-exp(-k*t))/k;
x=@(t) G*(t+exp(-k*t)/k-1/k)/k;

subplot(2,1,1)
fplot(v,[0 tf]);
grid on
xlabel('t(s)')
ylabel('v(m/s)')
title('Movimiento vertical en un fluido viscoso')

subplot(2,1,2)
fplot(x,[0 tf]);
grid on
xlabel('t(s)')
ylabel('x(m)')

• El fluido es agua de densidad ρ_f=1000 kg/m³ y viscosidad η=0.00105 kg/(m·s). La esfera de radio R=1.9·10^-3 m es de aluminio ρ_e=2700 kg/m³



La velocidad de la esfera tiende hacia un valor constante de v_l=12.73 m/s, tal como se aprecia en la figura

• El fluido es glicerina de densidad ρ_f=1260 kg/m³ y viscosidad η=1.3923 kg/(m·s). La esfera de radio R=1.9·10^-3 m es de plomo ρ_e=11350 kg/m³



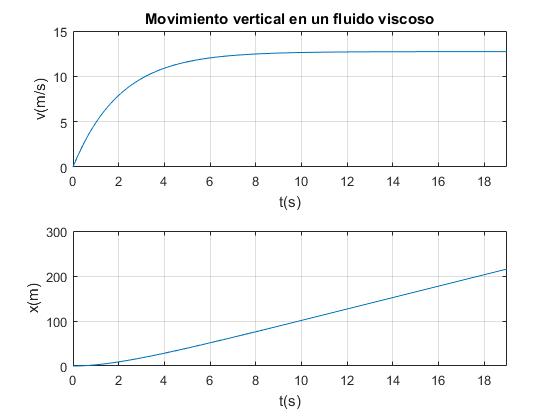
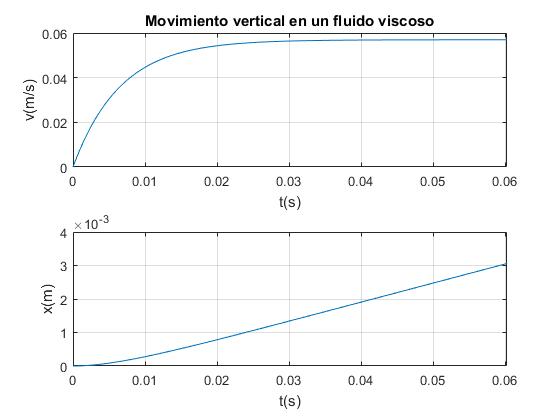
La velocidad de la esfera tiende hacia un valor constante de v_l=0.057 m/s, tal como se aprecia en la figura

Actividades

• Se elige el material de la esfera, en el control titulado Densidad esfera
• Se elige el fluido, en el control titulado Viscosidad
• El radio en mm de la esfera

Se pulsa el botón titulado Nuevo

Fuente: Koshkin N. I., Shirkévich M. G.. Manual de Física Elemental. Editorial Mir 1975.

El círculo de color rojo representa la esfera que cae en el seno de un fluido viscoso. Al lado se representa las fuerzas sobre la esfera.

• En color rojo, la fuerza F constante que es la diferencia entre el peso y el empuje del fluido.
• En color azul, la fuerza de rozamiento proporcional a la velocidad kv.

Cuando ambas flechas son aproximadamente iguales, la velocidad de la esfera es constante e igual a la velocidad límite.

Ejemplo:

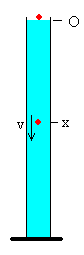
En un tubo vertical lleno de aceite de automóvil dejamos caer perdigones de plomo. El diámetro del tubo es mucho mayor que el diámetro del perdigón. Los datos son

• Densidad del plomo ρ_e=11.35 g/cm³
• Radio de la esfera R=1.96 mm
• Densidad del aceite ρ_f=0.88 g/cm³
• Viscosidad del aceite η=0.391 kg/(m·s)

Se alcanza el 99.5% de la velocidad límite constante en el instante t tal que

${\displaystyle \frac{v}{v_l}=0.995=1-\exp \left(\frac{-kt}{m}\right)}$

Donde k=6πRη=0.014 kg/s, y la masa de la esfera es m=ρ_e4/3πR³=3.58·10^-4 kg

Despejamos el tiempo t=0.13 s

La esfera se habrá desplazado en este tiempo x=0.023 m

Si dejamos caer la bolita desde la superficie del aceite, podemos comenzar a tomar medidas con seguridad 3 centímetros por debajo de dicha superficie.

En este ejemplo, se ha supuesto que el fluido se mantiene en régimen laminar cuando se mueve la esfera en su seno. Veremos más adelante, que la fórmula de Stokes tiene un rango de validez que se expresa en términos del denominado número de Reynolds.

Medida de la viscosidad, velocidad límite constante

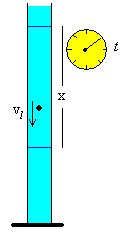
En el laboratorio se realiza una experiencia de medida de la viscosidad de un fluido, que es muy ilustrativa para los estudiantes de un curso introductorio de Física.

Se deja caer una bolita en el interior de un tubo que contiene un fluido viscoso. Se mide el tiempo que tarda la bolita en recorrer la distancia entre dos marcas hechas en el tubo. Cuando pasa por la primera marca se pone en marcha el cronómetro y cuando pasa por la segunda se para

• Se mide el diámetro de una pequeña esfera con un calibre o con un micrómetro.

• La densidad del material con el que está hecha la esfera con una balanza hidrostática.

• La densidad del fluido con un aparato denominado aerómetro o densímetro.

• Finalmente, con un cronómetro se mide el tiempo que tarda la pequeña esfera en recorrer una distancia dada en el interior del tubo vertical que contiene el fluido.

Para realizar esta experiencia se deberán cumplir dos condiciones:

• Que el número de Reynolds sea pequeño, Re<1, lo que limita el diámetro de la bolita tal como se explica en el apartado 'Fórmula de Stokes' de la página titulada 'Fuerza de rozamiento. Coeficiente de arrastre'
• Que la bolita haya alcanzado aproximadamente la velocidad límite constante cuando se empiece a medir el tiempo

Supondremos que la bolita ha alcanzado la velocidad límite constante cuando pasa por la marca superior, momento en el que se empieza a contar el tiempo. El valor de dicha velocidad se obtiene dividiendo el desplazamiento x entre el tiempo en el que tarda el móvil en desplazarse t.

${\displaystyle v_l=\frac{x}{t}}$

La velocidad límite se obtiene cuando la resultante de las fuerzas que actúan sobre la esfera es cero.

${\displaystyle v_l=\frac{2g({\rho }_e-{\rho }_f)R^2}{9\eta }}$

Ejemplo:

• Densidad del fluido 0.88 g/cm³ = 880 kg/m³
• Densidad del plomo 11.35 g/cm³ = 11350 kg/m³

Empleamos una bolita de plomo de 3.7 mm de diámetro o R=1.85 mm y la dejamos caer en una columna de aceite. El tiempo que tarda la esfera en desplazarse x=50 cm es de t=4.57 s. Calculamos la viscosidad η.

${\displaystyle \begin{array}{l}{v}_l=\frac{2g({\rho }_e-{\rho }_f)R^2}{9\eta }\\ \frac{0.5}{4.57}=\frac{2·9.8·(11350-880)·{0.00185}^2}{9\eta }\eta =0.71\text{kg/(m·s)}\end{array}}$

Medida de la viscosidad

Midiendo la velocidad límite constante, despejamos la viscosidad del fluido, tal como se hace habitualmente en el laboratorio

Sin embargo, no siempre estamos seguros que ha transcurrido suficiente tiempo, para alcanzar la velocidad límite.

Alternativamente, medimos el desplazamiento x y el tiempo t que tarda en desplazarse una esfera en el fluido viscoso, resolvemos la ecuación una ecuación trascendente para calcular k y obtener el valor de la viscosidad η

Partimos de la posición x en función del tiempo t

${\displaystyle x=\frac{g\text{'}}{k}t+\frac{g\text{'}}{k^2}\left(\exp (-kt)-1\right)}$

y de la velocidad límite constante v_l=g'/α. Definimos los parámetros adimensionales z=g't/v_l y α=2x/(g't²).

${\displaystyle \begin{array}{l}x=v_{l}t+\frac{v_l^2}{g\text{'}}\left(\exp \left(-\frac{g\text{'}}{v_l}t\right)-1\right)\\ \frac{x}{g\text{'}{t}^2}=\frac{v_l}{g\text{'}t}+{\left(\frac{v_l}{g\text{'}t}\right)}^2\left(\exp \left(-\frac{g\text{'}t}{v_l}\right)-1\right)\\ \alpha =\frac{2}{z}+\frac{2}{z^2}\left(\exp \left(-z\right)-1\right)\\ \alpha z^2-2z+2=2e^{-z}\end{array}}$

Conocido α, resolvemos la ecuación transcendente para calcular z, después la velocidad límite v_l y finalmente, la viscosidad η

Cuando el cuerpo cae en el vacío, g'=g y x=gt²/2, por lo que α=1. Para un fluido viscoso, el parámetro α deberá ser menor que 1

Ejemplo

El fluido es agua de densidad ρ_f=1000 kg/m³. La esfera de radio R=1.9·10^-3 m es de aluminio ρ_e=2700 kg/m³. La esfera se desplaza x=88.7 m en t=9 s. Calcular la viscosidad

rho_f=1000; %densidad del agua
rho_e=2700; %densidad del aluminio
R=0.0019; %radio de la bola
x=88.7; %desplazamiento
t=9; %tiempo
G=(1-rho_f/rho_e)*9.8; %gravedad g'
alfa=2*x/(G*t^2);

f=@(z) alfa*z^2-2*z+2-2*exp(-z);
raiz=fzero(f,0.5);
vl=G*t/raiz; %velocidad límite
viscosidad=2*9.8*(rho_e-rho_f)*R^2/(9*vl);
disp(viscosidad)

0.0010

Referencias

Del último apartado

Ahmed Houari. Determining the viscosity of liquids using an extended falling ball method. Physcis Education 46 (6) 2011, pp. 688-691