Oscilaciones transversales de un imán
El dispositivo experimental consta de un par de bobinas de Helmholtz de radio R y que constan de N espiras cada una, conectadas a una batería de modo que la corriente recorre las espiras en el mismo sentido. Las bobinas se disponen paralelamente a una distancia R una de la otra. Un pequeño imán de momento dipolar se cuelga de un hilo de modo que esté situado en el punto medio del eje de las bobinas.
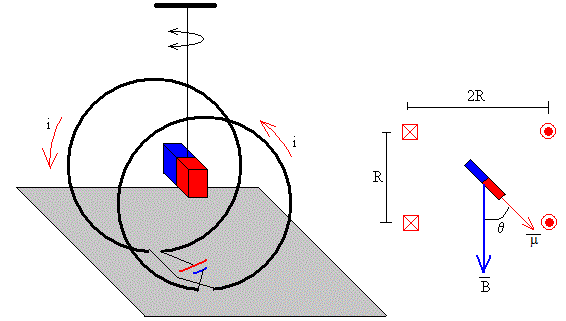
Cuando el eje del imán no coincide con el eje de las bobinas el campo magnético ejerce un momento que tiende a orientar su momento dipolar en la dirección del campo. Como veremos el imán describe aproximadamente un Movimiento Armónico Simple (M.A.S.), cuyo periodo medimos con un cronómetro.
El campo magnético producido por una bobina de radio R, de N espiras, recorrida por una corriente de intensidad i, en un punto de su eje que dista x de su centro es
Su dirección es la del eje de la bobina y su sentido está dado por la regla de la mano derecha, el señalado en la figura.
El campo producido por dos bobinas iguales, recorridas por la misma corriente i, en el punto medio del eje común de las bobinas x=R/2 es
Los campos producidos por las dos bobinas tienen el mismo módulo, la misma dirección y el mismo sentido.
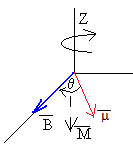
Si el imán se separa un ángulo pequeño θ del eje de las bobinas, se ejerce sobre él un momento
-
El módulo del momento es M=μB·sinθ
-
La dirección, el eje de rotación Z
-
Sentido el indicado en la figura.
La ecuación de la dinámica de rotación alrededor de un eje fijo Z se escribe
I·α=-Kθ-μB·sinθ
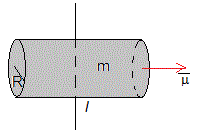
K es la constante de torsión del hilo, α la aceleración angular, I es el momento de inercia del imán, que depende de la forma y dimensiones del imán, por ejemplo, para un imán cilindrico de masa m, longitud l y radio R
Expresando la ecuación del movimiento en forma de ecuación diferencial
No es la ecuación diferencial de un MAS. Ahora bien, si la amplitud de la oscilación es pequeña, hacemos la aproximación sinθ≈θ.
Tenemos entonces, la ecuación diferencial de un MAS de frecuencia angular
La representación gráfica de ω2=4π2/P2 en función del campo magnético B será una línea recta. Midiendo la pendiente de la recta calculamos el momento dipolar magnético μ del imán
Si el imán parte de la posición θ0 en el instante t=0, con velocidad angular inicial dθ/dt=0, la ecuación del MAS, es
θ=θ0·cos(ωt)
Energía potencial de un dipolo magnético en un campo magnético
Cuando un momento actúa sobre un cuerpo y éste gira un determinado ángulo, se realiza un trabajo. Cuando el dipolo gira un ángulo dθ, el trabajo realizado es
dW=-M·dθ=-μBsinθ·dθ
El signo menos aparece por que el momento tiende a disminuir el ángulo θ,
Como el trabajo de una fuerza conservativa es igual a la variación de energía potencial cambiada de signo (definición de energía potencial)
dEp=-dW=μBsinθ·dθ
Integrando
Ep=-μBcosθ+C
Donde C es una constante aditiva que nos permite establecer el nivel cero de energía potencial. La energía potencial es nula cuando θ=90º, luego, C=0.
La energía potencial es el producto escalar de dos vectores, el momento magnético y el campo magnético .
Actividades
Disponemos de un imán cilíndrico de masa m=0.0511 kg, longitud l=0.125 m, radio R=0.0046 m. El momento de inercia repecto de un eje perpendicular al cilindro que pasa por el centro de masa es
I= 6.6807·10-5 kg·m2
El programa interactivo genera aleatoriamente un valor del momento magnético μ comprendido entre 2.0 y 5.0 A·m2
-
Se introduce el campo magnético B producido por las bobinas, en el control titulado Campo magnético en gauss (10-4 T).
Se pulsa el botón titulado Nuevo
Las bobinas de Helmholtz tiene las siguientes características:
- El dámetro 2R de las bobinas, es 0.21 m
- El número de espiras de cada bobina N=119
B=0.001·i T. Donde i es la intensidad en A
Medimos el periodo P=2π/ω de las oscilaciones para un campo magnético B dado , para ello, utilizamos los botones pausa || y paso a paso >|
| Campo magnético, B·10-4 T | Periodo (s) |
|---|---|
| 2 | 1.88 |
| 4 | 1.40 |
| 6 | 1.16 |
| 8 | 1.01 |
| 10 | 0.91 |
| 12 | 0.83 |
| 14 | 0.77 |
Representamos en el eje X, el campo magnético B, en el eje Y, (2π/P)2
La pendiente de la recta que mejor ajusta a los datos 'experimentales' es el cociente μ/I. Sabiendo el momento de inercia I calculamos el momento dipolar μ en A·m2
>> >> x=(2:2:14)/10000; >> P=[1.88,1.40,1.16,1.01,0.91,0.83,0.77]; >> y=4*pi^2./P.^2; >> plot(x,y,'ro','markersize',4,'markerfacecolor','r')
En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p1=46234 y p2=1.7152 del polinomio (recta) y=p1*x+p2 de ajuste.
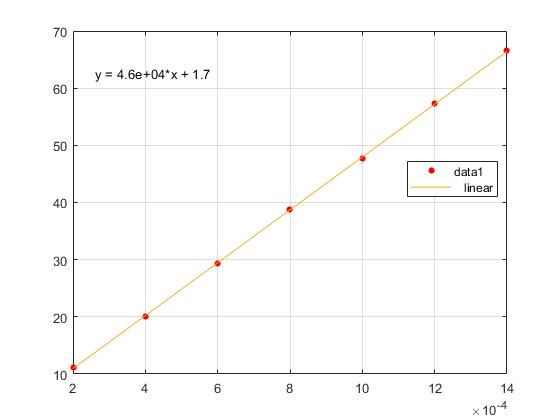
El momento dipolar del imán es
6.6807e-5*46234 ans = 3.0888
Oscilaciones forzadas
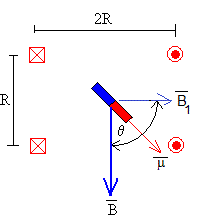
Supongamos que creamos un campo perpendicular al campo producido por las dos bobinas de Helmholtz, cuyo módulo varía con el tiempo de la forma B1sin(ωft).
El momento sobre el imán es μ·B1sin(ωft)sin(90-θ)=μ·B1sin(ωft)cos(θ), la dirección es el eje de rotación Z y sentido el contrario al del momento producido por el campo de las bobinas B.
Consideraremos además, que existe un rozamiento que produce un momento proporcional a la velocidad angular de rotación y de sentido contrario a ésta, Mr=-λdθ/dt. La ecuación diferencial del movimiento se escribe
Con 2γ=λ/I, F0=μB1/I. Si la amplitud de la oscilación es pequeña, hacemos la aproximación sinθ≈θ, cosθ≈1.
Hemos llegado a la ecuación diferencial de las oscilaciones forzadas. En el estado estacionario la solución es
La amplitud A0 es máxima para la frecuencia angular ωm
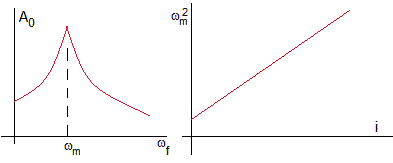
El cuadrado de la frecuencia ωm (correspondiente al máximo de la amplitud) es proporcional a la intensidad i de la corriente que pasa por las bobinas de Helmholtz. La pendiente de la recta, es proporcional al momento magnético del imán μ y la intersección con el eje Y nos proporciona una medida de la constante de amortiguamiento λ si conocemos los valores de la constante de torsión K del hilo y del momento de inercia del imán I respecto del eje de giro.
Referencias
B. Barman, A. Petrou Measuring the magnetization of a permanent magnet. Am. J. Phys. 87 (4) April 2019, pp. 275-278.
Gaylord T. Hageseth. Forced Oscillations and Magnetic Resonance in the Introductory Laboratory. Am. J. Phys. 37 (5) May 1969, pp. 529-531

