Aplicaciones de la fuerza magnética
Cañón electromagnético
Para demostrar la fuerza que ejerce un campo magnético sobre una corriente eléctrica se construye un dispositivo consistente en un potente imán que produce un campo de 500 gauss o B=0.05 T, sobre cuyo polo norte se pegan dos raíles hechos con láminas de cobre. La porción de conductor es una varilla de cobre de L=15 cm de longitud.
La corriente se suministra mediante una descarga en arco de i=60 A. La corriente y el campo son perpendiculares, por lo que la fuerza sobre la varilla es
Fm=iBL=0.05·60·0.15=0.45 N
Si la masa de la varilla es de 1.35 g, su aceleración es de 333.3 m/s2. Las elevadas aceleraciones conseguidas podrían sugerir que se podría emplear la varilla como proyectil de un cañón electromagnético.
La velocidad de la varilla al final de los raíles de 50 cm es
Una varilla, que se mueve en un campo magnético uniforme produce una corriente inducida, que no hemos tenido en cuenta en este modelo simplificado, un estudio más detallado se encuentra en la página titulada Varilla que se mueve en un campo magnético uniforme. Efecto de la batería
Actividades
Se introduce
- La intensidad del campo magnético (gauss), en el control titulado Campo magnético
- Intensidad de la corriente (A), en el control titulado Intensidad
- Longitud de la varilla, entre 5 y 20 cm, en el control titulado Longitud
- Masa de la varilla (g), en el control titulado Masa
Se pulsa el botón titulado Nuevo,
Se observa el movimiento de la varilla. En la parte superior, se proporciona la posición y velocidad de la varilla en función del tiempo.
La rueda de Barlow
Hemos estudiado la fuerza que ejerce una campo magnético sobre una porción de corriente rectilínea que circula por un conductor que puede deslizar sin rozamiento en contacto con dos rieles paralelos.
Ahora, vamos a estudiar el momento de la fuerza que ejerce el campo magnético sobre la corriente que circula entre el centro y el borde de un disco.
La rueda de Barlow es un disco de cobre que está situada entre los polos de un imán y cuyo borde está en contacto con un pequeño depósito de mercurio. Se conecta una batería entre el eje de la rueda y el depósito de mercurio y se observa que la rueda empieza a girar alcanzando una velocidad angular límite constante.
Comprobaremos que dicha velocidad angular es proporcional a la intensidad de la corriente.
La rueda de Barlow es reversible en el sentido de que si se quita la batería y se la hace girar aplicando una fuerza externa, se puede medir la corriente inducida generada. En la página titulada un disco, motor y generador eléctrico, estudiaremos con detalle el papel jugado por la corriente inducida en el movimiento de la rueda de Barlow.
Fuerza que ejerce el campo magnético
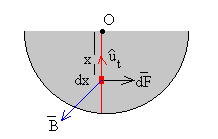
La fuerza sobre un elemento de corriente dx situado a una distancia x del eje del disco es
Su módulo es dF=iB·dx y está dirigido como vemos en la figura, hacia la derecha.
El momento de esta fuerza respecto del eje del disco es dM=x·dF, y el momento total
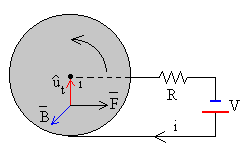
La fuerza resultante F=iBa que produce un momento total M estará aplicada en el punto medio del radio a/2 tal como se muestra en la figura.
Se puede demostrar (véase el artículo citado en las referencias) que el momento M no cambia si la rueda en vez de ser maciza consta de cuatro brazos que sostienen un anillo de cobre tal como se muestra en el programa interactivo al final de esta página.
Fuerza de rozamiento
En el eje del disco se produce un momento debido al rozamiento entre el eje y los rodamientos que se puede suponer que es proporcional a la velocidad angular de la rueda.
Mr=-kω
La constante de proporcionalidad depende del radio del eje, viscosidad del aceite lubrificante, etc.
Ecuación del movimiento
La ecuación del movimiento de un sólido rígido en rotación alrededor de un eje fijo es
Donde I0 es el momento de inercia de la rueda.
Integramos esta ecuación con las condiciones iniciales t=0, ω =0, obteniendo la velocidad angular ω de la rueda en cualquier instante t.
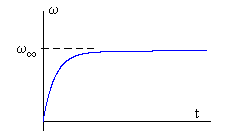
La velocidad angular crece desde cero hasta un valor límite constante
Integrando de nuevo obtenemos el ángulo girado θ por la rueda en función del tiempo t.
Cuando se alcanza el estado estacionario (el valor de la exponencial tiende a cero), la velocidad angular de rotación tiende hacia un valor constante y el ángulo girado por la rueda es proporcional al tiempo. Una situación análoga a la de una esfera que cae en el seno de un fluido viscoso.
Las medidas experimentales reales indican que el estado estacionario se alcanza inmediatamente, de modo que se observa una relación lineal entre el ángulo girado en función del tiempo. En la simulación, tomaremos un valor pequeño de k de modo que se pueda observar la evolución desde el estado inicial en reposo hasta el estado estacionario.
Actividades
Se ha simulado el comportamiento de un disco de cobre (de densidad 8.93 g/cm3) de radio 10 cm y de 1 mm de espesor, cuya masa es m=8.93·103·π ·(0.1)2·0.001=0.280 kg, y cuyo momento de inercia es I0=ma2/2=0.280·(0.1)2/2=0.001403 kgm2.
El programa fija la constante k de proporcionalidad del momento de la fuerza de rozamiento, en un valor aleatorio comprendido entre ciertos límites. También, fija el radio del disco en a=10 cm
- Se introduce el valor (positivo o negativo) de la intensidad del campo magnético B, en el control titulado C. magnético.
- Se introduce el valor (positivo o negativo) de la intensidad de la corriente i, en el control titulado Intensidad
Se pulsa el botón titulado Nuevo.
Ejemplo:
- La intensidad del campo magnético B=0.1 T
- El radio del disco a=10 cm=0.1 m
Para los siguientes valores de la intensidad i, se obtienen los siguientes de la velocidad angular límite ω∞
| i | 2 | 5.5 | 10 | 15 |
|---|---|---|---|---|
| ω∞ | 0.32 | 0.91 | 1.66 | 2.49 |
La relación lineal entre ω∞ y la intensidad i es
intensidad=[2, 5.5, 10, 15];
w=[0.32,0.91,1.6,2.49];
plot(intensidad, w,'ro','linewidth',1,'markersize',4,'markeredgecolor',
'b','markerfacecolor','b')
title('Rueda de Barlow')
xlabel('i(A)')
ylabel('\omega')
grid on
En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p1 y p2 del polinomio (recta) y=p1*x+p2 de ajuste.
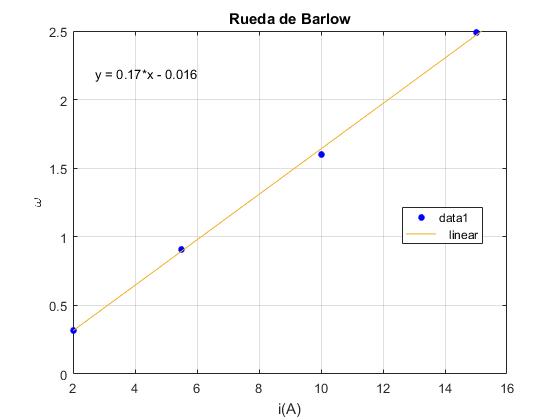
Conocido el valor de la pendiente de la recta Ba2/(2k), 0.16567. El valor de la constante k de proporcionalidad del momento de la fuerza de rozamiento es
Referencias
R. Jones. The rail gun: A popular demonstration of the Lorentz force. Am. J. Phys. 68 (8) August 2000, pp. 773-774
Maroto J. A, de Dios J., de las Nieves J. Evaluation of the Lorentz Law by Using a
Barlow Wheel. IEEE Transactions on Education Vol. 41, nº 3, August 2000.
Los autores han catalogado un
conjunto de instrumentos antiguos clasificados por áreas: Mecánica, Fluidos...

