Amperímetro. Edimburgo, 7 de enero de 2017

Fuerza sobre cada lado de la espira

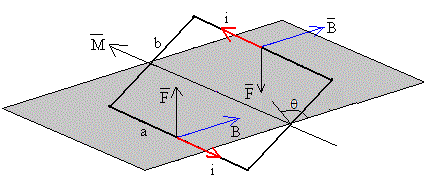
La figura representa una espira rectangular cuyos lados miden a y b. La perpendicular al plano de la espira forma un ángulo θ o la espira forma un θ-π/2 con el plano horizontal. La espra es recorrida por una corriente de intensidad i, tal como indica el sentido de la flecha roja en la figura.

La espira está situada en una región en la que hay un campo magnético uniforme B paralelo al plano horizontal (en color gris), tal como indica la flecha de color azul en la figura.

Calcularemos la fuerza que ejerce dicho campo magnético sobre cada uno de los lados de la espira rectangular.

Ya hemos deducido la expresión de la fuerza que ejerce un campo magnético sobre una porción L de corriente rectilínea.

${\displaystyle \overrightarrow{F_m}=i{\widehat{u}}_t\times \overrightarrow{B}·L}$

donde, ${\widehat{u}}_t$ es un vector unitario que nos señala la dirección y el sentido en el que se mueven los portadores de carga positivos.

• La fuerza F₁ sobre cada uno de los lados de longitud a, está señalada en la figura y su módulo vale

F₁=i·1·B·a·sin90º=iBa.

• La fuerza F₂ sobre cada uno de los lados de longitud b, es



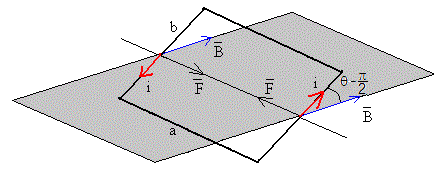
F₂=i·1·B·b·sinθ =iBb·sin(θ-π/2)=iBbcosθ

Esta fuerza tiene la dirección del eje de rotación de la espira y sentidos opuestos.

La fuerza F₂ es nula cuando la espira está contenida en el plano horizontal θ=0º y es máxima, cuando el plano de la espira es perpendicular al plano horizontal θ=90º.

Momento de las fuerzas sobre la espira

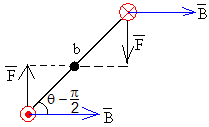
La fuerza resultante sobre la espira es nula, sin embargo, las fuerzas sobre los lados de longitud a no tienen la misma línea de acción y forman un par de momento.

M=2F₁·(b/2)·cos(θ-π/2) =i·ab·B·sinθ =i·S·B·sinθ

La dirección momento $\overrightarrow{M}$ es la del eje de rotación de la espira y el sentido viene dado por la regla del sacacorchos, tal como se señala en la primera figura.

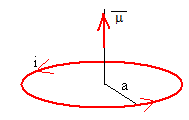
Definimos una nueva magnitud denominada momento magnético $\overrightarrow{\mu }$ de la espira.

• Cuyo módulo es el producto de la intensidad de la corriente i por el área S de la espira.
• Su dirección es perpendicular al plano de la espira.
• Su sentido viene determinado por el avance de un sacacorchos que gire como lo hace la corriente en la espira.

El momento se puede expresar en forma de producto vectorial de dos vectores, el vector momento magnético $\overrightarrow{\mu }$ y el vector campo magnético $\overrightarrow{B}$.

${\displaystyle \overrightarrow{M}=\overrightarrow{\mu }\times \overrightarrow{B}}$

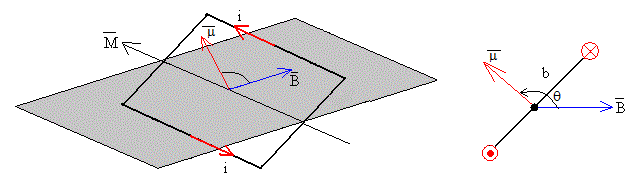
Como vemos en la figura

• Su módulo es M=μ·B·sinθ=iS·B·sinθ
• Su dirección es perpendicular al plano determinado por los dos vectores, es decir, el eje de rotación de la espira.
• Su sentido es el del avance de un sacacorchos que gire desde el vector $\overrightarrow{\mu }$ hacia el vector $\overrightarrow{B}$ por el camino más corto.

Cuando el vector campo $\overrightarrow{B}$ y el vector momento magnético $\overrightarrow{\mu }$ son paralelos, el momento $\overrightarrow{M}$ es nulo.

Motor de corriente continua

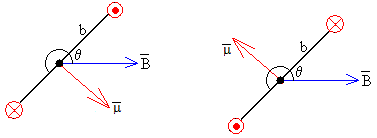
Cuando la espira incrementa en π (180°) el ángulo girado, el momento $\overrightarrow{M}$ cambia de sentido (a la izquierda en la figura). Si queremos que el momento no cambie, la corriente tiene que cambiar de sentido (a la derecha en la figura)

En un motor de corriente continua, las espiras tienen un conmutador que invierte el sentido de la corriente después de media vuelta, de modo que el momento magnético de las espiras es

${\displaystyle \begin{array}{l}\{\begin{array}{l}\overrightarrow{\mu }=+{\mu }_0\widehat{n},0\le \theta <\pi \\ \overrightarrow{\mu }=-{\mu }_0\widehat{n},\pi \le \theta <2\pi \end{array}\\ {\mu }_0=NiS\\ M={\mu }_{0}B\left|\sin \theta \right|\end{array}}$

N es el número de espiras y el ángulo θ se refiere al resto de la división entre el ángulo girado y 2π. Si las espiras tienen una resistencia R

${\displaystyle M=N\frac{V_0}{R}SB\left|\sin \theta \right|=N\frac{V_0\mathrm{sgn}\left(\sin \theta \right)}{R}SB\sin \theta }$

El símbolo sgn se refiere al signo de sinθ

Aunque la fórmula del momento $\overrightarrow{M}$ se ha obtenido para espiras rectangulares, es válida para espiras circulares o de cualquier otra forma.

El momento de inercia de N espiras de masa m respecto del eje de rotación

${\displaystyle \begin{array}{l}I=N\left\{2\left(\lambda a\right){\left(\frac{b}{2}\right)}^2+2\frac{1}{12}\left(\lambda b\right)b^2\right\}=N\lambda b^2\frac{1}{2}\left(a+\frac{b}{3}\right)=\\ N\frac{m}{N4\left(a+b\right)}{b}^2\left(a+\frac{b}{3}\right)=\frac{m}{4\left(a+b\right)}{b}^2\left(a+\frac{b}{3}\right)\end{array}}$

λ es la masa por unidad de longitud

La ecuación de la dinámica de rotación es

${\displaystyle I\frac{d^2\theta }{d{t}^2}=N\frac{V_0}{R}SB\left|\sin \theta \right|-M_{ext}}$

donde M_ext se refiere al momento externo (de la carga debida a los dispositivos mecánicos conectados al eje del motor y al rozamiento)

Estableciendo una escala de tiempos, la ecuación diferencial se hace más simple

${\displaystyle \begin{array}{l}\tau =t\sqrt{N\frac{V_0}{I·R}SB}\\ \frac{d^2\theta }{d{\tau }^2}=\left|\sin \theta \right|-\beta ,\beta =M_{ext}\frac{R}{N{V}_{0}SB}\end{array}}$

Resolvemos la ecuación diferencial con β=0, por el procedimiento ode45 de MATLAB con las siguientes condiciones iniciales: en el instante τ=0, θ=π/2, dθ/dτ=0. Representamos la velocidad angular dθ/dτ en función del tiempo τ

f=@(t,x) [x(2);abs(sin(x(1)))]; 
[t,x]=ode45(f,[0,12],[pi/2,0]);
plot(t,x(:,2))
grid on
xlabel('\tau')
ylabel('d\theta/d\tau');
title('Motor de corriente continua')

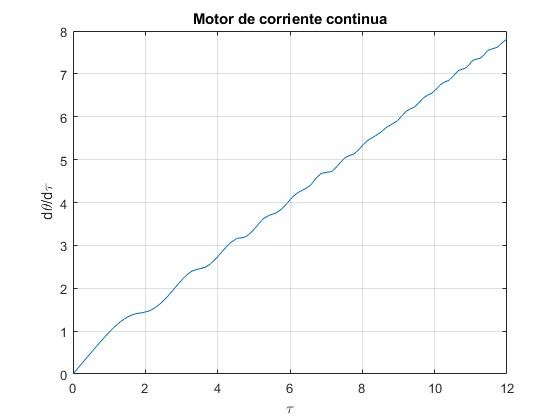
La velocidad angular crece sin límite

No se ha tenido en cuenta, que una espira que gira en un campo magnético uniforme produce una fem inducida, debido a que el flujo del campo magnético que la atraviesa cambia con el tiempo. Esta situación se describe en la página titulada Motor de corriente continua