Campo magnético producido por una corriente rectilínea indefinida (I)
El físico Jean Biot dedujo en 1820 una ecuación que permite calcular el campo magnético creado por un circuito de forma cualesquiera recorrido por una corriente de intensidad i.
es el vector campo magnético existente en un punto P del espacio, es un vector unitario cuya dirección es tangente al circuito y que nos indica el sentido de la corriente en la posición donde se encuentra el elemento dl. es un vector unitario que señala la posición del punto P respecto del elemento de corriente, la distancia entre ambos es r. La constante μ0/(4π)=10-7 en el Sistema Internacional de Unidades.

Corriente rectilínea perpendicular al plano de la fotografía
Campo magnético producido por una corriente rectilínea
Utilizamos la ley de Biot para calcular el campo magnético producido por un conductor rectilíneo indefinido por el que circula una corriente de intensidad i.
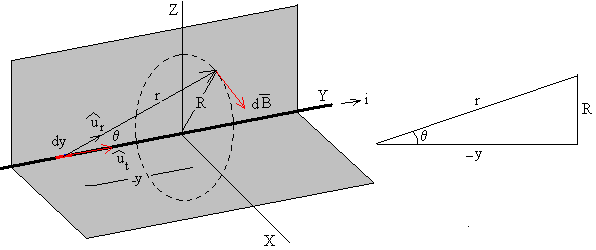
El campo magnético producido por el hilo rectilíneo en el punto P tiene por dirección la perpendicular al plano formado por la corriente rectilínea y el punto P, y sentido el que resulta de la aplicación de la regla del sacacorchos al producto vectorial . Para calcular el módulo de dicho campo es necesario realizar una integración.
Se integra sobre la variable θ, expresando las variables x y r en función del ángulo θ .
R=r·sinθ , R=-y·tanθ .
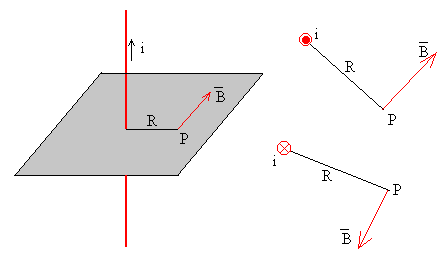
En la figura, se muestra la dirección y sentido del campo magnético producido por una corriente rectilínea indefinida en el punto P. Cuando se dibuja en un papel, las corrientes perpendiculares al plano del papel y hacia el lector se simbolizan con un punto • en el interior de una pequeña circunferencia, y las corrientes en sentido contrario con una cruz × en el interior de una circunferencia tal como se muestra en la parte derecha de la figura.
La dirección del campo magnético se dibuja perpendicular al plano determinado por la corriente rectilínea y el punto y el sentido se determina por la regla del sacacorchos o la denominada de la mano derecha.
Campo magnético producido por un segmento de corriente

Calculamos el campo magnético producido por un segmento de corriente AB en el punto P distante R. Los límites de la integral son ahora, θ1 y π-θ2
Para una corriente indefinida θ1→0 y θ2→0
Supongamos que el punto P es el centro de una espira cuadrada de lado l, por la que circula una corriente de intensidad i en el sentido indicado en la figura
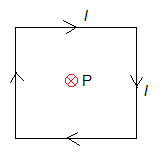
Poniendo θ1=θ2=45° y R=l/2. El campo magnético producido por un lado de la espira es
Los campos magnéticos producidos por cada uno de los lados en el centro P de la espira tienen la misma dirección (perpendicular al plano de la espira) y sentido
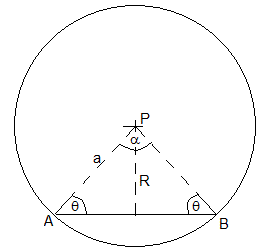
En general, para una espira en forma de polígono regular de radio a y n lados, el campo magnético producido en su centro P por el segmento de corriente AB, se obtiene poniendo α=2π/n, θ1=θ2=π/2-π/n, R=acos(π/n)
Los campos magnéticos producidos por cada uno de los lados en el centro P del polígono regular tienen la misma dirección (perpendicular al plano del polígono) y sentido
Cuando n→∞, tan(π/n)→π/n, y el campo producido por la espira circular de radio a en su centro vale
La ley de Ampère
La ley de Gauss nos permitía calcular el campo eléctrico producido por una distribución de cargas cuando estas tienen simetría (esférica, cilíndrica o un plano cargado).
Del mismo modo, la ley de Ampère nos permitirá calcular el campo magnético producido por una distribución de corrientes cuando tienen cierta simetría.
Los pasos que hay que seguir para aplicar la ley de Ampère son similares a los de la ley de Gauss.
- Dada la distribución de corrientes, deducir la dirección y sentido del campo magnético
- Elegir un camino cerrado apropiado, atravesado por corrientes y calcular la circulación del campo magnético.
- Determinar la intensidad de la corriente que atraviesa el camino cerrado
- Aplicar la ley de Ampère y despejar el módulo del campo magnético.
Campo magnético producido por una corriente rectilínea
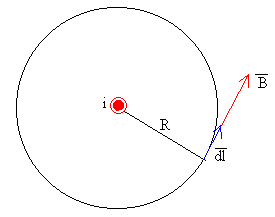
- La dirección del campo en un punto P, es perpendicular al plano determinado por la corriente y el punto.
- Elegimos como camino cerrado una circunferencia de radio r, centrada en la corriente rectilínea y situada en una plano perpendicular a la misma.
- El campo magnético es tangente a la circunferencia de radio r, paralelo al vector .
- El módulo del campo magnético tiene tiene el mismo valor en todos los puntos de dicha circunferencia.
- La corriente rectilínea i atraviesa la circunferencia de radio r
- Despejamos el módulo del campo magnético B.
La circulación (el primer miembro de la ley de Ampère) vale
Llegamos a la expresión obtenida aplicando la ley de Biot.
Fuerza entre dos corrientes rectilíneas
Sean dos corrientes rectilíneas indefinidas de intensidades Ia e Ib paralelas y distantes d.
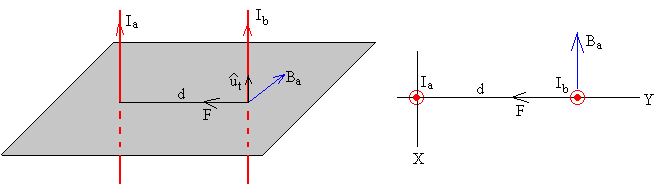
El campo magnético producido por la primera corriente rectilínea en la posición de la otra corriente es
De acuerdo con la regla de la mano derecha tiene el sentido indicado en la figura, en forma vectorial
La fuerza sobre una porción L, de la segunda corriente rectilínea por la que circula una corriente Ib en el mismo sentido es
La fuerza que ejerce el campo magnético producido por la corriente de intensidad Ib sobre la una porción de longitud L de corriente rectilínea de intensidad Ia, es igual pero de sentido contrario.
La fuerza por unidad de longitud ente dos corrientes rectilíneas indefinidas y paralelas, distantes d es
La unidad de medida de la intensidad de la corriente eléctrica, el ampere, se fundamenta en esta expresión:
El ampere (A) es la intensidad de una corriente constante que manteniéndose en dos conductores paralelos, rectilíneos, de longitud infinita, de sección circular despreciable y situados a una distancia de un metro uno de otro en el vacío, produciría una fuerza igual a 2·10-7 newton por metro de longitud.
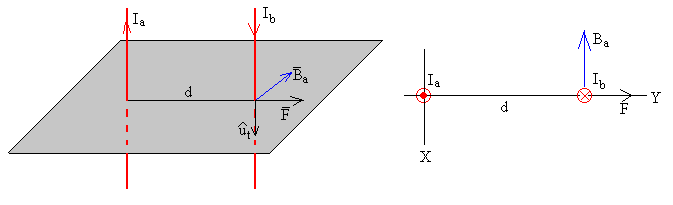
Si las corrientes tienen sentido opuesto, la fuerza tiene el mismo módulo pero de sentido contrario, las corrientes se repelen, tal como se aprecia en la figura
Dos corrientes rectilíneas indefinidas, paralelas, separadas una distancia d
- las corrientes eléctricas que circulan en el mismo sentido, se atraen
- las corrientes eléctricas que circulan en sentido contrario, se repelen
Medida del campo magnético terrestre

Colocamos un hilo rectilíneo en la dirección del campo magnético terrestre. Cuando hacemos pasar una corriente por el hilo, la aguja se desvía

La corriente rectilínea crea en la posición de la aguja de la brújula un campo magnético, cuyo módulo es
cuya dirección y sentido se indican en la figura. La aguja se desvía una ángulo θ. Midiendo este ángulo obtenemos el valor de la componente horizontal del campo magnético terrestre BT
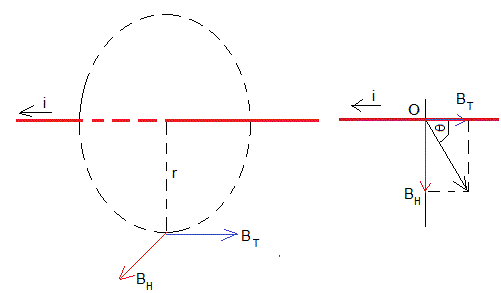
Sabiendo que la intensidad i=2.13 A, la distancia r=3 mm y el ángulo girado por la brújula, θ=45°, obtenemos BT=1.42·10-4 T
El mayor dificultad de esta experiencia reside en medir la distancia de la corriente a la aguja de la brújula. Aunque los resultados del experimento no sean buenos, sin embargo, es un ejemplo ilustrativo de la interacción entre corrientes e imanes
Referencias
Fotografía tomada en VIII Edición del Concurso Ciencia en Acción Zaragoza (2007): Albert Agraz Sánchez, Santiago Clúa. Detector de movimiento por inducción magnética. Universidad de Lérida.
Para el apartado, medida del campo magnético terrestre
Brandon Lunk, Robert Beichner. Exploring Magnetic Fields with a Compass. The Physics Teacher, Vol. 49, January 2011, pp. 45-48

