Cañón magnético

Campo magnético de un solenoide

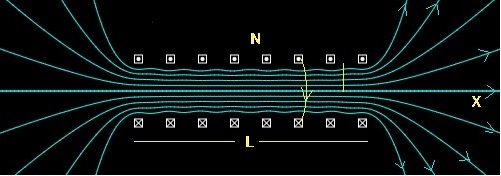
El campo magnético producido en un punto x del eje de un solenoide de N espiras, longitud L y radio a, por el que circula una corriente de intensidad I es

$B = \frac{μ_{0} I N}{2 L} (\frac{L / 2 - x}{\sqrt{{(L / 2 - x)}^{2} + a^{2}}} + \frac{L / 2 + x}{\sqrt{{(L / 2 + x)}^{2} + a^{2}}})$

Ejemplo:

El radio del solenoide, a=3.9 mm
El número de espiras, N=184.
La longitud del solenoide, L=50.8 mm
La intensidad de la corriente, I=200 A

Representamos el campo magnético B en cada punto x del eje del solenoide

L=50.8/1000; %longitud del solenoide
a=3.9/1000; %radio solenoide, 
N=184;  %número de espiras
I=200; %corriente, amperios

B0=4*pi*1e-7*N*I/L; %campo magnético uniforme
B=@(x) ((L/2-x)./sqrt((L/2-x).^2+a^2)+(L/2+x)./sqrt((L/2+x).^2+a^2))/2;
fplot(B,[-L,L]);

line([L/2,L/2],[0,B(L/2)],'lineStyle','--', 'color','k')
line([-L/2,-L/2],[0,B(-L/2)],'lineStyle','--', 'color','k')
grid on
xlabel('x (m)')
ylabel('B (T)')
title('Campo magnético en el eje de un solenoide')

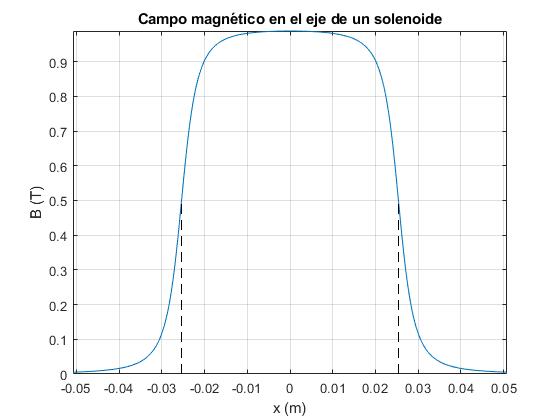
Las líneas verticales, señalan los extremos del solenoide, cuyo centro está en el origen

Cuando el radio a del solenoide es mucho más pequeño que su longitud L, el campo magnético es prácticamente uniforme en el interior del solenoide. Un poco más allá de los extremos del solenoide, el campo magnético se reduce a cero

Oscilaciones del imán

Supongamos que un imán de masa m, longitud d y momento magnético μ, se sitúa en el eje del solenoide. La fuerza que ejerce el campo magnético producido por el solenoide sobre el imán es

$F (x) = \frac{μ}{d} (B (x + \frac{d}{2}) - B (x - \frac{d}{2}))$

Ejemplo:

El radio del solenoide, a=3.9 mm
El número de espiras, N=184.
La longitud del solenoide, L=50.8 mm
La intensidad de la corriente, I=200 A
La longitud del imán, d=12.7 mm
El momento magnético del imán, μ=0.455 A·m²
La masa del imán, m=0.003 kg

Representamos la fuerza F que ejerce el campo magnético producido por el solenoide sobre el imán, en función de su posición x a lo largo del eje del solenoide

L=50.8/1000; %longitud del solenoide
a=3.9/1000; %radio solenoide, 
N=184;  %número de espiras
mu=0.455; %Am^2, momento magnético del imán
d=12.7/1000; %longitud del imán
I=200; %corriente, amperios

B0=4*pi*1e-7*N*I/L; %campo magnético constante
B=@(x) B0*((L/2-x)./sqrt((L/2-x).^2+a^2)+(L/2+x)./sqrt((L/2+x).^2+a^2))/2;
F=@(x) mu*(B(x+d/2)-B(x-d/2))/d; %fuerza
fplot(F,[-1*L,1*L]);

line([L/2,L/2],[0,F(L/2)],'lineStyle','--', 'color','k')
line([-L/2,-L/2],[0,F(-L/2)],'lineStyle','--', 'color','k')
grid on
xlabel('x (m)')
ylabel('F (N)')
title('Fuerza')

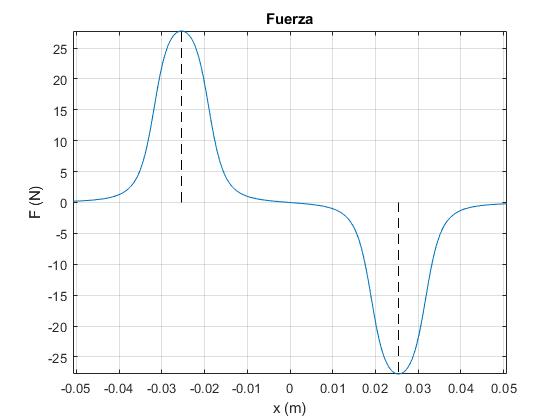
Las líneas verticales, señalan los extremos del solenoide, cuyo centro está en el origen

La fuerza sobre el imán es máxima en los extremos del solenoide, es nula en el centro, y tiende a cero cuando nos alejamos de los extremos del solenoide

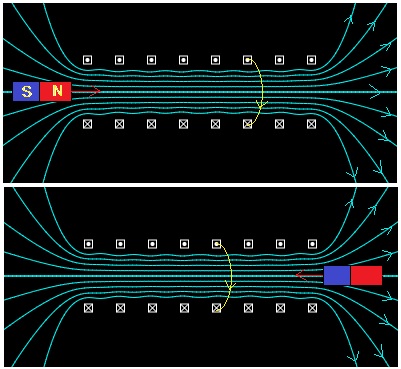
Cuando se sitúa un imán de masa m en las proximidades del solenoide tal como se muestra en la figura, es atraído hacia el interior del solenoide, adquiere la máxima velocidad cuando pasa por el centro, hasta que llega al otro extremo. El imán se frena (la fuerza que experimenta es de sentido contrario a su velocidad) y vuelve hacia el interior del solenoide.

El imán oscila con un periodo que podemos determinar resolviendo la ecuación diferencial del movimiento a lo largo del eje del solenoide,

$\frac{d^{2} x}{d t^{2}} = \frac{F (x)}{m}$

por procedimientos numéricos, con las siguientes condiciones iniciales: en el instante t=0, x=x₀, dx/dt=0. Parte del reposo en las proximidades del extremo izquierdo del solenoide.

El procedimiento ode45 de MATLAB no da buenos resultados, para fuerzas que cambian rápidamente, por lo que probamos el procedimiento ode23, que se comporta correctamente durante varias oscilaciones, siempre que la posición inicial x₀ no esté demasiado alejada del extremo del solenoide.

Calculamos, medio periodo de oscilación, definiendo una función que nos proporcione el tiempo que tarda el imán en volver a estar momentáneamente en reposo, dx/dt=0

function [value,isterminal,direction]=coilgun_periodo(t,x)
    value=x(2); %detecta velocidad nula
    isterminal=0;
    direction=-1; 
end

Resolvemos la ecuación diferencial por el procedimiento ode23 y representamos el movimiento del imán en el espacio de las fases, en el eje horizontal, la posición x, y en el eje vertical, la velocidad dx/dt. Las líneas verticales señalan el movimiento del imán en el interior del solenoide, que en su mayor parte es rectilíneo y uniforme.

a=3.9/1000; %radio solenoide
L=50.8/1000; %longitud del solenoide
N=184;  %número de espiras
I=200; %corriente, amperios
mu=0.455; %Am^2, momento magnético del imán
m=0.003; %kg, masa del imán 
d=12.7/1000; %longitud del imán

tf=0.015; %tiempo final
x0=-0.7*L; %posición de partida en reposo
B0=4*pi*1e-7*N*I/L; %campo magnético uniforme
B=@(x) B0*((L/2-x)./sqrt((L/2-x).^2+a^2)+(L/2+x)./sqrt((L/2+x).^2+a^2))/2; 
F=@(x) mu*(B(x+d/2)-B(x-d/2))/d; %fuerza
fg=@(t,x)[x(2);F(x(1))/m];
opts=odeset('events',@coilgun_periodo);
[t,x,te]=ode23(fg,[0,tf],[x0,0],opts);
plot(x(:,1),x(:,2))

line([L/2,L/2],[-20,20],'lineStyle','--', 'color','k')
line([-L/2,-L/2],[-20,20],'lineStyle','--', 'color','k')
grid on
xlabel('x')
ylabel('v')
title('Oscilaciones')

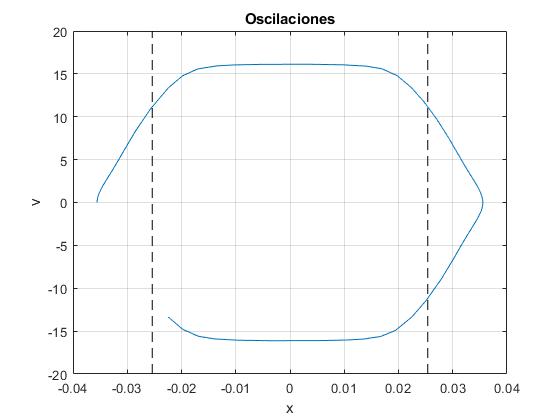
La variable te guarda la mitad del periodo, 9 milisegundos. El periodo o tiempo que tarda en completar una órbita en el espacio de las fases es 18 ms

>> te
te =    0.0090

Cañón magnético

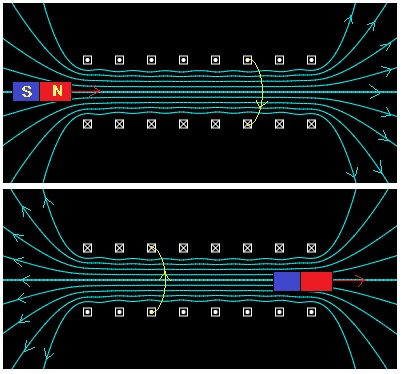
Supongamos ahora, que cuando el imán llega al centro del solenoide, la corriente se invierte. La fuerza que ejerce el campo magnético sobre el imán en el extremo derecho, tiene el mismo signo que su velocidad, el imán es de nuevo acelerado. La representación gráfica de la fuerza F(x) es

L=50.8/1000; %longitud del solenoide
a=3.9/1000; %radio solenoide, 
N=184;  %número de espiras
mu=0.455; %Am^2, momento magnético del imán
d=12.7/1000; %longitud del imán
I=200; %corriente, amperios

B0=4*pi*1e-7*N*I/L; %campo magnético constante
B=@(x) B0*((L/2-x)./sqrt((L/2-x).^2+a^2)+(L/2+x)./sqrt((L/2+x).^2+a^2))/2; %campo
F=@(x) mu*(B(x+d/2)-B(x-d/2))/d; %fuerza izquierda
FF=@(x) -mu*(B(x+d/2)-B(x-d/2))/d; %fuerza derecha
hold on
fplot(F,[-1*L,0]);
fplot(FF,[0,1*L]);

line([L/2,L/2],[0,FF(L/2)],'lineStyle','--', 'color','k')
line([-L/2,-L/2],[0,F(-L/2)],'lineStyle','--', 'color','k')%hold off
grid on
xlabel('x (m)')
ylabel('F (N)')
title('Fuerza')

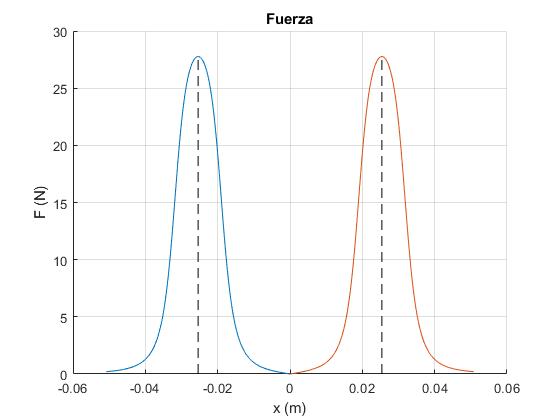
La descripción del movimiento del imán a lo largo del eje del solenoide es más compleja, la dividiremos en dos etapas:

Desde la posición inicial x₀ en reposo hasta el centro del solenoide (origen). Sobre el imán actúa una fuerza F(x) (a la izquierda en la figura). El imán llevará una velocidad v₁ y habrá tardado un tiempo t₁ en llegar al origen.
Sobre el imán actúa una fuerza -F(x) del mismo signo que su velocidad (a la derecha en la figura). El imán parte del origen x=0 con velocidad v₁ en el instante t₁ y llegará a la posición final x₂ con velocidad v₂ en el instante t₂

Para describir la primera etapa del movimiento del imán, definimos una función que detiene el proceso de integración cuando el imán llega al origen

function [value,isterminal,direction]=coilgun_invierte(t,x)
    value=x(1); %detecta el origen x=0
   isterminal=1;
    direction=1; 
end

Resolvemos la ecuación diferencial del movimiento del imán a lo largo del eje del solenoide

$\frac{d^{2} x}{d t^{2}} = \frac{F (x)}{m}$

por el procedimiento numérico ode23, con las siguientes condiciones iniciales: en el instante t=0, x=x₀, dx/dt=0. Parte del reposo en las proximidades del extremo izquierdo del solenoide. En este ejemplo, el imán parte de la posición x₀=-L=-50.8 mm

a=3.9/1000; %radio solenoide
L=50.8/1000; %longitud del solenoide
N=184;  %número de espiras
I=200; %corriente, amperios
mu=0.455; %Am^2, momento magnético del imán
m=0.003; %kg, masa del imán 
d=12.7/1000; %longitud del imán

tf=0.05; %tiempo final
x0=-1*L; %posición de partida
B0=4*pi*1e-7*N*I/L; %campo magnético uniforme
B=@(x) B0*((L/2-x)/sqrt((L/2-x)^2+a^2)+(L/2+x)/sqrt((L/2+x)^2+a^2))/2; 
F=@(x) mu*(B(x+d/2)-B(x-d/2))/d; %fuerza

%primera etapa
fg=@(t,x)[x(2);F(x(1))/m];
opts=odeset('events',@coilgun_invierte);
[t,x]=ode23(fg,[0,tf],[x0,0],opts);
plot(x(:,1),x(:,2))

line([L/2,L/2],[0,20],'lineStyle','--', 'color','k')
line([-L/2,-L/2],[0,20],'lineStyle','--', 'color','k')
grid on
xlabel('x')
ylabel('v')
title('Cañón magnético')

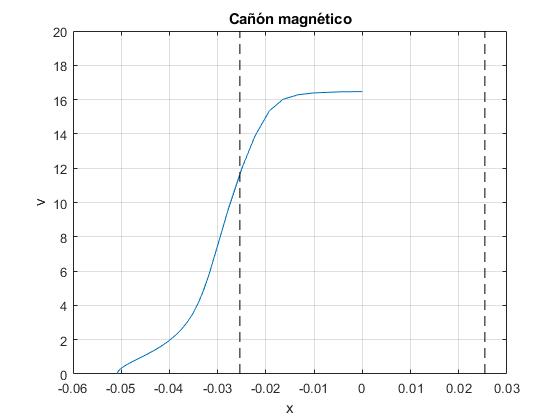
La velocidad en esta posición intermedia (origen) x₁=0 es v₁=16.5 m/s y el tiempo que tarda en llegar t₁=20.7 ms

>> x(end,1)
ans =     0
>> x(end,2)
ans =   16.4667
>> t(end)
ans =    0.0207

Añadimos el código que describe la segunda etapa. Para ello, definimos una función coilgun_stop que detiene el proceso de integración cuando el imán llega a la posición final x₂ que guarda la variable xf. Esta posición se le deberá pasar a dicha función

function [value,isterminal,direction]=coilgun_stop(t,x, xf)
    value=x(1)-xf; %detecta posición final xf
    isterminal=1;
    direction=1; 
end

Cambiamos el signo de la fuerza F(x)

$\frac{d^{2} x}{d t^{2}} = - \frac{F (x)}{m}$

integramos la ecuación diferencial por el procedimiento numérico ode23, con las siguientes condiciones iniciales: en el instante t₁ la posición del imán es el origen x₁=0, y su velocidad es v₁

....
%segunda etapa
opts=odeset('events',@(t,x) coilgun_stop(t,x,xf));
fg=@(t,x)[x(2);-F(x(1))/m];
[t,x]=ode23(fg,[t(end),tf],[0,x(end,2)], opts);
plot(x(:,1),x(:,2))
....

Unimos el código de las dos etapas en un único script

a=3.9/1000; %radio solenoide
L=50.8/1000; %longitud del solenoide
N=184;  %número de espiras
I=200; %corriente, amperios
mu=0.455; %Am^2, momento magnético del imán
m=0.003; %kg, masa del imán 
d=12.7/1000; %longitud del imán

tf=0.05; %tiempo final
x0=-1*L; %posición de partida
xf=1*L; %posición final
B0=4*pi*1e-7*N*I/L; %campo magnético uniforme
B=@(x) B0*((L/2-x)/sqrt((L/2-x)^2+a^2)+(L/2+x)/sqrt((L/2+x)^2+a^2))/2;
F=@(x) mu*(B(x+d/2)-B(x-d/2))/d; %fuerza

%primera etapa
fg=@(t,x)[x(2);F(x(1))/m];
opts=odeset('events',@coilgun_invierte);
[t,x]=ode23(fg,[0,tf],[x0,0],opts);
hold on
plot(x(:,1),x(:,2))
line([L/2,L/2],[0,20],'lineStyle','--', 'color','k')
line([-L/2,-L/2],[0,20],'lineStyle','--', 'color','k')%segunda etapa
opts=odeset('events',@(t,x) coilgun_stop(t,x,xf));
fg=@(t,x)[x(2);-F(x(1))/m];
[t,x]=ode23(fg,[t(end),tf],[0,x(end,2)], opts);
plot(x(:,1),x(:,2))
hold off

grid on
xlabel('x')
ylabel('v')
title('Cañón magnético')

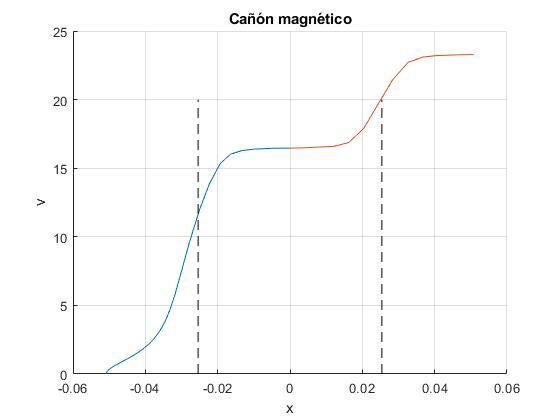
Llega a la posición final x₂=L=50.8 mm, en el instante t₂=23.3 ms, con velocidad v₂=23.3 m/s

>> t(end)
ans =    0.0233
>> x(end,1)
ans =    0.0508
>> x(end,2)
ans =   23.2818

Resumiendo: el imán tarda t₁=20.7 ms en desplazarse desde la posición inicial x₀=-L=-50.8 mm hasta el origen, x₁=0, alcanzando una velocidad v₁=16.47 m/s, que se mantiene casi constante en el interior del solenoide. Tarda un tiempo t₂-t₁=23.3-20.7=2.6 ms en alcanzar la posición final x₂=L=50.8 mm, con velocidad v₂=23.3 m/s

Relación entre velocidades

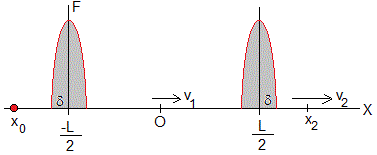
Vamos a establecer una relación entre las velocidades v₂ y v₁, cuando el punto de partida y llegada son simétricos, x₀=-x₂

El imán parte del reposo en la posición x₀, cuando llega a la posición x₁ (el origen) su velocidad es v₁. El trabajo de la fuerza F(x), que ejerce el campo magnético creado por el solenoide, es igual a la variación de energía cinética del imán

$\frac{1}{2} m v_{1}^{2} = \int_{- L / 2 - δ}^{- L / 2 + δ} F (x) d x$

El imán parte de la posición x₁ con velocidad v₁ y llega a la posición x₂ con velocidad v₂, el trabajo de la fuerza F(x) es igual a la variación de su energía cinética

$\frac{1}{2} m v_{2}^{2} - \frac{1}{2} m v_{1}^{2} = \int_{L / 2 - δ}^{L / 2 + δ} F (x) d x$

Si los dos trabajos (áreas) son iguales, llegamos a la relación

$\frac{v_{2}^{2}}{v_{1}^{2}} = 2, v_{2} = \sqrt{2} v_{1}$

En el ejemplo estudiado en este apartado, el imán parte de la posición inicial x₀=-L=-50.8 mm, en el origen, x₁=0, lleva una velocidad v₁=16.4667 m/s, en la posición final x₂=L=50.8 mm, lleva una velocidad v₂=23.2818 m/s

>> 23.2818/16.4667
ans =    1.4139
>> sqrt(2)
ans =    1.4142

En el siguiente ejemplo, el imán parte de la posición inicial x₀=-0.7L, en el origen, x₁=0, lleva una velocidad v₁=16.1122 m/s, en la posición final x₂=0.7L, lleva una velocidad v₂=22.8003 m/s

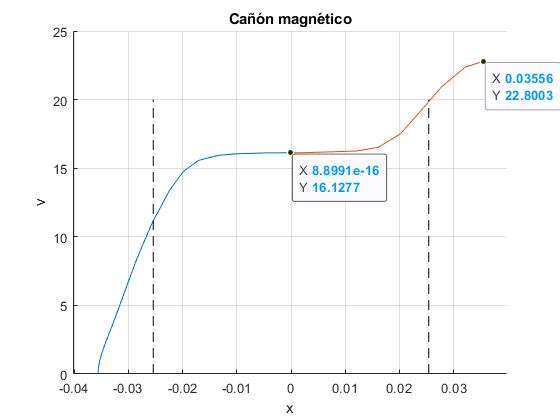
>> 22.8003/16.1122
ans =    1.4151

Al estar la posición inicial x₀ del imán más próximo al extremo izquierdo del solenoide, siente una fuerza atractiva más intensa, el tiempo total t₂=6.5 ms que tarda en llegar a la posición final se reduce notablemente

>> t(end)
ans =    0.0065

La intensidad de la corriente cambia con el tiempo

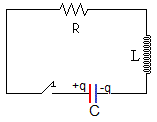
Cuando unimos los extremos del solenoide a un condensador de capacidad C=0.12 F, tenemos un circuito LCR. La resistencia del solenoide y los cables que le unen al condensador es R=0.24 Ω. La autoinducción del solenoide de longitud L=50.8 mm y radio a=3.9 mm es

$\frac{μ_{0} N^{2} (π a^{2})}{L}$

>> 4*pi*1e-7*N^2*pi*a^2/L
ans =   4.0019e-05

40 μH, es una autoinducción muy pequeña, por lo que en la práctica podemos considerar que el condensador se descarga a través de una resistencia, constituye un circuito RC

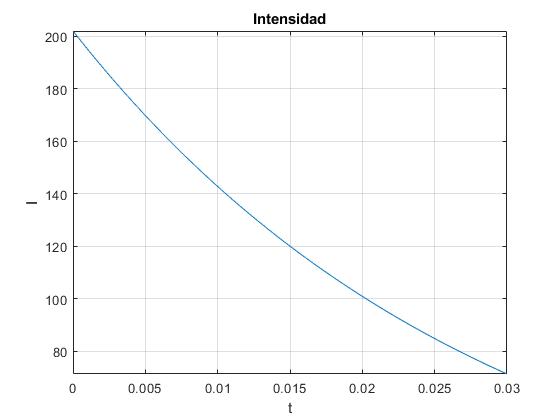
$\begin{array}{l} I (t) = \frac{V_{0}}{R} \exp (- \frac{t}{R C}) \\ V (t) = V_{0} \exp (- \frac{t}{R C}) \end{array}$

La intensidad disminuye exponencialmente con el tiempo. Representamos la inetensidad I en función del tiempo t hasta 30 ms

C=0.12; %faradios, capacidad
R=0.24; %ohmios, resistencia
V0=48.5; %voltios, 
I=@(t) V0*exp(-t/(R*C))/R;
fplot(I,[0,0.03]); %40 ms
grid on
xlabel('t')
ylabel('I')
title('Intensidad')

Modificamos el script que describe las dos etapas del movimiento del imán para incluir una intensidad que cambia con el tiempo. La ecuación diferencial del movimiento es de la forma

$\frac{d^{2} x}{d t^{2}} = \frac{F (t, x)}{m}$

La fuerza sobre el imán F(t,x), es una función de su posición x y del tiempo t

En el siguiente ejemplo, el imán parte de la posición inicial x₀=-0.7L y llega a la posición final x₂=0.7L. En la figura, se proporcionan los datos de las velocidades

a=3.9/1000; %radio solenoide
L=50.8/1000; %longitud del solenoide
N=184;  %número de espiras
mu=0.455; %Am^2, momento magnético del imán
m=0.003; %kg, masa del imán 
d=12.7/1000; %longitud del imán
C=0.12; %faradios, capacidad
R=0.24; %ohmios, resistencia
V0=48.5; %voltios, 

tf=0.1; %tiempo final
x0=-0.7*L; %posición de partida
xf=0.7*L; %posición final
B0=@(t) 4*pi*1e-7*N*V0*exp(-t/(R*C))/(L*R); %campo magnético uniforme
B=@(x,t) B0(t)*((L/2-x)/sqrt((L/2-x)^2+a^2)+(L/2+x)/sqrt((L/2+x)^2+a^2))/2; %campo
F=@(x,t) mu*(B(x+d/2,t)-B(x-d/2,t))/d; %fuerza

%primera etapa
fg=@(t,x)[x(2);F(x(1),t)/m];
opts=odeset('events',@coilgun_invierte);
[t,x]=ode23(fg,[0,tf],[x0,0],opts);
hold on
plot(x(:,1),x(:,2))
line([L/2,L/2],[0,20],'lineStyle','--', 'color','k')
line([-L/2,-L/2],[0,20],'lineStyle','--', 'color','k')

%segunda etapa
opts=odeset('events',@(t,x) coilgun_stop(t,x,xf));
fg=@(t,x)[x(2);-F(x(1),t)/m];
[t,x]=ode23(fg,[t(end),tf],[0,x(end,2)], opts);
plot(x(:,1),x(:,2))

hold off
grid on
xlabel('x')
ylabel('v')
title('Cañón magnético')

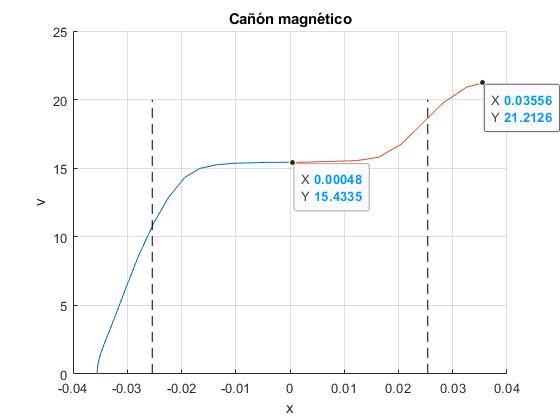
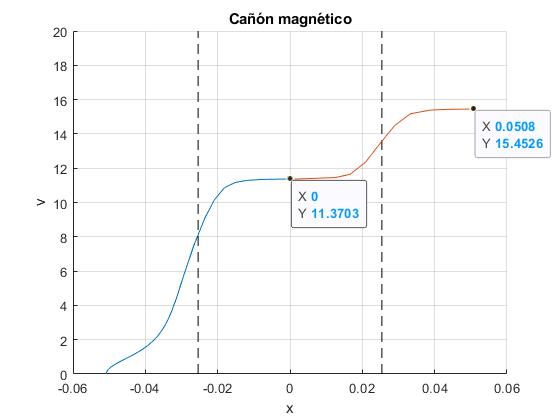
En el siguiente ejemplo, el imán parte de la posición inicial x₀=-L y llega a la posición final x₂=L. En la figura, se proporcionan los datos de las velocidades. El imán pasa mucho tiempo desplazándose desde la posición inicial, ya que la fuerza de atracción es muy pequeña, la intensidad disminuye rápidamente con el tiempo, así también lo hace el campo creado por el solenoide y la fuerza sobre el imán. Obtenemos, por tanto, una velocidad final más pequeña, tardando un tiempo mucho más grande en alcanzarla, 28.1 ms frente a 6.7 ms

Optimización

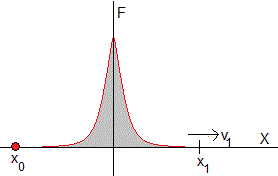
Supongamos una fuerza que varía con la posición F(x). Una partícula de masa m parte del reposo en la posición x₀ y llega a la posición x₁ con velocidad v₁, el trabajo de la fuerza F(x) entre x₀ y x₁ se invierte en incrementar la energía cinética de la partícula. La velocidad v₁ será más grande cuando x₀ y x₁ están lo más alejados posible.

$\frac{1}{2} m v_{1}^{2} = \int_{x_{0}}^{x_{1}} F (x) d x$

Ahora bien, si x₀ está lejos del origen, la fuerza F(x) será muy pequeña por lo que tardará mucho tiempo en desplazarse

Si x₁ está lejos del origen, la partícula, una vez que ha alcanzado una velocidad próxima a la máxima (después de pasar por el origen), se desplazará a velocidad casi constante.

La optimización se refiere al compromiso entre una velocidad final que sea la más alta posible con un tiempo empleado en alcanzarla que sea razonable

Como se ha puesto de manifiesto en el apartado anterior, si elegimos una posición inicial alejada del extremo izquierdo del solenoide, el imán siente una fuerza muy pequeño, pasa mucho tiempo desplazándose hacia el origen, la intensidad disminuye rápidamente con el tiempo y del mismo modo, lo hace la fuerza, por lo que la velocidad final sería pequeña y el tiempo empleado en alcanzarla muy grande. El lector deberá ensayar la máxima velocidad final con la mejor eficiencia, el cociente

$η = \frac{\frac{1}{2} m v^{2}}{\frac{1}{2} C (V_{0}^{2} - V^{2})}$

El numerador es la energía cinética final del proyectil, el denominador es la energía eléctrica consumida. V₀=48.5 V es la diferencial de potencial inicial y V es la diferencia de potencial final en el condensador. Tenemos que buscar un compromiso entre la velocidad final más alta posible con el menor tiempo que tarde en alcanzar la posición final.

Actividades

Se introduce

La posición inicial de partida del imán en reposo, a la izquierda del origen, en unidades de la longitud L del imán, en el control titulado Posición inicial. -0.5L es el extremo izquierdo del solenoide
La posición final de llegada del imán, a la derecha del origen, en unidades de la longitud L del imán, en el control titulado Posición final. 0.5L es el extremo derecho del solenoide

Los siguientes parámetros se han fijado en el programa interactivo

El radio del solenoide, a=3.9 mm
El número de espiras, N=184.
La longitud del solenoide, L=50.8 mm
La longitud del imán, d=12.7 mm
La radio del imán, r=3.175 mm
El momento magnético del imán, μ=0.455 A·m²
La masa del imán, m=0.003 kg
La capacidad del condensador, C=0.12 F
La diferencia de potencial inicial, V₀=48.5 V
La resistencia total del solenoide y los cables de conexión, R=0.24 Ω

Se resuelve la ecuación diferencial del movimiento del imán a lo largo del eje del solenoide por el procedimiento de Runge-Kutta dando unos resultados similares a los obtenidos con MATLAB

Se representa la intensidad de la corriente que circula por el solenoide, se invierte cuando el imán pasa por el origen y se hace cero cuando el imán llega a la posición final. A partir de esta posición el imán se mueve con velocidad constante.

Posición inicial ·L: final ·L:

Referencias

Joshua Zhou, Takyiu Liu. Physical analysis and optimization of electromagnetic coilgun launch systems. Am. J. Phys. 87, (11) November 2019, pp. 894-900