Fuerza sobre un circuito cerrado por el que circula una corriente
Vamos a calcular las fuerzas que actúan sobre un circuito cerrado que transporta una corriente constante y que está situado en un campo magnético uniforme perpendicular al plano que contiene el circuito.
Circuito formada por una porción semicircular de radio R y su diámetro
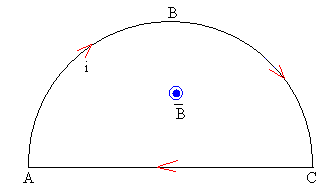
Supondremos que el campo magnético es uniforme perpendicular al plano del circuito y apunta hacia el lector. La corriente constante de intensidad i circula en el sentido de las agujas del reloj
La fuerza que ejerce el campo magnético sobre una porción dl de una corriente es
-
Fuerza sobre la porción rectilínea AC
-
por módulo, dF=i(1·B·sin90º)·dx=iB·dx
-
dirección, perpendicular al plano determinado por y , el eje Y
-
sentido, positivo.
-
por módulo,
-
dirección, el eje Y
-
sentido, positivo
-
Fuerza sobre la porción semicircular ABC
-
por módulo, dF=i(1·B·sin90º)·dl=iBR·dθ
-
dirección, perpendicular al plano determinado por y , radial
-
sentido, hacia el centro
-
La fuerza resultante sobre el circuito ABCA es nula
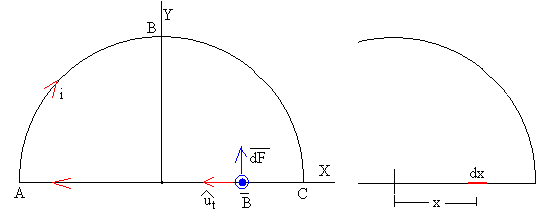
La fuerza que ejerce el campo magnético sobre el elemento de corriente de longitud dx tiene:
La fuerza sobre todos los elementos de corriente tienen la misma dirección y sentido. La resultante tiene
En forma vectorial,
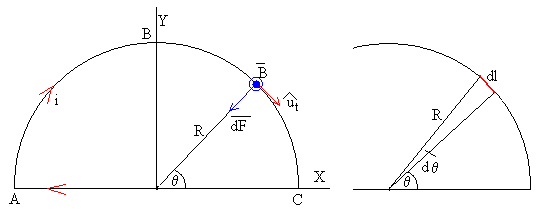
La fuerza que ejerce el campo magnético sobre el elemento de corriente de longitud dl=R·dθ tiene:
Hallamos las componentes rectangulares de la fuerza
dFx=-dF·cosθ=-iBR·cosθ
·dθ
dFy=-dF·sinθ=-iBR·sinθ
·dθ
Calculamos las componentes de la fuerza resultante.
Por simetría, la componente Fx debe ser nula, sin necesidad de calcular la integral
En forma vectorial,
Circuito cerrado formado por porciones rectas y semicirculares
Consideremos el circuito ABCDA, recorrido en sentido horario por una corriente de intensidad i. Vamos a calcular la fuerza que ejerce el campo magnético , uniforme, perpendicular al plano del circuito y dirigido hacia el lector sobre cada una de las porciones del circuito.
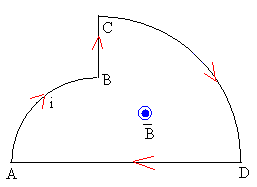
-
La porción AB, es un cuarto de circunferencia de radio r.
-
La porción BC es un segmento rectilíneo vertical de longitud R-r
-
por módulo, FBC=iB(R-r)
-
dirección, perpendicular al plano determinado por y , eje X
-
sentido, positivo
-
La porción CD, es un cuarto de circunferencia de radio R.
-
La porción DA es un segmento rectilíneo vertical de longitud R+r
-
por módulo, FDA=iB(R+r)
-
dirección, perpendicular al plano determinado por y , eje Y
-
sentido, positivo
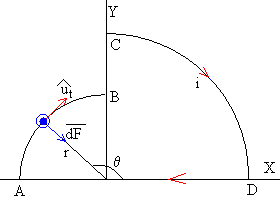
En el apartado anterior, calculamos la fuerza sobre un elemento de corriente de longitud dl=r·dθ y las componentes de dicha fuerza. Calculamos ahora, las componentes de la fuerza resultante
En forma vectorial,
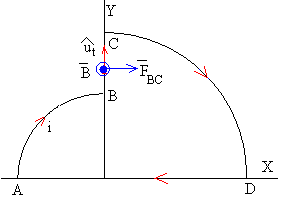
La fuerza que ejerce el campo magnético sobre esta porción de corriente tiene
En forma vectorial,
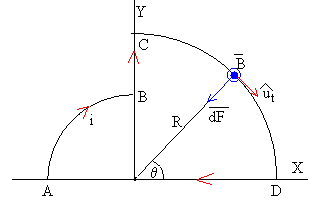
En el apartado anterior, calculamos la fuerza sobre un elemento de corriente de longitud dl=R·dθ y las componentes de dicha fuerza
Calculamos ahora, las componentes de la fuerza resultante
En forma vectorial,
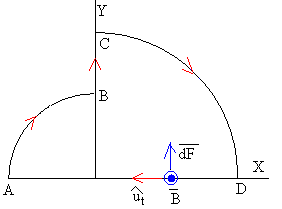
La fuerza que ejerce el campo magnético sobre esta porción de corriente tiene
En forma vectorial,
La fuerza resultante es
Circuito cerrado de forma cualesquiera
En general, la fuerza que ejerce el campo magnético sobre una corriente cerrada es nula.
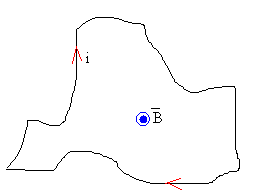
La integral entre paréntesis es nula, ya que la suma de todos los vectores desplazamiento infinitesimales de un camino cerrado es nula, salimos de un punto y regresamos al mismo punto, no hay un desplazamiento neto.
Así pues, hemos comprobado que la resultante de las fuerzas que ejerce el campo magnético uniforme sobre un circuito cerrado de forma cualesquiera, es nula. El campo magnético es perpendicular al plano que contiene el circuito cerrado, aunque no tiene que serlo, necesariamente.
Referencias
A. Casaca, J. P. Silva Magnetic Forces Acting on Rigid Current-Carrying Wires Placed in Uniform magnetic Field. The Physics Teacher, Vol. 42, March 2004, pp. 161-163

