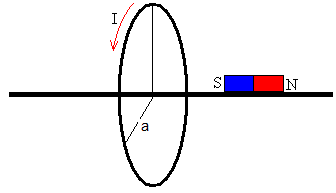
En una primera aproximación, ignoraremos el efecto del tamaño finito del imán.

Consideremos una bobina muy estrecha de N espiras del mismo radio a. El campo producido por dicha bobina en un punto P del eje de la bobina situado a una distancia x de su centro es

${\displaystyle B(x)=N\frac{{\mu }_0{R}^{2}I}{2{\left(\sqrt{a^2+x^2}\right)}^3}}$

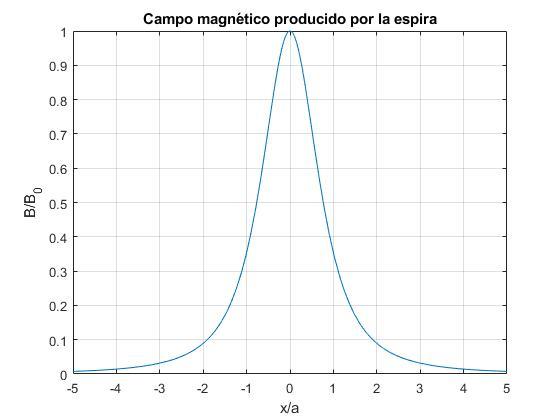
El campo magnético tiene la forma de una función simétrica respecto del eje Y que se aproxima rápidamente a cero al alejarnos del origen, tal como se aprecia en la figura

${\displaystyle f(x)=\frac{1}{{\left(1+x^2/a^2\right)}^{3/2}}}$

B=@(x) 1./(1+x.^2).^(3/2);
fplot(B,[-5,5]);
grid on
xlabel('x/a')
ylabel('B/B_0')
title('Campo magnético producido por la espira')

Supongamos que un imán de momento magnético $\overrightarrow{\mu }$ está situado en dicho punto P, de modo que el vector $\overrightarrow{B}$ y el vector $\overrightarrow{\mu }$ son paralelos.

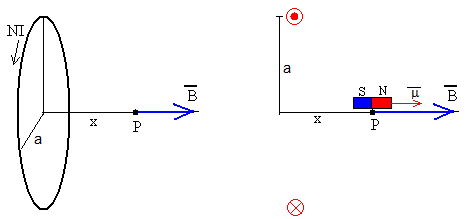
La energía potencial del imán será

${\displaystyle E_p(x)=-\overrightarrow{\mu }·\overrightarrow{B}=-N\frac{{\mu }_0{R}^{2}I}{2{(\sqrt{a^2+x^2})}^3}\mu }$

Si la oscilación tiene lugar en las proximidades del centro de la bobina, de modo que x<<a, el movimiento del imán es aproximadamente armónico.

Desarrollando E_p(x) en serie alrededor de x=0, obtenemos

${\displaystyle E_p(x)=-\frac{{\mu }_{0}IN\mu }{2a}+\frac{3{\mu }_{0}IN\mu }{4a}\frac{x^2}{a^2}-\frac{15{\mu }_{0}IN\mu }{16a}\frac{x^4}{a^4}+\mathrm{...}}$

>> syms x a;
>> taylor(1/(1+x^2/a^2)^(3/2),x)
ans =(15*x^4)/(8*a^4) - (3*x^2)/(2*a^2) + 1

El primer término, no tiene influencia en el movimiento, ya que la energía potencial está definida salvo una constante aditiva que nos sirve para establecer el origen de la energía potencial.

El segundo término, corresponde a la energía potencial de un oscilador armónico. Para una partícula de masa m que describe un M.A.S. de frecuencia angular ω, la energía potencial se escribe

${\displaystyle E_p(x)=\frac{1}{2}m{\omega }^2{x}^2+\text{cte}}$

Despreciando los términos de orden superior a x² en el desarrollo en serie, obtenemos la frecuencia angular ω,

${\displaystyle {\omega }^2=\frac{3{\mu }_0\mu IN}{2m{a}^3}}$

La ecuación de un M.A.S se escribe

x=A·sin(ωt+φ)
v=Aω·cos(ωt+φ)

Si en el instante inicial la partícula parte de la posición x=A con velocidad v=0. La ecuación del movimiento será

x=A·sin(ωt+π/2)=A·cos(ωt)

Movimiento oscilatorio del imán

En una segunda aproximación, consideraremos el efecto de la longitud del imán, suponiendo que las otras dimensiones (ancho y alto si el imán tiene forma de paralepípedo, radio si tiene forma cilíndrica) son pequeñas para considerar el campo magnético aproximadamente uniforme en la sección trasversal del imán.

Si la amplitud de la oscilación no es pequeña comparada con el radio a de la bobina (como hemos supuesto en el apartado anterior), el movimiento del imán deja de ser armónico simple (M.A.S.).

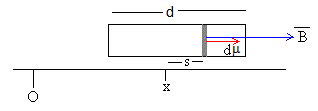
Consideraremos que el imán está formado por una distribución continua de dipolos (en color oscuro en la figura) de momento dipolar magnético dμ=(μ/d)ds.

Calculamos la energía de esta distribución continua en el campo magnético B producido por una bobina formada por N espiras apretadas del mismo radio a, por la que circula una corriente de intensidad I.

dE_p=-B(x+s)·dμ

donde B(x+s) es el campo producido por la bobina en la posición x+s que ocupa el dipolo puntual de longitud ds. Tal como se ve en la figura

• s es la distancia entre el punto medio del imán y la posición del dipolo puntual dm
• x es la distancia del punto medio del imán al centro de la bobina.

La energía potencial total del imán será

${\displaystyle E_p(x)=-\frac{\mu }{d}{\displaystyle \underset{-d/2}{\overset{d/2}{\int }}B(x+s)ds}}$

Dada la energía potencial, calculamos la fuerza que ejerce el campo magnético sobre el imán

${\displaystyle \begin{array}{l}F(x)=-\frac{d{E}_p(x)}{dx}=\frac{\mu }{d}{\displaystyle \underset{-d/2}{\overset{d/2}{\int }}\frac{dB(x+s)}{dx}}ds=\frac{\mu }{d}{\displaystyle \underset{-d/2}{\overset{d/2}{\int }}\frac{dB(x+s)}{ds}}ds\\ F(x)=\frac{\mu }{d}\left(B(x+\frac{d}{2})-B(x-\frac{d}{2})\right)\end{array}}$

Ejemplo:

• El radio de la espira, a=50 cm =0.5 m
• La intensidad de la corriente, I=2 A
• El número de espiras, N=150.
• La longitud del imán, d=7 cm=0.07 m
• El momento magnético del imán, μ=3.5 A·m²

d=0.07; %longitud del imán en m
N=150; %número de espiras
I=2.0; %intensidad de la corriente
a=0.5; %radio espiras
mu=3.5; %momento magnético

B0=N*4*pi*1e-7/(2*a); %campo magnético en el centro de la espira
B=@(x) B0./(1+x.^2).^(3/2);
F=@(x) mu*(B(x+d/2)-B(x-d/2))/d; %fuerza sobre el imán
fplot(F,[-5*a,5*a]);
grid on
xlabel('x')
ylabel('F')
title('Fuerza sobre el imán')

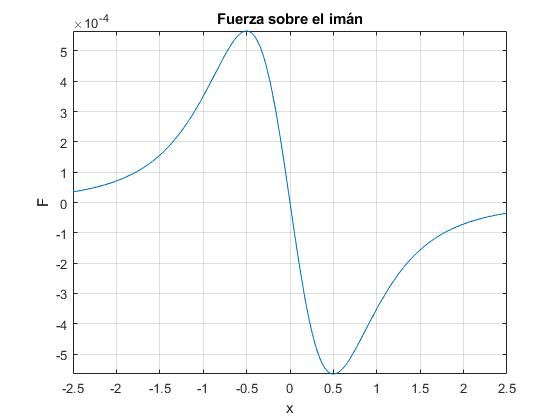
Conocida la fuerza F(x) y la masa m del imán. La ecuación del movimiento se escribe

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=\frac{\mu }{d}\left(B(x+\frac{d}{2})-B(x-\frac{d}{2})\right)\\ B(x)=N\frac{{\mu }_0{a}^{2}I}{2{\left(\sqrt{a^2+x^2}\right)}^3}\end{array}}$

d=0.07; %longitud del imán en m
N=150; %número de espiras
m=0.25; %masa 
I=2.0; %intensidad
a=0.5; %radio espiras
mu=3.5; %momento magnético

w0=sqrt(3*4*pi*1e-7*I*N*mu/(2*m*a^3));	%frecuencia angular	
B=@(x) N*(4*pi*1e-7)*a^2*I/(2*sqrt(a^2+x^2)^3); %campo magnético
x0=[0.3,0];  %[posición inical en cm, velocidad inicial]
tspan=[0 10*2*pi/w0;];  %diez periodos

%solución numérica
f=@(t,x) [x(2);mu*(B(x(1)+d/2)-B(x(1)-d/2))/(m*d)]; 
[t,x]=ode45(f,tspan,x0);

plot(t,x(:,1), 'b')
xlabel('t')
ylabel('x');
title('Oscilaciones longitudinales del imán')
grid on

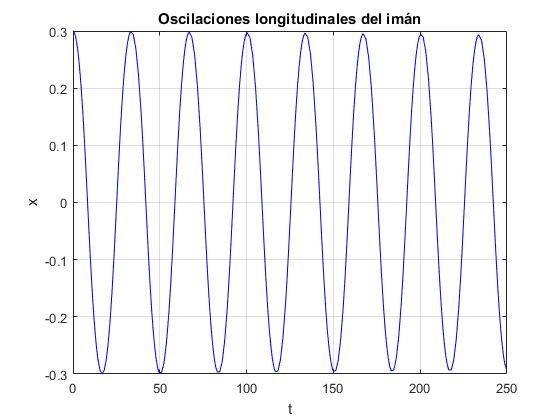
Actividades

Se introducen

• El momento magnético μ del imán en A·m², en el control de edición titulado M. magnético.
• Se introduce la longitud d del imán en cm, en en el control titulado Longitud imán.
• La masa del imán está fijada en el programa interactivo en el valor m=250 g  
• El radio a de la las espiras de la bobina en cm, en el control titulado Radio espira
• La intensidad I de la corriente que circula por las espiras de la bobina en A, en el control titulado Intensidad.
• El número de espiras se ha fijado en el programa interactivo en N=150.
• La posición inicial del imán en cm, la velocidad inicial es cero, en el control titulado Posición inicial.

Se pulsa el botón titulado Nuevo

En la parte izquierda, observamos el movimiento del imán a lo largo del eje de la bobina.

En la parte derecha, observamos la representación gráfica de la energía potencial del imán E_p(x). La ordenada de la recta horizontal de color negro representa la energía total, la energía potencial (en color azul) y la diferencia, en color rojo, es la energía cinética. Mediante una flecha horizontal, se señala la fuerza F(x) sobre el imán. La fuerza es nula en el mínimo de la curva de la energía potencial. Es positiva para x<0 (la pendiente de la curva es negativa) y es negativa para x>0 (la pendiente es positiva).

Se trata de un ejemplo más de oscilación no armónica, que se puede aproximar a un M.A.S. cuando la amplitud de la oscilación es pequeña, es decir, en las proximidades del mínimo de la energía potencial.

Ejemplo:

• El radio de la espira, a=50 cm =0.5 m
• La intensidad de la corriente, I=2 A
• El número de espiras, N=150.
• El momento magnético del imán, μ=3.5 A·m²
• La masa del imán, m=250 g=0.25 kg.

La frecuencia angular y el periodo P de las oscilaciones armónicas es

${\displaystyle {\omega }^2=\frac{3{\mu }_{0}IN\mu }{2m{a}^3}=\frac{3·4\pi ·{10}^{-7}·2·150·3.5}{2·0.25·{0.5}^3}P=\frac{2\pi }{\omega }=24.97\text{s}}$

Medimos el tiempo de varias oscilaciones completas y determinamos el periodo P o la frecuencia angular ω de la oscilación. Para medir el periodo utilizamos los botones pausa || y paso a paso >|

Referencias

Bisquert J. Hurtado E., Mafé S., Pina J. Oscillations of a dipole in a magnetic field: An experiment. Am. J. Phys. 58 (9) September 1990, pp. 838-843.