Actualmente, los galvanómetros utilizados son del tipo D’Arsonval de cuadro móvil formado por un conjunto de espiras que pueden girar alrededor de un eje. Las espiras forman una pequeña bobina rectangular montada sobre un cilindro de hierro dulce.

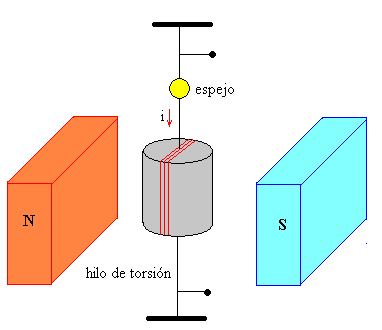
Las espiras están situadas entre los polos de un potente imán. El imán está diseñado de modo que el campo magnético en la región en que las espiras giran tiene dirección radial. El eje de rotación puede ser vertical con las espiras suspendidas de un hilo de torsión, o bien, el eje de rotación puede ser horizontal unido a un muelle helicoidal.

Fuerzas y momento sobre las espiras

Calcularemos la fuerza que ejerce un campo magnético radial sobre cada uno de los lados de una espira rectangular.

Ya hemos deducido la expresión de la fuerza que ejerce un campo magnético sobre una porción L de corriente rectilínea.

${\displaystyle \overrightarrow{F_m}=i{\widehat{u}}_t\times \overrightarrow{B}·L}$

donde, ${\widehat{u}}_t$ es un vector unitario que nos señala la dirección y el sentido en el que se mueven los portadores de carga positivos.

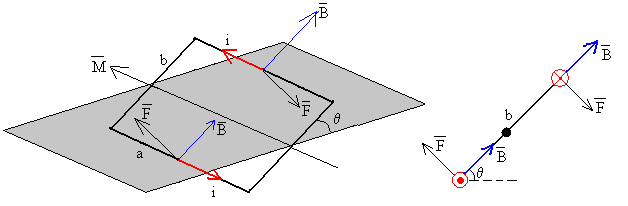
La fuerza F sobre cada uno de los lados de longitud a, está señalada en la figura y su módulo vale

F=i·1·B·a·sin90º=iBa.

Como vimos en la página anterior la fuerza que ejerce el campo magnético sobre cada uno de los lados de longitud b, no afecta al movimiento de la espira.

El momento de las fuerzas sobre la espira respecto del eje de rotación es

M=2F(b/2)=i·ab·B

Si la bobina está formada por N espiras iguales, el momento total es

M=Ni·S·B

Siendo S=ab el área de cada una de las espiras.

Medida de la constante K de un galvanómetro

Como hemos visto al estudiar el péndulo de torsión. El momento que ejerce el campo magnético hace girar las espiras un ángulo θ, tal que

Ni·S·B=k·θ

Siendo k la constante de torsión del hilo o del muelle helicoidal.

Definimos la constante K del galvanómetro como el cociente entre la intensidad y el ángulo girado.

${\displaystyle \frac{i}{\theta }=\frac{k}{NSB}=K}$

La constante K depende solamente de las características del galvanómetro (campo magnético B entre las piezas polares del imán, constante de torsión del hilo k, número de espiras N de la bobina y área S de cada una de las espiras).

Para calibrar el galvanómetro, se toman medidas del ángulo de desviación θ , en función de corrientes i conocidas y se traza la recta que mejor ajusta mediante el procedimiento de mínimos cuadrados. La pendiente de dicha recta es la constante K del galvanómetro.

Actividades

En el programa interactivo que viene más abajo, realizamos una experiencia que nos permite medir la constante K de un galvanómetro, a la vez que realizar un ejercicio sobre las fuerzas y el momento que ejerce un campo magnético sobre una espira.

• Cuando se carga la página en el navegador, el programa interactivo genera de forma aleatoria los valores del campo magnético B y la constante k de torsión del hilo.
• Introducimos el valor de la corriente i (en microamperios) positiva o negativa en el control titulado Intensidad.

Se pulsa el botón titulado Nuevo

El indicador del galvanómetro nos señala sobre una escala graduada el ángulo girado por las espiras.

Si el ángulo girado es mayor, en valor absoluto, que 60º, supondremos que las espiras salen de la región en la que hay un campo magnético radial, y el mensaje Reduce la intensidad nos lo notifica. Deberemos entonces, disminuir la intensidad de la corriente que circula por el galvanómetro.

Ejemplo

Para una intensidad de 4 mA la aguja indicadora del galvanómetro se ha desviado 26.4º.

${\displaystyle K=\frac{0.004}{26.4·\pi /180}=8.67·{10}^{-3}\text{A/rad}}$

En la parte superior, se muestran sus características

• Número de espiras N=50
• Área de cada espira S=6 cm²
• Intensidad del campo magnético B=65 gauss

La constante k de torsión del hilo o del muelle helicoidal valdrá

k=K·NS·B=8.67·10^-3·50·6·10^-4·65·10^-4=1.69·10^-6 N·m

El momento de las fuerzas que ejerce el campo magnético sobre la espira vale

M=N·iS·B=50·0.004·6·10^-4·65·10^-4=7.8·10^-7 N·m

El momento que ejerce el hilo cuando ha girado un ángulo θ=26.4º es

M=k·θ=1.69·10^-6·26.4·π/180=7.8·10^-7 N·m

Oscilaciones libres

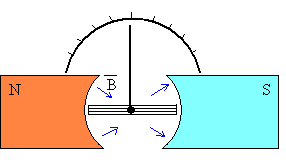
En muchos casos deseamos medir la carga que fluye a través del galvanómetro durante un corto intervalo de tiempo. El galvanómetro que se usa para realizar tales medidas se denomina balístico.

El campo magnético ejerce un par de fuerzas F sobre la corriente que circula por las espiras durante dicho intervalo de tiempo.

El momento de dichas fuerzas respecto del eje de rotación como hemos deducido en la sección anterior vale

M=N·iS·B

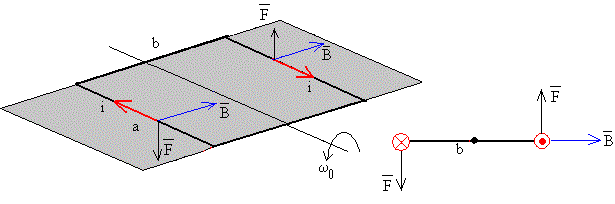
La corriente i decrece rápidamente con el tiempo produciendo un impulso angular

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}M·dt}=NSB{\displaystyle \underset{0}{\overset{\infty }{\int }}i·dt}=NSB·q}$

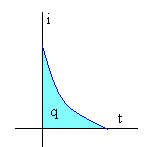
donde q es la carga total que pasa por el galvanómetro. Aunque los límites de integración se toman entre 0 e ∞, en la práctica casi toda la carga pasa a través del galvanómetro en la una fracción de segundo.

En la figura, la carga q es el área bajo la curva intensidad i en función del tiempo t.

Durante este pequeño intervalo de tiempo, el galvanómetro apenas ha girado, debido a que su momento de inercia I es grande. Sin embargo, ha adquirido una velocidad angular ω , ya que el impulso angular modifica la velocidad angular de un cuerpo en rotación.

${\displaystyle {\displaystyle \underset{0}{\overset{t}{\int }}M·dt}=I\omega -I{\omega }_0}$

Como la velocidad angular inicial es nula ω₀=0, tendremos que

NSB·q=Iω

Por tanto, ω es la velocidad angular inicial que adquiere el galvanómetro justamente después de que haya pasado toda la carga q.

Oscilaciones libres

La energía cinética inicial de rotación Iω²/2 se convierte en energía potencial elástica cuando el indicador gira hasta el ángulo de máximo desplazamiento θ₀.

${\displaystyle \frac{1}{2}I{\omega }^2=\frac{1}{2}k{\theta }_0^2\omega ={\theta }_{\text{0}}\sqrt{\frac{k}{I}}}$

Siendo k la constante de torsión del hilo o del muelle helicoidal.

Una vez que alcanza la máxima desviación θ₀ el indicador retorna a la posición de partida con velocidad angular -ω , pero en sentido opuesto, a continuación vuelve a alcanza la máxima desviación –θ₀ pero en el lado contrario de la escala graduada, y regresa a la posición de partida con velocidad ω. Tenemos un sistema semejante a un péndulo de torsión, cuyo periodo de oscilación ya hemos deducido. 

${\displaystyle P=2\pi \sqrt{\frac{I}{k}}}$

Conocida la constante K del galvanómetro, medimos la máxima desviación θ₀ del indicador del galvanómetro y el periodo P de sus oscilaciones. A partir de estos datos, despejamos la carga q que pasa a través del galvanómetro en un intervalo de tiempo muy corto comparado con el periodo P de oscilación del galvanómetro.

${\displaystyle q=\frac{K{\theta }_{0}P}{2\pi }}$

Actividades

Cada vez que se carga la página el programa interactivo genera números aleatorios que representan a la constante de torsión k del hilo o del muelle helicoidal, del momento de inercia I del galvanómetro y del campo magnético B creado por el imán.

El programa no permite definir el perfil de la corriente que circula por el galvanómetro durante un pequeño intervalo de tiempo. Si permite en cambio, introducir el efecto, es decir, la velocidad inicial de rotación ω que adquiere el galvanómetro balístico tras el paso de dicha corriente.

El programa interactivo nos suministra el dato de la constante del galvanómetro K, que supondremos que habrá sido medida por el procedimiento estático seguido en la sección anterior.

Con este dato y midiendo la amplitud de la oscilación θ₀ y su periodo P, obtenemos la carga q que ha pasado por el galvanómetro.

Ejemplo:

• Sea la constante del galvanómetro K=0.0077 A/rad
• Introducimos la velocidad angular adquirida por el cuadro del galvanómetro tras el paso de la corriente, ω =4 rad/s
• Medimos la amplitud de la oscilación θ₀=28º
• Medimos el tiempo que tarda en describir cinco oscilaciones completas t=3.74 s. El periodo es entonces P=3.75/5=0.75 s.

Calculamos la carga q

${\displaystyle q=\frac{0.0077·(28\pi /180)·0.75}{2\pi }=4.49·{10}^{-4}\text{C}}$

1. Se introduce el valor de la velocidad angular inicial, en el control titulado Velocidad angular
2. Se pulsa el botón titulado Nuevo
3. Se mide la máxima desviación y el periodo de varias oscilaciones con ayuda de los botones pausa || y paso a paso >|