En la página “Movimiento de rodar sobre un plano inclinado” hemos estudiado el movimiento de un cilindro que baja rodando por un plano inclinado.

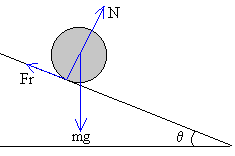
Las fuerzas que actúan sobre el cilindro son:

• el peso mg
• la reacción del plano inclinado N
• la fuerza de rozamiento F_r en el punto de contacto entre la rueda y el plano.

Las ecuaciones del movimiento serán

• Movimiento de traslación del c.m.

mg·sinθ -F_r=ma_c

• Movimiento de rotación alrededor de un eje que pasa por el c.m.

F_rR=I_cα

• Relación entre el movimiento de traslación y rotación (rueda sin deslizar)

a_c=α R

Para un cilindro de momento de inercia I_c=mR²/2, la aceleración del centro de masa es

${\displaystyle a_c=\frac{2}{3}g\sin \theta }$

Movimiento del cilindro con un imán en su interior

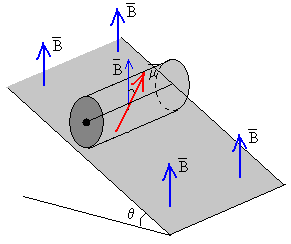
Consideremos ahora un cilindro situado sobre un plano inclinado con un imán de momento magnético $\overrightarrow{\mu }$ en su interior. En la región en la que se mueve el cilindro existe un campo magnético  uniforme $\overrightarrow{B}$, que apunta verticalmente hacia arriba, producido por un par de bobinas de Helmholtz.

Supongamos que en el instante inicial, el cilindro se encuentra en el origen, el campo magnético $\overrightarrow{B}$ y el momento magnético del imán $\overrightarrow{\mu }$ forman un ángulo π/2. El cilindro rueda sobre el plano inclinado, y en el instante t el ángulo que forma el momento magnético con la dirección de $\overrightarrow{B}$ es φ+π/2. El campo magnético $\overrightarrow{B}$ ejerce un momento sobre el imán, dado por el producto vectorial $\overrightarrow{M}=\overrightarrow{\mu }\times \overrightarrow{B}$

• El módulo del producto vectorial es M=μB·sin(φ+π/2)= μB·cosφ
• La dirección a lo largo del eje de rotación
• El sentido se determina aplicando la regla del sacacorchos

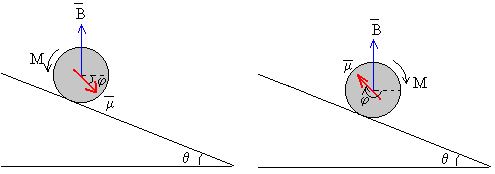
El momento $\overrightarrow{M}$ no es constante, sino que su módulo y su sentido cambian a medida que el cilindro rueda a lo largo del plano inclinado tal como se muestra en la figura

Las ecuaciones del movimiento se escriben ahora

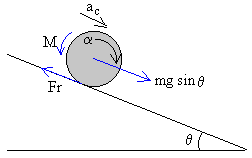
• Movimiento de traslación del c.m.

mg·sinθ -F_r=ma_c

• Movimiento de rotación alrededor de un eje que pasa por el c.m.

F_rR-μ·B·cosφ=I_cα

• Relación entre el movimiento de traslación y rotación (rueda sin deslizar)

a_c=α R

Despejamos la aceleración del centro de masas a_c, o mejor, el producto ma_c

${\displaystyle m{a}_c=\frac{2}{3}mg\sin \theta -\frac{2}{3}\frac{\mu B}{R}\text{cos}\phi }$

Cuando el cilindro rueda sin deslizar, su c.m. se desplaza una distancia x a lo largo del plano inclinado. El ángulo girado por el momento magnético del imán $\overrightarrow{\mu }$ respecto de su dirección inicial es φ=x/R, siendo R el radio del cilindro, tal como se muestra en la figura.

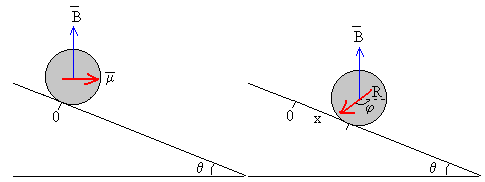
La aceleración del c.m. a_c no es constante sino que es función de la posición x. La ecuación del movimiento no se puede integrar fácilmente.

Curva de la energía potencial

El centro de masas del cilindro se mueve como una partícula cuya masa es igual a la masa m del cilindro, bajo la acción de la fuerza F=ma_c.

La fuerza F es una función de la posición x del c.m. del cilindro. Se trata por tanto, de una fuerza conservativa. El trabajo de la fuerza conservativa F, es igual a la diferencia entre la energía potencial inicial y la final.

${\displaystyle {\displaystyle \underset{0}{\overset{x}{\int }}Fdx}=E_p(0)-E_p(x)}$

Tomando E_p(0)=0.

${\displaystyle E_p(x)=-\frac{2}{3}mg\sin \theta ·x+\frac{2}{3}\mu B\sin \left(\frac{x}{R}\right)}$

Escribimos la energía potencial en términos de las variables adimensionales z=x/R, y A=μB/(mgRsinθ), y V(z)=E_p(x)/(2mgR/3), quedando

V(z)=-z+Asin(z)

Calculamos los extremos de esta función

${\displaystyle \begin{array}{l}\frac{dV}{dz}=-1+A\cos (z)=0\\ \frac{d^{2}V}{d{z}^2}=-A\sin (z)\end{array}}$

Son máximos cuando la derivada segunda es negativa y son mínimos cuando la derivada segunda es positiva. Llamando φ=arcos(1/A), con A≥1.

• Los máximos se producen para z_n=φ+2nπ
• Los mínimos para z_n= -φ+2nπ

En los extremos (máximos y mínimos) la fuerza neta que actúa sobre el c.m. del cilindro es cero. Estas son las posiciones de equilibrio: estable en los mínimos e inestable en los máximos.

A=4; %parámetro
f=@(x) A*sin(x)-x;
hold on
fplot(f, [-10,10])
z=acos(1/A);
for n=-1:1
%máximos
    plot(z+n*2*pi,f(z+n*2*pi),'o','markersize',3,'markeredgecolor',
'r','markerfacecolor','r')
%mínimos
    plot(-z+n*2*pi,f(-z+n*2*pi),'o','markersize',3,'markeredgecolor',
'b','markerfacecolor','b')
end
hold off
set(gca,'XTick',-2*pi:pi:2*pi)
set(gca,'XTickLabel',{'-2\pi','-\pi','0','\pi','2\pi'})
grid on
xlabel('z')
ylabel('V(z)')
title('Energía potencial')

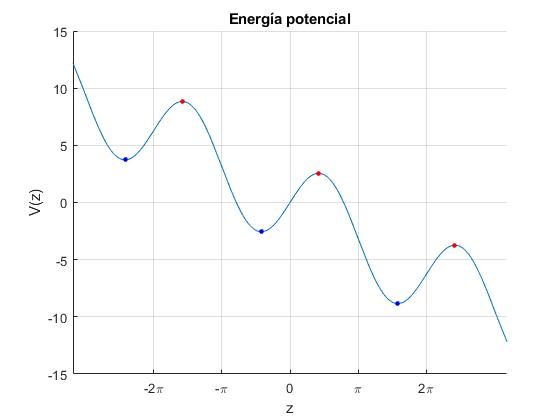
La representación gráfica de V(z) en función de la variable adimensional z, nos permite describir cualitativamente el movimiento del c.m. del cilindro para una energía total ε dada.

El código para representar una parte de la figura es

function atwood_1
    A=4; %parámetro
    E=7; %energía 
    f=@(x) A*sin(x)-x;
    fm=@(x) f(x)-E;
    x=linspace(-10,10,20);
    r=raices(fm,x);
    hold on
    fplot(f, [-10,10])
    line([-10,10],[E,E],'color','k');
%dibuja las raíces
    ordenada=ones(1,length(r))*E;
    plot(r, ordenada,'ro','markersize',4,'markerfacecolor','r')
    hold off
    %grid on
    xlabel('z')
    ylabel('V(z)')
    title('Energía potencial')
    
    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)>0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

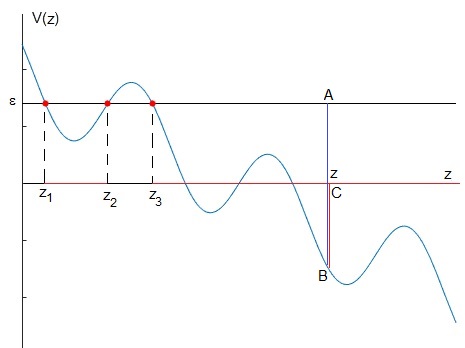
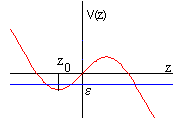
Como se aprecia en la figura, para la energía total ε hay dos regiones en las que se pueden mover el cilindro, aquellas en las que su energía cinética es positiva o bien aquellas en las que la energía total ε es mayor que la energía potencial V(z). La condición ε≥V(z), se cumple para los puntos z en el segmento z₁≤z≤z₂ y en la semirrecta z≥z₃ . Siendo z₁, z₂ y z₃ las raíces de la ecuación trascendente ε=V(z).

La posición inicial del c.m. del cilindro determina la región en la que se moverá posteriormente. Imaginemos que el cilindro se encuentra en la posición z≥z₃, señalada en la figura. Su energía potencial es el segmento CB, la energía total es el segmento CA, luego la energía cinética (de traslación y de rotación) es el segmento AB. El punto de intersección z₃ entre la recta y la función energía potencial, V(z)=ε, marca el punto de retorno, es decir, aquél en el que la velocidad del c.m. del cilindro es nula.

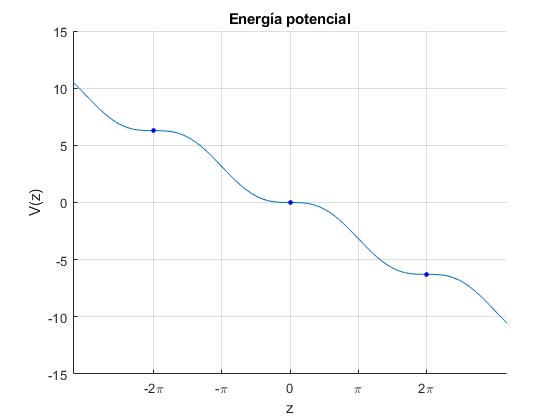
Cuando A=1, no hay máximos ni mínimos locales, los puntos z=0, ±2π, ±4π, son de inflexión ya que la primera y segunda derivadas son nulas en dichos puntos. dV/dz=0, y d²V/dz²=0.

Ecuación del movimiento del cilindro

La aceleración del c.m. a_c de cilindro no es constante, sino que depende de la posición x del cilindro. Escribimos la ecuación diferencial del movimiento en función del parámetro adimensional z=x/R.

${\displaystyle \frac{d^{2}z}{d{t}^2}=C(1-A\cos z)C=\frac{2g\sin \theta }{3R}A=\frac{\mu B}{mRg\sin \theta }}$

Se resuelve la ecuación diferencial mediante el procedimiento numéricos con las condiciones iniciales z=z₀ y dz/dt=0 en el instante t=0, siendo z₀ un punto de retorno o una de las raíces de la ecuación transcendente ε=V(z).

El comportamiento del sistema viene determinado por el parámetro A, ya que el parámetro C actúa de factor de escala. Fijado el valor de C, lo que equivale a fijar el ángulo θ del plano inclinado para un valor dado del radio R del cilindro, se puede cambiar el parámetro A modificando el valor del campo magnético B, es decir, modificando la intensidad de la corriente que produce dicho campo.

1. Cuando A>1 el cilindro se comporta de dos maneras distintas

• El cilindro oscila entre dos posiciones.

• El cilindro baja rodando sin deslizar a lo largo del plano inclinado.

E=2.2; %energía
A=4; %parámetro
fm=@(x) -x+A*sin(x);
f=@(x) fm(x)-E;
x=linspace(-10,10,50);
r=raices(f,x);

x0=[r(1),0]; %posición inicial, cambiar a otro índice 2 ó 3
f=@(t,x) [x(2); 1-A*cos(x(1))]; 
[t,x]=ode45(f,[0 10],x0);
plot(t,x(:,1))
grid on
xlabel('t')
ylabel('x');
title('Movimiento de la rueda')



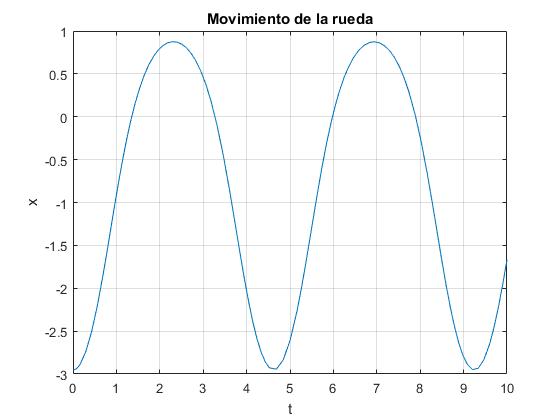
Observamos el movimiento periódico, medimos en la gráfica, utilizando, Data cursor, el periodo de oscilación, la distancia entre dos máximos o entre dos mínimos. Si cambiamos la posición inicial x0(1)=raices(3);, el movimiento deja de ser períódico. La rueda se mueve a lo largo del plano inclinado y no regresa



2. Para A≤1 el cilindro siempre baja rodando a lo largo del plano inclinado.

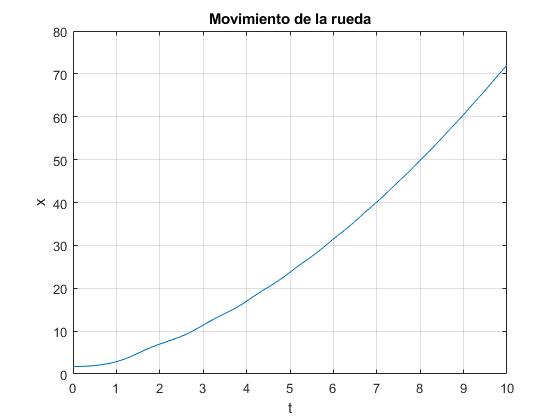
Oscilaciones de pequeña amplitud alrededor de una posición de equilibrio

Si desarrollamos en serie la función f(z)=C(1-Acos(z)), alrededor de la posición de equilibrio (mínimo de la energía potencial) z₀=-arccos(1/A).

${\displaystyle \begin{array}{l}f(z)=f(z_0)+{\left(\frac{df}{dz}\right)}_{z_0}(z-z_0)+\mathrm{...}\\ f(z)\approx CA\sin (z_0)(z-z_0)=-C\sqrt{A^2-1}(z-z_0)\end{array}}$

La ecuación del movimiento se transforma en la ecuación diferencial de un M.A.S.

${\displaystyle \frac{d^2\zeta }{d{t}^2}+{\omega }^2\zeta =0\zeta =z-z_0}$

La frecuencia angular ω del M.A.S. es

${\displaystyle \omega =\sqrt{C\sqrt{A^2-1}}}$

Actividades

Se introduce

1. El valor del parámetro A, en el control titulado Parámetro
2. El valor de la energía total ε, en el control titulado Energía

Se pulsa el botón titulado Nuevo

El programa interactivo calcula las raíces de la ecuación transcendente ε=V(z), situando al cilindro aleatoriamente es en una de las posiciones de retorno con velocidad inicial nula. A continuación, resuelve la ecuación diferencial del movimiento por el procedimiento de Runge-Kutta, para calcular la posición del cilindro en función del tiempo.

El parámetro C se ha fijado en el valor C=1, el radio del cilindro se ha fijado en R=1, lo que equivale a fijar el ángulo del plano inclinado en el valor θ=8.8º.

Cuando se introduce el valor de A, se representa gráficamente de V(z) en función de z, la energía total ε se representa mediante una línea horizontal. Un segmento vertical de color azul en la posición del c.m. del cilindro indica su energía cinética (de traslación y de rotación).

En la parte inferior, se observa el movimiento del cilindro sobre el plano inclinado. Con origen en su c.m. se han dibujado.

• El campo magnético (una flecha de color azul que apunta hacia arriba).
• El momento magnético del imán (una flecha de color rojo, que gira con el cilindro).
• La fuerza F neta que actúa sobre el c.m. del cilindro, (una flecha de longitud variable de color negro).

Fijarse que la fuerza F es nula en los máximos y en los mínimos de V(z), es positiva cuando la pendiente de V(z) es negativa y es negativa cuando la pendiente es positiva.

Ejemplos

Para A=4 observamos una sucesión de máximos y mínimos locales en las posiciones siguientes:

• Máximos: -4.97, 1.32, 7.6…
• Mínimos: -7.60, -1.32, 4.97

Introducimos una energía ε=2.2. Las raíces de la ecuación transcendente ε=V(z) son

z₁=-2.95, z₂=0.88, z₃=1.74

El cilindro tiene dos posibles movimientos

• Oscila entre las posiciones z₁≤z≤z₂
• Baja rodando sin deslizar desde la posición z₃ en adelante

Al pulsar el botón titulado Nuevo, se selecciona aleatoriamente una de las tres posiciones de partida.

Cuando la energía total es ε=-1.5 próxima al mínimo local de V(z) el cilindro oscila con un periodo del 3.3 s entre las posiciones z₁=-2.05 y z₂=-0.53. Este periodo es un poco mayor que el que se obtiene mediante la fórmula aproximada.

${\displaystyle \omega =\sqrt{C\sqrt{A^2-1}}=\sqrt{\sqrt{\text{15}}}P=\frac{2\pi }{\omega }=3.2\text{s}}$

Los valores del tiempo t, la posición z y la velocidad v del c.m. del cilindro se muestra en la esquina superior izquierda.

Para A=1. Si introducimos una energía ε=0, el cilindro permanece en esta posición de equilibrio.

Para A=0.3. Si introducimos una energía ε=0, el cilindro baja rodando a lo largo del plano inclinado desde la posición inicial z₀=0. Este tipo de movimiento se produce para cualquier valor de la energía ε.

Referencias

Lucília Brito, Manuel Fiolhais, José Paixão. Cylinder on an incline as a fold catastrophe system. Eur. J. Phys. 24 (2003) pp. 115-123.