En muchos dispositivos que utilizan una corriente para crear un campo magnético, tales como un electroimán o un transformador, el hilo que transporta la corriente está arrollado en forma de bobina formada por muchas espiras. Estudiaremos, en primer lugar, el campo creado por una espira.

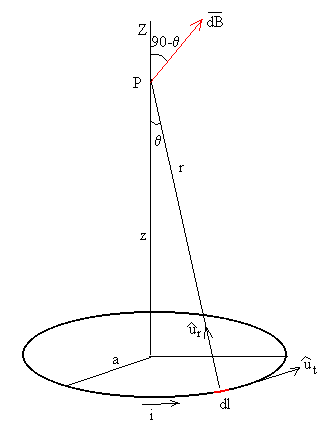
En la figura, se muestra una espira circular de radio a, recorrida por una corriente de intensidad i. El punto P está sobre el eje de la espira a una distancia z de su centro.

Sea r la distancia entre el elemento de corriente y el punto P. La ley de Biot nos permite calcular el campo magnético creado por dicho elemento de corriente.

${\displaystyle \begin{array}{l}\overrightarrow{dB}=\frac{{\mu }_{0}i}{4\pi }\frac{{\widehat{u}}_t\times {\widehat{u}}_r}{r^2}dl\\ dB=\frac{{\mu }_{0}i}{4\pi }\frac{dl}{r^2}\end{array}}$

Los vectores unitarios ${\widehat{u}}_t$ y ${\widehat{u}}_r$ forman 90º

El vector campo magnético $\overrightarrow{dB}$ tiene dos componentes

• a lo largo del eje de la espira dB·cos(90-θ)
• perpendicular al eje de la espira dB·sin(90-θ)

Por razón de simetría, las componentes perpendiculares al eje creadas por elementos diametralmente opuestos se anulan entre sí. Por tanto, el campo magnético resultante está dirigido a lo largo del eje y puede calcularse mediante una integración sencilla ya que r es constante y θ es constante

${\displaystyle B={\displaystyle \int dB·\cos (90-\theta )}=\frac{{\mu }_{0}i}{4\pi r^2}\sin \theta {\displaystyle \oint dl}=\frac{{\mu }_{0}i}{4\pi r^2}2\pi a\sin \theta ·=\frac{{\mu }_{0}i{a}^2}{2{\left(\sqrt{z^2+a^2}\right)}^3}}$

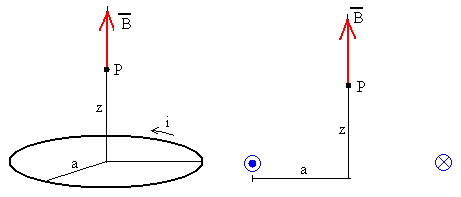
En el centro de la espira z=0, tenemos

${\displaystyle B=\frac{{\mu }_{0}i}{2a}}$

El sentido del campo magnético viene determinado por la regla de la mano derecha.

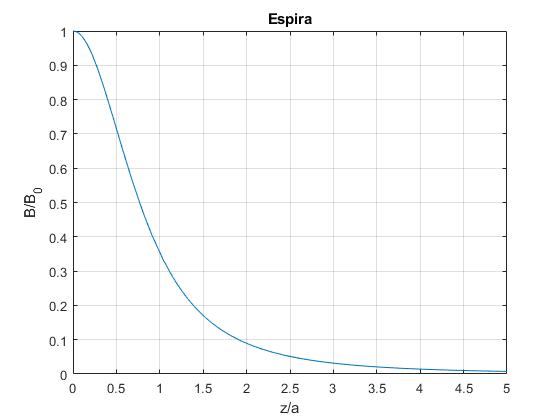
Representamos el campo magnético B/B₀ en función de z/a. B₀ es el campo magnético en el centro z=0 de la espira

f=@(x) 1./(1+x.^2).^(3/2);
fplot(f,[0,5])
grid on
xlabel('z/a')
ylabel('B/B_0')
title('Espira')

Disco cargado en rotación

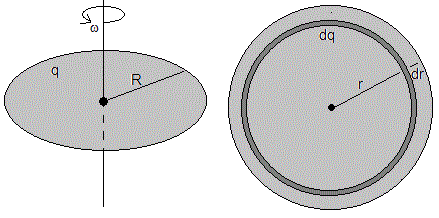
Un disco de plástico de radio R tiene una carga q uniformemente distribuida en su superficie. Si el disco gira con velocidad angular constante ω alrededor de un eje perpendicular al plano del disco y que pasa por su centro. Calcula el campo magnético producido en el centro del disco.

La carga dq que hay en el anillo de radio r y anchura dr, de color oscuro en la figura es

${\displaystyle dq=q\frac{2\pi r·dr}{\pi R^2}}$

Esta carga dq que gira con velocidad angular ω es equivalente a una espira de radio r por la que circula una corriente di

${\displaystyle di=fdq=\frac{\omega }{2\pi }\frac{2qr}{R^2}dr}$

El campo magnético producido por esta corriente en su centro es

${\displaystyle dB=\frac{{\mu }_{0}di}{2r}={\mu }_0\frac{\omega q}{2\pi R^2}dr}$

Los campos producidos por todas las cargas que giran tienen la misma dirección, perpendicular al plano del disco, y sentido

${\displaystyle B={\displaystyle \underset{0}{\overset{R}{\int }}{\mu }_0\frac{\omega q}{2\pi R^2}dr}={\mu }_0\frac{\omega q}{2\pi R}}$

Las bobinas de Helmholtz

Considremos el campo producido por dos bobinas iguales de radio a de N espiras apretadas recorridas por una corriente eléctrica de intensidad i y separadas una distancia d, tal como se aprecia en la figura.

Situamos el origen en el punto medio O entre las dos bobinas y calculamos el campo magnético en un punto z del eje común de las dos bobinas

${\displaystyle \begin{array}{l}B=B_1+B_2=\frac{{\mu }_{0}Ni{a}^2}{2{\left({\left(z+\frac{d}{2}\right)}^2+a^2\right)}^{3/2}}+\frac{{\mu }_{0}Ni{a}^2}{2{\left({\left(z-\frac{d}{2}\right)}^2+a^2\right)}^{3/2}}=\\ \frac{{\mu }_{0}Ni}{2a}\left(\frac{1}{{\left({\left(\frac{z}{a}+\frac{d}{2a}\right)}^2+1\right)}^{3/2}}+\frac{1}{{\left({\left(\frac{z}{a}-\frac{d}{2a}\right)}^2+1\right)}^{3/2}}\right)\end{array}}$

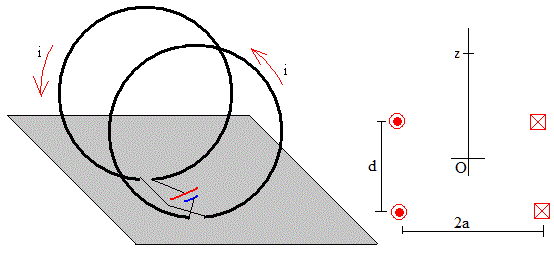
Representamos el campo magnético B en función de z/a en unidades de B₀=μ₀Ni/2a, para tres valores de d/a: 0.5, 1, 2. Como vemos cuando z=0, el campo magnético presenta un máximo si d<a, un mínimo, si d>a y es casi uniforme en el intervalo -a/2<z<a/2 si d=a. Este último, es el caso que nos interesa

${\displaystyle B=\frac{8{\mu }_{0}Ni}{5\sqrt{5}a}=\frac{32\pi Ni}{5\sqrt{5}a}·{10}^{-7}\text{T}}$

hold on
d=0.5;
B=@(z) 1/sqrt((z+d/2)^2+1)^3+1/sqrt((z-d/2)^2+1)^3;
fplot(B,[-1.5,1.5])
d=1;
B=@(z) 1/sqrt((z+d/2)^2+1)^3+1/sqrt((z-d/2)^2+1)^3;
fplot(B,[-1.5,1.5])
d=2;
B=@(z) 1/sqrt((z+d/2)^2+1)^3+1/sqrt((z-d/2)^2+1)^3;
fplot(B,[-1.5,1.5])
hold off
grid on
legend('d=0.5','d=1','d=2')
xlabel('z/a')
ylabel('B/B_0')

En la página titulada Campo magnético producido por una corriente circular en un punto fuera de su eje se encuentra un estudio más detallado del campo magnético de las bobinas de Helmholtz

Medidas tomadas en el laboratorio

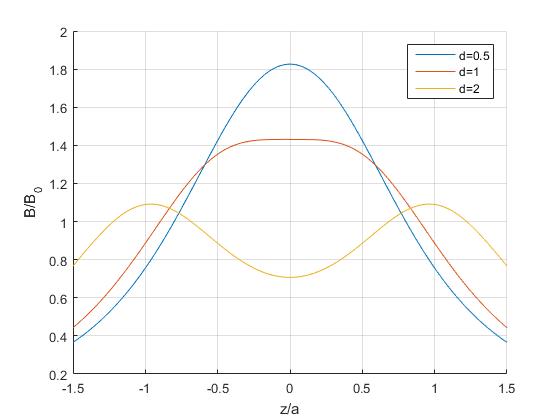
Disponemos de dos bobinas paralelas de radio a=10 cm y las separamos d=a para comprobar que el campo magnético es casi constante en el intervalo -a/2<z<a/2 y luego, disminuye rápidamente cuando nos alejamos del centro de las bobinas.

z se mide en cm desde el centro de las dos bobinas

x=[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19];
y=[7.7, 7.7, 7.7, 7.7, 7.7, 7.5, 7.3, 7.2, 6.7, 6.1, 
5.2, 4.7, 4.3, 3.9, 3.7, 3.3, 2.9, 2.5, 2.4, 2.2];
hold on
plot(x,y,'ro','markersize',3,'markerfacecolor','r')
plot(x,y)
hold off
grid on
xlabel('z(cm)')
ylabel('B(gauss)')
title('Bobinas de Helmholtz')

Medida del campo magnético terrestre

En este apartado utilizamos las bobinas de Helmholtz para medir la componente horizontal del campo magnético terrestre

Colocamos una brújula en el centro de las bobinas, las giramos hasta conseguir que la aguja esté orientada en la dirección perpendicular al eje de las bobinas. Cuando hacemos pasar una corriente, la aguja se desvía un ángulo θ tal como vemos en la fotografía

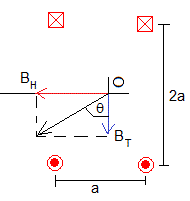
Cuando se conecta la corriente, las bobinas producen en su centro,un campo magnético B_H en la dirección del eje y sentido la regla de la mano derecha, cuyo módulo es

${\displaystyle B_H=\frac{8{\mu }_{0}Ni}{5\sqrt{5}a}=\frac{32\pi Ni}{5\sqrt{5}a}·{10}^{-7}T}$

Con N=500 espiras, de radio a=0.1 m, la intensidad de la corriente es i=0.11 A, producen un campo magnético B_H=4.94·10^-4 T

El ángulo medido ha sido θ=60°

${\displaystyle B_T=\frac{B_H}{\tan \theta }}$

por lo que B_T=2.85·10^-4 T. Aunque los resultados del experimento no sean buenos, es un ejemplo ilustrativo de la interacción entre corrientes e imanes

Referencias

Para el apartado, Medida del campo magnético terrestre

Jonathan E. Williams. Measuring Earth's Local Magnetic Field Using a Helmholtz Coil. The Physics Teacher, Vol. 52, April, 2014, pp. 236-238

M. Sosa, J. Bernal-Alvarado, J. L. González-Solis, G. Gutiérrez-Juárez, M. Vargas-Luna, M. Durán-Santamaría, S. P. Preciado-Galván, A. Ruiz-Velasco, V. D. Trujillo-García. A tangent magnetometer to measure the earth magnetic field. Revista Mexicana de Física. 49 (4) 379-383