Componentes del campo magnético producido por un solenoide
Campo magnético producido por una espira
En la página titulada Campo magnético producido por una corriente circular en un punto fuera de su eje calculamos las componenentes (radial y a lo largo del eje de la espira) del campo magnético prodicido por una espira cuyo centro estaba en el origen de coordenadas
Ahora calcularemos las componenentes de dicho campo para una espira cuyo centro está en el eje Z a una altura ζ
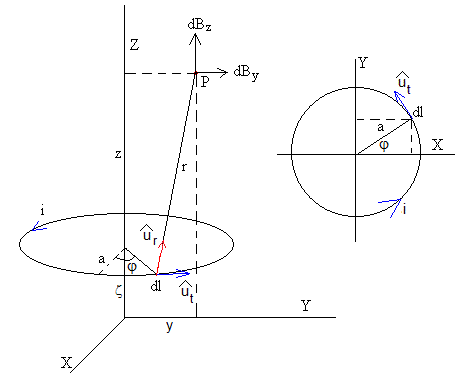
El campo producido por una espira de radio a tiene simetría axial, bastará calcular las componentes By y Bz del campo magnético en un punto P (0, y, z) del plano YZ.
Como vemos en la figura, la distancia r entre el elemento de corriente dl=a·dφ que está situado en el punto (a·cosφ, a·sinφ, ζ) y el punto P (0, y, z) considerado es
Efectuando el producto vectorial , obtenemos las componentes del campo
La primera integral es inmediata y vale cero, Bx=0, ya que para cada elemento de corriente dl existe otro simétrico al plano OYZ cuyo efecto es el de anular la componente X del campo magnético
Las componentes del campo son
Debido a la simetría cilíndrica del problema, solamente tenemos dos componentes del campo una a lo largo del eje de simetría Z, Bz y la otra By en la dirección radial, que a partir de ahora denominaremos Bρ (coordenadas cilíndricas) sustituyendo y por ρ.
Hacemos el cambio de variable, θ=π/2-φ
Componentes del campo magnético producido por un solenoide
Sea un solenoide de radio a, longitud 2b de n espiras por unidad de longitud, recorrido por una corriente de intensidad i
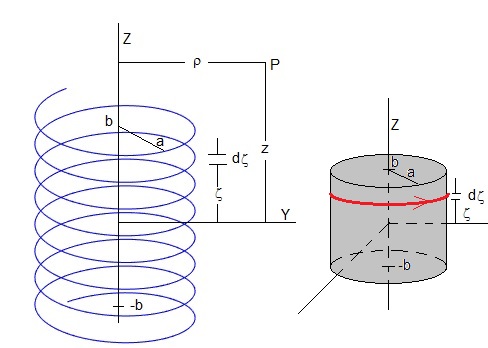
El código MATLAB para trazar la espiral es
t=0:0.05:16*pi; x=1.1*sin(t); y=1.1*cos(t); z=0.1*t; plot3(x,y,z,'b') view(-44,24) axis off
Por las espiras comprendidas entre ζ y ζ+dζ circula una corriente in·dζ que crea un campo magnético cuyas componentes son
Para hallar el campo total integramos respecto de ζ
Se hace el cambio u=(z-ζ)/c. La primera integral es inmediata,
Para la segunda integral, se hace después el cambio u=sinht
El resultado es
La integral elíptica completa
Transformamos las integrales en la forma de una integral elíptica completa para realizar su integración numérica. Esta función depende de cuatro parámetros k, c, p, c, s
El código MATLAB que realiza la integración numérica es
function res = integral_eliptica(kc,p,c,s)
if kc==0
res=NaN;
quit;
end
errtol=0.000001;
k=abs(kc);
pp=p;
cc=c;
ss=s;
em=1;
if p>0
pp=sqrt(p);
ss=s/pp;
else
f=kc^2;
q=1-f;
g=1-pp;
f=f-pp;
q=q*(ss-c*pp);
pp=sqrt(f/g);
cc=(c-ss)/g;
ss=-q/(g^2*pp)+cc*pp;
end
f=cc;
cc=cc+ss/pp;
g=k/pp;
ss=2*(ss+f*g);
pp=g+pp;
g=em;
em=k+em;
kk=k;
while abs(g-k)>g*errtol
k=2*sqrt(kk);
kk=k*em;
f=cc;
cc=cc+ss/pp;
g=kk/pp;
ss=2*(ss+f*g);
pp=g+pp;
g=em;
em=k+em;
end
res=(pi/2)*(ss+cc*em)/(em*(em+pp));
end
Para transformar las integrales en la forma conveniente, para su cálculo numérico mediante la función
cosθ=-cos(pi-θ)=-cos(2ψ)=sin2ψ-cos2ψ
De forma similar para la expresión de la derecha bajo la raíz. La componente del campo Bρ es
Para calcular la componente Bz hay que hacer además las transformaciones
La componente Bz es
Los seis parámetros valen
Definimos la función
function [By,Bz] = calcula_campo(a,b,y,z)
z_M=z+b;
z_m=z-b;
alfa_M=a/sqrt(z_M^2+(y+a)^2);
alfa_m=a/sqrt(z_m^2+(y+a)^2);
beta_M=z_M/sqrt(z_M^2+(y+a)^2);
beta_m=z_m/sqrt(z_m^2+(y+a)^2);
gamma=(a-y)/(a+y);
k_M=sqrt((z_M^2+(a-y)^2)/(z_M^2+(a+y)^2));
k_m=sqrt((z_m^2+(a-y)^2)/(z_m^2+(a+y)^2));
By=alfa_M*integral_eliptica(k_M,1,1,-1)-alfa_m*integral_eliptica(k_m,1,1,-1);
Bz=(a/(a+y))*(beta_M*integral_eliptica(k_M,gamma^2,1,gamma)-
beta_m*integral_eliptica(k_m,gamma^2,1,gamma));
end
Líneas de campo
Utilizamos esta función para trazar las líneas de campo de un solenoide de radio a=4 y longitud 2b=16
b=8; %longitud 2b
a=4; %radio
paso=0.1;
hold on
N=250;
for k=1:0.5:5
y=zeros(1,N+1);
z=zeros(1,N+1);
y(1)=-a+(2*a)*k/6;
z(1)=0;
for i=1:N
[By,Bz]=calcula_campo(a,b,y(i),z(i));
y(i+1)=y(i)+By*paso/(By^2+Bz^2);
z(i+1)=z(i)+Bz*paso/(By^2+Bz^2);
end
plot(y,z,'r')
plot(y,-z, 'r')
end
line([a,a],[-b,b],'lineWidth',1.5,'color','k')
line([-a,-a],[-b,b],'lineWidth',1.5,'color','k')
line([-a,a],[b,b],'lineWidth',1.5,'color','k')
line([-a,a],[-b,-b],'lineWidth',1.5,'color','k')
hold off
axis equal
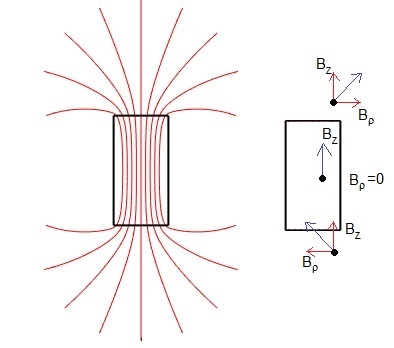
Componente radial, Bρ
El vector campo magnético , es tangente a las líneas de campo. Situando el origen de coordenadas en el centro del imán, vemos que la componente radial Bρ cambia de signo y es nula en el centro del solenoide
Sea un solenoide de radio a=1, de longitud 2b=2, representamos la componente radial Bρ en función de z del campo magnético producido por el solenoide en la posición ρ=0.9
a=1; %radio
b=1; %longitud 2b
zz=linspace(-5*b,5*b,200);
By=zeros(1, length(zz));
i=1;
y=0.9; %posición
for z=zz
[B_y,B_z]=calcula_campo(a,b,y,z);
By(i)=B_y;
i=i+1;
end
hold on
plot(zz,By)
line([b,b],[-0.5,0.5],'lineStyle','--','color','k') %extremo
line([-b,-b],[-0.5,0.5],'lineStyle','--','color','k')
grid on
xlabel('z')
ylabel('B_\rho')
title('Componente B_\rho')
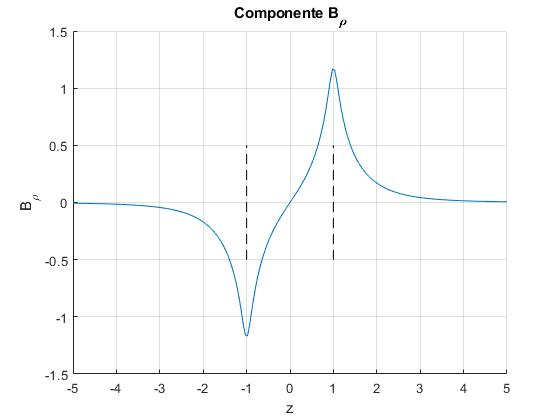
Las líneas a trazos marcan los extremos del solenoide en z=b y z=-b
Se suigiere al lector probar con solenoides más largos, por ejemplo b=3a, uno que triplique el diámetro
Componente a lo largo del eje, Bz
Sea un solenoide de radio a=1, de longitud 2b=6, representamos la componente a lo largo del eje Z, Bz en función de z del campo magnético producido por el solenoide en la posición ρ=0, eje del solenoide
a=1; %radio
b=3; %longitud 2b
zz=linspace(-3*b,3*b,200);
Bz=zeros(1, length(zz));
i=1;
y=0; %posición
for z=zz
[B_y,B_z]=calcula_campo(a,b,y,z);
Bz(i)=B_z;
i=i+1;
end
hold on
plot(zz,Bz)
line([b,b],[0,1],'lineStyle','--','color','k') %extremo
line([-b,-b],[0,1],'lineStyle','--','color','k')
grid on
xlabel('z')
ylabel('B_z')
title('Componente B_z')
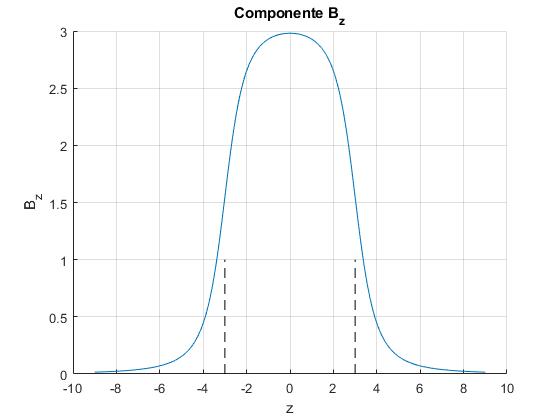
Las líneas a trazos marcan los extremos del solenoide en z=b y z=-b
Componentes del campo producido por una espira
En la página titulada Campo magnético producido por una corriente circular en un punto fuera de su eje calculamos las componentes del campo Bρ y Bz en el punto (ρ,z) utilizando integrales elípticas completas. En este apartado, vamos a volver a deducir las componentes del campo en términos de la función C(k, c, p, c, s), integral elíptica completa generalizada
Consideramos la espira como un solenoide de longitud 2b→0, que es recorrido por una corriente I=ni2b. n es el número de espiras por unidad de longitud
Las expresiones entre corchetes de las componentes del campo Bρ y Bz se desarrollan en serie tomando solamente el término proporcional a b, para ello nos ayudaremos de la función
Desarrollamos en serie, el término entre corchetes de Bρ
Para simplificar notaciones, llamamos s a sinψ, c a cosψ, d a (a+ρ) y e a (a-ρ)
syms z b c d e s; zz=taylor(1/(sqrt((z+b)^2+d^2)*sqrt(c^2+((z+b)^2+e^2)*s^2/((z+b)^2+d^2)))- 1/(sqrt((z-b)^2+d^2)*sqrt(c^2+((z-b)^2+e^2)*s^2/((z-b)^2+d^2))), b, 'order',2) zz=simplify(zz); latex(zz)
ans ='-\frac{2\,b\,z\,\left(c^2+s^2\right)}{{\left(d^2+z^2\right)}^{3/2}\,
{\left(\frac{c^2\,d^2+c^2\,z^2+e^2\,s^2+s^2\,z^2}{d^2+z^2}\right)}^{3/2}}'
Copiamos la salida
Transformamos la integral para que tome la forma de la función C(k, c, p, c, s), integral elíptica generalizada. La componente Bρ del campo creado por una espira de radio a recorrida por una intensidad I es
Desarrollamos en serie, el término entre corchetes de Bz
... zz=taylor((z+b)/(sqrt((z+b)^2+d^2)*sqrt(c^2+((z+b)^2+e^2)*s^2/((z+b)^2+d^2)))- (z-b)/(sqrt((z-b)^2+d^2)*sqrt(c^2+((z-b)^2+e^2)*s^2/((z-b)^2+d^2))), b, 'order',2) zz=simplify(zz); latex(zz)
ans ='\frac{2\,b\,\left(c^2\,d^2+e^2\,s^2\right)}{{\left(d^2+z^2\right)}^{3/2}\,
{\left(\frac{c^2\,d^2+c^2\,z^2+e^2\,s^2+s^2\,z^2}{d^2+z^2}\right)}^{3/2}}'
Copiamos la salida
Transformamos la integral para que tome la forma de la función C(k, c, p, c, s), integral elíptica generalizada. La componente Bz del campo creado por una espira de radio a recorrida por una intensidad I es
Comparamos las expresiones de las componentes del campo producido por la espira de radio a en términos de las integrales elípticas completas
Comprobación
Consideremos una espira de radio a=1. Calculamos la componente Bz del campo magnético producido por la espira a lo largo de su eje, ρ=0 por los dos procedimientos. Se sugiere al lector probar con otros valores, ρ=2
a=1; %radio
y=0; %posición
zz=linspace(0,5,100);
z=zz;
m=4*y./((1+y)^2+z.^2);
[K,E]=ellipke(m);
Bz=a*sqrt(m).*(a*(m.*E)./(2-2*m)+y*K-y*((2-m).*E)./(2-2*m))/(4*(a*y)^(3/2));
hold on
plot(z,Bz)
B_z=zeros(1, length(zz));
i=1;
gamma=(a-y)/(a+y);
for z=zz
k=sqrt((z^2+(a-y)^2)/(z^2+(a+y)^2));
B_z(i)=a*(y+a)*integral_eliptica(k,k^2,1,gamma)/(z^2+(y+a)^2)^(3/2);
i=i+1;
end
plot(zz, B_z)
hold off
grid on
xlabel('z')
ylabel('B_z')
title('Campo magnético producido por una espira')
Ambas gráficas coinciden
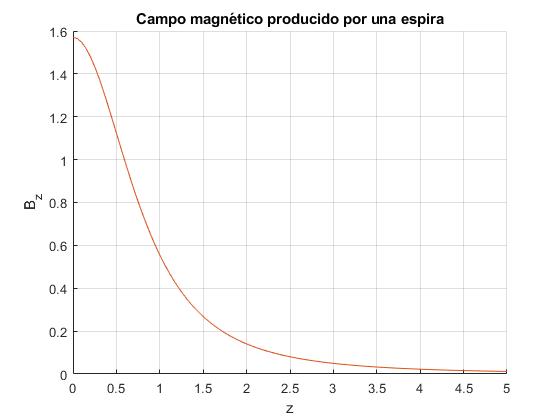
Calculamos la componente Bρ del campo magnético producido por la espira a una distancia z=2 del plano de la espira por los dos procedimientos
a=1; %radio
z=2; %distancia a la espira
yy=linspace(0,5,100);
y=yy;
m=4*y./((1+y).^2+z^2);
[K,E]=ellipke(m);
By=a*z*sqrt(m).*(-K+((2-m).*E)./(2-2*m))./(4*(a*y).^(3/2));
hold on
plot(y,By)
B_y=zeros(1, length(yy));
i=1;
for y=yy
gamma=(a-y)/(a+y);
k=sqrt((z^2+(a-y)^2)/(z^2+(a+y)^2));
B_y(i)=-a*z*integral_eliptica(k,k^2,1,-1)/(z^2+(y+a)^2)^(3/2);
i=i+1;
end
plot(yy, B_y)
hold off
grid on
xlabel('\rho')
ylabel('B_\rho')
title('Campo magnético producido por una espira')
Ambas gráficas coinciden
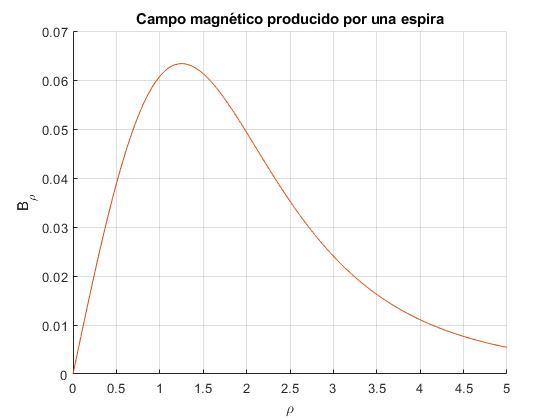
El procedimiento de cálculo de las componenentes Bρ y Bz del campo magnético producido por una espira, descrito en esta página, es más flexible ya que el código de la integral elíptica completa generalizada C(k, c, p, c, s) es corto y fácil de trasladar a cualquier lenguaje de programación
Referencias
Norman Derby, Stanislaw Olbert. Cylindrical magnets and ideal solenoids. Am. J. Phys. 78 (3) March 2010, pp. 229-235

