Fuerza entre dos espiras circulares paralelas

En la figura, se muestran dos espiras contenidas en planos paralelos de radio a y radio b separadas una distancia z. Las espiras conducen corrientes I_a e I_b, respectivamente.

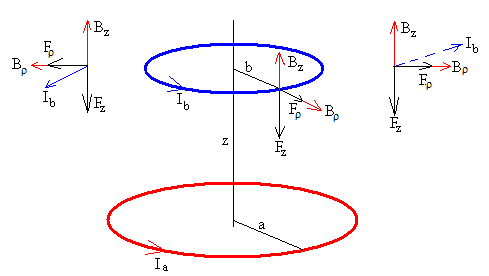
Si las corrientes tienen el mismo sentido, la fuerza es atractiva y si tienen sentido contrario, la fuerza es repulsiva.

El campo magnético producido por la espira de radio a, tiene dos componentes, uno radial B_ρ y la otra axial B_z.

La fuerza que ejerce el campo magnético producido por la espira inferior de radio a, sobre la corriente que circula por la espira superior de radio b es

${\displaystyle \overrightarrow{F}=I_b{{\displaystyle \oint }}^{\text{}}\left({\widehat{u}}_t\times \overrightarrow{B_a}\right)·d{l}_b}$

Como apreciamos en la figura, la componente B_z del campo magnético produce sobre un elemento de corriente una fuerza F_ρ cuya dirección es radial. La fuerza neta sobre la espira es cero.

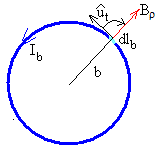
La componente radial B_ρ del campo produce sobre un elemento de corriente dl_b=b·dθ una fuerza cuya dirección es a lo largo del eje Z

• Positiva (repulsiva), si las corrientes tienen sentido contrario
• Negativa (atractiva) si las corrientes tienen el mismo sentido (como en la figura)

${\displaystyle F_z=-I_b{\displaystyle \oint (1·B_{\rho }·\sin 90º)·b·d\theta }=-2\pi B_{\rho }{I}_{b}b}$

Introduciendo el valor de la componente radial B_ρ del campo magnético producido por la espira de radio a para ρ=b.

${\displaystyle \begin{array}{l}{F}_z=-{\mu }_0{I}_a{I}_b\frac{z}{\sqrt{{(a+b)}^2+z^2}}\left(-K(m)+\frac{a^2+b^2+z^2}{{\left(a-b\right)}^2+z^2}E(m)\right)\hfill \\ m=\frac{4ab}{{(a+b)}^2+z^2}\hfill \end{array}}$

Cuando la segunda espira está alejada de la primera, aproximamos la primera a un dipolo magnético. La fuerza de atracción entre las espiras F_z se escribe

${\displaystyle F_z=-2\pi \left({\mu }_0{I}_a{a}^2\frac{3bz}{4{\left(\sqrt{z^2+b^2}\right)}^5}\right)I_{b}b=-{\mu }_0{I}_a{I}_b{a}^2{b}^2\frac{3\pi z}{2{\left(\sqrt{z^2+b^2}\right)}^5}}$

Supongamos que las espiras tienen el mismo radio a. Expresamos F_z en términos del cociente ζ=z/a

${\displaystyle \begin{array}{l}{F}_z=-{\mu }_0{I}_a{I}_b\frac{\varsigma }{\sqrt{4+{\varsigma }^2}}\left(-K(m)+\frac{2+{\varsigma }^2}{{\varsigma }^2}E(m) \right)\hfill \\ m=\frac{4}{4+{\varsigma }^2}\hfill \end{array}}$

En la aproximación de dipolo magnético, esta expresión se reduce a

${\displaystyle F_z=-{\mu }_0{I}_a{I}_b\frac{3\pi }{2}\frac{\varsigma }{{\left(\sqrt{{\varsigma }^2+1}\right)}^5}}$

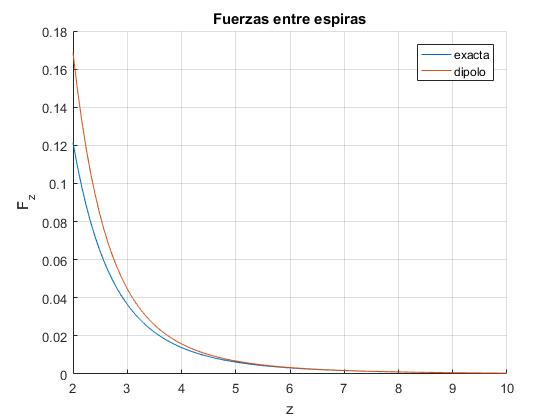
Representamos ambas expresiones de la fuerza entre dos espiras, la exacta y la aproximada, considerando la primera espira como un dipolo magnético

z=linspace(2,10,100);
m=4./(4+z.^2);
[K,E]=ellipke(m);
Fz=(-K+((2+z.^2).*E)./z.^2).*z./sqrt(z.^2+4);
hold on
plot(z,Fz)
plot(z,(3*pi/2)*z./sqrt(z.^2+1).^5)
hold off
grid on
legend('exacta','dipolo')
xlabel('z')
ylabel('F_z')
title('Fuerzas entre dos espiras')

Fuerza y momento que ejerce una corriente rectilínea sobre una corriente helicoidal

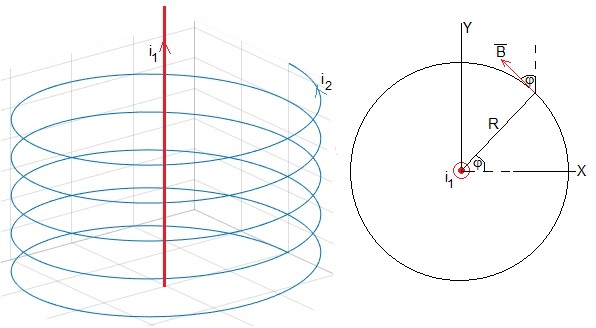
Consideremos una corriente rectilínea de intensidad i₁ que coincide con el eje Z de una corriente helicoidal de intensidad i₂. Las ecuaciones paramétricas de la hélice son

${\displaystyle \{\begin{array}{l}x=R\cos \phi \\ y=R\sin \phi \\ z=\frac{b}{2\pi }\phi \end{array}}$

Para representar parte de la figura, se ha empleado el código

R=1;
b=0.25;
fplot3(@(t) R*cos(t), @(t) R*sin(t), @(t) b*t/(2*pi),[0, 5*2*pi])
xlabel('x')
ylabel('y')
zlabel('z')
title('Hélice')

La corriente rectilínea produce un campo magnético en un punto P distante R, que en forma vectorial es

${\displaystyle \begin{array}{l}{B}_1=\frac{{\mu }_0{i}_1}{2\pi R}\\ {\overrightarrow{B}}_1=\frac{{\mu }_0{i}_1}{2\pi R}\left(-\sin \phi \widehat{i}+\cos \phi \widehat{j}\right)\end{array}}$

La fuerza que ejerce el campo magnético producido por el hilo rectilíneo sobre una porción de corriente helicoidal es

${\displaystyle \overrightarrow{dF}=i_2\left({\widehat{u}}_t\times \overrightarrow{B_1}\right)dl=i_2\left(\overrightarrow{dl}\times \overrightarrow{B_1}\right)}$

Un elemento diferencial de corriente helicoidal es

${\displaystyle \overrightarrow{dl}=dx\widehat{i}+dy\widehat{j}+dz\widehat{k}=\left(-R\sin \phi \widehat{i}+R\cos \phi \widehat{j}+\frac{b}{2\pi }\widehat{k}\right)d\phi }$

Efectuamos el producto vectorial

${\displaystyle \overrightarrow{dF}=\frac{{\mu }_0{i}_1{i}_2}{2\pi R}\left|\begin{array}{ccc}\widehat{i}& \widehat{j}& \widehat{k}\\ -R\sin \phi & R\cos \phi & \frac{b}{2\pi }\\ -\sin \phi & \cos \phi & 0\end{array}\right|d\phi =-\frac{{\mu }_0{i}_1{i}_2}{2\pi R}\frac{b}{2\pi }\left(\cos \phi \widehat{i}+\sin \phi \widehat{j}\right)d\phi }$

La fuerza sobre n vueltas desde el punto A, φ=0 hasta el B, φ=2nπ

${\displaystyle \overrightarrow{F}=-\frac{{\mu }_0{i}_1{i}_2}{2\pi R}\frac{b}{2\pi }\left\{\left({\displaystyle \underset{0}{\overset{2n\pi }{\int }}\cos \phi d\phi }\right)\widehat{i}+\left({\displaystyle \underset{0}{\overset{2n\pi }{\int }}\sin \phi d\phi }\right)\widehat{j}\right\}=0}$

Momento que ejerce el campo magnético

Calculamos el momento de las fuerzas $\overrightarrow{dF}$, respecto del origen

${\displaystyle \begin{array}{l}\overrightarrow{dM}=\overrightarrow{r}\times \overrightarrow{dF}\\ \overrightarrow{r}=R\cos \phi \widehat{i}+R\sin \phi \widehat{j}+\frac{b}{2\pi }\phi \widehat{k}\end{array}}$

Efectuamos el producto vectorial

${\displaystyle \begin{array}{l}\overrightarrow{dM}=-\frac{{\mu }_0{i}_1{i}_2}{2\pi R}\frac{b}{2\pi }\left|\begin{array}{ccc}\widehat{i}& \widehat{j}& \widehat{k}\\ R\cos \phi & R\sin \phi & \frac{b}{2\pi }\phi \\ \cos \phi & \sin \phi & 0\end{array}\right|d\phi \\ =\frac{{\mu }_0{i}_1{i}_2}{2\pi R}{\left(\frac{b}{2\pi }\right)}^2\left(\sin \phi \widehat{i}-\cos \phi \widehat{j}\right)\phi ·d\phi \end{array}}$

El momento sobre n vueltas de la hélice

${\displaystyle \overrightarrow{M}=\frac{{\mu }_0{i}_1{i}_2}{2\pi R}{\left(\frac{b}{2\pi }\right)}^2\left\{\left({\displaystyle \underset{0}{\overset{2n\pi }{\int }}\phi ·\sin \phi ·d\phi }\right)\widehat{i}-\left({\displaystyle \underset{0}{\overset{2n\pi }{\int }}\phi ·\cos \phi ·d\phi }\right)\widehat{j}\right\}}$

Integramos por partes

${\displaystyle \{\begin{array}{l}{\displaystyle \int \phi \sin \phi ·d\phi }=-\phi \cos \phi +\sin \phi \\ {\displaystyle \int \phi \cos \phi ·d\phi }=\phi \sin \phi +\cos \phi \end{array}}$

El resultado es

${\displaystyle \begin{array}{l}\overrightarrow{M}=\frac{{\mu }_0{i}_1{i}_2}{2\pi R}{\left(\frac{b}{2\pi }\right)}^2\left\{{\left(-\phi \cos \phi +\sin \phi \right)\widehat{i}-\left(\phi \sin \phi +\cos \phi \right)\widehat{j}|}_0^{2n\pi }\right\}\\ \overrightarrow{M}=-\frac{{\mu }_0{i}_1{i}_2}{2\pi R}{\left(\frac{b}{2\pi }\right)}^{2}2n\pi \widehat{i}=-\frac{{\mu }_0{i}_1{i}_2}{4{\pi }^{2}R}{b}^{2}n\widehat{i}\end{array}}$

Referencias

Félix Salazar Bloise, Rafael Medina Ferro, Ana Bayón Rojo, Francisco Gascón Latasa. Solved Problems in Electromagnetics. Springer (2017). Problem 5.29, pp. 304-306