Consideremos una placa conductora de anchura w y longitud muy grande. Calculamos el campo magnético en el punto P, producido por la corriente de intensidad i uniformente distribuida a lo largo de la anchura de la placa.

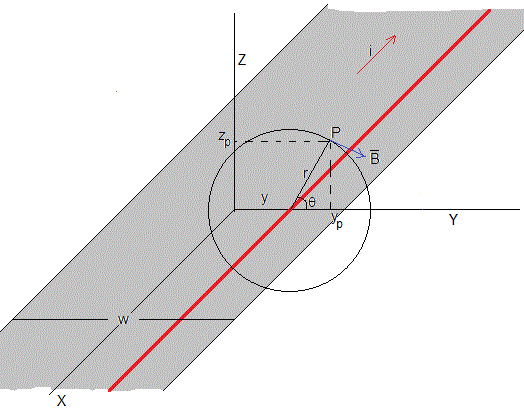
Dividimos la placa en corrientes rectilíneas, tal como se muestra en la figura, la intensidad de corriente que circula por cada hilo de anchura dy es i·dy/w, el campo magnético producido por dicha corriente en el punto P es

${\displaystyle dB={\mu }_0\frac{\frac{i}{w}dy}{2\pi r},r=\sqrt{{\left(y_p-y\right)}^2+z_p^2}}$

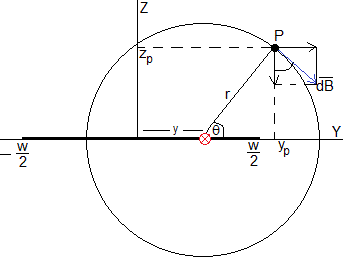
Su dirección es tangente a la circunferencia de radio r y sentido la regla de la mano derecha. Las componentes de dicho campo son

${\displaystyle \begin{array}{l}d{B}_y=\frac{{\mu }_{0}i}{2\pi w}\frac{dy}{r}\sin \theta =\frac{{\mu }_{0}i}{2\pi w}\frac{z_p}{{\left(y_p-y\right)}^2+z_p^2}dy\\ d{B}_z=-\frac{{\mu }_{0}i}{2\pi w}\frac{dy}{r}\cos \theta =\frac{{\mu }_{0}i}{2\pi w}\frac{y_p-y}{{\left(y_p-y\right)}^2+z_p^2}dy\end{array}}$

• La componente B_y producida por todas las corrientes rectilíneas que forman la placa es

${\displaystyle B_y=\frac{{\mu }_{0}i}{2\pi w}{z}_p{\displaystyle \underset{-w/2}{\overset{w/2}{\int }}\frac{dy}{{\left(y_p-y\right)}^2+z_p^2}}}$

Haciendo el cambio de variable

${\displaystyle \begin{array}{l}u=y_p-y,du=-dy\\ {\displaystyle \int \frac{du}{u^2+z_p^2}=}\frac{1}{z_p}\arctan \left(\frac{u}{z_p}\right)\\ B_y=-\frac{{\mu }_{0}i}{2\pi w}{z}_p\frac{1}{z_p}\left\{\arctan \left(\frac{y_p-\frac{w}{2}}{z_p}\right)-\arctan \left(\frac{y_p+\frac{w}{2}}{z_p}\right)\right\}\\ B_y=\frac{{\mu }_{0}i}{2\pi w}\left\{\arctan \left(\frac{y_p+\frac{w}{2}}{z_p}\right)-\arctan \left(\frac{y_p-\frac{w}{2}}{z_p}\right)\right\}\end{array}}$

• La componente B_z producida por todas las corrientes rectilíneas que forman la placa es

${\displaystyle B_z=-\frac{{\mu }_{0}i}{2\pi w}{\displaystyle \underset{-w/2}{\overset{w/2}{\int }}\frac{y_p-y}{{\left(y_p-y\right)}^2+z_p^2}dy}}$

Haciendo el cambio de variable

${\displaystyle \begin{array}{l}u={\left(y_p-y\right)}^2+z_p^2,du=-2\left(y_p-y\right)dy\\ {\displaystyle \int \frac{du}{u}}=\ln u\\ B_z=\frac{{\mu }_{0}i}{4\pi w}\left\{\ln \left({\left(y_p-\frac{w}{2}\right)}^2+z_p^2\right)-\ln \left({\left(y_p+\frac{w}{2}\right)}^2+z_p^2\right)\right\}=\\ B_z=-\frac{{\mu }_{0}i}{4\pi w}\ln \left(\frac{{\left(y_p+\frac{w}{2}\right)}^2+z_p^2}{{\left(y_p-\frac{w}{2}\right)}^2+z_p^2}\right)\end{array}}$

Casos particulares

• Campo magnético en puntos del eje Z, y_p=0

${\displaystyle \begin{array}{l}{B}_y=\frac{{\mu }_{0}i}{2\pi w}\left\{\arctan \left(\frac{w}{2z_p}\right)-\arctan \left(-\frac{w}{2z_p}\right)\right\}=\frac{{\mu }_{0}i}{\pi w}\arctan \left(\frac{w}{2z_p}\right)\\ B_z=0\end{array}}$

• Campo magnético en los puntos del eje Y, para y_p>w/2

${\displaystyle \begin{array}{l}{B}_y=0\\ B_z=-\frac{{\mu }_{0}i}{4\pi w}\ln \left(\frac{{\left(y_p+\frac{w}{2}\right)}^2}{{\left(y_p-\frac{w}{2}\right)}^2}\right)=-\frac{{\mu }_{0}i}{2\pi w}\ln \frac{y_p+\frac{w}{2}}{y_p-\frac{w}{2}}\end{array}}$

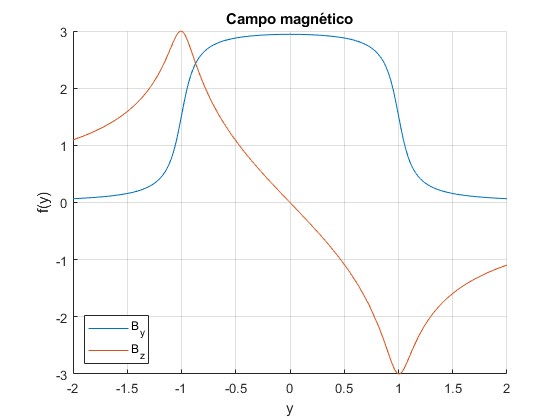
Representamos B_y y B_z en función de y_p para z_p=0.1, tomamos w/2=1 y la constante de proporcionalidad μ₀i/(2πw)=1

${\displaystyle \begin{array}{l}{B}_y=\arctan \left(\frac{y_p+1}{z_p}\right)-\arctan \left(\frac{y_p-1}{z_p}\right)\\ B_z=-\frac{1}{2}\ln \left(\frac{{\left(y_p+1\right)}^2+z_p^2}{{\left(y_p-1\right)}^2+z_p^2}\right)\end{array}}$

z=0.1;
B_y=@(y) atan((y+1)/z)-atan((y-1)/z);
B_z=@(y) -log(((y+1).^2+z^2)./((y-1).^2+z^2))/2;
hold on
fplot(B_y,[-2,2])
fplot(B_z,[-2,2])
hold off
grid on
legend('B_y','B_z','Location','best')
xlabel('y')
ylabel('f(y)')
title('Campo magnético')

Campo magnético producido por corrientes rectilíneas paralelas

Campo magnético producido por una corriente rectilínea

z=0.5;
y=1;
% th=atan(z/y);
r2=y^2+z^2;
Bz=-y/r2;
By=z/r2;
hold on
quiver(y,z,By,Bz)
quiver(-y,z,By,-Bz)
fplot(@(t) sqrt(r2)*cos(t), @(t) sqrt(r2)*sin(t),[0,2*pi])
hold off
% grid on
axis equal
xlabel('y')
ylabel('z')
title('Campo magnético')

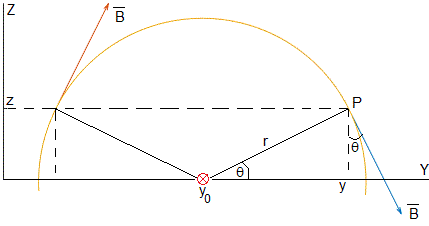
Una corriente rectilínea indefinida paralela al eje X, perpendicular al plano de la pantalla, está situada en (y₀,0), el campo magnético $\overrightarrow{B}$ en la posición P de coordenadas (y,z) es

${\displaystyle B=\frac{{\mu }_{0}i}{2\pi r},r^2={\left(y-y_0\right)}^2+z^2}$

cuya dirección es tangente a la circunferencia de radio r y sentido, la regla de la mano derecha. Sus componentes son

${\displaystyle \begin{array}{l}\overrightarrow{B}=\frac{{\mu }_{0}i}{2\pi r}\sin \theta \widehat{j}-\frac{{\mu }_{0}i}{2\pi r}\cos \theta \widehat{k}\\ \overrightarrow{B}=\frac{{\mu }_{0}i}{2\pi }\frac{z}{r^2}\widehat{j}-\frac{{\mu }_{0}i}{2\pi }\frac{y-y_0}{r^2}\widehat{k}\end{array}}$

Para representar el vector campo magnético en los puntos (y,z) tomaremos μ₀i/(2π)=1

Campo magnético producido por dos corrientes rectilíneas

Consideremos dos corrientes rectilíneas de la misma intensidad i, en el mismo sentido, situadas en y₀ y -y₀.

El campo magnético en el punto (y,z) es la suma de los campos producidos por cada una de las corrientes

z=0.5;
hold on
for y=-2:2:2
    Bz=0;
    By=0;
    for y0=[-1,1]
        r2=(y-y0)^2+z^2;
        Bz=Bz-(y-y0)/r2;
        By=By+z/r2;
    end
    quiver(y,z,By,Bz)
end
hold off
% grid on
axis equal
xlim([-2.5,2.5])
xlabel('y')
ylabel('z')
title('Campo magnético')

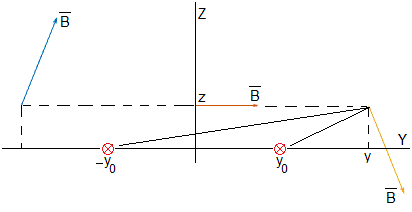
Por simetría, el campo magnético en el punto P de coordenadas (y=0, z) es horizontal, tal como se muestra la flecha roja de la figura.

Campo magnético producido por muchas corrientes rectilíneas

for z=-0.5:0.5
    for y=-6:2:6
        Bz=0;
        By=0;
        hold on
        for y0=-20:20
            r2=(y-y0)^2+z^2;
             Bz=Bz-(y-y0)/r2;
             By=By+z/r2;
         end
        quiver(y,z,By,Bz,0.25)
    end
end
hold off
% grid on
axis equal
xlabel('y')
xlim([-6.5,6.5])
ylabel('z')
title('Campo magnético')

Cuando hay muchas corrientes rectilíneas, situadas en k·y₀, k=0, ±1, ±2,...±20, el campo magnético es casi paralelo al eje Y, hacia la derecha para z>0 y hacia la izquierda para z<0

Cuando la placa es larga y ancha, el campo magnético $\overrightarrow{B}$ es constante y paralelo al eje Y en los puntos cercanos a la placa, hacia la derecha para z>0 y hacia la izquierda para z<0, tal como se muestra en la figura

Ley de Ampère

Aplicamos la ley de Ampére para determinar el módulo del campo magnético, eligiendo el camino rectangular cerrado ABCD de la figura.

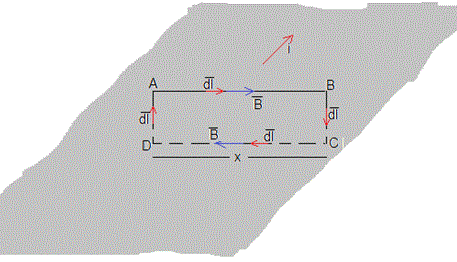
Si la intensidad i de la corriente está uniformemente distribuida en la anchura i de la placa, la que atraviesa el camino cerrado es ix/w.

${\displaystyle \begin{array}{l}{\displaystyle \oint \overrightarrow{B}·\overrightarrow{dl}}={\mu }_{0}i\\ {\displaystyle \underset{A}{\overset{B}{\int }}\overrightarrow{B}·\overrightarrow{dl}+}{\displaystyle \underset{B}{\overset{C}{\int }}\overrightarrow{B}·\overrightarrow{dl}}+{\displaystyle \underset{C}{\overset{D}{\int }}\overrightarrow{B}·\overrightarrow{dl}+}{\displaystyle \underset{D}{\overset{A}{\int }}\overrightarrow{B}·\overrightarrow{dl}}={\mu }_0\frac{i}{w}x\\ B·x+0+B·x+0={\mu }_0\frac{i}{w}x\\ B={\mu }_0\frac{i}{2w}\end{array}}$

Dos placas planas paralelas conductoras

El análogo a un condensador plano-paralelo son dos placas iguales anchas y largas, la corriente i que va por una de las placas regresa por la otra. Tenemos dos placas con corrientes uniformente distribuidas en sentidos contrarios.

for z=-1:1
    for y=-6:2:6
        Bz=0;
        By=0;
        hold on
        for z0=[-0.5,0.5]
            for y0=-20:20
                r2=(y-y0)^2+(z-z0)^2;
                Bz=Bz-sign(z0)*(y-y0)/r2;
                By=By+sign(z0)*(z-z0)/r2;
            end
        end
        quiver(y,z,By,Bz,0.25)
    end
end
hold off
axis equal
xlabel('y')
xlim([-6.5,6.5])
ylabel('z')
title('Campo magnético')

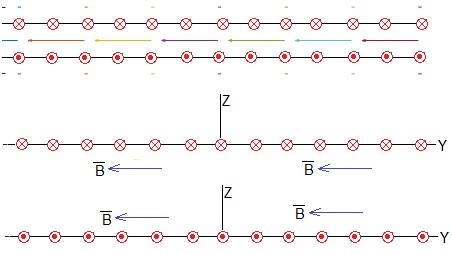
El campo magnético es casi nulo en el exterior y es el doble en el interior

${\displaystyle B_t=2B={\mu }_0\frac{i}{w}}$

Para minimizar los efectos de los bordes supondremos que la longitud l y la anchura w son grandes en comparación con las separación x entre las dos placas.

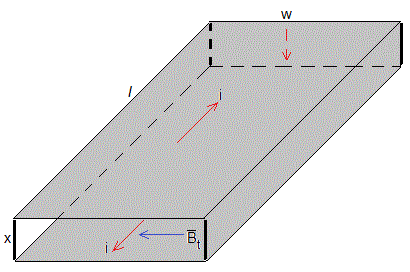
Fuerzas entre las placas

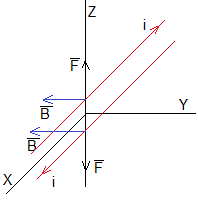
La fórmula de la fuerza que ejerce un campo magnético uniforme sobre una porción de corriente rectilínea es

${\displaystyle \overrightarrow{F}=i\left({\widehat{u}}_t\times \overrightarrow{B}\right)l}$

• El campo magnético producido por la placa superior es B=μ₀i/(2w), ejerce una fuerza sobre la corriente que circula por la placa inferior cuya longitud es l. Su módulo es

${\displaystyle \begin{array}{l}F=i\left({\mu }_0\frac{i}{2w}\right)l=\frac{1}{2}i{B}_{t}l\\ \overrightarrow{F}=-\frac{1}{2}i{B}_{t}l·\widehat{k}\end{array}}$

• El campo magnético producido por la placa inferior es B=μ₀i/(2w), ejerce una fuerza sobre la corriente que circula por la placa superior cuya longitud es l.

La fuerza es igual y de sentid contrario

${\displaystyle \overrightarrow{F}=\frac{1}{2}i{B}_{t}l·\widehat{k}}$

Las cargas de las placas de un condensador plano-paralelo son de signo contrario, las placas se atraen. En cambio las placas conductoras se repelen, por lo que es necesario ejercer una fuerza externa F_ext de la misma dirección y de signo contario para mantener la separación entre las placas

Trabajo y energía

Cuando se separan las placas muy despacio manteniéndolas paralelas se produce una fuerza electromotriz inducida de acuerdo con la ley de Faraday

${\displaystyle V_{\epsilon }=-\frac{d\Phi }{dt}}$

Si mantenemos una placa fija, la fem será proporcional a la velocidad de la placa móvil. Si la velocidad es muy pequeña, el flujo se mantendrá constante e igual al flujo inicial

${\displaystyle \begin{array}{l}\Phi =B_{t}lx=B_{0}l{x}_0\\ {\mu }_0\frac{i}{w}x=B_0{x}_0\end{array}}$

donde x₀ es la separación entre las placas en el instante inicial, cuando el campo magnético entre las placas es B₀

El módulo de la fuerza sobre la placa móvil vale

${\displaystyle F=\frac{1}{2}i{B}_{t}l=\frac{1}{2}\frac{B_0{x}_{0}w}{{\mu }_{0}x}\frac{B_0{x}_0}{x}l=\frac{wl}{2{\mu }_0}{B}_0^2\frac{x_0^2}{x^2}}$

El trabajo de la fuerza exterior es

${\displaystyle W=-{\displaystyle \underset{x_0}{\overset{x_f}{\int }}{F}_{ext}dx=-\frac{wl}{2{\mu }_0}{B}_0^2{x}_0^2}{\displaystyle \underset{x_0}{\overset{x_f}{\int }}\frac{dx}{x^2}}=\frac{wl}{2{\mu }_0}{B}_0^2{x}_0^2\left(\frac{1}{x_f}-\frac{1}{x_0}\right)}$

El signo negativo indica que la fuerza es de sentido contario al desplazamiento, si la separación aumenta x_f>x₀ el trabajo es negativo. En cambio, si la separación disminuye x_f<x₀ el trabajo es positivo, ya que la fuerza y el desplazamiento tienen el mismo sentido.

La energía magnética almacenada entre las dos placas es el producto de la densidad de energía magnética por el volumen del dispositivo

${\displaystyle U=\left(\frac{1}{2{\mu }_0}{B}_t^2\right)(wxl)=\frac{1}{2{\mu }_0}{\left(\frac{B_0{x}_0}{x}\right)}^2(wxl)=\frac{wl}{2{\mu }_0}\frac{B_0^2{x}_0^2}{x}}$

La variación de energía magnética es

${\displaystyle \Delta U=U_f-U_0=\frac{wl}{2{\mu }_0}\frac{B_0^2{x}_0^2}{x_f}-\frac{wl}{2{\mu }_0}\frac{B_0^2{x}_0^2}{x_0}=\frac{wl}{2{\mu }_0}{B}_0^2{x}_0^2\left(\frac{1}{x_f}-\frac{1}{x_0}\right)}$

Obtenemos el mismo resultado. El trabajo de la fuerza externa se invierte en modificar la energía magnética del sistema de dos placas conductoras paralelas

Coeficiente de autoinducción

La energía almacenada en un dispositivo magnético tiene la fórmula, alternativa

${\displaystyle \begin{array}{l}U=\frac{1}{2}L{i}^2=\frac{wl}{2{\mu }_0}\frac{B_0^2{x}_0^2}{x}\\ \frac{1}{2}L{\left(\frac{B_0{x}_{0}w}{{\mu }_{0}x}\right)}^2=\frac{wl}{2{\mu }_0}\frac{B_0^2{x}_0^2}{x}\\ L={\mu }_0\frac{lx}{w}\end{array}}$

Donde L es el coeficiente de autoinducción, que solamente depende de factores geométricos: anchura w, longitud l y separación x

Referencias

N. Gauthier. Relating the Stored Magnetic Energy of a Parallel-Plate Inductor to the Work of External Forces. The Physics Teacher. Vol. 45 November 2007, pp. 498-500