Campo magnético producido por un imán

Para calcular el campo magnético producido por un imán a lo largo de su eje, consideraremos la equivalencia existente entre corrientes e imanes. Sea un imán cilíndrico de radio a y longitud L. Si el momento magnético del imán es μ, la corriente equivalente I_eq que produce este momento magnético es

${\displaystyle I_{eq}=\frac{\mu }{\pi a^2}}$

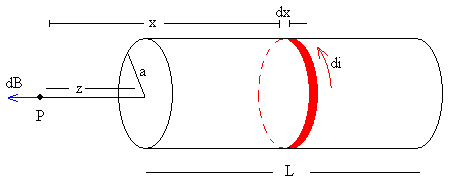
La corriente di que circula por la espira de anchura dx comprendida entre x y x+dx es

${\displaystyle di=\frac{I_{eq}}{L}dx=\frac{\mu }{\pi a^{2}L}dx}$

La corriente di que circula por esta espira de radio a produce en el punto P un campo magnético dB cuya dirección y sentido se señalan en la figura

${\displaystyle dB=\frac{{\mu }_0{a}^{2}di}{2{\left(\sqrt{a^2+x^2}\right)}^3}=\frac{{\mu }_0·\mu }{2\pi L{\left(\sqrt{a^2+x^2}\right)}^3}dx}$

Todas las espiras elementales producen en P un campo que tiene la misma dirección y sentido pero distinto módulo, dependiendo de su distancia x al punto P.

Para integrar, tenemos que hacer el cambio de variable a=x·tanθ y teniendo en cuenta que, 1+tan²θ =1/cos²θ , simplificamos la integral

${\displaystyle B=\frac{{\mu }_0\mu }{2\pi L{a}^2}{\displaystyle \underset{{\theta }_1}{\overset{{\theta }_2}{\int }}-\sin \theta ·d\theta }=\frac{{\mu }_0\mu }{2\pi L{a}^2}(\cos {\theta }_2-\cos {\theta }_1)}$

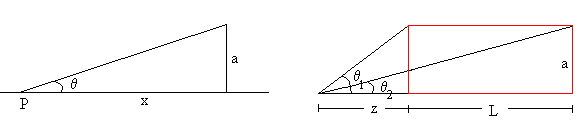
Donde

${\displaystyle \cos {\theta }_1=\frac{z}{\sqrt{z^2+a^2}}\cos {\theta }_2=\frac{z+L}{\sqrt{{(z+L)}^2+a^2}}}$

Conocidas las dimensiones del imán, su radio a y su longitud L, se puede medir el campo magnético B producido por el imán a una distancia z a lo largo de su eje y así, determinar mediante la fórmula anterior el momento magnético μ del imán.

Aproximaciones

La longitud L del imán es grande comparada con su radio a

${\displaystyle \begin{array}{l}B=\frac{{\mu }_0\mu }{2\pi L{a}^2}\left(\frac{z+L}{\sqrt{{\left(z+L\right)}^2+a^2}}-\frac{z}{\sqrt{z^2+a^2}}\right)=\\ =\frac{{\mu }_0\mu }{2\pi L{a}^2}\left(\frac{1}{\sqrt{1+{\left(\frac{a}{z+L}\right)}^2}}-\frac{1}{\sqrt{1+{\left(\frac{a}{z}\right)}^2}}\right)\approx \\ \frac{{\mu }_0\mu }{2\pi L{a}^2}\left(1-\frac{1}{2}{\left(\frac{a}{z+L}\right)}^2-1+\frac{1}{2}{\left(\frac{a}{z}\right)}^2\right)=\frac{{\mu }_0\mu }{4\pi L}\left(\frac{1}{z^2}-\frac{1}{{\left(z+L\right)}^2}\right)\end{array}}$

La longitud L del imán es pequeña comparada con la distancia z del imán al sensor

${\displaystyle B=\frac{{\mu }_0\mu }{4\pi }\frac{2+L/z}{z^3{\left(1+L/z\right)}^2}\approx \frac{{\mu }_0\mu }{2\pi }\frac{1}{z^3}}$

El campo magnético producido por el imán es inversamente proporcional al cubo de la distancia z entre el imán y el sensor

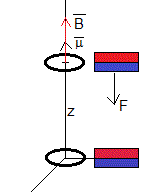
La energía de un dipolo magnético $\overrightarrow{\mu }$ en un campo magnético externo $\overrightarrow{B}$ es el producto escalar

${\displaystyle U=-\overrightarrow{\mu }·\overrightarrow{B}}$

Sean dos dipolos con el mismo momento magnético μ y sus ejes están alineados y separados una distancia z. El campo magnético producido por el primero en la posición del segundo es

${\displaystyle \overrightarrow{B}=\frac{{\mu }_0\mu }{2\pi }\frac{1}{z^3}\widehat{k}}$

La fuerza que ejerce el campo magnético producido por imán situado en el origen sobre el imán situado en la posición z es

${\displaystyle \begin{array}{l}U=-\left(\frac{{\mu }_0\mu }{2\pi }\frac{1}{z^3}\widehat{k}\right)\left(\mu \widehat{k}\right)=-\frac{{\mu }_0{\mu }^2}{2\pi }\frac{1}{z^3}\\ F=-\frac{dU}{dz}=-3\frac{{\mu }_0{\mu }^2}{2\pi }\frac{1}{z^4}\end{array}}$

En este caso la fuerza es atractiva, inversamente proporcional a la cuarta potencia de la distancia z.

Medidas efectuadas en el laboratorio

El campo producido por una carga puntual en un punto P distante z de la carga es inversamente proporcional al cuadrado de la distancia z, E=k/z².

x=[5,6,7,8,9,10,11];
y=[27,15,9.7,6.2,4.4,3.3,2.6];
plot(x,y,'ro','markersize',3,'markerfacecolor','r')
grid on
xlabel('z')
ylabel('B')
title('Campo magnético producido por un imán')

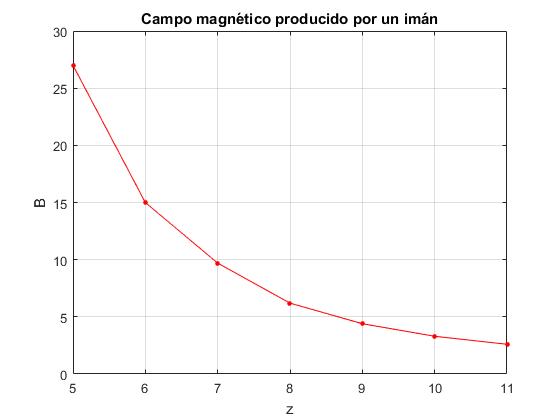
Un imán es un dipolo magnético y el campo producido en P es de la forma B=k/zⁿ. Queremos determinar el exponente n, para ello medimos con el sensor de campo magnético el campo B producido por el imán en varias posiciones z.

La posición z del sensor deberá estar suficientemente alejada del imán para que se cumpla la aproximación L<<z y por otra parte, el sensor no debería alejarse demasiado, para evitar que el campo magnético terrestre del orden de 10^-5 T, influya suficientemente en la medida

${\displaystyle \begin{array}{l}B=\frac{k}{z^n}\\ \log (B)=\log (k)-n\log (z)\end{array}}$

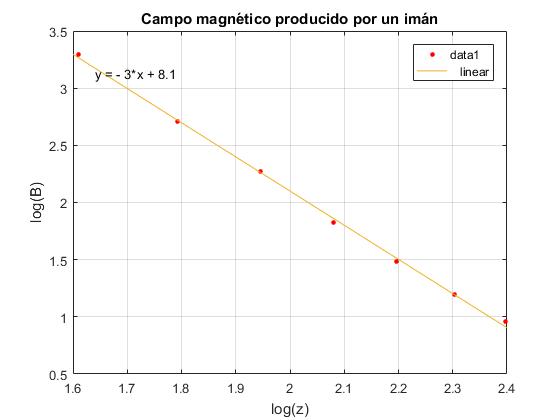
La recta de ajuste a los pares de datos (log(z), log(B)) tiene pendiente -n. El exponente cambiado de signo de la ley con la que varía el campo magnético con la distancia z al imán

 x=[5,6,7,8,9,10,11];
 y=[27,15,9.7,6.2,4.4,3.3,2.6];
 plot(log(x),log(y),'ro','markersize',3,'markerfacecolor','r')
 grid on
 xlabel('log(z)')
 ylabel('log(B)')
 title('Campo magnético producido por un imán')

Corremos el script y aparece la ventana gráfica con la representación de los datos como puntos de color rojo. En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p₁ y p₂ del polinomio (recta) y=p₁·x+p₂ de ajuste. El coeficente p₁=-2.9892, que es un valor próximo a -3.

Fuerza de atracción o repulsión entre dos imanes

Consideremos dos imanes cilíndricos coaxiales, separados una distancia d, entre sus planos meridianos. El inferior tiene radio a, altura h_a y momento magnético μ_a. El superior tiene radio b, altura h_b y momento magnético μ_b.

Dibujamos las corrientes superficiales equivalentes. Si el momento magnético del imán es μ y su radio a, la corriente equivalente I_eq que produce este momento magnético es I_eq=μ/(πa²)

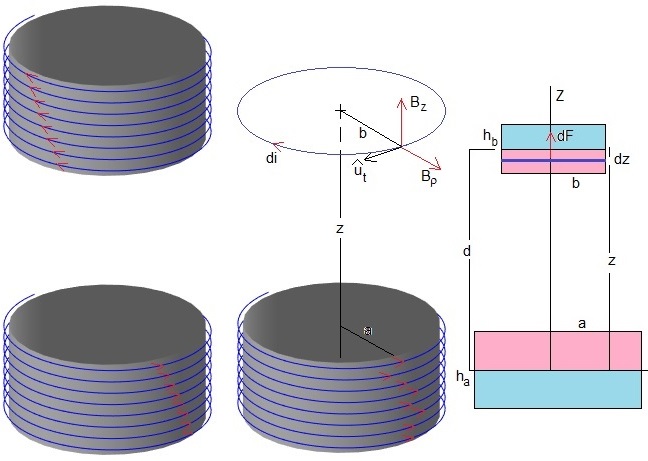
Calculamos las componentes B_z y B_ρ en el punto (b,z) del campo magnético producido por el imán inferior, equivalente a un solenoide de N espiras por las que circula una corriente i tal que, Ni=I_eq

${\displaystyle \begin{array}{l}{B}_{\rho }=B_0\left\{{\alpha }_{+}C(k_{+}\mathrm{,1,1,}-1)-{\alpha }_{-}C(k_{-}\mathrm{,1,1,}-1)\right\}\\ B_z=B_0\frac{a}{a+\rho }\left\{{\beta }_{+}C(k_{+},{\gamma }^2\mathrm{,1,}\gamma )-{\beta }_{-}C(k_{-},{\gamma }^2\mathrm{,1,}\gamma )\right\}\\ B_0=\frac{{\mu }_0}{\pi }ni=\frac{{\mu }_0}{\pi }\frac{I_{eq}}{h_a}=\frac{{\mu }_0}{\pi }\frac{{\mu }_a}{\pi a^2{h}_a}\\ z_{\pm }=z\pm \frac{h_a}{2}\\ k_{\pm }^2=\frac{z_{\pm }^2+{\left(a-\rho \right)}^2}{z_{\pm }^2+{\left(a+\rho \right)}^2}\\ {\alpha }_{\pm }=\frac{a}{\sqrt{z_{\pm }^2+{\left(\rho +a\right)}^2}}\\ {\beta }_{\pm }=\frac{z_{\pm }}{\sqrt{z_{\pm }^2+{\left(\rho +a\right)}^2}}\\ \gamma =\frac{a-\rho }{a+\rho }\end{array}}$

La fuerza que ejerce este campo magnético sobre una espira equivalente del imán superior por el que circula una corriente di, en el sentido indicado en la figura, es.

${\displaystyle \overrightarrow{dF}=di\left(\widehat{u_t}\times \overrightarrow{B}\right)2\pi b}$

• La componente B_z del campo magnético producido por el imán inferior, ejerce una fuerza cuya dirección es radial y sentido hacia el eje del imán. La fuerza neta se anula por simetría.

• La componente B_ρ del campo magnético producido por el imán inferior, ejerce una fuerza cuya dirección es paralela al eje Z y hacia arriba (si los imanes se repelen y hacia abajo si se atraen)

${\displaystyle d{F}_z=di(1·B_{\rho }\sin 90)2\pi b=2\pi b·B_{\rho }{I}_{eq}\frac{dz}{h_b}=2\pi b·B_{\rho }\frac{{\mu }_b}{\pi b^2}\frac{dz}{h_b}=2\frac{{\mu }_b}{b{h}_b}{B}_{\rho }·dz}$

La fuerza total F_z ejercida el campo magnético producido por el imán inferior sobre las corrientes superficiales equivalentes del imán superior es la suma

${\displaystyle F_z=2\frac{{\mu }_b}{b{h}_b}{\displaystyle \underset{d-h_b/2}{\overset{d+h_b/2}{\int }}{B}_{\rho }(z)dz}}$

En la página titulada Componentes del campo magnético producido por un solenoide se proporciona el código las funciones integral_eliptica y calcula_campo para calcular la componente B_ρ del campo magnético producido por un solenoide de radio a y altura h_a en un punto de coordenadas (ρ, z)

Para calcular la fuerza, empleamos el procedimiento de Simpson

function suma=simpson(f,x0,xf,n)
%n número par de intervalos, n+1 número de puntos en el vector    
    x=linspace(x0,xf,n+1);   
    h=x(2)-x(1);
    suma=f(x(1))+f(x(n+1));
    for i=2:2:n
        suma=suma+4*f(x(i));
    end
    for i=3:2:n-1
        suma=suma+2*f(x(i));
    end
    suma=suma*h/3;
end

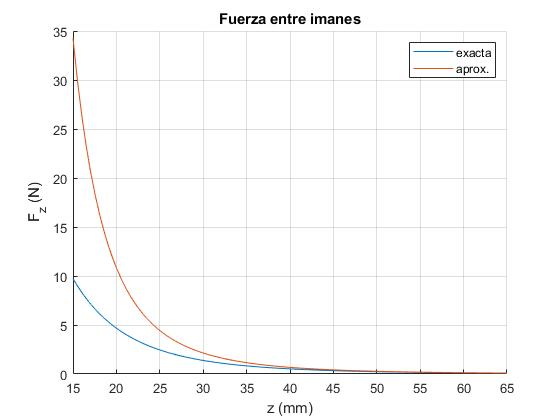
Representamos la fuerza F_z entre dos imanes iguales

• de radio a=b=10 mm
• altura h_a=h_b= 5 mm
• momento magnético μ_a=μ_b=1.7 A·m²

en función de la distancia d entre los planos meridianos de ambos imanes. Comparamos esta fuerza que denominamos 'exacta' con la aproximación, inversamente proporcional a la cuarta potencia de la distancia entre los dos imanes

a=10e-3; %radio
h=5e-3; %altura
mu=1.7; %momento magnético
B0=4*pi*1e-7*mu/(pi^2*a^2*h);
f=@(z) calcula_campo(a,h/2,a,z);
dd=(linspace(10,60,100)+5)/1000;
Fz=zeros(1,length(dd));
i=1;
for d=dd %distancia entre imanes
    Fz(i)=2*mu*B0*simpson(f,d-h/2, d+h/2, 50)/(a*h);
    i=i+1;
end
hold on
plot(dd*1000,Fz)
f=@(x) 6e-7*mu^2./x.^4; %aproxamación 1/x^4
plot(dd*1000,f(dd))
hold off
grid on
xlabel('z (mm)')
legend('exacta','aprox.')
ylabel('F_z (N)')
title('Fuerza entre imanes')

Medidas efectuadas en el laboratorio

En esta práctica de laboratorio, medimos la fuerza entre dos imanes permanentes. Colocamos dos imanes iguales uno sujeto por una pinza y el otro sobre una báscula. No lo ponemos directamente en el plato de la balanza electrónica, para que el potente campo magnético del imán no altere las medidas. El imán está sobre la balanza pero lejos de la balanza

Inicialmente, ponemos los dos imanes lejos uno del otro y taramos la balanza a cero

Se ha de tener cuidado de que las caras de los imanes sean paralelas y que estén alineados verticalmente. Sería conveniente, que se enfrentasen polos iguales de modo, que la fuerza fuese repulsiva. Con una regla medimos la distancia x entre las dos caras más próximas de los dos imanes y anotamos la medida de la fuerza F de interaccción en gramos que marca la balanza

Supondremos que la ley que mide la interacción entre los dos imanes responde a la fórmula.

${\displaystyle F=\frac{k}{x^n}}$

x=[3.5,5,7,9.5,11,13];
y=[50.7,29.2,7.3,2.5,1.2,0.4];
hold on
plot(x,y,'ro','markersize',3,'markerfacecolor','r')
fplot(@(x) exp(8.9405)./x.^4,[3.5,13])
hold off
grid on
xlabel('x')
ylabel('F')
title('Fuerza entre dos imanes')

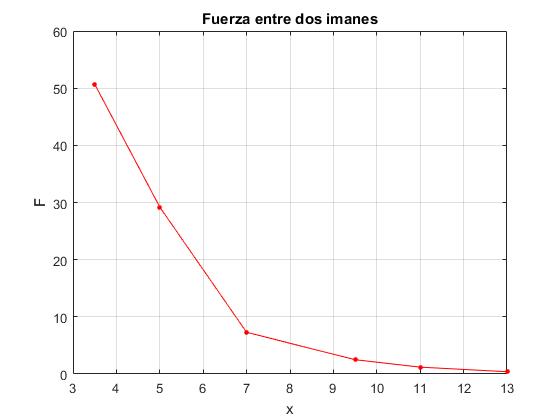
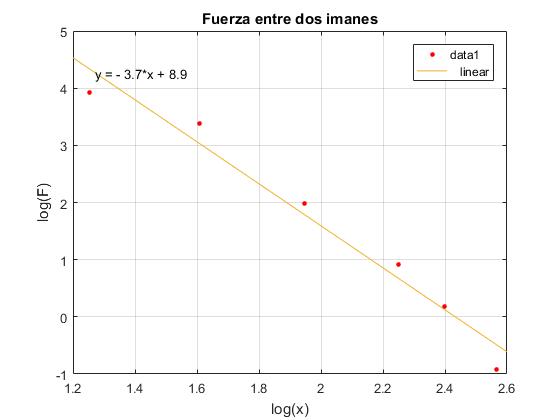
Comprobaremos que el exponente n de la ley de fuerza es próximo a cuatro.

x=[3.5,5,7,9.5,11,13];
y=[50.7,29.2,7.3,2.5,1.2,0.4];
plot(log(x),log(y),'ro','markersize',3,'markerfacecolor','r')
grid on
xlabel('log(x)')
ylabel('log(F)')
title('Fuerza entre dos imanes')

Corremos el script y aparece la ventana gráfica con la representación de los datos como puntos de color rojo. En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p₁ y p₂ del polinomio (recta) y=p₁·x+p₂ de ajuste. El coeficente p₁=-3.6743, que es un valor próximo a -4.

Para realizar esta práctica sería necesario disponer de un dispositivo que midiera con mayor precisión la distancia entre los dos imanes perfectamente alineados. Véase el segundo artículo citado en las referencias.

Referencias

Ramón Castañer, José M. Medina, María J. Cuesta-Bolao. The magnetic dipole interaction as measured by spring dynamometers. Am. J. Phys. 74 (6) June 2006. pp. 510-513

Manuel I González. Forces between permanent magnets: experiments and model. Eur. J. Phys. 38 (2017) 025202