Hemos estudiado la fuerza entre dos corrientes rectilíneas indefinidas, paralelas separadas una distancia d. Cuando las corrientes circulan en el mismo sentido, la fuerza es atractiva y cuando las corrientes circulan en sentido contrario la fuerza es repulsiva. Hemos supuesto que el radio de la sección de las corrientes es muy pequeña comparada con la distancia d de separación entre las mismas.

y que las dimensiones de la sección son comparables con la separación d entre las mismas.

Corriente de sección rectangular

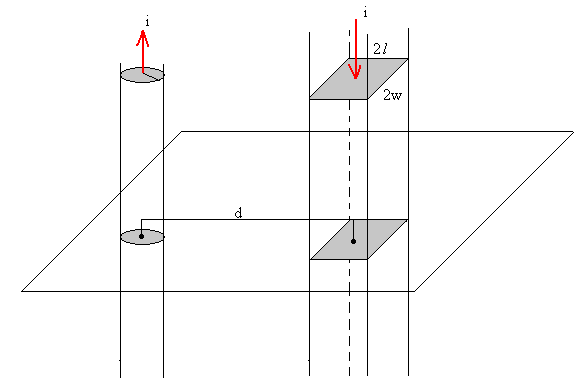
El campo producido por una corriente rectilínea indefinida i, para distancias mayores que el radio de la sección circular, es.

${\displaystyle B=\frac{{\mu }_{0}i}{2\pi r}}$

Vamos a calcular la fuerza que ejerce dicho campo sobre una corriente rectilínea indefinida de sección rectangular de dimensiones 2l (largo)y 2w (ancho), distante d.

Primero calculamos la fuerza que dicho campo ejerce sobre un elemento de corriente de dimensiones dx y dy.

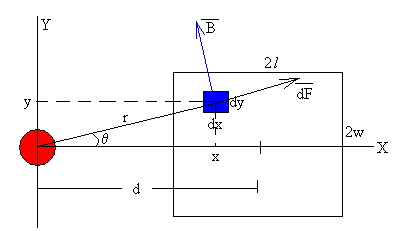
Suponiendo que la intensidad i está uniformemente distribuida en toda la sección rectangular, la corriente que circula por dicha sección infinitesimal (en color azul) es

${\displaystyle i\frac{dx·dy}{2l·2w}}$

La fuerza sobre una porción de corriente rectilínea indefinida de longitud L

${\displaystyle \overrightarrow{dF}=i\frac{dx·dy}{2l·2w}({\widehat{u}}_t\times \overrightarrow{B})L}$

• cuyo módulo es ${\displaystyle dF=i\frac{dx·dy}{2l·2w}\frac{{\mu }_{0}i}{2\pi r}L}$

• dirección es radial

• sentido, hacia fuera, si las corrientes tiene sentido contrario (se repelen)

Las componentes de dicha fuerza son:

dF_x=dFcosθ
dF_y=dFsinθ

Por simetría, las componentes dF_y se anulan de dos en dos, la fuerza resultante tiene la dirección del eje X

$$\begin{gathered} {\displaystyle d{F}_x=i\frac{dx·dy}{2l·2w}\frac{{\mu }_{0}i}{2\pi r}L\cos \theta =\left(\frac{{\mu }_{0}L{i}^2}{2\pi }\right)\frac{1}{2l·2w}\frac{dx·dy}{\sqrt{x^2+y^2}}\frac{x}{\sqrt{x^2+y^2}}= \\ \left(\frac{{\mu }_{0}L{i}^2}{2\pi d}\right)\frac{d}{2l·2w}\frac{x·dx·dy}{x^2+y^2}} \end{gathered}$$

El término ente paréntesis corresponde a la fuerza entre dos corrientes rectilíneas indefinidas paralelas que distan d.

Para calcular la fuerza resultante F_x tendremos que calcular una integral doble

${\displaystyle F_x=\left(\frac{{\mu }_{0}L{i}^2}{2\pi d}\right)\frac{d}{2l·2w}{\displaystyle \underset{-w}{\overset{w}{\int }}dy{\displaystyle \underset{d-l}{\overset{d+l}{\int }}\frac{x·dx}{x^2+y^2}}}}$

La integral con respecto a x es inmediata

${\displaystyle {\displaystyle \underset{d-l}{\overset{d+l}{\int }}\frac{x·dx}{x^2+y^2}}={\frac{1}{2}\ln \left(x^2+y^2\right)|}_{d-l}^{d+l}=\frac{1}{2}\ln \left(\frac{{(d+l)}^2+y^2}{{(d-l)}^2+y^2}\right)}$

Ahora, tenemos que resolver la integral

${\displaystyle \frac{1}{2}{\displaystyle \underset{-w}{\overset{w}{\int }}\ln \left(\frac{{(d+l)}^2+y^2}{{(d-l)}^2+y^2}\right)}dy}$

Integramos por partes

${\displaystyle \begin{array}{l}u=\ln \left(\frac{a^2+y^2}{b^2+y^2}\right)du=\frac{2y(b^2-a^2)}{(b^2+y^2)(a^2+y^2)}\\ dv=dxv=x\\ {\displaystyle \int \ln \left(\frac{a^2+y^2}{b^2+y^2}\right)dy=}y\ln \left(\frac{a^2+y^2}{b^2+y^2}\right)-{\displaystyle \int \frac{2y^2(b^2-a^2)}{(b^2+y^2)(a^2+y^2)}}dx\end{array}}$

Descomponemos la integral racional en la suma de dos integrales, del siguiente modo

${\displaystyle \frac{2y^2(b^2-a^2)}{(b^2+y^2)(a^2+y^2)}=\frac{Ay+B}{(a^2+y^2)}+\frac{Cy+D}{(b^2+y^2)}}$

Resolvemos el sistema de cuatro ecuaciones con cuatro incógnitas

A=0, C=0, B=-2a², D=2b²

${\displaystyle \begin{array}{l}{\displaystyle \int \ln \left(\frac{a^2+y^2}{b^2+y^2}\right)dy=}y\ln \left(\frac{a^2+y^2}{b^2+y^2}\right)+{\displaystyle \int \frac{2a^2}{(a^2+y^2)}dy}-{\displaystyle \int \frac{2b^2}{(b^2+y^2)}}dy=\\ y\ln \left(\frac{a^2+y^2}{b^2+y^2}\right)+2a·\arctan \left(\frac{y}{a}\right)-2b\arctan \left(\frac{y}{b}\right)\end{array}}$

Una vez que tenemos la función integrando calculamos el valor de la integral definida.

${\displaystyle \begin{array}{l}\frac{1}{2}{\displaystyle \underset{-w}{\overset{w}{\int }}\ln \left(\frac{{(d+l)}^2+y^2}{{(d-l)}^2+y^2}\right)}dy=\frac{1}{2}{\left(y\ln \left(\frac{{(d+l)}^2+y^2}{{(d-l)}^2+y^2}\right)+2(d+l)·\arctan \left(\frac{y}{d+l}\right)-2(d-l)\arctan \left(\frac{y}{d-l}\right)\right)|}_{-w}^w=\\ =w\ln \left(\frac{d^2+l^2+w^2+2dl}{d^2+l^2+w^2-2dl}\right)+2(d+l)·\arctan \left(\frac{w}{d+l}\right)-2(d-l)\arctan \left(\frac{w}{d-l}\right)\end{array}}$

La fuerza resultante es

${\displaystyle \begin{array}{l}{F}_x=\left(\frac{{\mu }_{0}L{i}^2}{2\pi d}\right)·f\\ f=\frac{d}{4lw}\left\{w\ln \left(\frac{d^2+l^2+w^2+2dl}{d^2+l^2+w^2-2dl}\right)+2(d+l)·\arctan \left(\frac{w}{d+l}\right)-2(d-l)\arctan \left(\frac{w}{d-l}\right)\right\}\end{array}}$

La fuerza de atracción entre dos corrientes rectilíneas indefinidas, se ve afectada por un factor multiplicativo f que depende de las dimensiones (w, l) de sección rectangular de la corriente y de su separación d de la corriente rectilínea que produce el campo magnético.

Corriente de sección circular

Calculamos ahora, la fuerza sobre una corriente indefinida de sección circular de radio R, que dista d de la corriente rectilínea indefinida que produce el campo magnético, ambas conducen la misma intensidad i pero en sentidos contrarios.

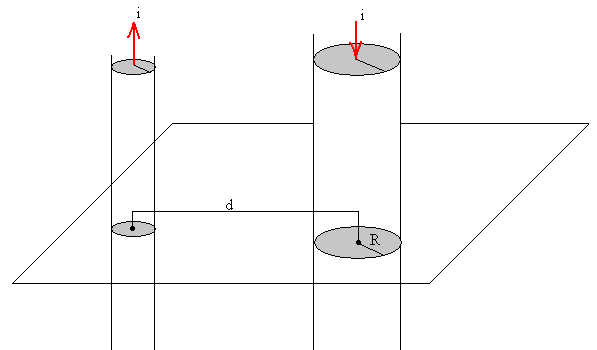
El campo producido por una corriente rectilínea indefinida i, es.

${\displaystyle B=\frac{{\mu }_{0}i}{2\pi r}}$

Vamos a calcular la fuerza que ejerce dicho campo sobre la corriente de sección circular de radio R, que dista d de la corriente rectilínea.

Primero calculamos la fuerza que dicho campo ejerce sobre un elemento de corriente de dimensiones dx y dy.

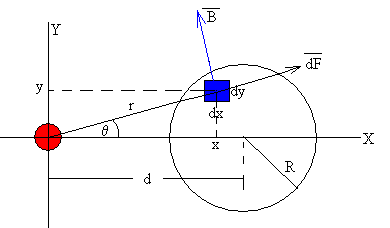
Suponiendo que la intensidad i está uniformemente distribuida en toda la sección circular, la corriente que circula por dicha sección infinitesimal es

${\displaystyle i\frac{dx·dy}{\pi R^2}}$

La fuerza sobre una porción de corriente rectilínea indefinida de longitud L

${\displaystyle \overrightarrow{dF}=i\frac{dx·dy}{\pi R^2}({\widehat{u}}_t\times \overrightarrow{B})L}$

• cuyo módulo es ${\displaystyle dF=i\frac{dx·dy}{\pi R^2}\frac{{\mu }_{0}i}{2\pi r}L}$

• dirección es radial

• sentido, hacia fuera, si las corrientes tiene sentido contrario (se repelen)

Las componentes de dicha fuerza son:

dF_x=dFcosθ
dF_y=dFsinθ

Por simetría, las componentes dF_y se anulan de dos en dos, la fuerza resultante tiene la dirección del eje X

$$\begin{gathered} {\displaystyle d{F}_x=i\frac{dx·dy}{\pi R^2}\frac{{\mu }_{0}i}{2\pi r}L\cos \theta =\left(\frac{{\mu }_{0}L{i}^2}{2\pi }\right)\frac{1}{\pi R^2}\frac{dx·dy}{\sqrt{x^2+y^2}}\frac{x}{\sqrt{x^2+y^2}}= \\ \left(\frac{{\mu }_{0}L{i}^2}{2\pi d}\right)\frac{d}{\pi R^2}\frac{x·dx·dy}{x^2+y^2}} \end{gathered}$$

El término ente paréntesis, corresponde a la fuerza entre dos corrientes rectilíneas indefinidas paralelas que distan d.

Para calcular la fuerza resultante F_x tendremos que calcular una integral doble

${\displaystyle F_x=\left(\frac{{\mu }_{0}L{i}^2}{2\pi d}\right)\frac{d}{\pi R^2}{\displaystyle \underset{-R}{\overset{R}{\int }}dy{\displaystyle \underset{x_1}{\overset{x_2}{\int }}\frac{x·dx}{x^2+y^2}}}}$

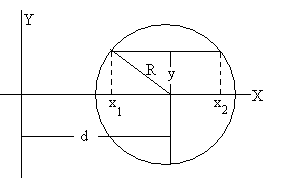
Manteniendo y constante, como en la figura, los límites de integración de x son x₁ y x₂

${\displaystyle x_1=d-\sqrt{R^2-y^2}{x}_2=d+\sqrt{R^2-y^2}}$

La integral con respecto a x es inmediata

$$\begin{gathered} {\displaystyle {\displaystyle \underset{x_1}{\overset{x_2}{\int }}\frac{x·dx}{x^2+y^2}}={\frac{1}{2}\ln \left(x^2+y^2\right)|}_{x_1}^{x_2}=\frac{1}{2}\ln \left(\frac{{\left(d+\sqrt{R^2-y^2}\right)}^2+y^2}{\left(d-\sqrt{R^2-y^2}\right)+y^2}\right)= \\ \frac{1}{2}\ln \left(\frac{d^2+R^2+2d\sqrt{R^2-y^2}}{d^2+R^2-2d\sqrt{R^2-y^2}}\right)} \end{gathered}$$

Ahora tenemos que resolver la integral

${\displaystyle \frac{1}{2}{\displaystyle \underset{-R}{\overset{R}{\int }}\ln \left(\frac{d^2+R^2+2d\sqrt{R^2-y^2}}{d^2+R^2-2d\sqrt{R^2-y^2}}\right)}dy}$

Hacemos el cambio de variable y=Rsinθ, dy=Rcosθ·dθ

${\displaystyle \frac{R}{2}{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}\ln \left(\frac{a+b\cos \theta }{a-b\cos \theta }\right)}\cos \theta ·d\theta }$

con a=d²+R² y b=2dR

Los nuevos límites de integración son –π/2 y π/2 que emplearemos para calcular la integral definida una vez conocida la función integrando. Integramos por partes

${\displaystyle \begin{array}{l}u=\ln \left(\frac{a+b\cos \theta }{a-b\cos \theta }\right)du=\frac{-2ab\sin \theta }{(a-b\cos \theta )(a+b\cos \theta )}d\theta \\ dv=\cos \theta ·d\theta v=\sin \theta \end{array}}$

El resultado es

${\displaystyle \frac{R}{2}{\displaystyle \int \ln \left(\frac{a+b\cos \theta }{a-b\cos \theta }\right)}\cos \theta ·d\theta =\frac{R}{2}\left\{\sin \theta ·\ln \left(\frac{a+b\cos \theta }{a-b\cos \theta }\right)+{\displaystyle \int \frac{2ab{\sin }^2\theta }{a^2-b^2{\cos }^2\theta }d\theta }\right\}}$

Para calcular la segunda integral, empleamos las relaciones trigonométricas

${\displaystyle \begin{array}{l}{\cos }^2\theta =\frac{1}{1+{\tan }^2\theta }{\text{sin}}^2\theta =\frac{{\tan }^2\theta }{1+{\tan }^2\theta }\\ \frac{R}{2}\left\{\sin \theta ·\ln \left(\frac{a+b\cos \theta }{a-b\cos \theta }\right)+{\displaystyle \int \frac{2ab{\tan }^2\theta }{a^2-b^2+a^2{\tan }^2\theta }d\theta }\right\}\end{array}}$

Para calcular la segunda integral, hacemos el cambio de variable, tanθ=t, dθ=dt/(1+t²)

${\displaystyle {\displaystyle \int \frac{2ab{\tan }^2\theta }{a^2-b^2+a^2{\tan }^2\theta }d\theta }={\displaystyle \int \frac{2ab{t}^2}{(a^2-b^2+a^2{t}^2)(1+t^2)}}dt}$

Es una integral racional que descomponemos en la suma de dos integrales, del siguiente modo

${\displaystyle \frac{2ab{t}^2}{(a^2-b^2+a^2{t}^2)(1+t^2)}=\frac{At+B}{(a^2-b^2+a^2{t}^2)}+\frac{Ct+D}{(1+t^2)}}$

En este sistema de cuatro ecuaciones con cuatro incógnitas

${\displaystyle \begin{array}{l}A=0C=0B=-2a\frac{a^2-b^2}{b}D=\frac{2a}{b}\\ {\displaystyle \int \frac{2ab{t}^2}{(a^2-b^2+a^2{t}^2)(1+t^2)}}dt=-\frac{2a}{b}(a^2-b^2){\displaystyle \int \frac{dt}{(a^2-b^2+a^2{t}^2)}}+\frac{2a}{b}{\displaystyle \int \frac{dt}{1+t^2}}\\ =-\frac{2\sqrt{a^2-b^2}}{b}\arctan \left(\frac{a}{\sqrt{a^2-b^2}}t\right)+\frac{2a}{b}\arctan (t)\end{array}}$

Deshacemos los cambios

${\displaystyle {\displaystyle \int \frac{2ab{\tan }^2\theta }{a^2-b^2+a^2{\tan }^2\theta }d\theta }=-\frac{2\sqrt{a^2-b^2}}{b}\arctan \left(\frac{a}{\sqrt{a^2-b^2}}\tan \theta \right)+\frac{2a}{b}\theta }$

Finalmente, la integral queda

${\displaystyle \begin{array}{l}\frac{R}{2}{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}\ln \left(\frac{a+b\cos \theta }{a-b\cos \theta }\right)}\cos \theta ·d\theta =\\ \frac{R}{2}\left\{{\sin \theta ·\ln \left(\frac{a+b\cos \theta }{a-b\cos \theta }\right)-\frac{2\sqrt{a^2-b^2}}{b}\arctan \left(\frac{a}{\sqrt{a^2-b^2}}\tan \theta \right)+\frac{2a}{b}\theta |}_{-\pi /2}^{\pi /2}\right\}=\\ \frac{R}{2}\left\{-\frac{2\sqrt{a^2-b^2}}{b}\pi +\frac{2a}{b}\pi \right\}\end{array}}$

Teniendo en cuenta que  a=d²+R² y b=2dR. La integral vale

${\displaystyle \frac{R}{2}\left\{-\frac{2(d^2-R^2)}{2dR}\pi +\frac{2(d^2+R^2)}{2dR}\right\}=\frac{\pi R^2}{d}}$

La resultante de las fuerzas que ejerce el campo magnético producido por la corriente rectilínea sobre los elementos diferenciales de la corriente de sección R es

${\displaystyle F_x=\left(\frac{{\mu }_{0}L{i}^2}{2\pi d}\right)\frac{d}{\pi R^2}{\displaystyle \underset{-R}{\overset{R}{\int }}dy{\displaystyle \underset{x_1}{\overset{x_2}{\int }}\frac{x·dx}{x^2+y^2}}}=\left(\frac{{\mu }_{0}L{i}^2}{2\pi d}\right)\frac{d}{\pi R^2}\frac{\pi R^2}{d}=\frac{{\mu }_{0}L{i}^2}{2\pi d}}$

La fuerza de atracción es la misma que la deducida para conductores rectilíneos indefinidos de pequeña sección  comparada con la separación d entre las corrientes paralelas.

Referencias

Fletcher K. A., Lyer S. V., Kinsey K. F. Some pivotal thoughts on the current balance. The Physics Teacher, Vol 41, May 2003, pp. 280-284