El campo magnético $\overrightarrow{B}$ creado por un circuito de forma cualesquiera recorrido por una corriente de intensidad i.

${\displaystyle \overrightarrow{B}=\frac{{\mu }_{0}i}{4\pi }{{\displaystyle \oint }}^{\text{}}\frac{{\widehat{u}}_t\times {\widehat{u}}_r}{r^2}dl}$

$\overrightarrow{B}$ es el vector campo magnético existente en un punto P del espacio, ${\widehat{u}}_t$ es un vector unitario cuya dirección es tangente al circuito y que nos indica el sentido de la corriente en la posición donde se encuentra el elemento dl. ${\widehat{u}}_r$ es un vector unitario que señala la posición del punto P respecto del elemento de corriente, la distancia entre ambos es r.

Sea una corriente plana de ecuación r=r(θ) en coordenadas polares

El campo magnético producido en el origen O es perpendicular al producto vectorial, ${\widehat{u}}_t\times {\widehat{u}}_r$ (ejeZ), es decir, plano de la corriente

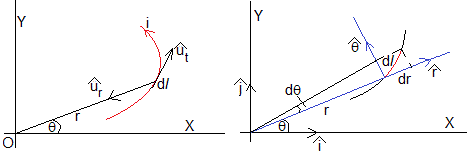
Como apreciamos en la figura de la derecha, el vector, ${\widehat{u}}_t·dl=dr·\widehat{r}+rd\theta ·\widehat{\theta }$, véase también la página titulada Ecuación de la trayectoria

El numerador es el producto vectorial

${\displaystyle {\widehat{u}}_t·dl\times {\widehat{u}}_r=\left(dr·\widehat{r}+rd\theta ·\widehat{\theta }\right)\times \left(-\widehat{r}\right)=-rd\theta \left(\widehat{\theta }\times \widehat{r}\right)=rd\theta ·\widehat{k}}$

La dirección del campo magnético es el eje Z, sentido positivo, si la corriente circula en sentido contario a las agujas del reloj. Su módulo es

${\displaystyle B=\frac{{\mu }_{0}i}{4\pi }{\displaystyle \oint \frac{d\theta }{r}}}$

Los ejemplos más sencillos son la corriente circular, rectilínea y la producida por una corriente en forma de sección cónica en uno de sus focos

Corriente circular

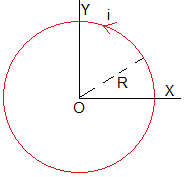
El campo magnético producido por una corriente circular de radio R en su centro, se obtiene fácilmente.

${\displaystyle B=\frac{{\mu }_{0}i}{4\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{d\theta }{R}}=\frac{{\mu }_{0}i}{2R}}$

Corriente rectilínea

El campo magnético producido en el origen O por una corriente rectilínea finita paralela al eje X, a una distancia d del mismo

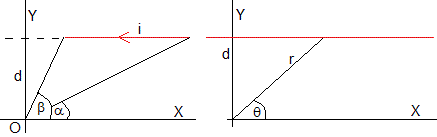
Como vemos en la figura de la derecha, la ecuación de la recta y=d es r=d/sinθ

${\displaystyle B=\frac{{\mu }_{0}i}{4\pi }{\displaystyle \underset{\alpha }{\overset{\beta }{\int }}\frac{\sin \theta }{d}}d\theta =\frac{{\mu }_{0}i}{4\pi d}\left(\cos \alpha -\cos \beta \right)}$

Para una corriente rectilínea indefinida, α→0, β→π

${\displaystyle B=\frac{{\mu }_{0}i}{2\pi d}}$

En esa misma página, hemos calculado, el campo magnético producido por una porción de corriente de longitud finita

Corriente en forma de elipse

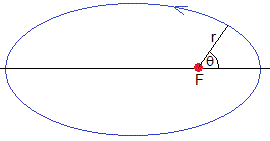
La ecuación de una cónica en coordenadas polares es

${\displaystyle r=\frac{d}{1+\epsilon \cos \theta }}$

Donde r es la distancia al foco F

Para una corriente en forma de elipse, el módulo del campo magnético en el foco F es

${\displaystyle B=\frac{{\mu }_{0}i}{4\pi }{\displaystyle \oint \frac{d\theta }{r}}=2\frac{{\mu }_{0}i}{4\pi }{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{(1+\epsilon \cos \theta )}{d}d\theta }=\frac{{\mu }_{0}i}{2d}}$

Corriente en forma de parábola

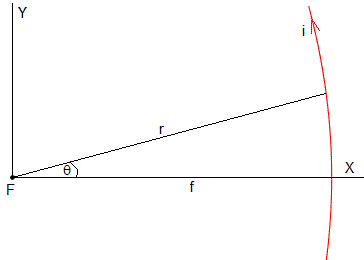
La excentricidad ε=1 y el resultado es idéntico a la elipse

Para θ=0, la distancia f entre el foco y el vértice, f=d/2

Corriente en forma de hipérbola

La corriente de forma hiperbólica tiene dos ramas, por lo que hemos de calcular el campo magnético producido por cada una de ellas en el foco F, tal como se muestra en la figura

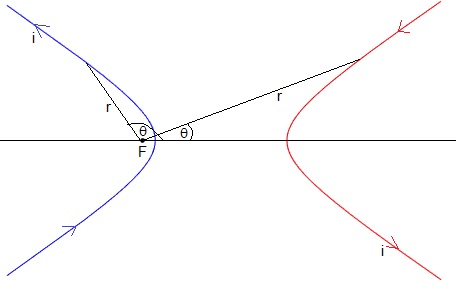
Para dibujar parte de la figura, se ha creado el script

d=1;
e=1.2; %excentricidad
hold on
r=@(th) d./(1+e*cos(th));
fplot(@(th) r(th).*cos(th),@(th) r(th).*sin(th),[-acos(-1/e)+0.2, acos(-1/e)-0.2]
,'color','b')
plot(0,0,'o','markersize',3,'markeredgecolor','k','markerfacecolor','k')
r=@(th) d./(-1+e*cos(th));
fplot(@(th) r(th).*cos(th),@(th) r(th).*sin(th),[-acos(1/e)+0.15,acos(1/e)-0.15]
,'color','r')
hold off
axis equal
axis off

• La ecuación de la rama izquierda es

${\displaystyle r=\frac{d}{1+\epsilon \cos \theta }}$

El ángulo de la asíntota (r→∞) es θ_i=arccos(-1/ε)

El campo magnético producido por la corriente en el foco F es por simetría, el doble

${\displaystyle B_i=2\frac{{\mu }_{0}i}{4\pi }{\displaystyle \underset{0}{\overset{{\theta }_i}{\int }}\frac{(1+\epsilon \cos \theta )}{d}d\theta }=\frac{{\mu }_{0}i}{2\pi d}\left({\theta }_i+\epsilon \sin {\theta }_i\right)}$

• La ecuación de la rama derecha es

${\displaystyle r=\frac{d}{-1+\epsilon \cos \theta }}$

El ángulo de la asíntota (r→∞) es θ_d=arccos(1/ε)

El campo magnético producido por la corriente en el foco F es de sentido contrario

${\displaystyle B_d=-2\frac{{\mu }_{0}i}{4\pi }{\displaystyle \underset{0}{\overset{{\theta }_d}{\int }}\frac{(-1+\epsilon \cos \theta )}{d}d\theta }=-\frac{{\mu }_{0}i}{2\pi d}\left(-{\theta }_d+\epsilon \sin {\theta }_d\right)}$

Como θ_i=π-θ_d

La suma de los dos campos en el foco F vale

${\displaystyle B=B_i+B_d=\frac{{\mu }_{0}i}{2d}}$

Campo magnético en el origen de una corriente en forma de sección cónica

Corriente elíptica

Calculamos el campo magnético producido en el origen O por una corriente de forma elíptica de semiejes a y b

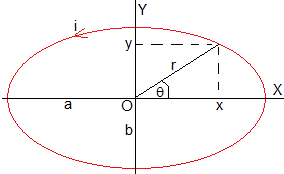
La ecuación de la elipse en coordendas rectangulares es

${\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$

Alternativamente, de la forma r=r(θ)

${\displaystyle \frac{r^2{\cos }^2\theta }{a^2}+\frac{r^2{\sin }^2\theta }{b^2}=1}$

Despejando la distancia r

${\displaystyle r^2=\frac{a^2{b}^2}{a^2{\sin }^2\theta +b^2{\cos }^2\theta }}$

El módulo del campo magnético en O producido por la espira elíptica es cuatro veces el producido por el arco comprendido en el primer cuadrante, 0≤θ<π/2

${\displaystyle B=\frac{{\mu }_{0}i}{4\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{\sqrt{a^2{\sin }^2\theta +b^2{\cos }^2\theta }}{ab}}d\theta =\frac{{\mu }_{0}i}{4\pi a}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\sqrt{1-\frac{b^2-a^2}{b^2}{\sin }^2\theta }}·d\theta =\frac{{\mu }_{0}i}{\pi a}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\sqrt{1-k^2{\sin }^2\theta }}·d\theta }$

En terminos de la integral elíptica completa de segunda especie

${\displaystyle B=\frac{{\mu }_{0}i}{\pi a}E(k),k^2=1-\frac{a^2}{b^2},b>a}$

ya que 0≤k≤1

Casos particulares

Cuando a→b, k→0, E(0)=π/2.

>> [K,E]=ellipke(0)
K =    1.5708
E =    1.5708  %es pi/2

${\displaystyle B=\frac{{\mu }_{0}i}{2a}}$

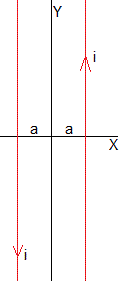
Es el campo magnético producido en el centro de una espira circular de radio a

Cuando b→∞ para un valor de a fijado, k=1

${\displaystyle B=\frac{{\mu }_{0}i}{\pi a}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\sqrt{1-{\sin }^2\phi }}·d\phi =\frac{{\mu }_{0}i}{\pi a}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\cos \phi }·d\phi =\frac{{\mu }_{0}i}{\pi a}}$

Es el campo magnético producido en el origen O por dos hilos indefinidos paralelos que conducen corrientes en sentido contrario y que distan a del eje Y

Corriente en forma de hipérbola

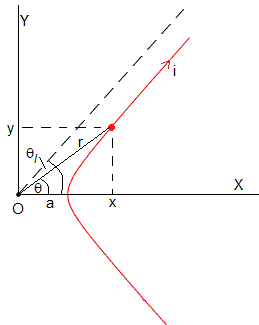
Calculamos el módulo del campo magnético en el origen O de una corriente en forma de hipérbola.

Partimos de la ecuación de la hipérbola en coordenadas rectangulares. Seguimos los mismos pasos que para una corriente en forma de elipse

${\displaystyle \begin{array}{l}\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\\ \frac{r^2{\cos }^2\theta }{a^2}-\frac{r^2{\sin }^2\theta }{b^2}=1\\ r^2=\frac{a^2{b}^2}{b^2{\cos }^2\theta -a^2{\sin }^2\theta }\end{array}}$

Cuando θ=0, r=a es la distancia del vértice de la hipérbola al origen O.

Sea θ_l el ángulo de la asíntota (línea a trazos) a la hipérbola. Cuando r→∞, bcosθ=asinθ, tanθ_l=b/a

${\displaystyle B=2\frac{{\mu }_{0}i}{4\pi }{\displaystyle \underset{0}{\overset{{\theta }_l}{\int }}\frac{\sqrt{b^2{\cos }^2\theta -a^2{\sin }^2\theta }}{ab}}d\theta =\frac{{\mu }_{0}i}{2\pi a}{\displaystyle \underset{0}{\overset{{\theta }_l}{\int }}\sqrt{1-\frac{b^2+a^2}{b^2}{\sin }^2\theta }}·d\theta =\frac{{\mu }_{0}i}{2\pi a}{\displaystyle \underset{0}{\overset{{\theta }_l}{\int }}\sqrt{1-k^2{\sin }^2\theta }}·d\theta }$

En este caso k>1, el resultado no es una integral elíptica incompleta. Buscamos en las tablas de integrales (Referencia 3), 2.595, n°2

${\displaystyle \begin{array}{l}{\displaystyle \int \sqrt{1-p^2{\sin }^{2}x}}·dx=pE\left(\alpha ,\frac{1}{p}\right)-\frac{p^2-1}{p}K\left(\alpha ,\frac{1}{p}\right)\\ \sin \alpha =p\sin x\end{array}}$

El módulo del campo magnético es

${\displaystyle B={\frac{{\mu }_{0}i}{2\pi a}\left\{kE\left(\alpha ,\frac{1}{k}\right)-\frac{k^2-1}{k}K\left(\alpha ,\frac{1}{k}\right)\right\}|}_0^{{\theta }_l}}$

Evaluamos la integral para el límite superior θ_l

${\displaystyle \sin \alpha =k\frac{\tan {\theta }_l}{\sqrt{1+{\tan }^2{\theta }_l}}=\sqrt{\frac{b^2+a^2}{b^2}}\frac{\frac{b}{a}}{\sqrt{1+\frac{b^2}{a^2}}}=\mathrm{1,}\alpha =\frac{\pi }{2}}$

Para el límite inferior, α=0, E(0,1/k)=0 y K(0,1/k)=0. El resultado es

${\displaystyle B=\frac{{\mu }_{0}i}{2\pi a}\left\{kE\left(\frac{1}{k}\right)-\frac{k^2-1}{k}K\left(\frac{1}{k}\right)\right\}}$

Donde E(1/k) y K(1/k) son integrales elípticas completas ya que α=π/2

Casos particulares

Cuando b→∞, k→1, θ_l→π/2. Obtenemos el campo magnético producido por una corriente rectilínea indefinida distante a del origen

${\displaystyle B=\frac{{\mu }_{0}i}{2\pi a}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\cos \theta }·d\theta =\frac{{\mu }_{0}i}{2\pi a}}$

Corriente en forma de estrella de n puntas

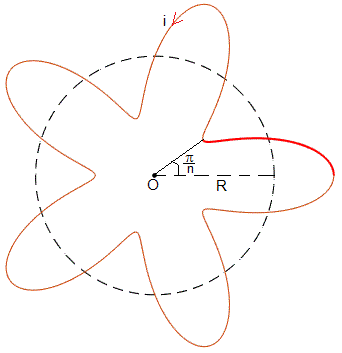
Consideremos la corriente descrita por la función r=r(θ)

${\displaystyle r=R\left(1+\epsilon \cos \left(n\theta \right)\right)}$

Para dibujar parte de la figura, se ha creado el script

n=5;
R=1;
ex=0.5;
hold on
fplot(@(x) R*cos(x), @(x) R*sin(x),[0,2*pi],'lineStyle','--','color','k')
fplot(@(x) R*(1+ex*cos(n*x)).*cos(x), @(x) R*(1+ex*cos(n*x)).*sin(x),[0,2*pi])
fplot(@(x) R*(1+ex*cos(n*x)).*cos(x), @(x) R*(1+ex*cos(n*x)).*sin(x),
[0,pi/n],'color','r','lineWidth',1.5)
plot(0,0,'ok', 'markersize',3,'markerfacecolor','k')
hold off
axis equal
axis off

Vamos a calcular el módulo del campo magnético en el origen O

Por simetría, solamente tenemos que calcular el campo magnético producido por la porción de corriente comprendida entre θ=0 y θ=π/n y multiplicar el resultado por 2n porciones

${\displaystyle B=\frac{{\mu }_{0}i}{4\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{d\theta }{R\left(1+\epsilon \cos \left(n\theta \right)\right)}}=2n\frac{{\mu }_{0}i}{4\pi R}{\displaystyle \underset{0}{\overset{\pi /n}{\int }}\frac{d\theta }{1+\epsilon \cos \left(n\theta \right)}}=\frac{{\mu }_{0}i}{2\pi R}{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{dx}{1+\epsilon \cos x}}}$

Donde se ha hecho el cambio de variable x=nθ. Buscamos la integral, 2.553, n° 3 (primera solución) a²>b²

${\displaystyle {\displaystyle \int \frac{dx}{a+b\cos x}}=\frac{2}{\sqrt{a^2-b^2}}\arctan \left(\frac{(a-b)\tan \left(\frac{x}{2}\right)}{\sqrt{a^2-b^2}}\right),a^2>b^2}$

El resultado es

${\displaystyle B=\frac{{\mu }_{0}i}{2\pi R}\left\{\frac{2}{\sqrt{1-{\epsilon }^2}}\arctan \left(\frac{(1-\epsilon )\tan \left(\frac{\pi }{2}\right)}{\sqrt{1-{\epsilon }^2}}\right)\right\}=\frac{{\mu }_{0}i}{\pi R}\frac{\arctan \left(\infty \right)}{\sqrt{1-{\epsilon }^2}}=\frac{{\mu }_{0}i}{2R}\frac{1}{\sqrt{1-{\epsilon }^2}}}$

Corriente en forma de espiral

Vamos a calcular el módulo del campo magnético en O producido por una corriente en forma de espiral, r=aexp(pθ)

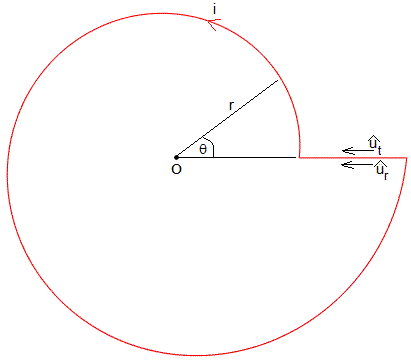
Para dibujar parte de la figura, se ha creado el script

p=0.1;
a=1;
hold on
fplot(@(x) a*exp(p*x).*cos(x), @(x) a*exp(p*x).*sin(x),[0,2*pi],'color','r')
line([a,a*exp(p*2*pi)],[0,0],'color','r')
plot(0,0,'ok', 'markersize',3,'markerfacecolor','k')
hold off
axis equal
axis off

El campo magnético producido en el origen O por el segmento recto es nulo, ya que los vectores unitarios tienen la misma dirección, el producto vectorial es nulo, ${\widehat{u}}_t\times {\widehat{u}}_r=0$

${\displaystyle B=\frac{{\mu }_{0}i}{4\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{d\theta }{a{e}^{p\theta }}}=\frac{{\mu }_{0}i}{4\pi a}\frac{1-e^{-2\pi p}}{p}}$

Casos particulares

Cuando p→0, aplicando la regla de L'Hôpital

>> syms p;
>> limit((1-exp(-2*pi*p))/p,p,0)
ans =2*pi

El módulo del campo magnético en O es el de una corriente circular de radio a en su centro

${\displaystyle B=\frac{{\mu }_{0}i}{2a}}$

Corriente en forma de epicicloide o hipocicloide

En la página titulada 'Curvas cicloidales' se representan hipocicloides y epicicloides para distintos valores del cociente m/n

En esta sección, nos limitaremos a las curvas cicloidales para las que n=1 y h=b. Las ecuaciones paramétricas de dichas curvas serán entonces

${\displaystyle \{\begin{array}{l}x=a\left(1+\frac{\delta }{m}\right)\cos \theta -\frac{\delta }{m}a\cos \left((m+\delta )\theta \right)\\ y=a\left(1+\frac{\delta }{m}\right)\sin \theta -\frac{1}{m}a\sin \left((m+\delta )\theta \right)\end{array}\{\begin{array}{l}\delta =\mathrm{1,}\text{epiciloide}\\ \delta =-\mathrm{1,}\text{hipocicloide}\end{array}}$

Representamos dos de estas curvas, para m=5 y a=1.

a=1; 
m=5;
hold on
delta=1;
x=@(t) a*(1+delta/m)*cos(t)-delta*a*cos((m+delta)*t)/m;
y=@(t) a*(1+delta/m)*sin(t)-a*sin((m+delta)*t)/m;
fplot(x,y,[0,2*pi])
fplot(x,y,[0,pi/m], 'lineWidth',1.5, 'color','b')

delta=-1;
x=@(t) a*(1+delta/m)*cos(t)-delta*a*cos((m+delta)*t)/m;
y=@(t) a*(1+delta/m)*sin(t)-a*sin((m+delta)*t)/m;
fplot(x,y,[0,2*pi])
fplot(x,y,[0,pi/m], 'lineWidth',1.5, 'color','r')
hold off
axis equal
xlabel('x')
ylabel('y')
grid on
title('Curvas cicloidales')

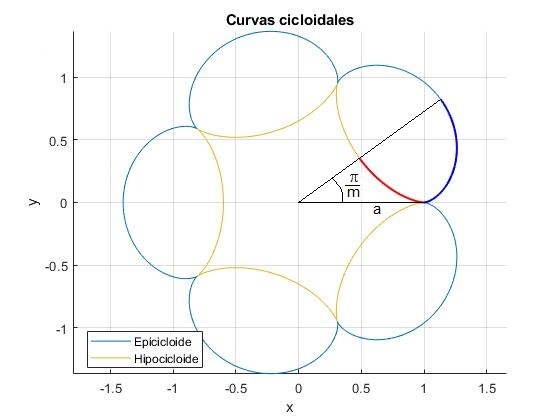
Supongamos un conductor plano que lleva una corriente i y cuya forma es una curva hipocicloide o epicicloide. El campo magnético producido en el origen por dicha corriente es, por simetría, m veces el campo magnético producido por el segmento de curva comprendido entre 0 y 2π/m. A su vez, por razón de simetría, éste es el doble del producido por el segmento comprendido entre 0 y π/m señalado mediante una línea gruesa en la figura

Nos daremos cuenta, que el campo magnético producido por el hipocicloide (curva de color amarillo) será mayor que el producido por el epicicloide (curva de color azul claro) al estar esta corriente más alejada en promedio del origen.

${\displaystyle \begin{array}{l}B=\frac{{\mu }_{0}i}{4\pi }{\displaystyle \oint \frac{d\theta }{r}}=\frac{{\mu }_{0}i}{4\pi }m{\displaystyle \underset{0}{\overset{2\pi /m}{\int }}\frac{d\theta }{r}}=\frac{{\mu }_{0}i}{2\pi }m{\displaystyle \underset{0}{\overset{\pi /m}{\int }}\frac{d\theta }{r}}\\ r=\sqrt{x^2+y^2}=a\sqrt{{\left(1+\frac{\delta }{m}\right)}^2+\frac{1}{m^2}-2\frac{\delta }{m}\left(1+\frac{\delta }{m}\right)\cos \left(m\theta \right)}\end{array}}$

Haciendo el cambio de variable x=m·θ, dx=m·dθ

${\displaystyle B=\frac{{\mu }_{0}i}{2\pi a}{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{dx}{\sqrt{{\left(1+\frac{\delta }{m}\right)}^2+\frac{1}{m^2}-2\frac{\delta }{m}\left(1+\frac{\delta }{m}\right)\cos x}}}}$

Buscamos una integral similar en el libro titulado Table of Integrals, Series, and Products, véase las referencias. La encontramos en el apartado 2.571, n° 5 y 4 (primera solución, pág. 179

• Epicicloide, δ=1

${\displaystyle a=1+\frac{2}{m}+\frac{2}{m^2},b=\frac{2}{m}+\frac{2}{m^2},a>b>0}$

Le corresponde la integral, n° 5

${\displaystyle {\displaystyle \int \frac{dx}{\sqrt{a-b\cos x}}}=\frac{2}{\sqrt{a+b}}F\left(\gamma ,r\right)\{\begin{array}{l}\gamma =\arcsin \sqrt{\frac{(a+b)(1-\cos x)}{2(a-b\cos x)}}\\ r=\sqrt{\frac{2b}{a+b}}\end{array}}$

Evaluamos la integral para el límite superior x=π, γ=π/2 y para el límite inferior x=0, γ=0

${\displaystyle \begin{array}{l}a+b={\left(1+\frac{2}{m}\right)}^2\\ r=\frac{\sqrt{2(m+1)}}{m+2}\end{array}}$

El campo magnético producido en el origen por una corriente en forma de epicicloide es perpendicular al plano de la corriente y su módulo es

${\displaystyle B=\frac{{\mu }_{0}i}{2\pi a}\frac{2m}{m+2}F\left(\frac{\pi }{2},\frac{\sqrt{2(m+1)}}{m+2}\right)=\frac{{\mu }_{0}i}{\pi a}\frac{m}{m+2}K\left(\frac{\sqrt{2(m+1)}}{m+2}\right)}$

• Hipocicloide, δ=-1

${\displaystyle a=1-\frac{2}{m}+\frac{2}{m^2},b=\frac{2}{m}-\frac{2}{m^2},a>b>0}$

Le corresponde la integral, n° 4, primera solución

${\displaystyle {\displaystyle \int \frac{dx}{\sqrt{a+b\cos x}}}=\frac{2}{\sqrt{a+b}}F\left(\frac{x}{2},r\right)\{r=\sqrt{\frac{2b}{a+b}}}$

Evaluamos la integral para el límite superior x=π y para el límite inferior x=0

${\displaystyle \begin{array}{l}a+b=1\\ r=\sqrt{2b}=\frac{2}{m}\sqrt{m-1}\end{array}}$

El campo magnético producido en el origen por una corriente en forma de hipocicloide es perpendicular al plano de la corriente y su módulo es

${\displaystyle B=\frac{{\mu }_{0}i}{\pi a}F\left(\frac{\pi }{2},\frac{2}{m}\sqrt{m-1}\right)=\frac{{\mu }_{0}i}{\pi a}K\left(\frac{2}{m}\sqrt{m-1}\right)}$

El campo magnético producido por una corriente circular de radio a, en su centro es B₀=μ₀i/(2a). Vamos a comprobar que cuando m se hace grande, el campo magnético producido por las corrientes cicloidades tienden al campo producido por una corriente circular, B/B₀→1. Representamos B/B₀ en función de m

m=2:2:200;
B1=2*m.*ellipke(2*(m+1)./(m+2).^2)./(pi*(m+2));%Epicicloide
B2=2*ellipke(4*(m-1)./m.^2)/pi; %Hipocicloide
hold on
plot(m,B1)
plot(m,B2)
hold off
grid on
legend('Epicicloide', 'Hipocicloide','location', 'best')
xlabel('m')
ylabel('B/B_0')
title('Campo magnético')

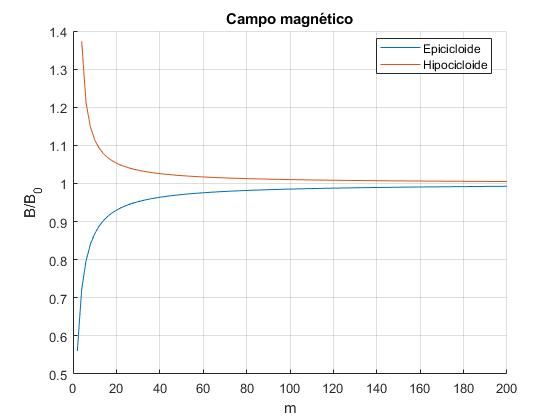
Como apreciamos, el campo producido por el hipocicloide es mayor, al estar más cerca del origen los distintos tramos de la corriente

Campo magnético producido por una espira de forma elíptica en un punto de su eje

Por simetría, el campo producido por una espira elíptica de semiejes a y b en un punto de su eje P(0, 0, z) solamente tiene componente a lo largo del eje Z, como en el caso de la espira circular.

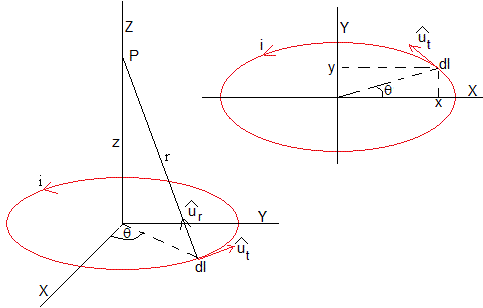
Aplicamos la ley de Biot

${\displaystyle \overrightarrow{B}=\frac{{\mu }_{0}i}{4\pi }{\displaystyle \oint \frac{{\widehat{u}}_t\times {\widehat{u}}_r}{r^2}}dl}$

Como vemos en la figura, la distancia r entre el elemento de corriente dl que está situado en el punto (x=acosθ, y=bsinθ, 0) y el punto P(0, 0, z) considerado es

${\displaystyle \begin{array}{l}{r}^2=a^2{\cos }^2\phi +b^2{\sin }^2\phi +z^2\\ {\widehat{u}}_r=\frac{-a·\cos \phi ·\widehat{i}-b·\sin \phi ·\widehat{j}+z·\widehat{k}}{r}\end{array}}$

Por otra parte

${\displaystyle {\widehat{u}}_t·dl=dx·\widehat{i}+dy·\widehat{j}=(-a\sin \theta ·\widehat{i}+b\cos \theta ·\widehat{j})d\theta }$

El producto vectorial

${\displaystyle \frac{{\widehat{u}}_t·dl\times {\widehat{u}}_r}{r^2}=\frac{1}{r}\left(bz\cos \theta ·\widehat{i}+az\sin \theta ·\widehat{j}+ab\widehat{k}\right)d\theta }$

Las componentes del campo magnético en P son

${\displaystyle \begin{array}{l}{B}_x=\frac{{\mu }_{0}i}{4\pi }bz{\displaystyle \oint \frac{\cos \theta }{r^3}}d\theta \\ B_y=\frac{{\mu }_{0}i}{4\pi }az{\displaystyle \oint \frac{\sin \theta }{r^3}}d\theta \\ B_z=\frac{{\mu }_{0}i}{4\pi }ab{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{d\theta }{{\left(a^2{\cos }^2\theta +b^2{\sin }^2\theta +z^2\right)}^{3/2}}}\end{array}}$

Solamente tenemos que calcular la componente B_z, por simetría las otras dos se anulan

Por otra parte, basta calcular el campo producido por el arco comprendido entre θ=0 y θ=π/2 y multiplicar el resultado por cuatro

${\displaystyle B_z=\frac{{\mu }_{0}i}{\pi }\frac{ab}{\sqrt{{\left(a^2+z^2\right)}^{3/2}}}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\theta }{{\left(1+\frac{b^2-a^2}{a^2+z^2}{\sin }^2\theta \right)}^{3/2}}}}$

Buscamos la solución a la integral, 2.598, n° 2

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{dx}{\sqrt{{\left(1+p^2{\sin }^{2}x\right)}^3}}}=\frac{1}{\sqrt{1+p^2}}E\left(\alpha ,\frac{p}{\sqrt{1+p^2}}\right)\\ \sin \alpha =\frac{\sqrt{1+p^2}\sin x}{\sqrt{1+p^2{\sin }^{2}x}}\end{array}}$

Cuando θ=x=0, entonces α=0. Cuando θ=π/2, sinα=1, α=π/2. Obtenemos una integral elíptica completa

La componente B_z del campo magnético producido por la espira de forma elíptica en P

${\displaystyle B_z=\frac{{\mu }_{0}i}{\pi }\frac{ab}{\left(a^2+z^2\right)\sqrt{b^2+z^2}}E\left(\sqrt{\frac{b^2-a^2}{b^2+z^2}}\right),0\le \frac{b^2-a^2}{b^2+z^2}\le 1}$

Cuando z=0, obtenemos el campo magnético B₀ en el centro de la espira de forma elíptica

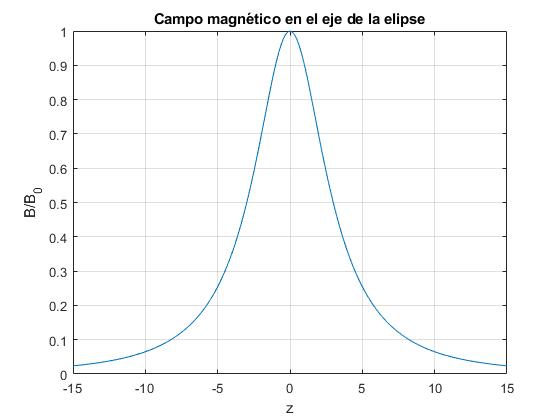
Representamos el cociente B_z/B₀ en función de z. Como la curva es simétrica, calculamos solamente para z≥0

${\displaystyle \frac{B_z}{B_0}=\frac{a^{2}b}{\left(a^2+z^2\right)\sqrt{b^2+z^2}}\frac{E\left(\sqrt{\frac{b^2-a^2}{b^2+z^2}}\right)}{E\left(\sqrt{\frac{b^2-a^2}{b^2}}\right)}}$

b=8; %semiejes
a=3;
z=linspace(0,15,100);
[~,Ez]=ellipke((b^2-a^2)./(b^2+z.^2));
[~,E0]=ellipke((b^2-a^2)./b^2);
B=a^2*b*Ez./((a^2+z.^2).*sqrt(b^2+z.^2)*E0);
plot([-fliplr(z),z],[fliplr(B),B])
xlabel('z')
ylabel('B/B_0')
grid on
title('Campo magnético en el eje de la elipse')

Referencias

José A. Miranda. Magnetic field calculation for arbitrarily shaped planar wires. Am. J. Phys. 68 (3), March 2000. pp. 254-258

C. Christodoulides. The magnetic field produced at a focus of a current-carrying conductor in the shape of a conic section. Am. J. Phys.77 (12), December 2009. pp. 1195-1196

David Romero-Abad. The magnetic field in the axis of an elliptic loop current. Phys. Educ. 56 (2021) 025014

I. S. Gradshteyn, I. M. Ryzhik. Table of Integrals, Series, and Products. Seventh Edition. Elsevier (2007). Integrales: 2.595, n°2. pág. 202. 2.553, n°3 (primera solución) pág. 172. 2.598, n°2, pág. 205. 2.571, n° 5 y 4 (primera solución), pág. 179

David Romero Abad. The Magnetic field for an n-cusped Epi and Hypo-Cycloids loop current. Revista Brasileira de Ensino de Física, vol. 43, e20200482 (2021) https://www.scielo.br/j/rbef/i/2021.v43/