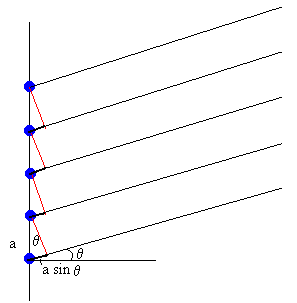
Consideremos ahora el caso de varias fuentes idénticas distribuidas linealmente, tal como se muestra en la figura. Supondremos también que deseamos examinar el estado del punto P situado a una distancia muy lejana comparada con la separación de las fuentes.

Cuando emite una sola fuente, el punto P describe un M.A.S. de amplitud A₁ y frecuencia angular ω. Cuando emiten N fuentes simultáneamente, el punto P describe un M.A.S. que es la composición de N M.A.S. de la misma dirección y frecuencia.

Calculamos la amplitud A resultante sumando vectorialmente las amplitudes correspondientes a cada una de las fuentes. Si todas las fuentes son iguales, sus vectores tienen la misma longitud A₁ y el ángulo δ entre dos vectores consecutivos es igual al producto del número de onda k por la diferencia de caminos a·sinθ entre dos fuentes consecutivas.

δ =ka·sinθ .

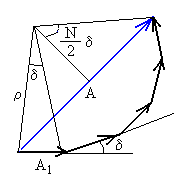
Calculamos cada uno de los lados A₁ del polígono y la amplitud resultante A.

${\displaystyle A=2\rho \sin \frac{N\delta }{2}{A}_1=2\rho \sin \frac{\delta }{2}}$

Siendo ρ el radio del polígono regular. Eliminando el radio ρ, expresamos la amplitud resultante A en función de la amplitud A₁ debida a cada una de las fuentes.

${\displaystyle A=A_1\frac{\sin \left(\frac{N}{2}\delta \right)}{\sin \left(\frac{1}{2}\delta \right)}}$

La intensidad que es proporcional al cuadrado de la amplitud

${\displaystyle I=I_0{\left(\frac{\sin \left(\frac{N}{2}\delta \right)}{\sin \left(\frac{1}{2}\delta \right)}\right)}^2=I_0{\left(\frac{\sin \left(\frac{N\pi a\sin \theta }{\lambda }\right)}{\sin \left(\frac{\pi a\sin \theta }{\lambda }\right)}\right)}^2}$

Alternativamente, con números complejos

La amplitud A es la suma de

${\displaystyle A=A_1+A_1{e}^{i\delta }+A_1{e}^{i2\delta }+\mathrm{...}+A_1{e}^{i(N-1)\delta }}$

de N términos de una progresión geométrica de razón r=e^iδ

${\displaystyle A=A_1\frac{1-e^{iN\delta }}{1-e^{i\delta }}}$

La intensidad que es proporcional al cuadrado de la amplitud

${\displaystyle I=I_0\frac{1-e^{iN\delta }}{1-e^{i\delta }}\frac{1-e^{-iN\delta }}{1-e^{-i\delta }}=I_0\frac{2-2\cos \left(N\delta \right)}{2-2\cos \delta }=I_0\frac{{\sin }^2\left(\frac{N\delta }{2}\right)}{{\sin }^2\left(\frac{\delta }{2}\right)}}$

La interferencia es constructiva cuando a·sinθ/λ=n, donde n es un número entero. Las ondas emitidas por las fuentes adyacentes están en fase. El numerador y el denominador de la expresión de la intensidad son ceros, el cociente es la unidad (regla de L'Hôpital) y la intensidad es máxima y proporcional al cuadrado del número de fuentes, I=N²I₀.

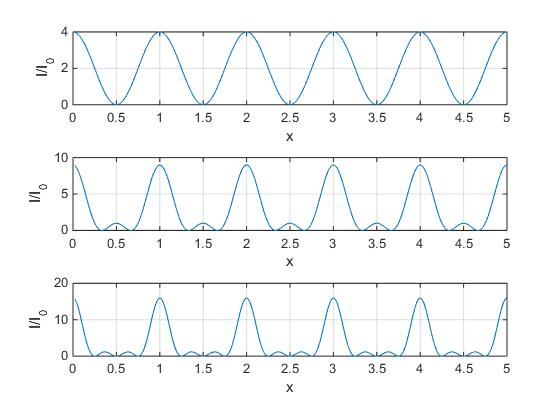
La intensidad es nula cuando el numerador es cero, pero no lo es el denominador. Por ejemplo, para N=4 los mínimos se producen para 4πa·sinθ/λ=π, 4πa·sinθ/λ=2π, 4πa·sinθ/λ=3π. Es decir, cuando a·sinθ/λ=1/4, a·sinθ/λ=1/2, a·sinθ/λ=3/4, tal como puede verse en la figura más abajo.

En general, los mínimos de intensidad se producen cuando a·sinθ/λ=n'/N. donde n' toma los valores de 1 a N-1, de N+1 a 2N-1, etc. Los valores n'=N, 2N ... se excluyen ya que hacen que el numerador y denominador sean cero simultáneamente, lo que corresponde a un máximo. Entre dos mínimos hay siempre un máximo, luego hay N-2 máximos adicionales entre los máximos principales. Sus valores son muy pequeños especialmente cuando N es grande.

En la figura, se muestra la representación gráfica de la intensidad en función de a·sinθ/λ, para N=2, 3 y 4. Los picos de la intensidad se van haciendo cada vez más estrechos a medida que aumenta el número de fuentes. Cuando N es grande, el movimiento ondulatorio resultante solamente es significativo para bandas estrechas alrededor de los ángulos θ tales que a·sinθ/λ=n.

En el código del script evitamos las indeterminaciones 0/0, mediante vectores lógicos. Cuando se produce el cociente 0/0, x=a·sinθ/λ es un número entero, la intensidad es proporcional a N² en caso contario la intensidad viene determinada por el cuadrado del cociente sin(Nπx)/sin(πx)

x=0:0.02:5;
for N=2:4
    subplot(3,1,N-1)
    y=N^2*((x-floor(x))<eps)+((x-floor(x))>eps).*(sin(N*pi*x).
/sin(pi*x)).^2;

    plot(x,y)
    xlabel('x')
    ylabel('I/I_0')
    grid on
end

Conocida la longitud de onda λ y la separación a determinamos los ángulos θ, para los cuales hay un máximo principal o un mínimo de intensidad.

Actividades

Se introduce

• El número N de fuentes, en el control titulado Número de fuentes

Se pulsa el botón titulado Nuevo

En la parte derecha se representa la intensidad en función de x=a·senθ/λ. En la parte inferior, se representa la intensidad mediante colores pertenecientes a la escala de grises. Podemos apreciar las típicas franjas claras y oscuras de los diagramas de interferencia y difracción.

En el control titulado Posición se establece la posición de observación. Se selecciona el control y con los cursores: izquierda y derecha se va moviendo el dedo de la barra de desplazamiento. Los vectores (en color azul) representan las amplitudes de las ondas procedentes de cada una de las fuentes con sus fases respectivas y el vector resultante (en color rojo) de la superposición de los M.A.S.

Cuando elegimos las posiciones de los máximos de intensidqad, todos los vectores tienen la misma dirección, la amplitud resultante es N veces la amplitud correspondiente a una de las fuentes y la intensidad es proporcional al cuadrado N² del número de fuentes

Cuando nos situamos en un mínimo, el origen del primer vector coincide con el extremo del último, la amplitud resultante es cero, la intensidad es nula.

Se proporciona el dato de la intensidad, para cada una de las direcciones, x=a·sinθ/λ tomando como intensidad máxima la unidad. Se sugiere comprobar que las posiciones de máxima y mínima intensidad para N=2, 3, 4, y 5 coinciden con las dadas por la fórmula.

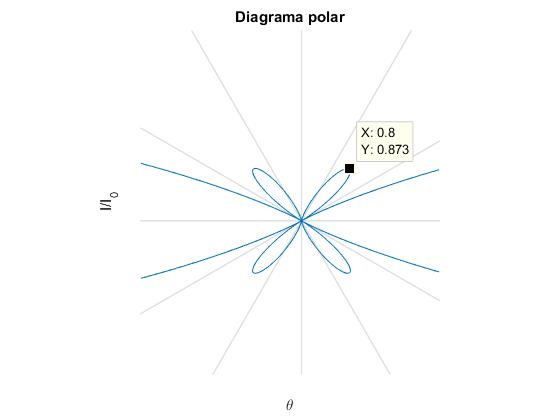
Diagrama polar

El diagrama polar es la representación de la intensidad en función del ángulo θ, nos permite ver la interferencia desde otra perspectiva.

Supongamos que tenemos N=4 fuentes separadas a=λ/2, media longitud de onda. Las direcciones para las cuales hay un máximo de intensidad son a·sinθ/λ=n, es decir, sinθ=2n. Solo es posible n=0, los máximos principales en las direcciones θ=0 y π. Los mínimos de intensidad se producen cuando a·sinθ/λ=n'/N, es decir, sinθ=n'/2. con n'=1, 2, 3, 5, 6...Solamente es posible n'=±1, y n'=±2, que corresponden a los ángulos θ=π/6 y π/2.

Cuando colocamos cuatro antenas separadas media longitud de onda, se transmite y se recibe la información preferentemente en la dirección perpendicular a la línea que une las fuentes.

angulo=-pi:pi/360:pi;
d=0.5;  %separación dividido por la longitud de onda
N=4;
x=pi*d*sin(angulo);
in=N^2*((x-floor(x))<eps)+((x-floor(x))>eps).*(sin(N*x)./sin(x)).^2;
polar(angulo,in)
xlabel('\theta')
ylabel('I/I_0')
title('Diagrama polar')

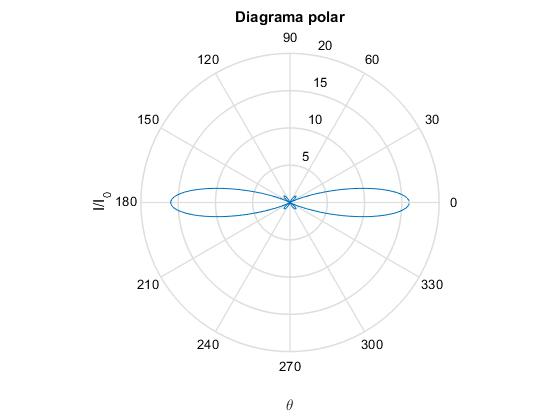
Si en el menú de la ventana gráfica, seleccionamos el icono Zoon In veremos con más detalle los mínimos secundarios. Con el icono Data cursor podemos conocer la dirección y la intensidad de los máximos secundarios

Actividades

Se introduce

• El cociente a/λ entre la separación entre las fuentes y la longitud de onda, en el control titulado Separación/l. onda.
• El número de fuentes, en el control titulado N. fuentes.

Se pulsa el botón titulado Nuevo

Se establece la escala de la representación gráfica, en el control titulado Escala

En la parte superior izquierda, se proporciona los datos de las direcciones que corresponden a los máximos principales.

Para ver los máximos secundarios, es necesario aumentar la escala de la representación gráfica.

Simulación

Se introduce

• La longitud de onda λ, en el control titulado L. onda
• El valor de la separación entre las fuentes a, en el control titulado Separación.
• el número de fuentes N, en el control titulado N. fuentes.

Se pulsa el botón titulado Nuevo.

Si seleccionamos 1 fuente, observamos las ondas circulares alrededor de la fuente (en color rojo). La distancia entre el centro de dos zonas claras consecutivas es una longitud de onda o la distancia entre el centro de dos zonas oscuras consecutivas.

Se cambia la longitud de onda y se observa la representación de las ondas circulares, pulsando el botón titulado Nuevo.

Si seleccionamos 2 fuentes, observamos la interferencia de las dos fuentes, en la figura de la izquierda, como si fuese una fotografía tomada en una cubeta de agua. En la figura de la derecha, se representa la intensidad en cada punto del plano. La máxima intensidad en color blanco y la mínima en color negro.

Para observar un diagrama similar al producido por la difracción de una rendija, que estudiaremos en la siguiente página, se introducen los siguientes datos:

• N=5 fuentes
• separación, a=5
• longitud de onda, λ=5

A la derecha, se representa la gráfica de la intensidad medida en la posición x, señalada por una línea de color amarillo, sobre el diagrama de intensidades. Se cambia la posición de dicha línea, en el control titulado Pantalla. Comparamos la gráfica que se obtiene cuando nos situamos cerca de las fuentes, o lejos de las fuentes.