El espejo de Lloyd

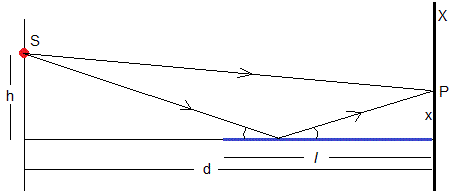
Una fuente S emite ondas de longitud de onda λ. En un punto P de la pantalla situada a una distancia d de la fuente se observa la interferencia de de las ondas que llegan directamente a P y de las que se reflejan en un espejo de longitud l.

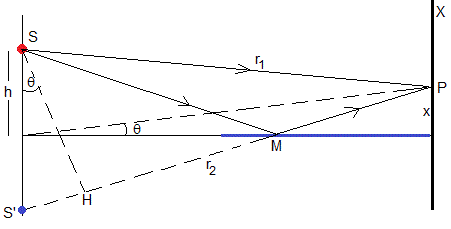
Como vemos en la figura, tenemos en P la interferencia de las ondas producidas por una fuente S y su imagen S', que vibran con la misma frecuencia y en fase

La diferencia de caminos Δ=(SMP)-(SP)=(S'P)-(SP)=r₂-r₁. Como apreciamos en la figura

${\displaystyle \begin{array}{l}\Delta \approx 2h\sin \theta \\ \tan \theta =\frac{x}{d}\approx \sin \theta \\ \Delta \approx 2\frac{h}{d}x\end{array}}$

De otra forma, utilizando la aproximación, $\sqrt{1+x}\approx 1+\frac{x}{2}$

>> syms x;
>> taylor(sqrt(1+x),x)
ans =(7*x^5)/256 - (5*x^4)/128 + x^3/16 - x^2/8 + x/2 + 1

${\displaystyle \begin{array}{l}{r}_1=\sqrt{d^2+{\left(h-x\right)}^2}=d\sqrt{1+\frac{{\left(h-x\right)}^2}{d^2}}\approx d\left(1+\frac{1}{2}\frac{{\left(h-x\right)}^2}{d^2}\right)\\ r_2=\sqrt{d^2+{\left(h+x\right)}^2}=d\sqrt{1+\frac{{\left(h+x\right)}^2}{d^2}}\approx d\left(1+\frac{1}{2}\frac{{\left(h+x\right)}^2}{d^2}\right)\\ \Delta =r_2-r_1\approx \frac{1}{2}\frac{{\left(h+x\right)}^2-{\left(h-x\right)}^2}{d}=2\frac{h}{d}x\end{array}}$

Teniendo en cuenta que el rayos que se refleja en el espejo, experimentan un cambio de fase π, la diferencia de fase, de los dos rayos que llegan a P es

${\displaystyle \delta =k\Delta +\pi =\frac{2\pi }{\lambda }\Delta +\pi =2\pi \left(\frac{2h}{\lambda d}x+\frac{1}{2}\right)}$

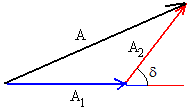
La amplitud resultante en P es

${\displaystyle A=\sqrt{A_1^2+A_2^2+2A_1{A}_2\cos \delta }}$

• La interferencia es constructiva (amplitud máxima) cuando cosδ=1, δ=2nπ

• es destructiva cuando cosδ=-1, δ=(2n+1)π, con n=0, 1,2,3,...

Si la separación d de las fuentes S y S' es pequeña comparada con la distancia d desde las fuentes hasta la pantalla, podemos despreciar la pequeña diferencia entre r₁ y r₂ y suponer que las amplitudes A₁ y A₂ son prácticamente iguales.

${\displaystyle A\approx 2A_1\cos \left(\frac{\delta }{2}\right)}$

La intensidad es proporcional al cuadrado de la amplitud

${\displaystyle I\approx 4I_0{\cos }^2\left(\frac{\delta }{2}\right)=2I_0\left(1+\cos \delta \right)}$

• Interferencia constructiva, I=4I₀, intensidad máxima

La posición del centro de las franjas brillantes es

${\displaystyle \begin{array}{l}\delta =2n\pi \\ 2\pi \left(\frac{2h}{\lambda d}{x}_b+\frac{1}{2}\right)=2n\pi \\ x_b=\left(n-\frac{1}{2}\right)\frac{\lambda d}{2h}\end{array}}$

• Interferencia destructiva, I=0, intensidad mínima

La posición del centro de las franjas oscuras es

${\displaystyle \begin{array}{l}\delta =\left(2n+1\right)\pi \\ 2\pi \left(\frac{2h}{\lambda d}{x}_o+\frac{1}{2}\right)=\left(2n+1\right)\pi \\ x_0=n\frac{\lambda d}{2h}\end{array}}$

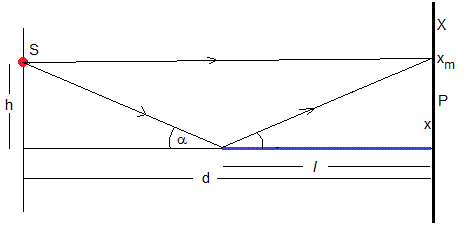
x_m es la distancia máxima a lo largo de la pantalla en la que se produce interferencia

${\displaystyle \begin{array}{l}\tan \alpha =\frac{h}{d-l}\\ x_m=l\tan \alpha =\frac{hl}{d-l}\end{array}}$

Ejemplo

• Distancia entre las fuente y las pantalla, d=80 cm
• Distancia entre la fuente y el espejo, h=1.5 mm
• Longitud del espejo, l=30 cm
• Longitud de onda, λ=0.6·10^-6 m

La posición de la quinta franja brillante, n=5 es x_b=0.72 mm

El número de franjas brillantes que hay en el intervalo es 0<x_b<x_m es

${\displaystyle \left(n-\frac{1}{2}\right)\frac{\lambda d}{2h}<\frac{hl}{d-l}}$

Obtenemos n<6.1250. Es decir, 6 franjas brillantes

Biprisma de Fresnel

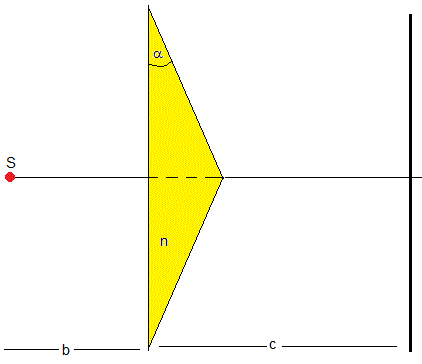
En la figura, se muestra el biprisma de ángulo α hecho con un material transparente de índice de refracción n. Dista b de la fuente de luz S y c de la pantalla

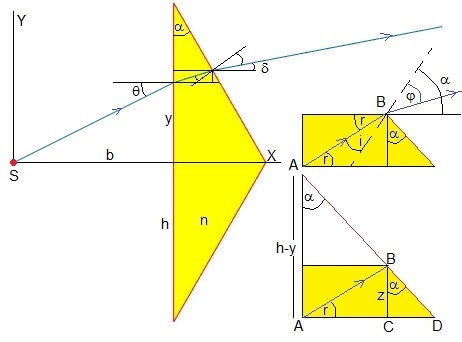
Dibujamos el camino seguido por un rayo que parte de S y llega a la superficie de separación a la altura y del biprisma

Para dibujar parte de la figura, se ha empleado el código

alfa=pi/6; %ángulo del prisma
n=1.5; %índice dee refracción
h=1; %altura del prisma
b=1; %distancia a la fuente
xx=[b, b+h*tan(alfa),b, b];
yy=[h, 0,-h, h];
hold on
fill(xx,yy,'y')
plot(xx,yy,'r')
plot(0,0,'ro','markersize',4,'markeredgecolor','r','markerfacecolor','r')
y=0.5;
th=atan(y/b);
line([0,b],[0,y])
r=asin(sin(th)/n);
z=(h-y)*tan(alfa)*tan(r)/(1+tan(r)*tan(alfa));
line([b,b+(h-y-z)*tan(alfa)],[y,y+z])
phi=asin(n*sin(alfa-r));
line([b+(h-y-z)*tan(alfa), b+(h-y-z)*tan(alfa)+1.5*cos(alfa-phi)],
[y+z, y+z+1.5*sin(alfa-phi)])
hold off
axis equal
axis off

El ángulo de incidencia en la primera superficie es

${\displaystyle \tan \theta =\frac{y}{b}}$

El ángulo de refracción r es más pequeño. Aplicamos la ley de Snell

${\displaystyle \sin \theta =n\sin r}$

El índice de refracción de primer medio, el aire, es n=1

El ángulo de incidencia i en la segunda superficie de separación es

${\displaystyle \begin{array}{l}i+r+90-\alpha =90\\ i=\alpha -r\end{array}}$

El ángulo de refracción φ es más grande

${\displaystyle \begin{array}{l}n\sin i=\sin \phi \\ n\sin \left(\alpha -r\right)=\sin \phi \end{array}}$

El rayo que emerge del prisma forma un ángulo δ=α-φ con la horizontal.

Situamos el origen en la fuente S, el eje X es el eje de simetría. Las coordenadas del punto A son (b, y)

La parte inferior derecha de la figura, nos sugiere las siguientes relaciones

${\displaystyle \begin{array}{l}CD=z\tan \alpha \\ AD=\left(h-y\right)\tan \alpha \\ AC=AD-CD=\left(h-y-z\right)\tan \alpha \\ z=AC\tan r\\ z=\left(h-y-z\right)\tan \alpha \tan r\\ \left(1+\tan \alpha \tan r\right)z=\left(h-y\right)\tan \alpha \tan r\\ z=\frac{\left(h-y\right)\tan \alpha \tan r}{1+\tan \alpha \tan r}\end{array}}$

Las coordenadas del punto B son (b+(h-y-z)tanα, y+z)

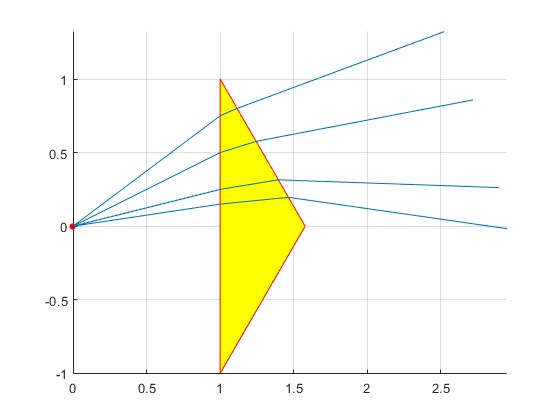
Dibujamos las trayectorias seguidas por los rayos de luz que inciden en en el prisma a las alturas y: 0.15, 0.25, 0.5 y 0.75. Los datos son

• Indice de refracción, n=1.5
• Angulo del prisma, α=π/6 (30°)
• Altura del vértice del biprisma, h=1
• Distancia a la fuente, b=1

alfa=pi/6; %ángulo del prisma
n=1.5; %índice de refracción
h=1; %altura del prisma
b=1; %distancia a la fuente
xx=[b, b+h*tan(alfa),b, b];
yy=[h, 0,-h, h];
hold on
fill(xx,yy,'y')
plot(xx,yy,'r')
plot(0,0,'ro','markersize',4,'markeredgecolor','r','markerfacecolor','r')
for y=[0.15, 0.25, 0.5, 0.75]
    th=atan(y/b);
    line([0,b],[0,y])
    r=asin(sin(th)/n);
    z=(h-y)*tan(alfa)*tan(r)/(1+tan(r)*tan(alfa));
    line([b,b+(h-y-z)*tan(alfa)],[y,y+z])
    phi=asin(n*sin(alfa-r));
    line([b+(h-y-z)*tan(alfa), b+(h-y-z)*tan(alfa)+1.5*cos(alfa-phi)],
[y+z, y+z+1.5*sin(-phi+alfa)])
    line([b+(h-y-z)*tan(alfa), b+(h-y-z)*tan(alfa)+1.5*cos(alfa-phi)],
[y+z, y+z+1.5*sin(alfa-phi)])
end
hold off
grid on
axis equal

Cuando los ángulos de incidencia θ son pequeños

alfa=pi/6; %ángulo del prisma
n=1.5; %índice de refracción
h=1; %altura del prisma
b=1; %distancia a la fuente
xx=[b, b+h*tan(alfa),b, b];
yy=[h, 0,-h, h];
hold on
fill(xx,yy,'y')
plot(xx,yy,'r')
plot(0,0,'ro','markersize',4,'markeredgecolor','r','markerfacecolor','r')
y=b*tan((n-1)*alfa);
th=atan(y/b);
line([0,b],[0,y])
r=asin(sin(th)/n);
z=(h-y)*tan(alfa)*tan(r)/(1+tan(r)*tan(alfa));
line([b,b+(h-y-z)*tan(alfa)],[y,y+z])
phi=asin(n*sin(alfa-r));
line([b+(h-y-z)*tan(alfa), b+(h-y-z)*tan(alfa)+1.5*cos(alfa-phi)],
[y+z, y+z+1.5*sin(alfa-phi)])
line([b+(h-y-z)*tan(alfa), b+(h-y-z)*tan(alfa)+1.5*cos(alfa-phi)],
[y+z, y+z+1.5*sin(alfa-phi)])
line([b+(h-y-z)*tan(alfa), b+(h-y-z)*tan(alfa)-1.5*cos(alfa-phi)],
[y+z, y+z-1.5*sin(alfa-phi)],'lineStyle','--','color','k')
plot(0,(n-1)*b*alfa,'bo','markersize',4,'markeredgecolor','b',
'markerfacecolor','b')
hold off
grid on
axis equal

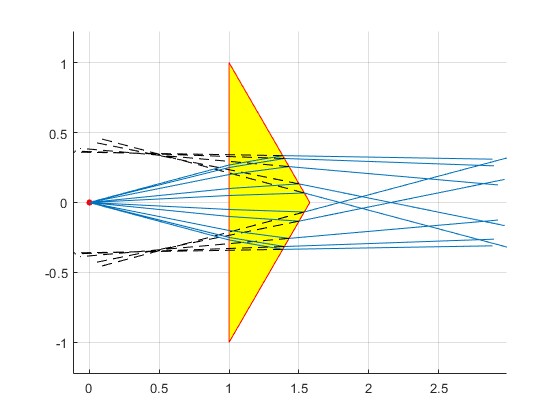
Observamos, que la prolongación de los rayos casi intersecan en dos puntos. Los rayos parecen provenir de dos fuentes virtuales situadas detrás del prisma

Aproximación para ángulos pequeños

Teniendo en cuenta la aproximación

${\displaystyle \sin \theta \approx \tan \theta \approx \theta }$

Ley de Snell de la refracción en A y en B se expresa

${\displaystyle \begin{array}{l}\{\begin{array}{l}\theta \approx n·r\\ n\left(\alpha -r\right)\approx \phi \end{array}\\ \delta =\alpha -\phi =\theta -\left(n-1\right)\alpha \end{array}}$

δ es el ángulo que hace el rayo que emerge del prisma con la horizontal

Para un ángulo θ=(n-1)α, el ángulo δ=0, el rayo refractado por el prisma emerge en la dirección horizontal. La recta está a una altura bθ=b(n-1)α

Cambiamos el ángulo del prisma a otro más pequeño, α=π/12 (15°). Comprobamos que el rayo cuyo ángulo de incidencia es θ=(n-1)α emerge del prisma siguiendo una dirección casi horizontal

alfa=pi/12; %ángulo del prisma
n=1.5; %índice de refracción
h=1; %altura del prisma
b=1; %distancia a la fuente
xx=[b, b+h*tan(alfa),b, b];
yy=[h, 0,-h, h];
hold on
fill(xx,yy,'y')
plot(xx,yy,'r')
plot(0,0,'ro','markersize',4,'markeredgecolor','r','markerfacecolor','r')
y=b*tan((n-1)*alfa);
th=atan(y/b);
line([0,b],[0,y])
r=asin(sin(th)/n);
z=(h-y)*tan(alfa)*tan(r)/(1+tan(r)*tan(alfa));
line([b,b+(h-y-z)*tan(alfa)],[y,y+z])
phi=asin(n*sin(alfa-r));
line([b+(h-y-z)*tan(alfa), b+(h-y-z)*tan(alfa)+1.5*cos(alfa-phi)],
[y+z, y+z+1.5*sin(alfa-phi)])
line([b+(h-y-z)*tan(alfa), b+(h-y-z)*tan(alfa)+1.5*cos(alfa-phi)],
[y+z, y+z+1.5*sin(alfa-phi)])
line([b+(h-y-z)*tan(alfa), b+(h-y-z)*tan(alfa)-1.5*cos(alfa-phi)],
[y+z, y+z-1.5*sin(alfa-phi)],'lineStyle','--','color','k')
plot(0,(n-1)*b*alfa,'bo','markersize',4,'markeredgecolor','b',
'markerfacecolor','b')
hold off
grid on
axis equal

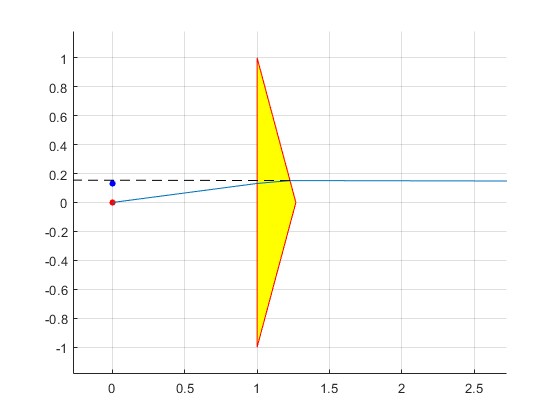
Prolongamos es rayo refractado. La fuente virtual S₁ (en color azul) estará a una altura b(n-1)α por encima de S. Por simetría, la fuente S₂ estará a igual distancia por debajo de S.

El biprisma es equivalente a dos fuentes S₁ y S₂ que vibran con la misma frecuencia y en fase, separadas d=2b(n-1)α, que ya hemos estudiado en la página interferencia

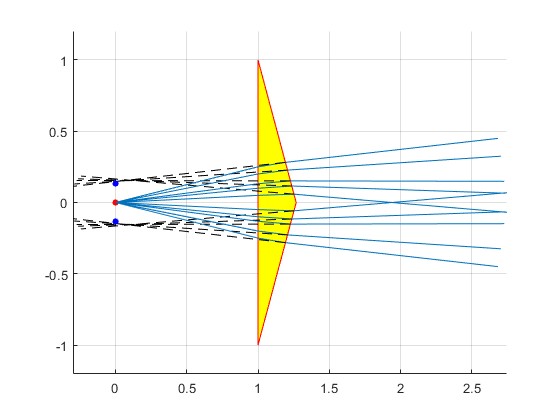
La condición de interferencia constructiva es dsinθ=nλ, donde n es un entero y λ es la longitud de onda

Las posiciones de las franjas brillantes sobre la pantalla situada a una distancia c del briprisma es

${\displaystyle y=\left(b+c\right)\tan \theta \approx \left(b+c\right)\sin \theta =\left(b+c\right)\frac{n\lambda }{d},n=\mathrm{0,}\pm \mathrm{1,}\pm \mathrm{2,.}\pm \mathrm{3,...}}$

La separación entre dos franjas consecutivas es

${\displaystyle \Delta y=\left(b+c\right)\frac{\lambda }{d}=\frac{\left(b+c\right)\lambda }{2\left(n-1\right)b\alpha }}$

Referencias

Michel Henry - Université du Maine. Optique physique : InterférencesMiroir de Lloyd

Pan Pearl River Delta Physics Olympiad 2015, Part-1, problem 4