Interferencia producida por una cuña

Sea una cuña de ángulo α, hecha de un material transparente de índice de refracción n.

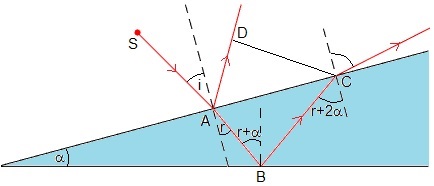
Un rayo parte de la fuente S, formando con la normal a la cuña un ángulo i de incidencia, una parte se refleja en A y la otra parte, se refracta formando un ángulo r con dicha normal. Si el índice de refracción del aire es 1

${\displaystyle \sin i=n\sin r}$

Al llegar a B una parte se refleja hacia el interior de la cuña, formando un ángulo r+α con la normal, y otra parte, se refracta, saliendo de la cuña (no dibujado)

Al llegar a C el rayo reflejado, una parte se refleja hacia el interior (no dibujado) y otra parte, se refracta

${\displaystyle n\sin \left(r+2\alpha \right)=\sin t}$

Para dibujar la cuña y los rayos de ha empleado el código

alfa=pi/12; %plano inclinado
th_i=pi/6; %ángulo de incidencia
n=1.2; %índice de refracción
hold on
line([0,1],[0,0],'color','k')
line([0,1],[0,tan(alfa)],'color','k')
line([0.5,0.5-0.25*sin(alfa)],[0.5*tan(alfa),0.5*tan(alfa)+0.25*cos(alfa)],
'color','k','lineStyle','--')
line([0.5-0.25*sin(th_i+alfa),0.5],[0.5*tan(alfa)+0.25*cos(th_i+alfa),0.5*tan(alfa)],
'color','r') %incidente
plot(0.5-0.25*sin(th_i+alfa),0.5*tan(alfa)+0.25*cos(th_i+alfa),'ro','markersize',4,
'markerfacecolor','r') %fuente
line([0.5,0.5+0.25*sin(th_i-alfa)],[0.5*tan(alfa), 0.5*tan(alfa)+0.25*cos(th_i-alfa)],
'color','r') %reflejado
th=asin(sin(th_i)/n); %refracción
x1=0.5+0.5*tan(alfa)*tan(th+alfa);
line([0.5, x1], [0.5*tan(alfa),0],'color','r')
x2=x1*tan(pi/2-th-alfa)/(tan(pi/2-th-alfa)-tan(alfa));
line([x1, x2],[0,x2*tan(alfa)],'color','r')
th_1=asin(n*sin(th+2*alfa)); %refracción
line([x2,x2+0.25*sin(th_1-alfa)],[x2*tan(alfa), x2*tan(alfa)+0.25*cos(th_1-alfa)],
'color','r')
hold off
axis equal

El ángulo de incidencia i y el ángulo de la cuña α tienen que ser pequeños, de otro modo, se produciría en C la reflexión total hacia el interior de la cuña, es decir, que no haya rayo refractado hacia el exterior de la cuña

Vamos a estudiar la interferencia de los rayos (en la parte superior de la cuña) reflejados en A y los refractados en C. Para ello, hemos de expresar la diferencia de caminos ópticos Δ entre los dos rayos en términos de el índice de refracción n, el ángulo de la cuña, α, el ángulo de incidencia i, el ángulo refractado r y el espesor t de la cuña

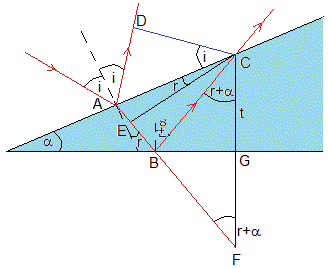
La diferencia de caminos ópticos es Δ=n(AB+BC)-AD=n(AE+EB+BC)-AD

Ahora bien, AD=AC·sini, AE=AC·sinr

Por la ley de Snell de la refracción

${\displaystyle \begin{array}{l}\sin i=n\sin r\\ AD=n·AE\end{array}}$

La diferencia de caminos ópticos es Δ=n(EB+BC)

El triángulo BCF es isósceles, por tanto BC=BF. Por lo que Δ=n(EF)

En el triángulo rectángulo CEF se cumple que EF=CF·cos(r+α)

En el triángulo isósceles BCF, CF=2·CG=2t

La diferencia de caminos ópticos es, Δ=n·2·t·cos(r+α)

Teniendo en cuenta, que el rayo que se refleja en la cuña, experimenta un cambio de fase π, o media longitud de onda. La diferencia de caminos de los dos rayos es, finalmente

${\displaystyle \Delta +\frac{\lambda }{2}=2nt\cos \left(r+\alpha \right)+\frac{\lambda }{2}}$

• Interferencia constructiva

La diferencia de caminos es un múltiplo entero de la longitud de onda

${\displaystyle 2nt\cos \left(r+\alpha \right)+\frac{\lambda }{2}=m\lambda ,m=\mathrm{1,2,3...}}$

• Interferencia destructiva

La diferencia de caminos es un múltiplo semientero de la longitud de onda

${\displaystyle \begin{array}{l}2nt\cos \left(r+\alpha \right)+\frac{\lambda }{2}=\frac{\left(2m+1\right)}{2}\lambda ,m=\mathrm{0,1,2,3...}\\ 2nt\cos \left(r+\alpha \right)=m\lambda \end{array}}$

En el vértice de la cuña, t=0, y m=0, la interferencia es destructiva



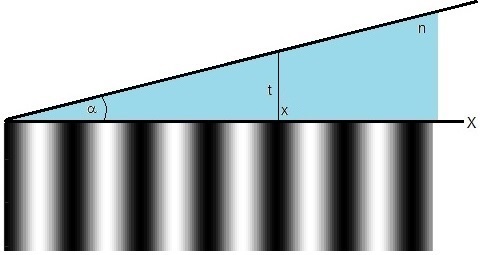
La posición de los mínimos de intensidad (interferencia destructiva) es

${\displaystyle x=\frac{t}{\tan \alpha }=\frac{\frac{m\lambda }{2n\cos \left(r+\alpha \right)}}{\tan \alpha }=\frac{m\lambda }{2n\cos \left(r+\alpha \right)\tan \alpha }}$

Para el caso de incidencia normal i=0, r=0, y para cuñas de pequeño ángulo tanα≈α

${\displaystyle x\approx \frac{m\lambda }{2n\alpha }}$

Intensidad

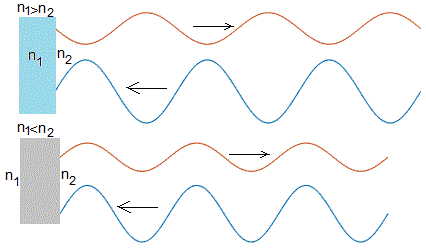
En la página titulada Interferencia de ondas producidas por dos fuentes, calculamos la amplitud resultante de la interferencia de dos rayos

${\displaystyle A=2A_1\cos \left(k\frac{r_2-r_1}{2}\right)}$

r₂-r₁=Δ+λ/2 es la diferencia de caminos (ópticos)

${\displaystyle \begin{array}{l}A=2A_1\cos \left(\frac{2\pi }{\lambda }\frac{\Delta +\frac{\lambda }{2}}{2}\right)=2A_1\cos \left(\frac{2\pi }{\lambda }\frac{2nt\cos \left(r+\alpha \right)+\frac{\lambda }{2}}{2}\right)=\\ A=2A_1\cos \left(\frac{2\pi }{\lambda }nt\cos \left(r+\alpha \right)+\frac{\pi }{2}\right)\end{array}}$

Para incidencia normal, i=r=0

${\displaystyle A\approx 2A_1\cos \left(\frac{2\pi }{\lambda }nt+\frac{\pi }{2}\right)=2A_1\cos \left(\frac{2\pi }{\lambda }n\tan \alpha ·x+\frac{\pi }{2}\right)}$

La intensidad es proporcional al cuadrado de la amplitud

${\displaystyle I=I_0{\cos }^2\left(c·x+\frac{\pi }{2}\right)}$

Utilizamos este código, para representar las franjas brillantes y oscuras

c=10; %coeficiente que multiplica a x
W=2;
s=0.01;
x=0:s:W;
y=0:s:1;
z=cos(c*x+pi/2).^2;
E=repmat(z,length(y),1);
imagesc(x,z,E,[0,1]);colormap(gray);
axis equal

Anillos de Newton

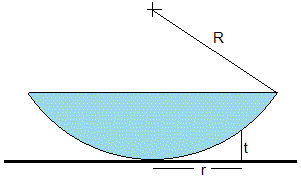
Una lente plano convexa de radio de curvatura grande R se coloca sobre una espejo plano, una cuña de aire se forma entre la superficie curva de la lente y el plano horizontal del espejo.

Si la luz incide normalmente a la superficie horizontal de la lente, se observa anillos concéntricos oscuros y claros. Los anillos de Newton son el resultado de la interferencia, de las ondas de luz provenientes de la parte superior de la cuña de aire, tal como se aprecia en la figura

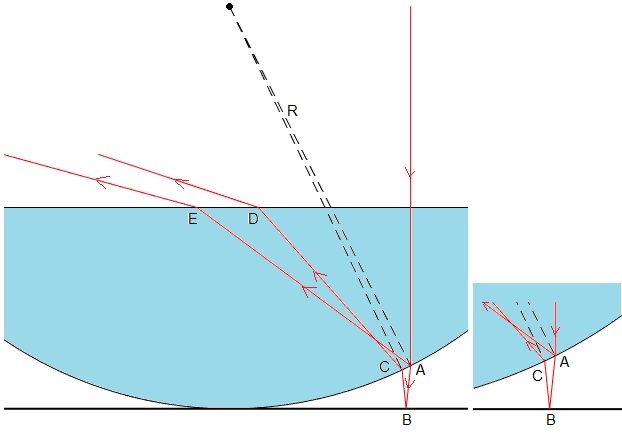
En la figura más abajo, se muestra el camino seguido por un rayo que incide normalmente a la superficie plana de la lente. Al llegar a A en parte se refleja hacia el interior de la lente y en parte, se transmite a la cuña de aire.

Al llegar a B se refleja en el espejo plano. Al volver a la lente en C en parte se refleja (no representado) y en parte, se transmite hacia el interior de la lente

En la parte derecha de la figura, se amplia la trayectoria del rayo transmitido en A a la cuña de aire

El código para dibujar una parte de la figura es

hold on
ang=30;
n=1.2; %índice de refracción
plot(cos((180+ang:360-ang)*pi/180), sin((180+ang:360-ang)*pi/180),'k') 
line([-1,1],[-1,-1],'color','k', 'lineWidth',1.5) 
y1=-sind(ang);
line([-cosd(ang),cosd(ang)],[y1,y1],'color','k')
x1=0.45;
y2=-sqrt(1-x1^2);
line([x1,x1],[0,y2],'color','r') %incidente
line([0,x1],[0,y2],'color','k','lineStyle','--')
r1=asin(x1/sqrt(x1^2+y2^2)); %reflejado en la superficie esférica
x2=x1-(abs(y2)-abs(y1))*tan(2*r1);
line([x1,x2],[y2,y1],'color','r') %reflejado en la superficie esférica
r2=asin(n*sin(2*r1));
line([x2-0.5*sin(r2),x2],[y1+0.5*cos(r2),y1],'color','r')
r3=asin(n*sin(r1));
th=atan(x1/abs(y2)); %ángulo de la normal
x3=x1-(1-abs(y2))*tan(r3-th);
line([x1,x3],[y2,-1],'color','r')
m=tan(pi/2+r3-th);
b=-1-m*x3;
x4=(-m*b+sqrt(m^2*b^2-(1+m^2)*(b^2-1)))/(1+m^2);
y4=-sqrt(1-x4^2);
line([x4,x3],[y4,-1],'color','r') %reflejado en el espejo
th_1=atan(x4/abs(y4)); %ángulo de la normal
r4=asin(sin(th_1-r3+th)/n);
x5=x4-(abs(y4-y1))*tan(th_1+r4);
line([0,x4],[0,y4],'color','k','lineStyle','--')
line([x4,x5],[y4,y1],'color','r')
r5=asin(n*sin(th_1+r4));
line([x5-0.5*sin(r5),x5],[y1+0.5*cos(r2),y1],'color','r')

hold off
axis equal

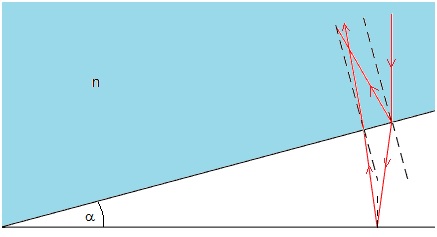
Aproximamos la cuña de aire formada por una superficie esférica y una superficie plana por una cuña formada por dos superficies planas formando un pequeño ángulo α

alfa=pi/12; %plano inclinado
n=1.5; %índice de refracción
hold on
x1=0.9;
y1=x1*tan(alfa);
line([0,1],[0,0],'color','k')
line([0,1],[0,tan(alfa)],'color','k')
line([x1,x1-0.25*sin(alfa)],[y1,y1+0.25*cos(alfa)],'color','k','lineStyle','--')
line([x1,x1],[y1,y1+0.25],'color','r')
r1=asin(n*sin(alfa));
line([x1,x1-0.25*sin(2*alfa)],[y1,y1+0.25*cos(2*alfa)],'color','r')
x2=x1-y1*tan(r1-alfa);
line([x2,x1],[0,y1],'color','r')
m=tan(pi/2+r1-alfa);
x3=m*x2/(m-tan(alfa));
y3=x3*tan(alfa);
line([x2,x3],[0,y3],'color','r')
r2=asin(sin(r1-2*alfa)/n);
line([x3,x3-0.25*sin(alfa)],[y3,y3+0.25*cos(alfa)],'color','k','lineStyle','--')
line([x3,x3-0.25*sin(r2+alfa)],[y3,y3+0.25*cos(r2+alfa)],'color','r')
hold off
axis equal

Diferencia de caminos ópticos

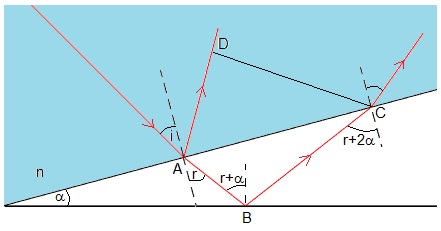
El rayo incidente forma con la normal a la cuña de aire un ángulo i, una parte se refleja en A y la otra parte, se refracta formando un ángulo r con dicha normal. Si el índice de refracción del aire es 1 y el de la lente n

${\displaystyle n\sin i=\sin r}$

Al llegar a B una parte se refleja hacia el interior de la cuña, formando un ángulo r+α con la normal, y otra parte, se refracta, saliendo de la cuña (no dibujado)

Al llegar a C el rayo reflejado, una parte se refleja hacia el interior (no dibujado) y otra parte, se refracta

${\displaystyle \sin \left(r+2\alpha \right)=n\sin t}$

Para dibujar la cuña de aire y los rayos de ha empleado el código

alfa=pi/12; %plano inclinado
th_i=pi/6; %ángulo de incidencia
n=1.2; %índice de refracción
hold on
line([0,1],[0,0],'color','k')
line([0,1],[0,tan(alfa)],'color','k')
line([0.5,0.5-0.25*sin(alfa)],[0.5*tan(alfa),0.5*tan(alfa)+0.25*cos(alfa)],'color',
'k','lineStyle','--')
line([0.5-0.25*sin(th_i+alfa),0.5],[0.5*tan(alfa)+0.25*cos(th_i+alfa),0.5*tan(alfa)],
'color','r') %incidente
plot(0.5-0.25*sin(th_i+alfa),0.5*tan(alfa)+0.25*cos(th_i+alfa),'ro','markersize',4,
'markerfacecolor','r') %fuente
line([0.5,0.5+0.25*sin(th_i-alfa)],[0.5*tan(alfa), 0.5*tan(alfa)+0.25*cos(th_i-alfa)],
'color','r') %reflejado
th=asin(sin(th_i)/n); %refracción
x1=0.5+0.5*tan(alfa)*tan(th+alfa);
line([0.5, x1], [0.5*tan(alfa),0],'color','r')
x2=x1*tan(pi/2-th-alfa)/(tan(pi/2-th-alfa)-tan(alfa));
line([x1, x2],[0,x2*tan(alfa)],'color','r')
th_1=asin(n*sin(th+2*alfa)); %refracción
line([x2,x2+0.25*sin(th_1-alfa)],[x2*tan(alfa), x2*tan(alfa)+0.25*cos(th_1-alfa)],
'color','r')
hold off
axis equal

En el apartado anterior, hemos calculado la diferencia de caminos ópticos entre el rayo reflejado AD y el refractado ABC

La diferencia de caminos ópticos es Δ=(AB+BC)-nAD=(AE+EB+BC)-n(AD)

Ahora bien, AD=AC·sini, AE=AC·sinr (véase la segunda figura)

Por la ley de Snell de la refracción

${\displaystyle \begin{array}{l}n\sin i=\sin r\\ n·AD=AE\end{array}}$

La diferencia de caminos ópticos es Δ=(EB+BC)

El triángulo BCF es isósceles (véase la segunda figura), por tanto BC=BF. Por lo que Δ=(EF)=2tcos(r+α), tal como demostramos en el apartado anterior

Si los rayos inciden normalmente a la superficie plana de la lente, i=0, r=0. Si el radio de la lente R es grande, α es un ángulo que aumenta a medida que nos alejamos del punto de contacto, pero sigue siendo muy pequeño

Δ≈2t

Teniendo en cuenta que el rayo que se refleja en B en el espejo, experimenta un cambio de fase π, o media longitud de onda. La diferencia de caminos ópticos, de los dos rayos es

${\displaystyle 2t+\frac{\lambda }{2}}$

• Interferencia constructiva

La diferencia de caminos es un múltiplo entero de la longitud de onda

${\displaystyle \begin{array}{l}2t+\frac{\lambda }{2}=m\lambda ,m=\mathrm{1,2,3...}\\ 2t=\frac{2m-1}{2}\lambda \end{array}}$

• Interferencia destructiva

La diferencia de caminos es un múltiplo semientero de la longitud de onda

${\displaystyle \begin{array}{l}2t+\frac{\lambda }{2}=\frac{2m+1}{2}\lambda ,m=\mathrm{0,1,2,3...}\\ 2t=m\lambda \end{array}}$

Par t=0, m=0, el origen situado en el punto de contacto hay interferencia destructiva

Radios de los anillos

${\displaystyle \{\begin{array}{l}r=R\sin \theta \\ t=R-R\cos \theta \end{array}}$

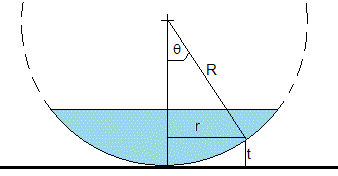
Eliminando el ángulo θ, de este sistema de dos ecuaciones

${\displaystyle \begin{array}{l}t=R-\sqrt{R^2-r^{{}^2}}\\ r^2=2Rt-t^2\end{array}}$

Como t es muy pequeño frente a R

${\displaystyle r^2\approx 2Rt}$

• Interferencia constructiva. Radio de los anillos brillantes

${\displaystyle \frac{r_m^2}{R}=\frac{2m-1}{2}\lambda }$

• Interferencia destructiva. Radio de los anillos oscuros

${\displaystyle \frac{r_m^2}{R}=m\lambda }$

Intensidad

En la página titulada Interferencia de ondas producidas por dos fuentes, calculamos la amplitud resultante de la interferencia de dos rayos

${\displaystyle A=2A_1\cos \left(k\frac{r_2-r_1}{2}\right)}$

r₂-r₁=2t+λ/2 es la diferencia de caminos (ópticos)

${\displaystyle \begin{array}{l}A=2A_1\cos \left(k\frac{r_2-r_1}{2}\right)=2A_1\cos \left(\frac{2\pi }{\lambda }\frac{2t+\frac{\lambda }{2}}{2}\right)=2A_1\cos \left(\frac{2\pi }{\lambda }t+\frac{\pi }{2}\right)\\ A\approx 2A_1\cos \left(\frac{2\pi }{\lambda }\frac{r^2}{2R}+\frac{\pi }{2}\right)=2A_1\cos \left(\pi \frac{r^2}{\lambda R}+\frac{\pi }{2}\right)\end{array}}$

La intensidad es proporcional al cuadrado de la amplitud

${\displaystyle I=I_0{\cos }^2\left(\pi \frac{r^2}{\lambda R}+\frac{\pi }{2}\right)}$

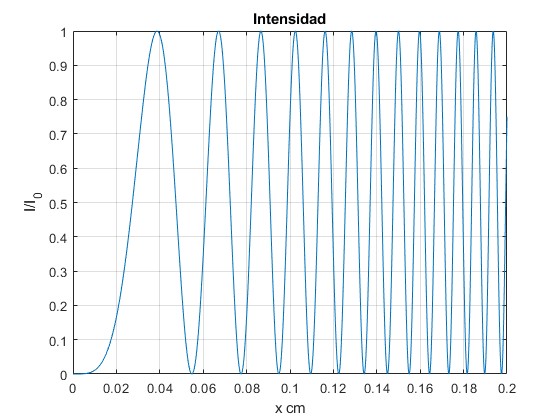
Sea una lente de radio R=60 cm, representamos la intensidad debida a la interferencia de luz de longitud de onda, λ=0.00005 cm

R=60; %radio en cm
lambda=0.00005; %longitud de onda en cm
f=@(x) cos(pi*x.^2/(lambda*R)+pi/2).^2;
fplot(f,[0,0.2])
grid on
xlabel('x cm')
ylabel('I/I_0')
title('Intensidad')

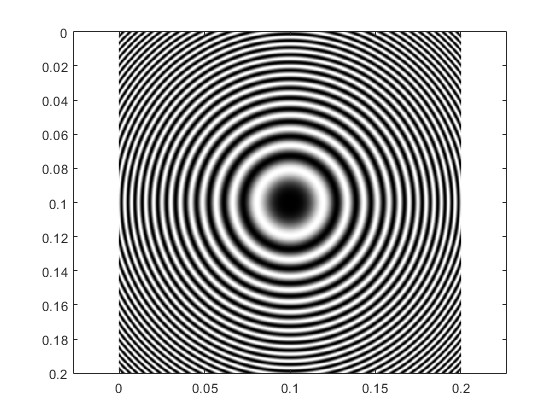
Representamos los anillos de Newton, con estos datos

R=60; %radio en cm
lambda=0.00005; %longitud de onda en cm
f=@(r2) cos(pi*r2/(lambda*R)+pi/2).^2;

X=0:0.001:0.2;
Y=0:0.001:0.2;
M=zeros(length(X), length(Y));
for i=1:length(X)
    for j=1:length(Y)
        r2=X(i)^2+Y(j)^2;
        M(i,j)=f(r2);
    end
end

M=flipud(M); %primer cuadrante
[m,n]=size(M);
E=zeros(m,2*n-1);
E(1:m,n:2*n-1)=M;
E(1:m,1:n-1)=fliplr(M(1:m,2:n));
F=flipud(E(1:m-1,:));
H=[E;F];

imagesc(X,Y,H,[0,1]);colormap(gray);
axis equal

Cambiamos la longitud de onda a λ=0.00015 cm

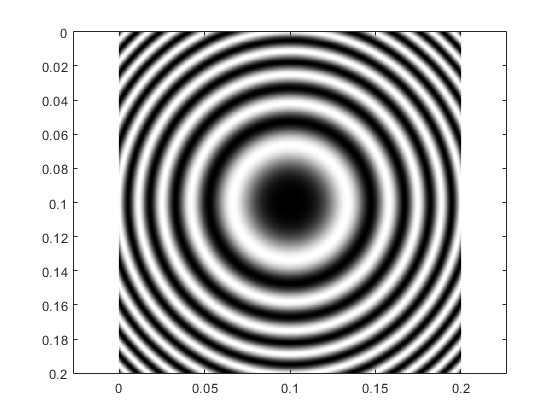
El código que realiza los cálculos en el primer cuadrante y representa la intensidad, siguiendo los pasos explicados en la página titulada Gráficos tridimensionales en el apartado titulado Simetría

Referencias

Madan Mohan Malaviya. Interference. UNIT III, Optics, Lecture-3. Univ. of Technology, Gorakhpur