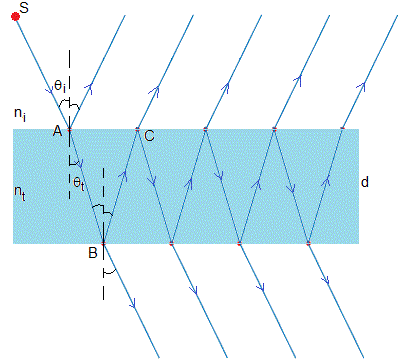
Sea un medio (película) trasparente de anchura d e índice de refracción n_t (color azul claro) rodeado de otro medio (aire, agua) de índice de refracción n_i. Un rayo de luz procedente de la fuente S incide en A sobre la película formando un ángulo θ_i con la normal. El rayo de luz en parte, se refleja formando un ángulo θ_i y otra parte, se refracta formando un ángulo θ_t con la normal

${\displaystyle n_i\sin {\theta }_i=n_t\sin {\theta }_t}$

El rayo refractado llega a la superficie inferior de la película en B y en parte, se refleja hacia en interior formando un ángulo θ_t y otra parte, se refracta (se transmite) formando un ángulo θ_i con la normal

El rayo refejeado hacia en interior que parte de B llega al la superficie superior de la película en C, en parte se refeja hacia el interior formando un θ_t y otra parte, se refracta (transmite) formando un ángulo θ_i con la normal. Y así, sucesivamente

Caminos ópticos

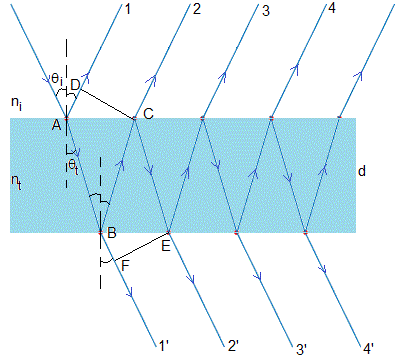
El rayo (2) que parte de A viaja por la película, se refleja en B y llega a C. La parte transmitida hacia el exterior, interfiere con el rayo (1) reflejado en A. La diferencia de caminos ópticos entre los dos rayos es

${\displaystyle \begin{array}{l}\Delta =n_t\left(AB+BC\right)-n_{i}AD\\ =n_{t}2\frac{d}{\cos {\theta }_t}-n_i·2d\tan {\theta }_t\sin {\theta }_i=2\frac{d}{\cos {\theta }_t}{n}_t\left(1-{\sin }^2{\theta }_t\right)=2d{n}_t\cos {\theta }_t\end{array}}$

La diferencia de caminos ópticos es la misma para los rayos (2) y (3), (3) y (4) y así, sucesivamente

La diferencia de fase δ=kΔ=2πΔ/λ. Siendo λ la longitud de onda

En la parte inferior de la figura, la diferencia de caminos ópticos entre los rayos (1') refractado en B y (2') reflejado en B y C y refractado en E es el mismo

${\displaystyle \Delta =n_t\left(BC+CE\right)-n_{i}BF=2d{n}_t\cos {\theta }_t}$

Relaciones de Stokes

Denominamos

• Coeficente de reflexión r=E_r/E_i cuando la reflexíón se produce en el primer medio de índice de refracción n_i
• Coeficente de transmisión t=E_t/E_i cuando la refracción se produce del primer medio al segundo
• Coeficente de reflexión r'=E'_r/E'_i cuando la reflexíón se produce en el segundo medio de índice de refracción n_t
• Coeficente de transmisión t'=E'_t/E'_i cuando la refracción se produce del segundo medio al primero

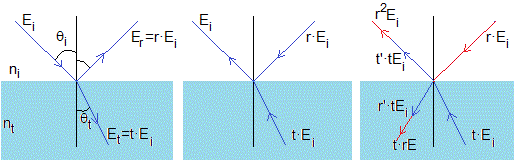
Existe una relación entre los coeficientes r y r' y entre t y t' denominadas relaciones de Stokes

• En la parte izquierda de la figura, se representa el fenómeno de la refexión y refracción de un rayo de luz al pasar de un medio a otro de distinto índice de refracción

• En la parte central, la inversión temporal

• En la parte derecha.

• El rayo de color rojo, de amplitud r·E_i incide en la superficie de separación y produce un rayo refejado de amplitud r·(r·E_i)=r²E_i y uno transmitido de amplitud t·(r·E_i)

• El rayo de color azul, de amplitud t·E_i incide en la superficie de separación y produce un rayo refejado de amplitud r'·(t·E_i) y uno transmitido de amplitud t'·(t·E_i)

Comparamos la parte izquerda y derecha de la figura, estableciendo las siguientes relaciones

${\displaystyle \begin{array}{l}\{\begin{array}{l}{r}^2{E}_i+t\text{'}·t{E}_i=E_i\\ r\text{'}·t{E}_i+t·r{E}_i=0\end{array}\\ \{\begin{array}{l}t\text{'}t=1-r^2\\ r\text{'}=-r\end{array}\end{array}}$

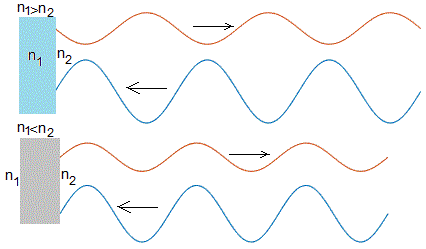
Cuando una onda luminosa se refleja cambia de fase π (180°) si el índice de refracción n₁>n₂. Véase la animación de la página titulada Solución d'Alembert de la ecuación de onda, en el apartado titulado Cuerda semi-infinita

Amplitudes

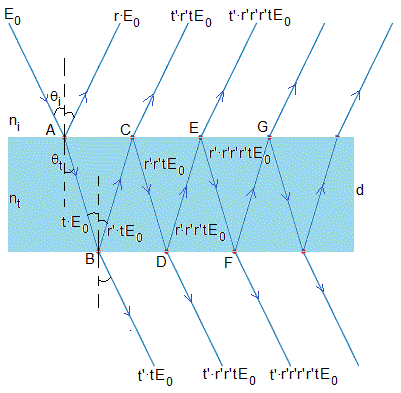
El rayo incidente tiene una amplitud E₀

• en A, se refleja rE₀ y se refracta tE₀
• en B, se refleja r'(tE₀) y se refracta t'(tE₀)
• en C, el rayo reflejado en B (r'tE₀) llega a C, se refleja r'(r'tE₀) y se refracta t'(r'tE₀)
• en D, el rayo reflejado en C (r'r'tE₀) llega a D, se refleja r'(r'r'tE₀) y se refracta t'(r'r'tE₀)
• y así, sucesivamente.

Interferencia de los rayos reflejados (parte superior)

• La amplitud E_R de la interferencia de los rayos (1), (2) , (3)... (parte superior). Véase la página titulada Interferencia de ondas producidas por varias fuentes, la forma de calcular la amplitud resultante empleando números complejos

${\displaystyle \begin{array}{l}{E}_1=\left(r{E}_0\right)\\ E_2=\left(tt\text{'}r\text{'}{E}_0\right)e^{-i\delta }\\ E_3=\left(tt\text{'}r{\text{'}}^3{E}_0\right)e^{-i2\delta }\\ E_4=\left(tt\text{'}r{\text{'}}^5{E}_0\right)e^{-i3\delta }\\ \mathrm{....}\\ E_k=\left(tt\text{'}r{\text{'}}^{2k-3}{E}_0\right)e^{-i(k-1)\delta }\\ E_R=E_0\left(r+tt\text{'}r\text{'}{e}^{-i\delta }{\displaystyle \sum _{k=1}^{\infty }r{\text{'}}^{2k-4}{e}^{-i(k-2)\delta }}\right)\end{array}}$

La suma de los infinitos términos de una progresión geométrica es

${\displaystyle \begin{array}{l}{S}_{\infty }=\frac{a_0}{1-r}\\ E_R=E_0\left(r+tt\text{'}r\text{'}{e}^{-i\delta }\frac{1}{1-r{\text{'}}^2{e}^{-i\delta }}\right)\end{array}}$

Utilizando las relaciones de Stokes

${\displaystyle \begin{array}{l}\{\begin{array}{l}r\text{'}=-r\\ t\text{'}t=1-r^2\end{array}\\ E_R=E_0\left(r-\frac{r\left(1-r^2\right)e^{-i\delta }}{1-r^2{e}^{-i\delta }}\right)=E_0\left(\frac{r\left(1-e^{-i\delta }\right)}{1-r^2{e}^{-i\delta }}\right)\end{array}}$

• La amplitud E_T de la interferencia de los rayos (1'), (2') , (3')... (parte inferior)

${\displaystyle \begin{array}{l}{E}_1=t\text{'}t{E}_0\\ E_2=\left(tt\text{'}r{\text{'}}^2{E}_0\right)e^{-i\delta }\\ E_3=\left(tt\text{'}r{\text{'}}^4{E}_0\right)e^{-i2\delta }\\ E_4=\left(tt\text{'}r{\text{'}}^6{E}_0\right)e^{-i3\delta }\\ \mathrm{....}\\ E_k=\left(tt\text{'}r{\text{'}}^{2k-2}{E}_0\right)e^{-i(k-1)\delta }\\ E_T=tt\text{'}{E}_0\left({\displaystyle \sum _{k=1}^{\infty }r{\text{'}}^{2k-2}{e}^{-i(k-1)\delta }}\right)\end{array}}$

La suma de los infinitos términos de una progresión geométrica es

${\displaystyle E_T=E_{0}tt\text{'}\left(\frac{1}{1-r{\text{'}}^2{e}^{-i\delta }}\right)}$

Utilizando las relaciones de Stokes

${\displaystyle E_T=E_0\frac{1-r^2}{1-r^2{e}^{-i\delta }}}$

Intensidad

La intensidad es proporcional al cuadrado de la amplitud

${\displaystyle \begin{array}{l}{I}_R={\left|E_R\right|}^2=E_0^2\left(\frac{r\left(1-e^{-i\delta }\right)}{1-r^2{e}^{-i\delta }}\right)\left(\frac{r\left(1-e^{i\delta }\right)}{1-r^2{e}^{i\delta }}\right)=E_0^2\frac{2r^2\left(1-\cos \delta \right)}{1+r^4-2r^2\cos \delta }=\\ E_0^2\frac{2r^2·2{\sin }^2\left(\frac{\delta }{2}\right)}{1+r^4-2r^2+2r^2-2r^2\cos \delta }=E_0^2\frac{4r^2{\sin }^2\left(\frac{\delta }{2}\right)}{{\left(1-r^2\right)}^2+4r^2{\sin }^2\left(\frac{\delta }{2}\right)}\end{array}}$

Expresamos de otra forma equivalente la intensidad, definiendo el número F

${\displaystyle I_R=E_0^2\frac{F{\sin }^2\left(\frac{\delta }{2}\right)}{1+F{\sin }^2\left(\frac{\delta }{2}\right)},F=\frac{4r^2}{{\left(1-r^2\right)}^2}}$

Del mismo modo, calculamos I_T

${\displaystyle \begin{array}{l}{I}_T=\left(E_0\frac{1-r^2}{1-r^2{e}^{-i\delta }}\right)\left(E_0\frac{1-r^2}{1-r^2{e}^{+i\delta }}\right)=E_0^2\frac{{\left(1-r^2\right)}^2}{1+r^4-2r^2\cos \delta }=\\ E_0^2\frac{{\left(1-r^2\right)}^2}{{\left(1-r^2\right)}^2+4r^2{\sin }^2\left(\frac{\delta }{2}\right)}=E_0^2\frac{1}{1+F{\sin }^2\left(\frac{\delta }{2}\right)}\end{array}}$

Comprobamos que

${\displaystyle I_R+I_T=E_0^2}$

la intensidad de la luz incidente

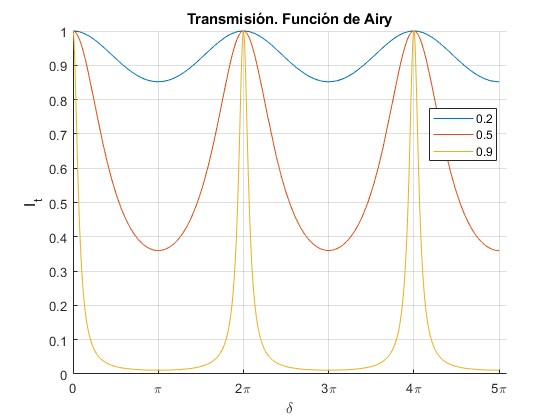
Representamos el coeficiente de transmisión $T=\frac{I_T}{E_0^2}$ para tres valores de r=0.2, 0.5 y 0.9 (o del número F) en función del ángulo de fase δ en radianes

hold on
for r=[0.2,0.5,0.9]
    F=4*r^2/(1-r^2)^2;
    f=@(x) 1./(1+F*sin(x/2).^2);
    fplot(f,[0,5*pi],'displayName',num2str(r))
end
hold off
set(gca,'XTick',0:pi:5*pi)
set(gca,'XTickLabel',{'0','\pi','2\pi','3\pi','4\pi','5\pi'})
grid on
legend('-DynamicLegend','location','best')
xlabel('\delta')
ylabel('I_t')
title('Transmisión. Función de Airy')

Resumen

Todos los rayos reflejados (2), (3), (4), ..., excepto el primero (1), están, en fase. El primero (1) y el segundo (2) están en oposición de fase.

El mínimo de la intensidad I_R=0 ocurre cuando cosδ=1. El primer rayo (1) reflejado interfiere destructivamente con todos los demás rayos reflejados, (2), (3), (4)...

La diferencia de caminos ópticos Δ es un múltiplo entero de la longitud de onda λ

${\displaystyle \begin{array}{l}\delta =2\pi m,m=\mathrm{0,1,2...}\\ \Delta =2d{n}_t\cos {\theta }_t=m\lambda \end{array}}$

El máximo de I_R ocurre cuando cosδ=-1, δ=π, 3π, 5π, ...

${\displaystyle \begin{array}{l}\delta =2\pi \left(m+\frac{1}{2}\right),m=\mathrm{0,1,2...}\\ \Delta =2d{n}_t\cos {\theta }_t=\left(m+\frac{1}{2}\right)\lambda \end{array}}$

Esta es la condición para que I_T sea mínimo

${\displaystyle I_R=E_0^2\frac{4r^2}{1+r^4+2r^2}=E_0^2{\left(\frac{2r}{1+r^2}\right)}^2}$

Ecuaciones de Fresnel

Las ecuaciones de Fresnel nos proporcionan los coeficientes r y t para las ondas electromagnéticas polarizadas que se propagan del medio de índice de refracción n_i al medio de índice de refracción n_t

${\displaystyle \begin{array}{l}{t}_{\perp }={\left(\frac{E_{0t}}{E_{0i}}\right)}_{\perp }=\frac{2n_i\cos {\theta }_i}{n_i\cos {\theta }_i+n_t\cos {\theta }_t},r_{\perp }={\left(\frac{E_{0r}}{E_{0i}}\right)}_{\perp }=\frac{n_i\cos {\theta }_i-n_t\cos {\theta }_t}{n_i\cos {\theta }_i+n_t\cos {\theta }_t}\\ t_{\parallel }={\left(\frac{E_{0t}}{E_{0i}}\right)}_{\parallel }=\frac{2n_i\cos {\theta }_i}{n_t\cos {\theta }_i+n_i\cos {\theta }_t},r_{\parallel }={\left(\frac{E_{0r}}{E_{0i}}\right)}_{\parallel }=\frac{-n_t\cos {\theta }_i+n_i\cos {\theta }_t}{n_t\cos {\theta }_i+n_i\cos {\theta }_t}\end{array}}$

La ley de Snell relaciona el ángulo de incidencia θ_i y el de refracción θ_t

${\displaystyle n_i\sin {\theta }_i=n_t\sin {\theta }_t}$

• Polarización ⊥. El campo eléctrico es normal al plano de incidencia

${\displaystyle \begin{array}{l}{F}_{\perp }=\frac{4r_{\perp }^2}{{\left(1-r_{\perp }^2\right)}^2}\\ 1-r_{\perp }^2=1-{\left(\frac{n_i\cos {\theta }_i-n_t\cos {\theta }_t}{n_i\cos {\theta }_i+n_t\cos {\theta }_t}\right)}^2=\frac{4n_i\cos {\theta }_i·n_t\cos {\theta }_t}{{\left(n_i\cos {\theta }_i+n_t\cos {\theta }_t\right)}^2}\\ F_{\perp }=\frac{4{\left(\frac{n_i\cos {\theta }_i-n_t\cos {\theta }_t}{n_i\cos {\theta }_i+n_t\cos {\theta }_t}\right)}^2}{{\left(\frac{4n_i\cos {\theta }_i·n_t\cos {\theta }_t}{{\left(n_i\cos {\theta }_i+n_t\cos {\theta }_t\right)}^2}\right)}^2}=\frac{{\left(n_i\cos {\theta }_i-n_t\cos {\theta }_t\right)}^2{\left(n_i\cos {\theta }_i+n_t\cos {\theta }_t\right)}^2}{4{\left(n_i\cos {\theta }_i·n_t\cos {\theta }_t\right)}^2}=\\ =\frac{{\left(n_i^2{\cos }^2{\theta }_i-n_t^2{\cos }^2{\theta }_t\right)}^2}{4n_i^2{n}_t^2{\cos }^2{\theta }_i{\cos }^2{\theta }_t}=\frac{{\left(n_i^2{\cos }^2{\theta }_i-n_t^2\left(1-{\sin }^2{\theta }_t\right)\right)}^2}{4n_i^2{n}_t^2{\cos }^2{\theta }_i\left(1-{\sin }^2{\theta }_t\right)}=\frac{{\left(n_i^2-n_t^2\right)}^2}{4n_i^2{\cos }^2{\theta }_i\left(n_t^2-n_i^2{\sin }^2{\theta }_i\right)}\end{array}}$

El coeficiente de transmisión es

${\displaystyle T_{\perp }=\frac{1}{1+F_{\perp }{\sin }^2\left(\frac{\delta }{2}\right)}}$

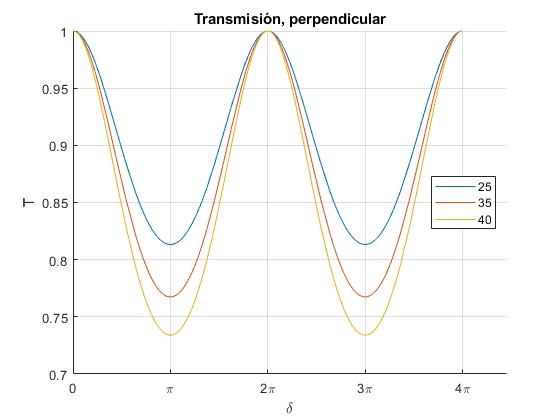
Una placa de vidrio n_t=1.5 está rodeada por aire n_i=1. Representamos el coeficiente de transmisión T_⊥ en función del la diferencia de fase δ para tres ángulos de incidencia θ_i=25°, 30° y 35°

ni=1; %índice de refracción del aire
nt=1.5; % del vidrio
hold on
for th=[25,35,40]*pi/180 %ángulo de incidencia
    F=(ni^2-nt^2)^2/(4*ni^2*cos(th)^2*(nt^2-ni^2*sin(th)^2));
    f=@(x) 1./(1+F*sin(x/2).^2);
    fplot(f,[0,4*pi],'displayName',num2str(th*180/pi))
end
hold off
set(gca,'XTick',0:pi:5*pi)
set(gca,'XTickLabel',{'0','\pi','2\pi','3\pi','4\pi','5\pi'})
grid on
legend('-DynamicLegend','location','best')
xlabel('\delta')
ylabel('T')
title('Transmisión, perpendicular')



• Polarización ||. El campo eléctrico es paralelo al plano de incidencia

${\displaystyle \begin{array}{l}{F}_{\parallel }=\frac{4r_{\parallel }^2}{{\left(1-r_{\parallel }^2\right)}^2}\\ 1-r_{\parallel }^2=1-{\left(\frac{-n_t\cos {\theta }_i+n_i\cos {\theta }_t}{n_t\cos {\theta }_i+n_i\cos {\theta }_t}\right)}^2=\frac{4n_i{n}_t\cos {\theta }_i\cos {\theta }_t}{{\left(n_t\cos {\theta }_i+n_i\cos {\theta }_t\right)}^2}\\ F_{\parallel }=\frac{4{\left(-n_t\cos {\theta }_i+n_i\cos {\theta }_t\right)}^2{\left(n_t\cos {\theta }_i+n_i\cos {\theta }_t\right)}^2}{{\left(4n_i{n}_t\cos {\theta }_i\cos {\theta }_t\right)}^2}=\frac{{\left(n_i^2{\cos }^2{\theta }_t-n_t^2{\cos }^2{\theta }_i\right)}^2}{4n_i^2{\cos }^2{\theta }_i\left(n_t^2-n_i^2{\sin }^2{\theta }_i\right)}=\\ \frac{{\left(n_i^2\left(1-\frac{n_i^2}{n_t^2}{\sin }^2{\theta }_i\right)-n_t^2\left(1-{\sin }^2{\theta }_i\right)\right)}^2}{4n_i^2{\cos }^2{\theta }_i\left(n_t^2-n_i^2{\sin }^2{\theta }_i\right)}=\frac{{\left(n_i^2-n_t^2+\left(n_t^2-\frac{n_i^4}{n_t^2}\right){\sin }^2{\theta }_i\right)}^2}{4n_i^2{\cos }^2{\theta }_i\left(n_t^2-n_i^2{\sin }^2{\theta }_i\right)}\end{array}}$

El coeficiente de transmisión es

${\displaystyle T_{\parallel }=\frac{1}{1+F_{\parallel }{\sin }^2\left(\frac{\delta }{2}\right)}}$

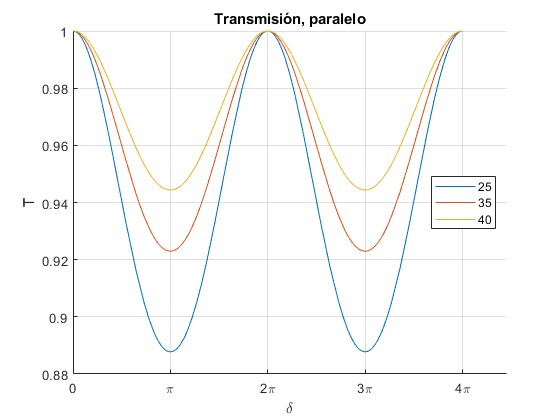
Representamos el coeficiente de transmisión T_|| en función del la diferencia de fase δ para tres ángulos de incidencia θ_i=25°, 30° y 35°

ni=1; %índice de refracción del aire
nt=1.5; % del vidrio
hold on
for th=[25,35,40]*pi/180 %ángulo de incidencia
    F=(ni^2-nt^2+(nt^2-ni^4/nt^2)*sin(th)^2)^2/(4*ni^2*cos(th)^2*
(nt^2-ni^2*sin(th)^2));
    f=@(x) 1./(1+F*sin(x/2).^2);
    disp(F)
    fplot(f,[0,4*pi],'displayName',num2str(th*180/pi))
end
hold off
set(gca,'XTick',0:pi:5*pi)
set(gca,'XTickLabel',{'0','\pi','2\pi','3\pi','4\pi','5\pi'})
grid on
legend('-DynamicLegend','location','best')
xlabel('\delta')
ylabel('T')
title('Transmisión, paralelo')

Referencias

Nelly Schulz. Stokes Relations