El oscilador de Fermi
Introducción al régimen caótico
Consideremos el siguiente sistema oscilante: una partícula de masa m, se deja caer desde una altura h, sobre una plataforma de masa M unida a un muelle elástico de constante k. La partícula cae y choca elásticamente con la plataforma, el bloque asciende y desciende, la plataforma oscila y se vuelven a encontrar al cabo de un cierto tiempo, chocan y así, sucesivamente.
Se aplica la segunda ley de Newton para estudiar el movimiento del sistema formado por el muelle y la plataforma, las ecuaciones del movimiento de caída libre para estudiar el movimiento del bloque. En el momento del choque, se aplica el principio de conservación del momento lineal y de la energía.
El sistema es conservativo, la energía del sistema formado por el bloque, el muelle y la plataforma se mantiene constante.
Ecuaciones del movimiento
Estudiamos las distintas etapas del movimiento del bloque y de la plataforma, para ello establecemos el origen en la posición del extremo del muelle sin deformar. Vamos a disponer de dos relojes uno que mide el tiempo parcial t de cada una de las etapas del movimiento y otro que mide el tiempo total tt, desde el momento en el que se libera el bloque a una altura h sobre el origen.
Situación inicial
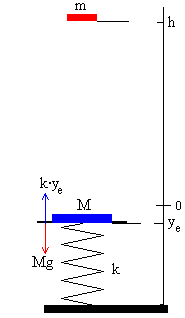
En la figura, se muestra la situación inicial. El bloque de masa m está a una altura h sobre el origen. La plataforma de masa M descansa sobre el muelle elástico de constante k. La plataforma desciende una altura ye, hasta que se equilibran el peso Mg y la fuerza que ejerce el muelle k·ye.
ye=Mg/k
La energía inicial del sistema formado por el bloque, el muelle y la plataforma es
Movimiento del bloque
Se libera el bloque, las ecuaciones del movimiento son:
El bloque permanece en reposo, en la posición de equilibrio, tal como se muestra en la figura
y=-ye
vy=0
El choque ente el bloque y la plataforma se produce en la posición x0=-ye, en el instante t1.
La velocidad del bloque es
vx=-g·t1
Choque elástico
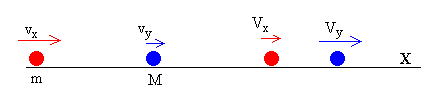
Supondremos que el bloque y la plataforma forman un sistema aislado en el momento del choque. El momento lineal se conserva. Si además el choque es elástico, la energía cinética antes y después del choque es la misma.
donde vx y Vx son las velocidades del bloque antes y después del choque, y vy y Vy son las velocidades de la plataforma antes y después del choque.
Escribimos las ecuaciones de la forma alternativa
La diferencia de los cuadrados de dos números es igual al producto de su suma por su diferencia
Nos queda un sistema de dos ecuaciones más fácil de resolver
Despejamos las velocidades del bloque Vx y de la plataforma Vy después del choque
Movimiento del bloque después del choque
En el instante t=0, (tiempo total tt=t1) el bloque parte de la posición x0=-ye, con velocidad inicial v0x=Vx
Movimiento de la plataforma después del choque.
En el instante t=0, (tiempo total tt=t1) la plataforma parte de la posición y0=-ye, con velocidad inicial v0y=Vy
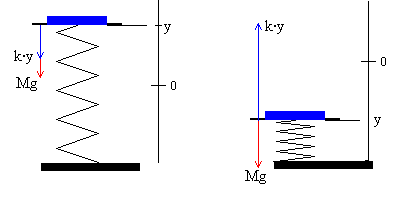
Las fuerzas sobre la plataforma son el peso y la fuerza que ejerce el muelle. La segunda ley de Newton se escribe
Ma=-ky-Mg
En forma de ecuación diferencial
La solución de esta ecuación diferencial es la suma de la solución de la ecuación diferencial homogénea
y1=Asin(ωt)+Bcos(ωt)
donde A y B son constantes que se determinan a partir de las condiciones iniciales
y de la solución particular
y2=C
Introduciendo la solución particular en la ecuación diferencial determinamos el valor de la constante C.
ω2C=-g
La solución de la ecuación diferencial completa es y=y1+y2
Las condiciones iniciales son las siguientes: la plataforma parte en el instante t=0 (tiempo total tt=t1) de la posición y0, con velocidad v0y. Resolvemos el sistema de dos ecuaciones con dos incógnitas para determinar A y B.
Segundo choque
El próximo choque se produce en el instante t2, (tiempo total tt=t1+t2) cuando coinciden la posición x del bloque y la posición y de la plataforma. Para ello, hay que resolver por procedimientos numéricos la ecuación trascendente
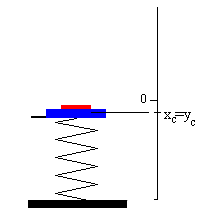
Se obtiene la raíz t2 de la ecuación y se calcula la posición xc=yc de encuentro en dicho instante.
La velocidad del bloque antes del choque es
La velocidad de la plataforma antes del choque es
Se calculan las velocidades Vx y Vy del bloque y de la plataforma después del choque. Estas son las velocidades v0x=Vx y v0y=Vy iniciales de ambos cuerpos en el instante t=0 (tiempo total tt=t1+t2) cuando se encuentran en la posición x0=xc, y0=yc calculada en el instante t2.
El bloque asciende y la plataforma oscila, vuelven a chocar y así, sucesivamente…
La energía del sistema formado por el bloque, el muelle y la plataforma en cualquier instante tt es
La energía total permanece constante
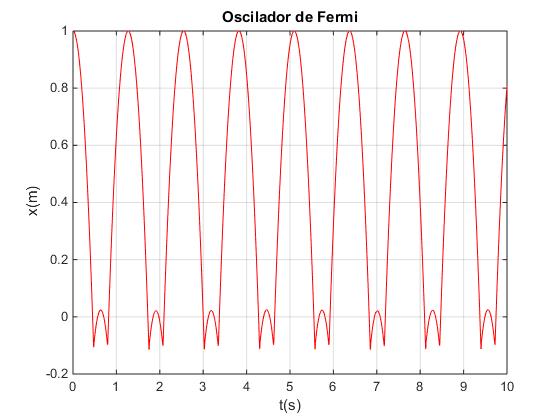
Creamos un script de MATLAB para representar la trayectoria seguida por el bloque
k=2000; %constante del muelle
m=10; %masa del bloque
M=20; %masa de la plataforma
altura=1.0; %altura inicial
ye=M*9.8/k; %equilibrio
w=sqrt(k/M);
x0=altura;% situación inicial del bloque
v0x=0;
x=x0;
y0=-ye; %situación inicial de la platforma
y=y0;
v0y=0;
t=0; %tiempo parcial
dt=0.005;
tt=0:dt:10; %tiempo total
xp=zeros(1,length(tt));
tipo=1;
for i=1:length(tt)
xp(i)=x;
t=t+dt;
switch tipo
case 1 %el boque desciende
x=x0-9.8*t^2/2;
vx=-9.8*t;
if x<-ye
vy=0.0;
vx=-sqrt(2*(x0+ye)*9.8);
x0=-ye;
y0=x0;
t=0.0;
tipo=2;
end
case 2 %choque
v0x=((m-M)*vx+2*M*vy)/(M+m);
v0y=(2*m*vx+(M-m)*vy)/(m+M);
t=0.0;
tipo=3;
case 3 %movimiento después del choque
x=x0+v0x*t-9.8*t^2/2;
y=-9.8/w^2+v0y*sin(w*t)/w+(y0+9.8/w^2)*cos(w*t);
if x<y %choque
f=@(t) -9.8/w^2+v0y*sin(w*t)/w+
(y0+9.8/w^2)*cos(w*t)-(x0+v0x*t-9.8*t^2/2);
t0=fzero(f,[t-dt,t]);
vx=v0x-9.8*t0;
vy=v0y*cos(w*t0)-(y0*w+9.8/w)*sin(w*t0);
y0=-9.8/w^2+v0y*sin(w*t0)/w+(y0+9.8/w^2)*cos(w*t0);
x0=x0+v0x*t0-9.8*t0^2/2;
t=0.0;
tipo=2;
end
end
end
plot(tt,xp, 'r')
grid on
xlabel('t(s)')
ylabel('x(m)')
title('Oscilador de Fermi')
Sensibilidad a un pequeño cambio de las condiciones iniciales
Unos de los aspectos más interesantes es el de examinar la respuesta del sistema ante un pequeño cambio de las condiciones iniciales.
Cómo evoluciona el sistema si cambiamos ligeramente la altura h desde la que se deja caer el bloque. Veamos algunos ejemplos
Modificamos el script anterior para que nos dibuje dos trayectorias del bloque para alturas iniciales próximas
k=2000; %constante del muelle
m=10; %masa del bloque
M=20; %masa de la plataforma
ye=M*9.8/k; %equilibrio
w=sqrt(k/M);
dt=0.005;
tt=0:dt:10; %tiempo total
xp=zeros(1,length(tt));
tipo=1;
hold on
color=['r','b'];
altura=[1,1.01] %dos alturas iniciales próximas
for j=1:2
t=0;
x0=altura(j);
x=x0;
v0x=0;
y0=-ye;
y=y0;
v0y=0;
for i=1:length(tt)
xp(i)=x;
t=t+dt;
switch tipo
case 1
x=x0-9.8*t^2/2;
vx=-9.8*t;
if x<-ye
vy=0.0;
vx=-sqrt(2*(x0+ye)*9.8);
x0=-ye;
y0=x0;
t=0.0;
tipo=2;
end
case 2
v0x=((m-M)*vx+2*M*vy)/(M+m);
v0y=(2*m*vx+(M-m)*vy)/(m+M);
t=0.0;
tipo=3;
case 3
x=x0+v0x*t-9.8*t^2/2;
y=-9.8/w^2+v0y*sin(w*t)/w+(y0+9.8/w^2)*cos(w*t);
if x<y %choque
f=@(t) -9.8/w^2+v0y*sin(w*t)/w+
(y0+9.8/w^2)*cos(w*t)-(x0+v0x*t-9.8*t^2/2);
t0=fzero(f,[t-dt,t]);
vx=v0x-9.8*t0;
vy=v0y*cos(w*t0)-(y0*w+9.8/w)*sin(w*t0);
y0=-9.8/w^2+v0y*sin(w*t0)/w+(y0+9.8/w^2)*cos(w*t0);
x0=x0+v0x*t0-9.8*t0^2/2;
t=0.0;
tipo=2;
end
end
end
plot(tt,xp, color(j))
end
grid on
xlabel('t(s)')
ylabel('x(m)')
title('Oscilador de Fermi')
Ejemplo 1:
- Masa del bloque m=10 kg
- Masa de la plataforma M=20 kg
- Constante elástica del muelle k=2000 N/m
En la figura, vemos la representación gráfica x-t del bloque para dos alturas iniciales distintas
- Altura inicial h=1.0 en color rojo
- Altura inicial h=1.01 en color azul
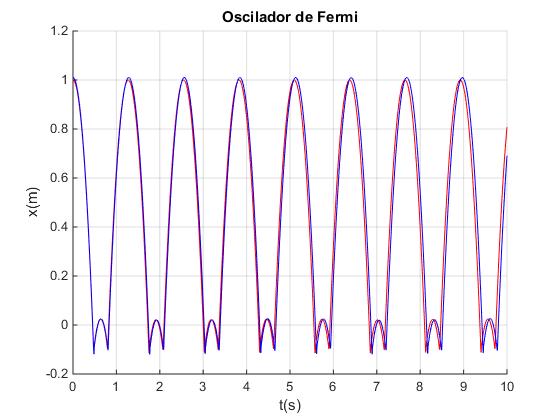
Las posiciones del bloque en el instante tt=10 s son muy parecidas
Ejemplo 2:
- Masa del bloque m=15 kg
- Masa de la plataforma M=20 kg
- Constante elástica del muelle k=2000 N/m
En la figura, vemos la representación gráfica x-t del bloque para dos alturas iniciales distintas
- Altura inicial h=1.0 en color rojo
- Altura inicial h=1.01 en color azul
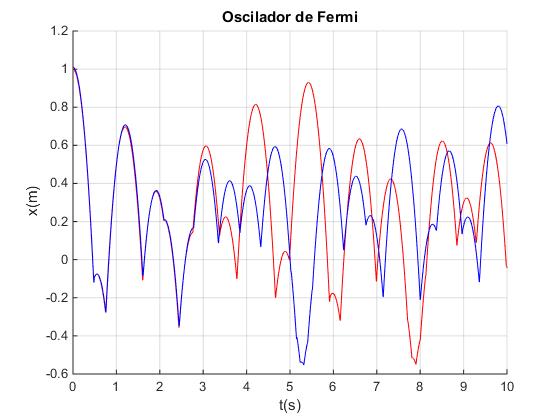
Las posiciones del bloque en el instante tt=10 s difieren bastante
En este caso, las posiciones del bloque calculadas por la simulación más abajo, difieren de las calculadas mediante el script de MATLAB, cuando el tiempo se hace grande. Esto se debe a las diferencias en el cálculo del instante de choque entre el bloque y la plataforma, se utilizan dos procedimientos numéricos diferentes para calcular la raíz de una ecuación trascendente en el intervalo especificado: el punto medio en la simulación y la función fzero, en el script
Actividades
Se introduce
-
La masa m del bloque, en el control titulado Masa bloque
-
La masa M de la plataforma, en el control titulado Masa plataforma
-
La constante elástica del muelle k, en el control titulado Constante elástica
-
La altura inicial h desde la que se suelta el bloque en el intervalo (0.95, 1.05) en el control titulado Altura inicial.
Se pulsa el botón titulado Nuevo
El programa verifica si la máxima deformación inicial que experimenta el muelle xm después de chocar por primera vez el bloque y la plataforma es superior a 0.5 m, en cuyo caso se invita al usuario a disminuir la masa del bloque o a aumentar el valor de la constante elástica.
Se pulsa el botón titulado ►
Se observa el movimiento del bloque y de la plataforma en la parte izquierda y la representación gráfica de la posición x del bloque en función del tiempo total tt .
El programa calcula en cada instante el tanto por ciento de error relativo en la energía o el cociente
donde E es la energía del sistema en cualquier instante t, y E0 es la energía inicial del sistema.
Este valor se proporciona en caracteres de color rojo en la parte inferior izquierda. Su valor debe ser siempre cero, o un valor muy pequeño lo que indica que la energía del sistema permanece constante y el programa realiza los cálculos correctamente. Si el procedimiento numérico empleado, es incapaz de resolver dos choques consecutivos muy próximos, el error se incrementa y el programa debe de interrumpirse manualmente ya que no realiza los cálculos correctamente.
Referencias
Lopac V., Dananic V. Energy conservation and chaos in the gravitationally driven Fermi oscillator. Am. J. Phys. 66 (10) October 1998, pp. 892-902

