La máquina de Zeeman
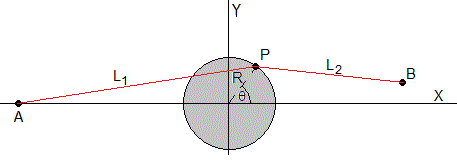
La máquina de Zeeman consiste en un disco de radio R cuyo centro está en el origen. Tomamos dos gomas elásticas iguales de longitud L0 sin deformar. Conectamos los puntos A y P con la primera goma, su longitud deformada será L1. Conectamos los puntos P y B con la segunda goma cuya longitud será ahora L2.
El punto A está en el eje X sus coordenadas son (-A,0). El punto P está en el borde del disco, sus coordenadas son (Rcosθ, Rsinθ), las coordenadas del extremo B son (X,Y).
En la teoría de catástrofes se mueve el extremo B lentamente y se observa el nuevo estado de equilibrio del sistema.
La energía potencial V del sistema formado por dos gomas iguales deformadas es
La energía cinética T de un disco de momento de inercia I girando alrededor del eje fijo Z, con velocidad angular dθ/dt es
La lagrangiana L=T-V es
La ecuación del movimiento se obtiene
Añadimos una fuerza de rozamiento proporcional a la velocidad, para que el estado transitorio desaparezca al cabo de cierto tiempo teóricamente infinito, pero en la práctica, en un tiempo limitado tanto menor cuanto mayor sea la constante de amortiguamiento λ
Dividimos todas las longitudes entre el radio R del disco: l1=L1/R, l2=L2/R, l0=L0/R, a=A/R, x=X/R, y=Y/R, y el tiempo τ=t·λ/I, quedando la ecuación diferencial expresada en términos de magnitudes adimensionales
Dada la posición (x,y) del extremo B se resuleve la ecuación diferencial por procedimientos numéricos, con las condiciones iniciales especificadas. Consideremos el siguiente caso
El extremo B describe un Movimiento Armónico Simple
Se situa el extremo B en la posición x=x0 y se hace oscilar verticalmente con amplitud y0 y frecuencia angular 2π/Tp, describiendo el Movimiento Armónico Simple y=y0sin(2πt/Tp)
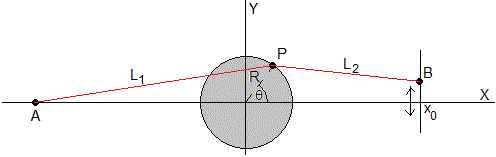
Se resuelve la ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales. En el instante t=0, θ=0 y dθ/dt=0. Esperamos un tiempo, hasta que desaparezca el estado transitorio y representamos el estado estacionario en el espacio de las fases, θ, en el eje X y dθ/dt en el eje Y.
Fijamos los parámetros del sistema (cinco primeras líneas de código) y vamos cambiando la abscisa x0=6.367 del extremo B
c=10; %constante de proporcionalidad
a=6; %abscisa del extremo A
l0=3; %longitud de las gomas sin deformar
y0=0.6; %amplitud de la oscilación
Tp=3; %periodo de la oscilación
x0=6.367; %abscisa del extremo B
xIni=[0,0]; %condiciones iniciales
f=@(t,x)[x(2); c*((sqrt((cos(x(1))+a)^2+sin(x(1))^2)-l0)
*a*sin(x(1))/sqrt((cos(x(1))+a)^2+sin(x(1))^2)+(sqrt((x0-cos(x(1)))^2+
(y0*sin(2*pi*t/Tp)-sin(x(1)))^2)-l0)*(y0*sin(2*pi*t/Tp)*cos(x(1))-x0*sin(x(1)))
/sqrt((x0-cos(x(1)))^2+(y0*sin(2*pi*t/Tp)-sin(x(1)))^2))-x(2)];
[t,x]=ode45(f,[0, 2000],xIni);
indices=find((t<1000).*t); %no se dibuja desde el tiempo t=0 a t=1000;
plot(x(indices(end):end,1),x(indices(end):end,2))
grid on
xlabel('\theta')
ylabel('d\theta/dt')
title ('Máquina de Zeeman')
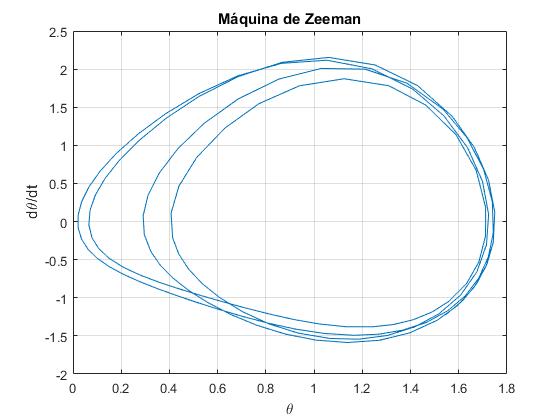
Cambiamos la abscisa x0=6.42 del extremo B y observamos la nueva trayectoria en el espacio de las fases
Actividades
Se fijan los valores de los siguientes parámetros:
- La constante c=10 de proporcionalidad (incluye el momento de inercia del disco I y la constante de amortiguamiento λ)
- La abscisa a=6 del punto A situado a la izquierda del origen, donde se fija el extremos de la primera goma
- La longitud de las gomas sin deformar, l0=3
- La amplitud y0=0.6 del Movimiento Armónico Simple que describe el extremo B
- El periodo Tp=3 del Movimiento Armónico Simple que describe el extremo B
La abscisa x0 del extremo B se puede cambiar en el control titulado Posición
Se pulsa el botón titulado Nuevo
Se espera un tiempo hasta que desaparezca el estado transitorio. Se marca la casilla titulada Gráfica para que se represente el estado estacionario en el espacio de las fases, θ, en el eje X y dθ/dt en el eje Y.

