Dos osciladores acoplados
Sea un sistema formado por dos osciladores acoplados, formado por dos partículas de masas m1 y m2 situadas en los extremos de dos muelles de constantes elásticas k1 y k3. El acoplamiento se efectúa uniendo las dos partículas mediante un muelle de constante k2, tal como se puede ver en la figura.
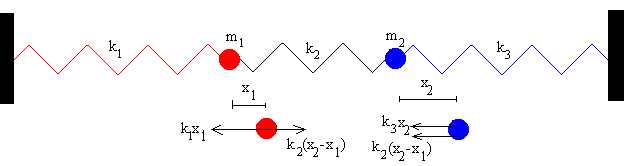
Llamemos x1 y x2 a los desplazamientos de cada una de las partículas a partir de su posición de equilibrio, medidos como positivos cuando están a la derecha. El muelle de la izquierda se ha estirado x1, el de la derecha se ha comprimido x2 y el central se ha deformado x2-x1. Las fuerzas sobre cada una de las partículas se indican en la figura.
- Sobre la partícula de la izquierda, se ejerce una fuerza hacia la izquierda k1x1 y una fuerza hacia la derecha debida a la deformación del muelle central k2(x2-x1), suponemos que x2 es mayor que x1.
- Sobre la partícula derecha, se ejerce una fuerza hacia la izquierda k3x2 y otra fuerza hacia la izquierda debida a la deformación del muelle central k2(x2-x1)
El muelle central ejerce fuerzas iguales y de sentido contrario sobre cada una de las partículas.
Aplicamos la segunda ley de Newton a cada una de las partículas, y escribimos las ecuaciones del movimiento en forma de ecuaciones diferenciales de segundo orden
En forma matricial
Buscamos una solución de la forma
x1=X1sin(ωt+φ), x2=X2sin(ωt+φ)
que representa MAS de amplitud X1, X2 y frecuencia angular ω.
Tenemos un sistema homogéneo, los cuadrados de las frecuencias de los modos normales de vibración se calculan haciendo que el determinante de los coeficientes sea igual a cero
Obtenemos una ecuación de segundo grado en ω2 con dos raíces. Para cada una de las dos frecuencias angulares ω1 y ω2 el sistema homogéneo nos proporciona una relación entre X1 y X2 que denominaremos r1 y r2.
El movimiento resultante de cada una de las partículas x1 y x2 es la combinación lineal de los dos modos normales de vibración de frecuencias angulares ω1 y ω2
A partir de las condiciones iniciales
determinamos las constantes desconocidas, amplitudes y fases:
Ejemplo
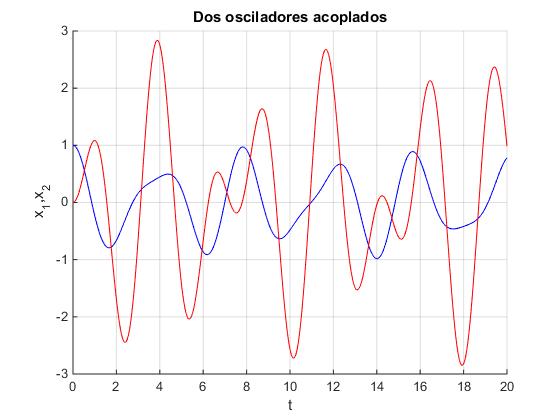
Vamos a determinar la respuesta del sistema formado por dos partículas de masas m1=10 y m2=1 unidas por muelles de constantes k1=30, k2=5 y k3=0. Las condiciones iniciales en el instante t=0, son las siguientes: posición inicial x01=1, x02=0, velocidad inicial v01=0, v02=0.
% dos osciladores acoplados
k1=30; k2=5; k3=0;
m1=10; m2=1;
%cuadrado de las frecuencias de los modos normales de oscilación
a=(k1+k2)/m1+(k2+k3)/m2;
b=((k1+k2)*(k2+k3)-k2^2)/(m1*m2);
w2=roots([1,-a,b])
r(1)=(k1+k2-m1*w2(1))/k2;
r(2)=(k1+k2-m1*w2(2))/k2;
%condiciones iniciales
X0=[1,0];
V0=[0,0];
X1_sin=(r(2)*X0(1)-X0(2))/(r(2)-r(1));
X1_cos=(r(2)*V0(1)-V0(2))/(sqrt(w2(1))*(r(2)-r(1)));
X2_sin=(r(1)*X0(1)-X0(2))/(r(1)-r(2));
X2_cos=(r(1)*V0(1)-V0(2))/(sqrt(w2(2))*(r(1)-r(2)));
X1=sqrt(X1_sin^2+X1_cos^2);
fi1=atan2(X1_sin,X1_cos);
X2=sqrt(X2_sin^2+X2_cos^2);
fi2=atan2(X2_sin,X2_cos);
%ecuación del movimiento de las partículas
t=linspace(0,20,400);
x1=X1*sin(sqrt(w2(1))*t+fi1)+X2*sin(sqrt(w2(2))*t+fi2);
x2=r(1)*X1*sin(sqrt(w2(1))*t+fi1)+r(2)*X2*sin(sqrt(w2(2))*t+fi2);
%representación gráfica
hold on
plot(t,x1,'b');
plot(t,x2,'r');
title('Dos osciladores acoplados')
ylabel('x_1,x_2')
xlabel('t')
grid on
hold off
En la ventana de comandos aparecen los cuadrados de las frecuencias de los modos normales de vibración
w2 =
6.0000
2.5000
Modos normales de vibración
El caso más sencillo es aquél en el que k1=k3=k y m1=m2=m.Las partículas tienen masa m y las constantes elásticas de sus muelles son iguales a k. El muelle que acopla a las dos partículas tiene constante k2.
Tenemos un sistema homogéneo del tipo (A-λI)X=0, donde I es la matriz unidad. Los cuadrados de las frecuencias de los modos normales de vibración son los valores propios λ=ω2 de la matriz A.
Calculamos mediante la función
>> syms k k2 m; >> A=[(k+k2)/m,-k2/m;-k2/m,(k+k2)/m]; >> [V,D]=eig(A) V = [ 1, -1] [ 1, 1] D = [ k/m, 0] [ 0, (k + 2*k2)/m]
Los valores propios λ=ω2 (cuadrado de las frecuencias angulares) están en la diagonal de la matriz D.
Sus correspondientes vectores propios son los vectores columna de la matriz V.
- El vector propio correspondiente al primer valor propio es
o simplemente [1;1]
- El vector propio correspondiente al segundo valor propio es
o simplemente [1;-1] ó [-1;1]
La ecuación del movimiento de cada una de las partículas es la superposición de los modos normales de vibración
Teniendo en cuenta la relación entre amplitudes
A partir de las condiciones iniciales
determinamos las constantes desconocidas
Que para este caso son
- El primer modo normal de vibración de frecuencia ω1 se obtiene cuando X(2)=0 o bien, cuando x01=x02 y v01=v02. Los dos osciladores se mueven en fase, el muelle central no sufre ninguna deformación y por tanto, no ejerce ninguna fuerza sobre las partículas, las cuales se mueven como si no estuvieran acopladas.
- El segundo modo normal de vibración se obtiene cuando X(1)=0 es decir, cuando x01=-x02 y v01=-v02. Los dos osciladores se mueven en oposición de fase.
Ejemplo
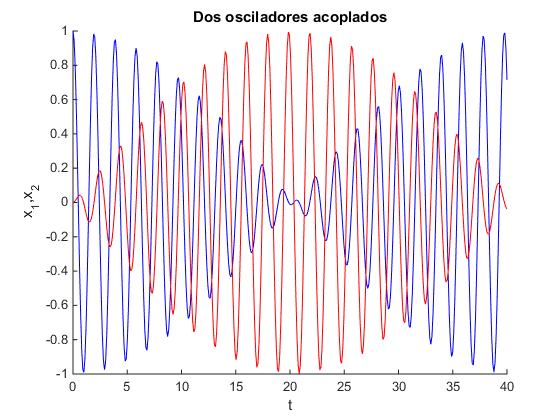
Supongamos que la constante de los muelles es k=10 y la constante del acoplamiento k2=0.5, la masa m=1 de ambas partículas. Se desvía la primera partícula x01=1 de la posición de equilibrio y se suelta. Vamos a determinar el movimiento de cada partícula.
% dos osciladores acoplados
k=10; k2=0.5; k=10;
m=1;
%calcula las frecuencias de los modos normales de vibración
A=[(k+k2)/m,-k2/m;-k2/m,(k+k2)/m];
[V,D]=eig(A);
%frecuencias de los modos normales de vibración
w1=sqrt(D(1,1)); w2=sqrt(D(2,2));
%calcula las amplitudes X1, X2 y
%fases fi1, fi2 a partir de las condiciones iniciales
x01=1; x02=0;
v01=0; v02=0;
X_sin1=(x01+x02)/2;
X_sin2=(x01-x02)/2;
X_cos1=(v01+v02)/(2*w1);
X_cos2=(v01-v02)/(2*w2);
X1=sqrt(X_sin1^2+X_cos1^2);
X2=sqrt(X_sin2^2+X_cos2^2);
fi1=atan2(X_sin1,X_cos1);
fi2=atan2(X_sin2,X_cos2);
%representación gráfica
t=linspace(0,40,400);
x1=X1*sin(w1*t+fi1)+X2*sin(w2*t+fi2);
x2=X1*sin(w1*t+fi1)-X2*sin(w2*t+fi2);
hold on
plot(t,x1,'b');
plot(t,x2,'r');
title('Dos osciladores acoplados')
ylabel('x_1,x_2')
xlabel('t')
hold off
Estudio energético
La energía total del sistema es la suma de las energías cinética y potencial. Tenemos la energía cinética de cada una de las partículas, la energía potencial elástica del muelle izquierdo que se deforma x1, del muelle derecho que se deforma x2, y del muelle central que se deforma x2-x1.
Una vez agrupados los términos, el primer paréntesis depende solamente de x1 y puede denominarse la energía del primer oscilador, el segundo término depende solamente de x2 y puede llamarse energía del segundo oscilador. El último término, que depende de x1 y x2 se denomina energía de acoplamiento o de interacción. Este término es el que describe el intercambio de energía entre los dos osciladores.
Actividades
Se introduce:
- la constante elástica de los dos osciladores, en el control titulado Cte. muelles.
- la constante elástica del muelle central, en el controltitulado Cte. acoplamiento
- la masa de las partículas se ha tomado como la unidad.
- la posición inicial de la partícula de la izquierda (una cantidad menor o igual que la unidad), en el control titulado Posición inicial de 1
- la posición inicial de la partícula de la derecha, en el control titulado Posición inicial de 2.
- las velocidades iniciales se toman como cero.
Se pulsa el botón titulado Nuevo
Modos normales de vibración
- Primer modo normal de oscilación: introducir la misma cantidad, por ejemplo, 1.0 en los controles titulados Posición inicial 1 y Posición inicial 2.
- Segundo modo normal: introducir la misma cantidad pero con signos opuestos en dichos controles, por ejemplo, 1.0 en Posición inicial 1, y –1.0 en Posición inicial 2.