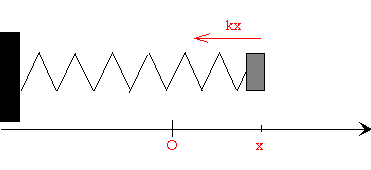
Cuando una partícula se desplaza x de la posición de equilibrio, actúa sobre ella una fuerza que es proporcional al desplazamiento x y de sentido contrario a éste, tal como se muestra en la figura.

La ecuación del movimiento se escribe

ma=-kx

Teniendo en cuenta que la aceleración es la derivada segunda de la posición x, expresamos la ecuación del movimiento como ecuación diferencial de segundo orden.

${\displaystyle \frac{d^{2}x}{d{t}^2}+{\omega }_0^{2}x=0{\omega }_{\text{0}}^{\text{2}}=\frac{k}{m}}$

ω₀ se denomina frecuencia propia o natural del oscilador armónico.

La ventaja de expresar las oscilaciones en términos de una ecuación diferencial es que podemos establecer analogías entre sistemas físicos oscilantes completamente diferentes: mecánicos, eléctricos, hidráulicos, etc.

La solución de esta ecuación diferencial es

${\displaystyle \begin{array}{l}x=A\sin ({\omega }_{0}t)+B\cos ({\omega }_{0}t)\\ v=\frac{dx}{dt}={\omega }_0\left(A\cos ({\omega }_{0}t)-B\sin ({\omega }_{0}t)\right)\end{array}}$

Las constantes A y B se determinan a partir de la posición inicial x₀ y la velocidad inicial v₀ en el instante t=0.

${\displaystyle \begin{array}{l}t=0\{\begin{array}{l}{x}_0=B\\ v_0={\omega }_{0}A\end{array}\\ x=\frac{v_0}{{\omega }_0}\sin ({\omega }_{0}t)+x_0\cos ({\omega }_{0}t)\end{array}}$

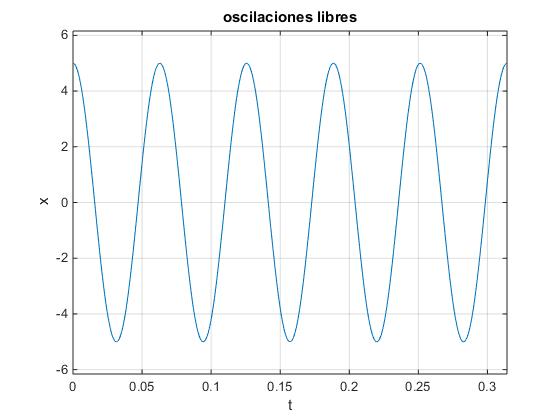
Sea un oscilador de frecuencia angular ω₀=100 rad/s. Sabiendo que la partícula parte de la posición x₀=5 con velocidad inicial nula, v₀=0, obtener y representar su posición x en función del tiempo t

O bien, de forma equivalente, x=A·sin(ω₀t+φ), donde A es la amplitud y φ la fase inicial

${\displaystyle A=\sqrt{\frac{v_0^2}{{\omega }_0^2}+x_0^2}\tan \phi =\frac{x_0{\omega }_0}{v_0}}$

>> syms w0 x0 v0;
>> x=dsolve('D2x+w0^2*x=0','x(0)=x0','Dx(0)=v0');
>> x=simplify(x)
x =x0*cos(t*w0) + (v0*sin(t*w0))/w0
>> xx=subs(x,{w0 x0 v0},{100 5 0})
xx =5*cos(100*t)
>> ezplot(xx,[0 0.1*pi])
>> xlabel('t')
>> ylabel('x')
>> title('oscilaciones libres')
>> grid on

Trayectoria en el espacio de las fases

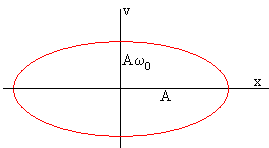
El espacio de las fases nos muestra otra perspectiva del comportamiento de un oscilador. Se representa el momento lineal (o la velocidad) v en el eje vertical, y la posición del móvil x en el eje horizontal.

x=A·sin(ω₀t+φ)
v=A·ω_0·cos(ω₀t+φ)

Eliminando el tiempo t en estas dos ecuaciones, obtenemos la ecuación de la trayectoria, una elipse.

${\displaystyle \frac{x^2}{A^2}+\frac{y^2}{{(A{\omega }_0)}^2}=1}$

Energía del oscilador

La característica esencial de una oscilación libre es que la amplitud se mantiene constante y por tanto, la energía total se mantiene constante.

${\displaystyle \begin{array}{l}E=\frac{1}{2}m{v}^2+\frac{1}{2}k{x}^2=\frac{1}{2}m{v}^2+\frac{1}{2}m{\omega }_0^2{x}^2=\\ \frac{1}{2}m\left(v_0^2+x_0^2{\omega }_0^2\right)\end{array}}$

Actividades

Se introduce

• la posición inicial x₀, en el control titulado Posición
• la velocidad inicial del móvil v₀, en el control titulado Velocidad.
• la frecuencia angular se ha fijado en ω₀ =100 rad/s.

Se pulsa en el botón Nuevo.