El oscilador forzado
El estado transitorio y su evolución hacia el estado estacionario
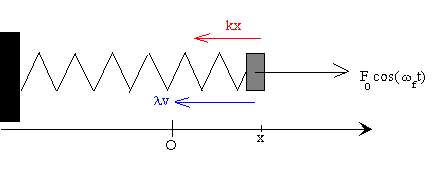
Las fuerzas que actúan sobre la partícula son:
- La fuerza que ejerce el muelle, -k·x
- La fuerza de rozamiento proporcional a la velocidad λv y de sentido contrario a ésta
- La fuerza oscilante F0·cos(ωf t) de frecuencia angular ωf
La ecuación del movimiento de la partícula es
ma=-kx-λv+F0·cos(ωf t)
Expresamos la ecuación del movimiento en forma de ecuación diferencial que describe las oscilaciones forzadas
- donde ω0 es la frecuencia natural o propia del oscilador
- ωf es la frecuencia angular de la fuerza oscilante de amplitud F
- γ es la constante de amortiguamiento, γ<ω0
La solución general de la ecuación diferencial homogénea tiene la forma
Donde los coeficientes C y D se determinan a partir de las condiciones iniciales
Supondremos inicialmente que ω0≠ωf
Una solución particular de la ecuación diferencial completa tiene la forma
x2=Acos(ωf t)+Bsin(ωf t)
Obtendremos los valores de A y B haciendo que cumpla la ecuación diferencial lineal completa
La solución general de la ecuación diferencial completa es la suma de la solución general de la homogénea más la solución particular x=x1+x2.
El primer término, describe el estado transitorio. El segundo término, describe el estado estacionario.
La velocidad vale
No hay rozamiento γ=0
Cuando ω0≠ωf
La solución de la ecuación diferencial para las condiciones iniciales: en el instante t=0, la posición es x0 y la velocidad v0, se escriben.
.
Establecemos los siguientes valores:
- Cociente F/m=1
- Frecuencia angular propia, ω0=100 rad/s y
- Frecuencia de la fuerza oscilante, ωf=120 rad/s
>> syms t w0 wf F x0 v0;
>> x=dsolve('D2x+w0^2*x=F*cos(wf*t)','x(0)=x0','Dx(0)=v0');
>> x=simplify(x)
x =(w0*(F*cos(t*w0) - F*cos(t*wf)) - v0*w0^2*sin(t*w0) +
v0*wf^2*sin(t*w0))/(w0*wf^2 - w0^3) + x0*cos(t*w0)
En el instante t=0, x0=0, v0=0, parte del origen en reposo
wf=120; %frecuencia de la fuerza oscilante
w0=100; %frecuencia natural
x=@(t) (cos(wf*t)-cos(w0*t))/(w0^2-wf^2);
fplot(x,[0,0.2*pi])
grid on
xlabel('t')
ylabel('x')
title('Sin rozamiento')
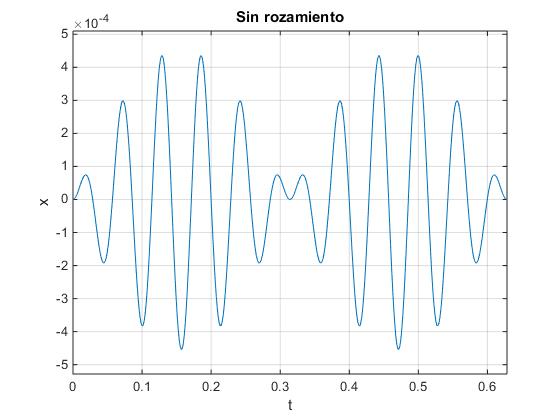
Obtenemos pulsaciones, suma de armónicos de dos frecuencias distintas
Cuando ω0=ωf
Cuando la frecuencia de la fuerza oscilante ωf se hace igual a la frecuencia propia del oscilador ω0, en el tercer término de la ecuación que nos da la posición x tenemos una ideterminación del tipo 0/0.
>> syms w0 wf t; >> limit((cos(wf*t)-cos(w0*t))/(w0^2-wf^2),wf,w0) ans =(t*sin(t*w0))/(2*w0)
O bien, resolvemos de nuevo la ecuación diferencial con ωf=ω0. Establecemos los siguientes valores:
- Coeficiente de rozamiento γ=0;
- Frecuencia angular propia y de la fuerza oscilante, ω0=100 rad/s
>> syms w0 F x0 v0;
>> x=dsolve('D2x+w0^2*x=F*cos(w0*t)','x(0)=x0','Dx(0)=v0');
>> x=simplify(x)
x =x0*cos(t*w0) + (v0*sin(t*w0))/w0 + (F*t*sin(t*w0))/(2*w0)
En el instante t=0, x0=0, v0=0, parte del origen en reposo
wf=100; %frecuencia de la fuerza oscilante
w0=100; %frecuencia natural
x=@(t) t.*sin(w0*t)/(2*w0);
fplot(x,[0,0.3*pi])
grid on
xlabel('t')
ylabel('x')
title('Sin rozamiento')
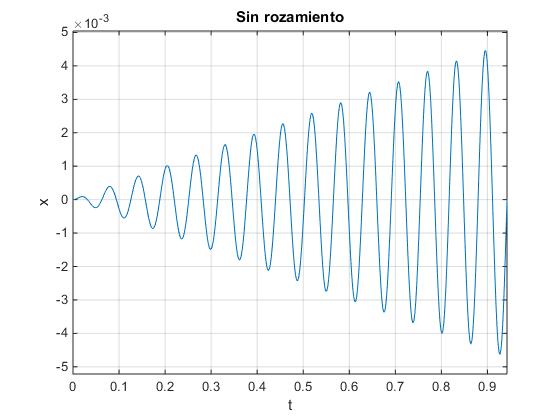
La amplitud crece linealmente sin límite
Rozamiento γ<ω0
Si las condiciones iniciales son t=0, x=x0, v=v0.
Las condiciones iniciales más sencillas son x=0, y dx/dt=0 en el instante t=0. La partícula de masa m parte del origen con velocidad inicial nula.
La posición de la partícula x que experimenta una oscilación forzada en función del tiempo t es
Cuando ω0≠ωf
Establecemos los siguientes valores:
- Coeficiente de rozamiento γ=7;
- Frecuencia angular propia, ω0=100 rad/s y
- Frecuencia de la fuerza oscilante, ωf=120 rad/s
wf=120; %frecuencia de la fuerza oscilante
w0=100; %frecuencia natural
gamma=7; %amortiguamiento
w=sqrt(w0^2-gamma^2);
x=@(t) ((w0^2-wf^2)*(cos(wf*t)-exp(-gamma*t).*cos(w*t))+
2*gamma*wf*(sin(wf*t)-(w0^2+wf^2)*exp(-gamma*t).*sin(w*t)/(2*w*wf)))
/((w0^2-wf^2)^2+4*gamma^2*wf^2);
fplot(x,[0,0.3*pi])
grid on
xlabel('t')
ylabel('x')
title('Con rozamiento')
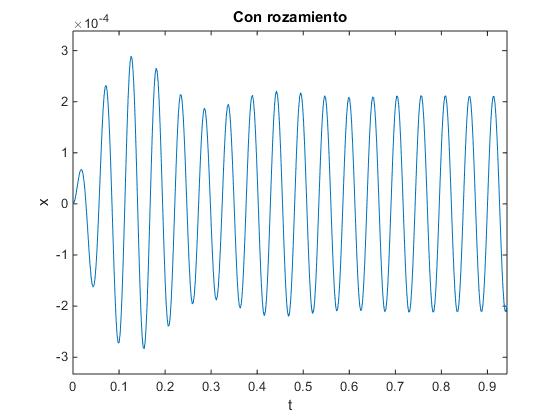
Al cabo de un cierto tiempo (teóricamente infinito) el estado transitorio desaparece y la amplitud de la oscilación forzada tiende hacia un valor constante.
Cuando ω0=ωf
Establecemos los siguientes valores:
- Coeficiente de rozamiento γ=7;
- Frecuencia angular propia y de la fuerza oscilante, ω0=ωf=100 rad/s
wf=100; %frecuencia de la fuerza oscilante
w0=100; %frecuencia natural
gamma=7; %amortiguamiento
w=sqrt(w0^2-gamma^2);
x=@(t) (sin(wf*t)-wf*exp(-gamma*t).*sin(w*t)/w)/(2*gamma*wf);
fplot(x,[0,0.3*pi])
grid on
xlabel('t')
ylabel('x')
title('Con rozamiento')
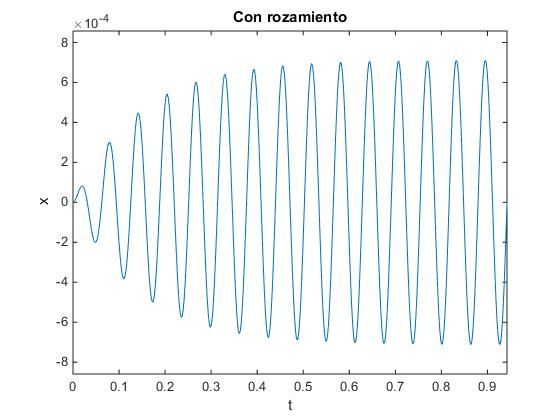
La amplitud de la oscilación crece y tiende hacia un valor límite constante
Actividades
Se introduce
- la posición inicial x0, en el control titulado Posición
- la velocidad inicial del móvil v0, en el control titulado Velocidad.
- la constante de amortiguamiento γ, en el control titulado Amortiguamiento
- la amplitud F de la fuerza oscilante, en el control titulado Amplitud
- La frecuencia angular ωf de la fuerza oscilante, en el control titulado Frecuencia
- la frecuencia angular natural del oscilador ω0=100 rad/s no se puede modificar
Se pulsa en el botón Nuevo.
Se observa la posición del móvil en función del tiempo
Ejemplos de oscilaciones forzadas
La amplitud F de la fuerza oscilante nos permite variar la escala vertical de la representación gráfica. Si la posición x(t) crece más allá de los límites de la ventana, se reduce el valor de la amplitud F en el control correspondiente.
La frecuencia propia del oscilador en ω0=100 rad/s, no se puede cambiar, pero se puede variar la frecuencia de la fuerza oscilante ωf alrededor de dicha frecuencia.
Observar y describir cada una de las representaciones
Dos opciones se presentan para el estudio completo de las oscilaciones forzadas.
- Condiciones iniciales fijadas de antemano en (x=0, v=0), el móvil se encuentra en el origen en el instante inicial.
- Condiciones iniciales que puede seleccionar el usuario del programa. Se trata de comprobar que el estado transitorio depende de las condiciones iniciales, pero no el estado estacionario (el que describe el comportamiento del oscilador, después de un cierto tiempo, teóricamente infinito. En la práctica, un intervalo de tiempo tanto más pequeño cuanto mayor sea la constante de amortiguamiento).
Condiciones iniciales fijadas de antemano en (x=0, v=0),
- Cerca de la resonancia ωf=110 y 90
- En la resonancia ωf=100
- Observar pulsos, para ωf=80 y γ=1.
Condiciones iniciales fijadas por el usuario
- Con rozamiento (γ=10)
- x=-5, v=0
- x=+5, v=0
- x=0, v=+500
- x=0, v=-500
- x=-5, v=0
- x=+5, v=0
- x=0, v=+500
- x=0, v=-500
- Sin rozamiento (γ =0)
- x=1.5, v=0
- x=0, v=-50
- x=0, v=150
- x=5, v=0
- x=0, v=-10
Ejemplos de condiciones iniciales en la resonancia (ωf =100)
Ejemplos de condiciones iniciales en las proximidades de la resonancia (ωf =90)
Ejemplos de condiciones iniciales en la resonancia (ωf =100)
Ejemplos de condiciones iniciales en las proximidades de la resonancia (ωf =90)
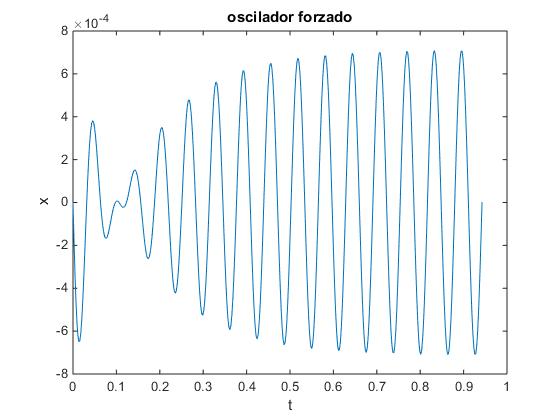
Solución numérica
Escribimos la ecuación diferencial de segundo orden que describe las oscilaciones forzadas en forma de dos ecuaciones diferenciales de primer orden, para resolverlas utilizando la función ode45 de MATLAB
Si a la frecuencia de la fuerza oscilante ωf le damos los valores wf=120 y wf=100 obtenemos las mismas figuras que resolviendo la ecuación diferencial de forma analítica.
w0=100; %frecuencia angular propia
g=7; %rozamiento, gamma,
wf=100; %frecuencia de la fuerza oscilante (cambiar este valor)
F=1; %F0/m amplitud de la fuerza oscilante
%condiciones iniciales
x0=[0,-0.08]; %posición inicial, x0, velocidad inicial, v0
tf=0.3*pi; %tiempo final
f=@(t,x) [x(2);-2*g*x(2)-w0*w0*x(1)+F*cos(wf*t)];
tspan=[0 tf];
[t,x]=ode45(f,tspan,x0);
plot(t,x(:,1))
xlabel('t')
ylabel('x');
title('oscilador forzado')
En este ejemplo, ωf=100. Las condiciones iniciales son: x0=0, v0=-0.08. El estado transitorio cambia, pero no lo hace la amplitud constante de la oscilación que se establece al cabo de un cierto tiempo (teóricamente infinito)