Ecuaciones del movimiento

• Movimiento del pistón

El pistón describe un MAS de amplitud A y frecuencia angular ω. En el instante inicial t=0, el pistón parte del origen. Su posición y velocidad en función del tiempo t es

y_p=A·sin(ωt)
v_p= A·ω·cos(ωt)

• Movimiento de la bola

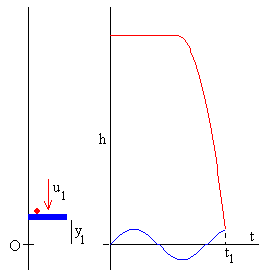
La bola se deja caer desde una altura h, con velocidad inicial nula en el instante t₀. Su posición y velocidad en el instante t son

y_b=h-g(t-t₀)²/2
v_b= -g(t-t₀)

Primer choque entre la bola y el pistón

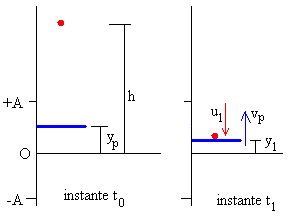
El encuentro entre el pistón y la bola se produce en la posición y₁ y en el instante t₁ tal que y_b=y_p. Para determinar el instante t₁, tenemos que resolver por procedimientos numéricos la ecuación trascendente

h-g(t-t₀)²/2= A·sin(ωt)

Inmediatamente antes del choque, la posición y velocidad de la bola son

y₁=h-g(t₁-t₀)²/2
u₁= -g(t₁-t₀)

La velocidad del pistón se supone que no cambia cuando choca con la bola, de modo que su velocidad antes y después del choque es

v_p= A·ω·cos(ωt₁)

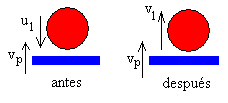
De la definición de coeficiente de restitución e, determinamos la velocidad de la bola v₁ inmediatamente después del choque

v₁-v_p=-e(u₁-v_p)

v₁=(1+e)·A·ω·cos(ωt₁)+eg(t₁-t₀)

Esta es la velocidad inicial de la bola en su movimiento vertical hacia arriba y hacia abajo hasta el próximo choque con el pistón.

Después del choque

La posición y la velocidad de la bola en el intervalo t₁<t<t₂ serán

y_b=y₁+v₁(t-t₁)-g(t-t₁)²/2
v_b=v₁-g(t-t₁)

Segundo choque entre la bola y el pistón

El segundo choque se produce en la posición y₂ y en el instante t₂ tal que y_b=y_p. Para determinar el instante t₂, tenemos que resolver por procedimientos numéricos la ecuación trascendente

y₁+v₁(t-t₁)-g(t-t₁)²/2=A·sin(ωt)

La velocidad del pistón se supone que no cambia cuando choca con la bola, de modo que la velocidad antes y después del choque es

v_p= A·ω·cos(ωt₂)

La posición y velocidad de la bola inmediatamante antes del choque son

y₂=y₁+v₁(t₂-t₁)-g(t₂-t₁)²/2
u₂= v₁-g(t₂-t₁)

La velocidad de la bola después del choque es

v₂=(1+e)·A·ω·cos(ωt₂)-e(v₁-g(t₂-t₁))

Después del choque

La posición y la velocidad de la bola en el intervalo t₂<t<t₃ serán

y_b=y₂+v₂(t-t₂)-g(t-t₂)²/2
v_b=v₂-g(t-t₂)

Choque n entre la bola y el pistón

El movimiento de la bola después del choque n

y_b=y_n+v_n(t-t_n)-g(t-t_n)²/2

Choque

El instante t_n+1 y la posición y_n+1 en el momento del siguiente choque se determina resolviendo la ecuación trascendente por procedimientos numéricos

y_n+v_n(t-t_n)-g(t-t_n)²/2= A·sin(ωt)

La velocidad del pistón se supone que no cambia cuando choca con la bola, de modo que la velocidad antes y después del choque es

v_p= A·ω·cos(ωt_n+1)

La posición y velocidad de la bola inmediatamente antes del choque son

y_n+1=y_n+v_n(t_n+1-t_n)-g(t_n+1-t_n)²/2
u_n+1= v_n-g(t_n+1-t_n)

La velocidad de la bola después del choque es

v_n+1=(1+e)·A·ω·cos(ωt_n+1)-e(v_n-g(t_n+1-t_n))

Después del choque

El movimiento de la bola después del choque n+1 es

y_b=y_n+1+v_n+1(t-t_n+1)-g(t-t_n+1)²/2
v_b=v_n+1-g(t-t_n+1)

El proceso iterativo se detiene cuando el intervalo de tiempo t_n+1-t_n entre dos choques consecutivos es menor que el paso dt, utilizado para mover la partícula y el pistón. El programa interactivo es entonces, incapaz de determinar el tiempo del siguiente choque.

La bola puede continuar rebotando sobre el pistón o bien, puede quedar pegada al pistón. En la página titulada "Caída libre y sucesivos rebotes" hemos demostrado que una bola que rebota sobre un plano horizontal precisa un tiempo finito para llegar al reposo después de infinitos rebotes. Si la aceleración del pistón -Aω²·sin(ωt) es mayor que la aceleración de la gravedad, la partícula no se pega al pistón, aunque podría rebotar y volver de nuevo al reposo sobre el pistón en un tiempo finito menor que el periodo de oscilación.

Sincronización

La cuestión que se plantea ahora es la de determinar la altura y₀=h, y el instante t₀, en el que se deja caer la bola para que el periodo P=t_n+1-t_n de la bola, el tiempo entre dos choques consecutivos, coincida con el periodo P=2π/ω de la oscilación del pistón (en color azul en la figura).

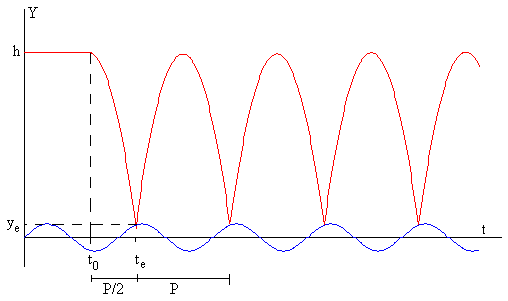
Para ello, los choques tendrán lugar en la misma posición y_e=y_b=y_p,

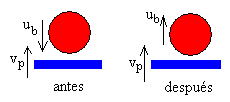
La velocidad u_b de la bola antes y después del choque con el pistón debe de ser la misma, pero cambiada de signo.

En otras palabras, la energía que pierde la bola en el choque como consecuencia de su inelasticidad debe ser igual a la ganancia en energía cinética después del impacto.

u_b-v_p=-e(-u_b-v_p)

${\displaystyle v_p=\frac{1-e}{1+e}{u}_b}$

Como la bola sale y llega a la misma posición empleando un tiempo de vuelo P, su velocidad antes y después del choque valdrá

${\displaystyle u_b=\frac{1}{2}gP=\frac{\pi g}{\omega }}$

Para alcanzar esta velocidad, la bola tiene que partir de la altura h, de modo que llegue a la posición y_e de choque con velocidad u_b empleando un tiempo P/2

${\displaystyle h=y_e+\frac{1}{2}g{\left(\frac{P}{2}\right)}^2=y_e+\frac{{\pi }^{2}g}{2{\omega }^2}}$

Como el pistón parte del origen en el instante inicial t=0, alcanzando una velocidad v_p= A·ω·cos(ωt_e) en el instante t_e del choque

${\displaystyle t_e=\frac{1}{\omega }\arccos \left(\frac{v_p}{A\omega }\right)=\frac{1}{\omega }\arccos \left(\frac{1-e}{1+e}·\frac{\pi g}{A{\omega }^2}\right)=\frac{\text{1}}{\omega }\text{arccos(}k)}$

La posición de encuentro es y_e=y_b=y_p=A·sin(ωt_e)

${\displaystyle y_e=A\sqrt{1-{\cos }^2(\omega t_e)}=A\sqrt{1-\frac{v_p^2}{A^2{\omega }^2}}=A\sqrt{1-k^2}}$

La bola se debe liberar con velocidad inicial cero, desde la altura

${\displaystyle h=\frac{{\pi }^{2}g}{2{\omega }^2}+y_e=\frac{{\pi }^{2}g}{2{\omega }^2}+A\sqrt{1-k^2}}$

En el instante t₀ tal que el tiempo de vuelo hasta que se encuentra con el pistón sea P/2, es decir, t_e-t₀=P/2

${\displaystyle t_0=\frac{\arccos k-\pi }{\omega }}$

Puesto que k<1 la amplitud A tiene que cumplir la siguiente condición

${\displaystyle A>\left(\frac{1-e}{1+e}\right)\frac{\pi g}{{\omega }^2}}$

Actividades

Se introduce

• El coeficiente de restitución e, en el control de edición titulado Coef. restitución.

• El periodo P=2π/ω del M.A.S. que describe el pistón, en el control titulado Periodo.

• La amplitud de dicho MAS se ha fijado en A=0.1 m=10 cm

• La altura inicial h, en el control titulado Altura inicial.

• El instante t₀ que se deja caer la bola, en el control titulado Tiempo inicial.

Se pulsa el botón titulado Nuevo

Se sitúa la bola en la altura inicial h, y el pistón empieza a moverse entre las posiciones –A y +A. Cuando trasncurre un tiempo t₀, la bola se deja caer

Se observa el movimiento de caída de la bola y los sucesivos rebotes sobre el pistón. En la parte derecha, se representa la posición de la bola y del pistón en función del tiempo t.

Ejemplo:

Introducimos los siguientes datos

• El coeficiente de restitución e=0.9
• La altura inicial h=1.32 m
• El periodo P=1.0 s
• El tiempo de caída t₀=0.69 s

Se pulsa el botón titulado Nuevo

Observamos el movimiento del pistón, la bola permanece en su posición inicial, después de un tiempo t₀=0.69 s la bola cae sobre el pistón

• La bola cae y choca con el émbolo en el instante t₁=1.19 s

• La posición del pistón y de la bola es y₁=0.1·sin(2π·t₁)=0.09 m, o bien, y₁=1.32-4.9·(1.186-0.69)²=0.09 m

• La velocidad antes del choque es u₁=-9.8·(1.19-0.69)=-4.9 m/s

• La velocidad del pistón antes y después del choque es v_p=0.1·2π·cos(2π·t₁)=0.23 m/s

• La velocidad de la bola después del choque se calcula a partir de la definición de coeficiente de restitución v₁-v_p=-e(u₁-v_p)

v₁=(1+0.9)·0.23+0.9·4.9=4.85 m/s

• La bola alcanza la altura máxima en el instante en el que su velocidad sea cero.

0=4.85-9.8·(t-1.19)    t=1.68 s

h=1.29 m

Se vuelve a repetir de nuevo proceso, para calcular el instante en el que se produce el segundo choque, y así sucesivamente.

Sincronización

Con los datos

• El coeficiente de restitución e=0.9
• El periodo P=1.0 s

Calculamos la altura h y el instante t₀ en el que debe se soltar la bola

La frecuencia angular ω=2π/P=2π rad/s

el parámetro k vale

${\displaystyle k=\left(\frac{1-e}{1+e}\right)\frac{\pi g}{A{\omega }^2}=\left(\frac{1-0.9}{1+0.9}\right)\frac{\pi ·9.8}{0.1·4{\pi }^2}=0.41}$

la bola se debe liberar con velocidad inicial cero, desde la altura

${\displaystyle h=\frac{{\pi }^{2}g}{2{\omega }^2}+A\sqrt{1-k^2}h=\frac{{\text{π}}^{\text{2}}\text{9}\text{.8}}{{\text{2·4·π}}^{\text{2}}}+\text{0}\text{.1}\sqrt{\text{1}-\text{0}{\text{.41}}^{\text{2}}}=1.32\text{m}}$

en el instante inicial t₀

${\displaystyle t_0=\frac{\arccos k-\pi }{\omega }{t}_0=\frac{\arccos 0.41-\pi }{2\pi }=-0.31\text{s}}$

Se obtiene el mismo resultado si la bola se libera en el instante t₀ que en el instante t₀ más un número de periodos P, por ejemplo, en el instante t₀=1-0.31=0.69, 1.69 s, etc.

Para observar la sincronización se introduce

• Coeficiente de restitución e=0.90
• Periodo P=1.0 s
• Altura inicial h=1.32 m
• El tiempo de caída t₀=0.69 s

Se pulsa el botón titulado Nuevo

Observamos que el pistón se pone en movimiento oscilando entre las posiciones +10 y -10 cm, la bola cayendo a partir del instante t₀=0.69 s

La ruta hacia el caos

Vamos a examinar el comportamiento de la bola, después de efectuar N choques con el pistón, para ello vamos a modificar las condiciones iniciales de partida de la bola y del pistón del siguiente modo:

En el apartado anterior, la bola chocaba con el pistón en el instante t₁ y su velocidad antes del choque era u₁. La posición del pistón era

y_p=A·sin(ωt₁).

En este apartado, establecemos la velocidad u₁ y la fase φ=ωt₁ como datos de partida, en el instante t=0

• Movimiento del pistón

El pistón describe un MAS de amplitud A y frecuencia angular ω. Su posición y velocidad en función del tiempo t es

y_p=A·sin(ωt+φ)
v_p= A·ω·cos(ωt+φ)

siendo φ la fase inicial del movimiento

• Movimiento de la bola



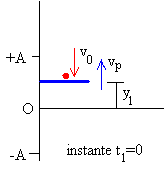
La bola choca con velocidad -v₀ (hacia abajo) en el instante t₁=0 con el pistón en la posición y₁=A·sin(φ). La velocidad de la bola después del choque es

v₁=(1+e)·A·ω·cos(φ)+e·v₀

Después del choque

La posición y la velocidad de la bola en el intervalo t₁<t<t₂ serán

y_b=y₁+v₁(t-t₁)-g(t-t₁)²/2
v_b=v₁-g(t-t₁)

El resto del cálculo es el mismo que en el apartado "Ecuaciones del movimiento"

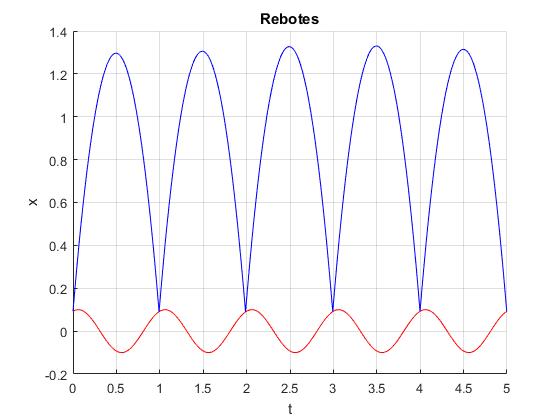
Elaboramos un script de MATLAB para realizar los cálculos y la representación gráfica

A=0.1; %amplitud
w=2*pi; %frecuencia angular, 
phi=68*pi/180; 
v0=4.9; %velocidad inicial
e=0.9; %coeficiente de restitución
%primer choque
v1=(1+e)*A*w*cos(phi)+e*v0;
y1=A*sin(phi);
v0=v1; y0=y1;
t0=0;
hold on
for i=1:5
    y=@(t) y0+v0*(t-t0)-4.9*(t-t0).^2;
    x=@(t) A*sin(w*t+phi);
    T1=t0+v0/9.8; %tiempo que tarda en alcanza la altura máxima
    T2=t0+(v0+sqrt(v0^2-4*4.9*(-A-y0)))/9.8; % en llegar a y=-A
    z=@(t) y(t)-x(t);
    t1=fzero(z,[T1,T2]); %tiempo de choque
    fplot(x,[t0,t1],'color','r');
    fplot(y,[t0,t1],'color','b');
    v1=(1+e)*A*w*cos(w*t1+phi)-e*(v0-9.8*(t1-t0));
    t0=t1;
    v0=v1;
    y0=y(t1);
end
hold off
grid on
xlabel('t')
ylabel('x')
title('Rebotes')

Actividades

Se introduce

• El coeficiente de restitución e, actuando en la barra de desplazamiento titulada Coef. restitución.

• La frecuencia angular ω del M.A.S. que describe el pistón en rad/s, en el control de edición titulado Frecuencia.

• La fase inicial φ, en grados, en el control de edición titulado Fase

• La amplitud de dicho MAS se ha fijado en A=0.1 m=10 cm

• La velocidad inicial v₀ (hacia abajo) en m/s, en el control de edición titulado Velocidad

Se pulsa el botón Nuevo.

Se observa el movimiento de caída de la bola y los sucesivos rebotes sobre el pistón. En la parte derecha, se representa la posición de la bola y del pistón en función del tiempo t.

Se sugiere al lector que experimente con el programa interactivo, cambiando la fase para valores fijos de la velocidad inicial, de la frecuencia y del coeficiente de restitución. Se cambia ligeramente el coeficiente de restitución, manteniendo fijos los otros parámetros y así, sucesivamente.

Referencias

Alvarez, Luis W., Senecal G. Mechanical analog of the synchrotron, illustrating phase stability and two-dimensional focusing. Am. J. Phys. 43 (4) April 1972, pp. 293-296

Tufillaro N. B., Mello T. M., Choi Y. M. Albano A. M. Period doubling of a bouncing ball, J. Physique 47 Septembre (1986) pp. 1477-1482