Oscilador forzado no lineal
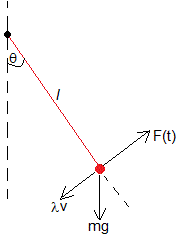
El péndulo consiste en una varilla rígida de longitud l y de masa despreciable que puede girar alrededor de un eje que pasa por uno de sus extremos, unida a una partícula de masa m situada en el otro extremo. Sobre la partícula actúa una fuerza F(t) y una fuerza de rozamiento proporcional a la velocidad v en los sentidos indicados en la figura. La ecuación de la dinámica de rotación alrededor del eje fijo es
ml2 es el momento de inercia del sistema formado por la varilla y la partícula, respecto del eje de rotación perpendicular a la varilla. v=l·dθ/dt es la velocidad de la partícula
En la miembro derecho, tenemos los momentos respecto de dicho eje de las fuerzas que actúan sobre la partícula.
Supondremos que F(t)=F0cos(ωft), donde F0 es la amplitud y ωf es la frecuencia de la fuerza oscilante
El parámetro f=F0/(mg) es el cociente entre la amplitud de la fuerza oscilante y el peso de la partícula.
Cuando el desplazamiento angular es pequeño, sinθ≈θ, la ecuación es lineal y su solución es
Ejemplo
- Frecuencia de la fuerza oscilante, ωf=2π
- Frecuencia natural es ω0=1.5ωf
- Coeficiente de amortiguamiento, γ=ω0/4
- Coeficiente de la fuerza f=0.2
Resolvemos la ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales: en el instante t=0, θ=0, dθ/dt=0
Comparamos la solución numérica con la analítica aproximada
wf=1; %frecuencia de la fuerza oscilante
w0=1.5*wf; %frecuencia natural
gamma=w0/4; %amortiguamiento
f=0.2; %fuerza oscilante
func=@(t,x) [x(2); -2*gamma*x(2)-w0^2*sin(x(1))+f*w0^2*cos(wf*t)];
[t,x]=ode45(func,[0,10*2*pi/wf],[0,0]);
w=sqrt(w0^2-gamma^2);
xx=@(t) f*w0^2*((w0^2-wf^2)*(cos(wf*t)-exp(-gamma*t).*cos(w*t))+
2*gamma*wf*(sin(wf*t)-(w0^2+wf^2)*exp(-gamma*t).*sin(w*t)/(2*w*wf)))
/((w0^2-wf^2)^2+4*gamma^2*wf^2);
hold on
plot(t, x(:,1))
fplot(xx,[0,10*2*pi/wf])
hold off
grid on
xlabel('t')
ylabel('\theta')
title('Oscilaciones forzadas')
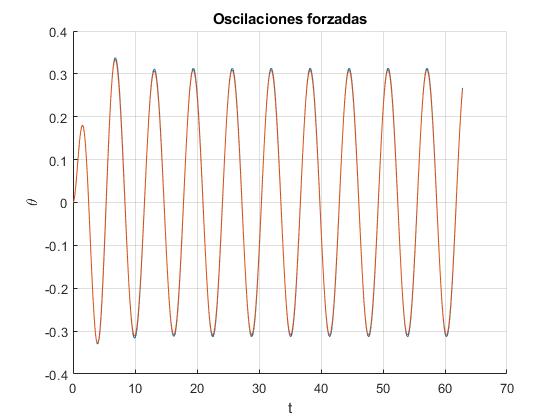
La solución analítica aproximada coincide con la solución obtenida mediante el procedimiento numérico
Comportamiento no lineal
En la página titulada El péndulo doble ya estudiamos un sistema no lineal cuyo comportamiento es complejo comparado con el sistema lineal, cuando los desplazamientos angulares son pequeños
En esta página, vamos a examinar el comportamiento del sistema descrito por la ecuación diferencial
Se ha cambiado cos(ωft) por sin(ωft), para reproducir algunas de las figuras del artículo mencionado en las referencias
Ejemplos
Mediante estos ejemplos, podemos vislumbrar la complejidad de la descripción de este sistema mecánico simple
Ejemplo 1
- Frecuencia natural, ω0=1
- Frecuencia de la fuerza oscilante, ωf=0.01·ω0
- Coeficiente de amortiguamiento, γ=ω0/(2·10)
- Amplitud de la fuerza oscilante, φ0=57.2958°
Resolvemos la ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales: en el instante t=0, θ=0.0558°, dθ/dt=0.01 rad/s
Representamos el desplazamiento angular θ en función del tiempo t durante tres periodos 3·(2π/ωf)
w0=1; %frecuencia natural
wf=0.01*w0; %frecuencia de la fuerza oscilante
gamma=w0/(2*10); %amortiguamiento
f0=57.2958*pi/180;
func=@(t,x) [x(2); -2*gamma*x(2)-w0^2*sin(x(1))+f0*w0^2*sin(wf*t)];
[t,x]=ode45(func,[0,3*2*pi/wf],[0.0558*pi/180,0.01]);
plot(t, x(:,1))
grid on
xlabel('t')
ylabel('\theta')
title('Oscilaciones forzadas')
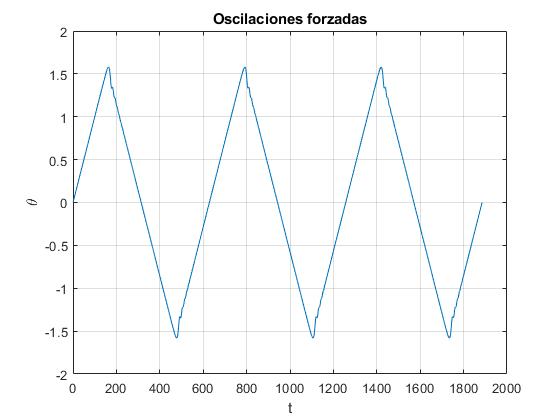
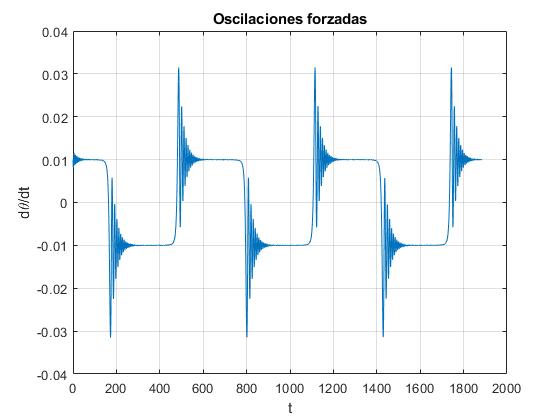
Representamos la velocidad angular dθ/dt en función del tiempo t
w0=1; %frecuencia natural
wf=0.01*w0; %frecuencia de la fuerza oscilante
gamma=w0/(2*10); %amortiguamiento
f0=57.298*pi/180;
func=@(t,x) [x(2); -2*gamma*x(2)-w0^2*sin(x(1))+f0*w0^2*sin(wf*t)];
[t,x]=ode45(func,[0,3*2*pi/wf],[0.0558*pi/180,0.01]);
plot(t, x(:,2))
grid on
xlabel('t')
ylabel('d\theta/dt')
title('Oscilaciones forzadas')
Ejemplo 2
Incrementamos la frecuencia angular de la fuerza oscilante
- Frecuencia natural, ω0=1
- Frecuencia de la fuerza oscilante, ωf=0.03·ω0
- Coeficiente de amortiguamiento, γ=ω0/(2·3.5)
- Amplitud de la fuerza oscilante, φ0=57.8°
Resolvemos la ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales: en el instante t=0, θ=-29.5°, dθ/dt=-0.343 rad/s
Representamos el desplazamiento angular θ en función del tiempo t durante tres periodos 3·(2π/ωf)
w0=1; %frecuencia natural
wf=0.03*w0; %frecuencia de la fuerza oscilante
gamma=w0/(2*3.5); %amortiguamiento
f0=57.8*pi/180;
func=@(t,x) [x(2); -2*gamma*x(2)-w0^2*sin(x(1))+f0*w0^2*sin(wf*t)];
[t,x]=ode45(func,[0,3*2*pi/wf],[-29.5*pi/180,-0.343]);
plot(t, x(:,1))
grid on
xlabel('t')
ylabel('\theta')
title('Oscilaciones forzadas')
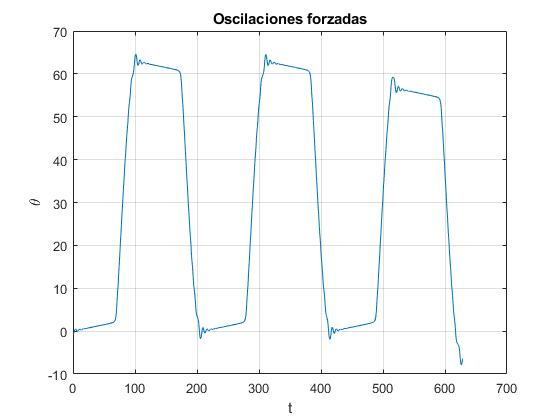
Representamos la velocidad angular dθ/dt en función del tiempo t
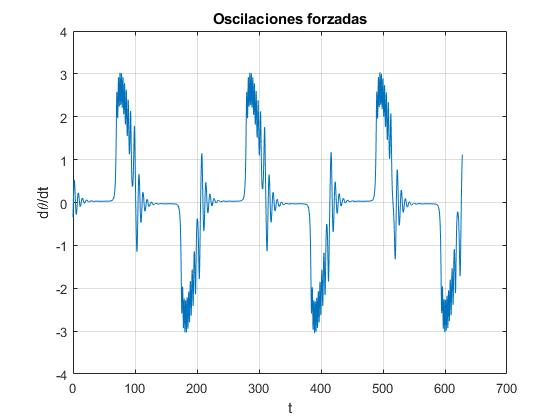
Ejemplo 3
- Frecuencia natural, ω0=1
- Frecuencia de la fuerza oscilante, ωf=0.75·ω0
- Coeficiente de amortiguamiento, γ=ω0/(2·10)
- Amplitud de la fuerza oscilante, φ0=12.5°
Resolvemos la ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales: en el instante t=0, θ=-101.1°, dθ/dt=-0.92 rad/s
Representamos el desplazamiento angular θ en función del tiempo t durante tres periodos 3·(2π/ωf)
w0=1; %frecuencia natural
wf=0.75*w0; %frecuencia de la fuerza oscilante
gamma=w0/(2*10); %amortiguamiento
f0=12.5*pi/180;
func=@(t,x) [x(2); -2*gamma*x(2)-w0^2*sin(x(1))+f0*w0^2*sin(wf*t)];
[t,x]=ode45(func,[0,3*2*pi/wf],[-101.1*pi/180,-0.92]);
plot(t, x(:,1))
grid on
xlabel('t')
ylabel('\theta')
title('Oscilaciones forzadas')
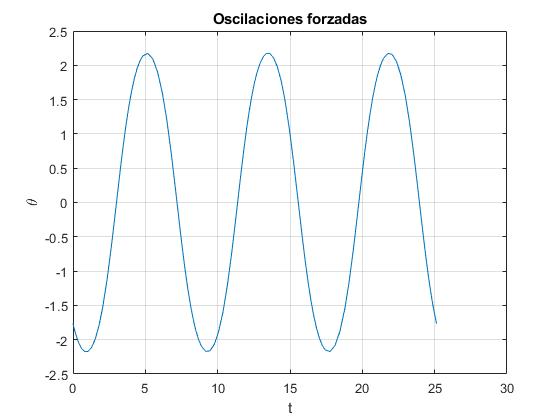
Representamos la velocidad angular dθ/dt en función del tiempo t
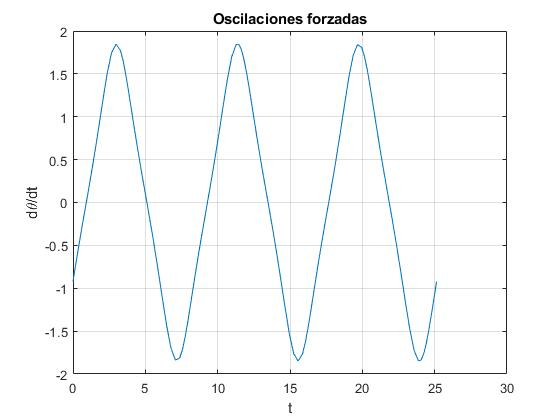
Ejemplo 4
- Frecuencia natural, ω0=1
- Frecuencia de la fuerza oscilante, ωf=0.442·ω0
- Coeficiente de amortiguamiento, γ=ω0/(2·30)
- Amplitud de la fuerza oscilante, φ0=4°
Resolvemos la ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales: en el instante t=0, θ=-147.0°, dθ/dt=-0.555 rad/s
Representamos el desplazamiento angular θ en función del tiempo t durante tres periodos 3·(2π/ωf)
w0=1; %frecuencia natural
wf=0.442*w0; %frecuencia de la fuerza oscilante
gamma=w0/(2*30); %amortiguamiento
f0=4*pi/180;
func=@(t,x) [x(2); -2*gamma*x(2)-w0^2*sin(x(1))+f0*w0^2*sin(wf*t)];
[t,x]=ode45(func,[0,3*2*pi/wf],[-147*pi/180,-0.555]);
plot(t, x(:,2))
grid on
xlabel('t')
ylabel('d\theta/dt')
title('Oscilaciones forzadas')
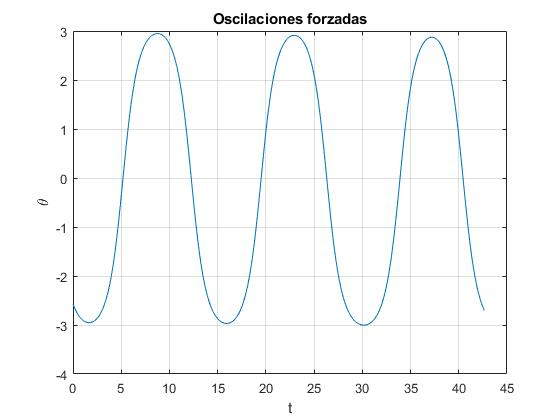
Representamos la velocidad angular dθ/dt en función del tiempo t
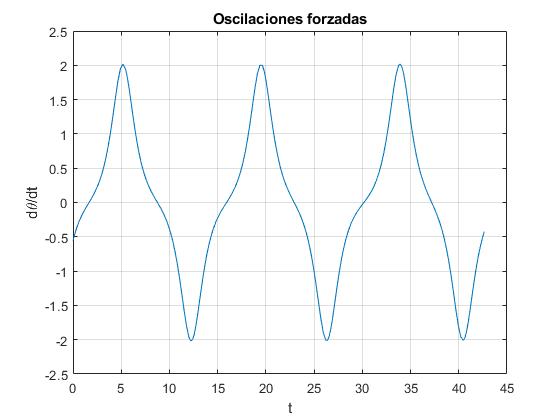
Actividades
Se introduce
- Parámetros del sistema mecánico
- La frecuencia de la fuerza oscilante, en el control titulado Frec. ωf
- La constante de amortiguamiento, en el control titulado Amortig. γ
- La amplitud de la fuerza oscilante (grados), en el control titulado Amplitud φ0
- Se ha fijado el valor de la frecuencia natural, ω0= 1 rad/s
- Condiciones iniciales
- La posición angular inicial (grados), en el control titulado Posición inicial θ0
- La velocidad angular inicial, en el control titulado Velocidad (dθ/dt)0
- Las escalas
- La escala de la representación gráfica del desplazamiento angular θ(t) en color rojo, en el control titulado Escala θ.
- La escala de la representación gráfica de la velocidad angular dθ/dt en color azul, en el control titulado Escala dθ/dt.
- La escala del tiempo t. El tiempo total es n periodos o n·(2π/ωf), un número entero en el control titulado Periodos 2π/ωf
Los controles desplagables nos proporcionan valores predefinidos de las escalas, pero se pueden introducir otros valores.
Podemos elegir
- La representación gráfica de la posición angular θ(t) en color rojo y de la velocidad angular dθ/dt, en color azul
- El movimiento de rotación del péndulo en el panel izquierdo, la trayectoria en el espacio de las fases en el panel derecho: θ en el eje horizontal y dθ/dt en el eje vertical
En la parte superior derecha, se proporcionan los datos de
- El tiempo, t
- la posición angular, θ
- la velocidad angular de rotación, dθ/dt
La flecha de color rojo que actúa sobre la partícula indica la dirección y el sentido de la fuerza F(t)
En la siguiente tabla, se porporcionan los datos de los parámetros del sistema y las condiciones iniciales, de los ejemplos que aparecen en las figuras del artículo citado en las referencias. El lector deberá en cada uno de los casos cambiar las escalas para que la representación gráfica sea visible
| ωf | γ | φ0 (grados) | θ0 (grados) | (dθ/dt)0 | Figuras |
|---|---|---|---|---|---|
| 0.01 | 0.05 | 57.2985 | 0.0558 | 0.01 | 2 y 3 |
| 0.03 | 0.143 | 57.8 | -29.5 | -0.343 | 5 |
| 0.75 | 0.05 | 12.5 | -101.1 | -0.92 | 8 |
| 0.442 | 0.017 | 4 | -147 | -0.555 | 9 y 10 |
| 1.85 | 0.00178 | 35.0 | -3.99 | -2.27 | 12 |
| 2.65 | 0.005 | 26.18 | 142.95 | -0.6272 | 13 |
| 0.26 | 0.02 | 45 | 13.28 | 1.253 | 14 |
| 0.23 | 0.07 | 51 | 7.45 | 1.22 | 15 (a) |
| 0.1483 | 0.0227 | 50.0 | -17.95 | -0.50 | 15 (b) |
| 0.765 | 0.033 | 30 | 43.48 | -2.037 | 16 |
| 0.9 | 0.00083 | 12 | -5.18 | -0.677 | 17 |
| 0.22 | 0.0333 | 45.8 | -63.36 | -4.183 | 19 |
Referencias
Eugene I Butikov. Extraordinary oscillations of an ordinary forced pendulum. Eur. J. Phys. 29 (2008) pp. 215-233. http://butikov.faculty.ifmo.ru/Forced_Pendulum.pdf

