Vamos a emplear el procedimiento de mínimos cuadrados para ajustar un conjunto de datos (t_i,x_i) a la función

x= A₀+A₁cos(ωt)+ B₁sin(ωt)

El criterio de ajuste se toma como aquél en el que la desviación cuadrática media sea mínima, es decir, debe de ser mínima la suma

${\displaystyle \begin{array}{l}S={\displaystyle \sum _{i=1}^N{\left\{x_i-(A_0+A_1\cos (\omega t_i)+B_1\sin (\omega t_i))\right\}}^2}\\ \frac{\partial S}{\partial A_0}=0N·A_0+\left({\displaystyle \sum _{i=1}^N\cos (\omega t_i)}\right)A_1+\left({\displaystyle \sum _{i=1}^N\sin (\omega t_i)}\right)B_1={\displaystyle \sum _{i=1}^N{x}_i}\\ \frac{\partial S}{\partial A_1}=0\left({\displaystyle \sum _{i=1}^N\cos (\omega t_i)}\right)A_0+\left({\displaystyle \sum _{i=1}^N{\cos }^2(\omega t_i)}\right)A_1+\left({\displaystyle \sum _{i=1}^N\sin (\omega t_i)\cos (\omega t_i)}\right)B_1={\displaystyle \sum _{i=1}^N{x}_i\cos (\omega t_i)}\\ \frac{\partial S}{\partial B_1}=0\left({\displaystyle \sum _{i=1}^N\sin (\omega t_i)}\right)A_0+\left({\displaystyle \sum _{i=1}^N\cos (\omega t_i)\sin (\omega t_i)}\right)A_1+\left({\displaystyle \sum _1^N{\sin }^2(\omega t_i)}\right)B_1={\displaystyle \sum _{i=1}^N{x}_i\sin (\omega t_i)}\\ \left(\begin{array}{ccc}N& {\displaystyle \sum _{i=1}^N\cos (\omega t_i)}& {\displaystyle \sum _{i=1}^N\sin (\omega t_i)}\\ \left({\displaystyle \sum _{i=1}^N\cos (\omega t_i)}\right)& \left({\displaystyle \sum _{i=1}^N{\cos }^2(\omega t_i)}\right)& {\displaystyle \sum _{i=1}^N\sin (\omega t_i)\cos (\omega t_i)}\\ {\displaystyle \sum _{i=1}^N\sin (\omega t_i)}& {\displaystyle \sum _{i=1}^N\cos (\omega t_i)\sin (\omega t_i)}& {\displaystyle \sum _{i=1}^N{\sin }^2(\omega t_i)}\end{array}\right)\left(\begin{array}{c}{A}_0\\ A_1\\ B_1\end{array}\right)=\left(\begin{array}{c}{\displaystyle \sum _{i=1}^N{x}_i}\\ {\displaystyle \sum _{i=1}^N{x}_i\cos (\omega t_i)}\\ {\displaystyle \sum _{i=1}^N{x}_i\sin (\omega t_i)}\end{array}\right)\end{array}}$

Resolvemos el sistema de tres ecuaciones con tres incógnitas mediante el operador \ división a la izquierda para obtener el valor de los coeficientes A₀, A₁, B₁.

Ejemplo:

La temperatura media en cada uno de los meses del año en un cierto lugar ha sido la siguiente

El periodo P=12 meses, la frecuencia angular ω=2π/360 rad/dia.

Para crear una tabla (t_i,x_i), asignamos el valor de la temperatura media del mes al día correspondiente a la mitad del mes, suponiendo que todos los meses tengan los mismos días.

t=(1:12)-0.5; 
x=[18.9 21.1 23.3 27.8 32.2 37.2 38.0 36.1 34.4 29.4 23.3 18.9];
w=2*pi/12;

M=[length(t), sum(cos(w*t)), sum(sin(w*t))
sum(cos(w*t)), sum(cos(w*t).^2), sum(sin(w*t).*cos(w*t))
sum(sin(w*t)),sum(sin(w*t).*cos(w*t)), sum(sin(w*t).^2)]

C=[sum(x);sum(x.*cos(w*t));sum(x.*sin(w*t))];
A=M\C

hold on
plot(t,x,'ro','markersize',4,'markerfacecolor','r')
y=@(t) A(1)+A(2)*cos(w*t)+A(3)*sin(w*t);
fplot(y,[t(1),t(end)]);
xlabel('mes')
ylabel('temperatura °C')
title('Ajuste a funciones armónicas')
grid on
hold off

Corremos el script en la ventana de comandos

    M =
   12.0000   -0.0000    0.0000
   -0.0000    6.0000    0.0000
    0.0000    0.0000    6.0000
    A =
   28.3878
   -9.2559
   -2.8002

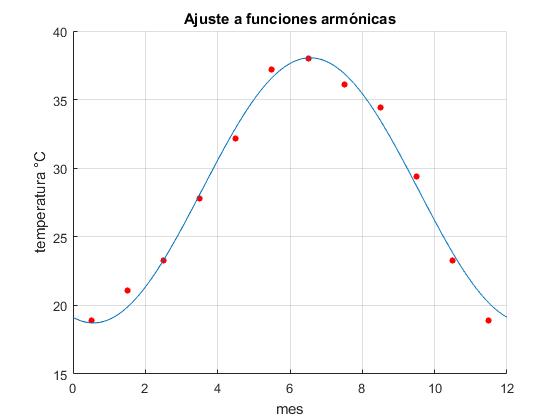
La función que mejor ajusta a los datos es

${\displaystyle x=28.3878-9.2559\cos \left(\frac{\pi }{6}t\right)-2.8002\sin \left(\frac{\pi }{6}t\right)}$

Observamos que los elementos de la matriz de los coeficientes del sistema de tres ecuaciones con tres incógnitas M son nulos excepto los de la diagonal principal. Esto se debe a las propiedades de las funciones armónicas (véase la figura más abajo). Cuando realizamos N=12 observaciones equiespaciadas t_n=n-0.5, n=1,2...N. separadas Δt=P/N, siendo P=12 el periodo, se verifica que

${\displaystyle \begin{array}{l}{\displaystyle \sum _{i=1}^N\sin (\omega t_i)=0}{\displaystyle \sum _{i=1}^N\cos (\omega t_i)=0}\\ \frac{{\displaystyle \sum _{i=1}^N{\sin }^2(\omega t_i)}}{N}=\frac{1}{2}\frac{{\displaystyle \sum _{i=1}^N{\cos }^2(\omega t_i)}}{N}=\frac{1}{2}\\ {\displaystyle \sum _{i=1}^N\sin (\omega t_i)\cos (\omega t_i)=0}\end{array}}$

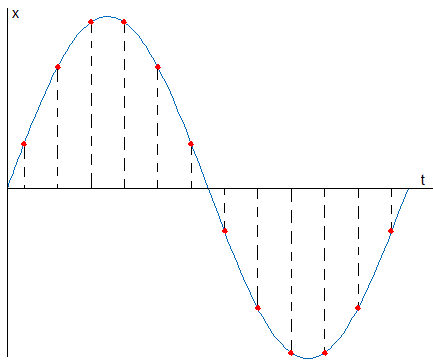
Para demostrarlo, calculamos la suma de la progresión geométrica

${\displaystyle \begin{array}{l}{\displaystyle \sum _{n=1}^{12}\exp \left(i\frac{2\pi }{12}\left(n-\frac{1}{2}\right)\right)}=\exp \left(-i\frac{2\pi }{6}\right){\displaystyle \sum _{n=1}^{12}\exp \left(i\frac{2\pi }{12}n\right)}=\\ \exp \left(-i\frac{2\pi }{6}\right)\frac{1-{\left(\exp \left(i\frac{2\pi }{12}\right)\right)}^{12}}{1-\exp \left(i\frac{2\pi }{12}\right)}=\exp \left(-i\frac{2\pi }{6}\right)\frac{1-\exp \left(2\pi i\right)}{1-\exp \left(i\frac{2\pi }{12}\right)}=0\end{array}}$

>> t=(1:12)-0.5;
>> sum(sin(2*pi*t/12))
ans =  -3.8858e-16
>> sum(cos(2*pi*t/12))
ans =  -6.6613e-16
>> sum(sin(2*pi*t/12).*cos(2*pi*t/12))
ans =  -3.8858e-16

Este resultado se puede generalizar para N medidas igualmente espaciadas en el periodo P

Despejamos los coeficientes A₀, A₁, B₁en el sistema de tres ecuaciones con tres incógnitas

${\displaystyle \begin{array}{l}\left(\begin{array}{ccc}N& 0& 0\\ 0& N/2& 0\\ 0& 0& N/2\end{array}\right)\left(\begin{array}{c}{A}_0\\ A_1\\ B_1\end{array}\right)=\left(\begin{array}{c}{\displaystyle \sum _{i=1}^N{x}_i}\\ {\displaystyle \sum _{i=1}^N{x}_i\cos (\omega t_i)}\\ {\displaystyle \sum _{i=1}^N{x}_i\sin (\omega t_i)}\end{array}\right)\\ A_0=\frac{{\displaystyle \sum _{i=1}^N{x}_i}}{N}\\ A_1=\frac{2}{N}{\displaystyle \sum _{i=1}^N{x}_i\cos (\omega t_i)}{B}_1=\frac{2}{N}{\displaystyle \sum _{i=1}^N{x}_i\sin (\omega t_i)}\end{array}}$

El análisis anterior se puede extender a un modelo general

x= A₀+A₁cos(ωt)+ B₁sin(ωt)+ A₂cos(2ωt)+ B₂sin(2ωt)+...+ A_mcos(mωt)+ B_msin(mωt)

Para datos igualmente espaciados, los coeficientes valen

${\displaystyle \begin{array}{l}{A}_0=\frac{{\displaystyle \sum _{i=1}^N{x}_i}}{N}\\ A_k=\frac{2}{N}{\displaystyle \sum _{i=1}^N{x}_i\cos (k\omega t_i)}{B}_k=\frac{2}{N}{\displaystyle \sum _{i=1}^N{x}_i\sin (k\omega t_i)}k=\mathrm{1,2,...}m\end{array}}$

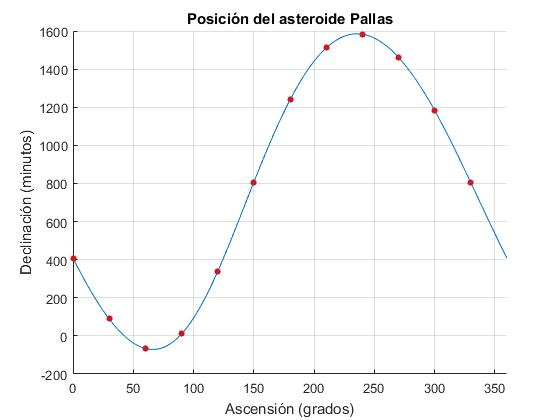
Posición del asteriode Pallas

Gauss estaba interesado en calcular de un modo preciso la órbita del asteroide Pallas, a partir de las observaciones de su posición.

Disponía de 12 pares de datos (x_i,y_i) que deseaba interpolar con seis funciones armónicas.

y= A₀+A₁cos(ωx)+ B₁sin(ωx)+ A₂cos(2ωx)+ B₂sin(2ωx)+...+ A₆cos(6ωx)+ B₆sin(6ωx)

x=0:30:330; 
y=[408 89 -66 10 338 807 1238 1511 1583 1462 1183 804];
hold on
plot(x,y,'ro','markersize',4,'markerfacecolor','r')

n=length(y);
w=2*pi/360;
a0=sum(y)/n;
k=1:6;
a=cos(w*k'*x)*y'*2/n;
b=sin(w*k'*x)*y'*2/n;

x=0:360;
y=a0+a'*cos(w*k'*x)+b'*sin(w*k'*x);
plot(x,y)

xlim([0 360])
xlabel('Ascensión (grados)')
ylabel('Declinación (minutos)')
title('Posición del asteroide Pallas')
grid on
hold off

Ejercicios

Ajustar un conjunto de datos (t_i,x_i) a la función

x= A₀+A₁cos(ωt)+ B₁sin(ωt)

ω=2π/12

ω=2π/1.5