Establecimiento del equilibrio

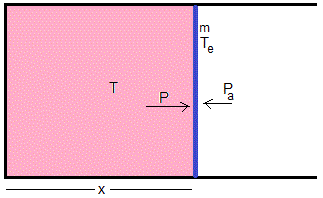
Un cilindro horizontal de sección A contiene un gas ideal a una temperatura inicial T₀ y presión P₀. Un émbolo de masa m que se puede mover sin rozamiento separa el gas de la atmósfera, cuya presión es constante e igual a P_a. Sea x la posición del émbolo en el instante t y x₀ la posición inicial.

El número de moles del gas ideal es

$n = \frac{P_{0} A x_{0}}{R T_{0}}$

donde R=8.3143 J/(K·mol) es la constante de los gases ideales

Cuando se libera el émbolo, debido a la diferencia de presión entre el gas ideal y de la atmósfera, empieza a moverse. Para determinar la posición x del émbolo en función del tiempo t, supondremos que

La presión y temperatura del gas ideal son uniformes en todo el recipiente en cada instante. La temperatura del émbolo T_e es uniforme en cada instante

Cuando la temperatura T del gas es mayor que a temperatura T_e del émbolo, fluye calor desde el gas hacia el émbolo y viceversa. Las paredes del cilindro son aislantes y no hay transferencia de calor entre el émbolo y la atmósfera

Evolución del sistema

Se describe el comportamiento del sistema mediante tres ecuaciones diferenciales y la ecuación de estado del gas ideal

La ecuación del movimiento del émbolo es

$m \frac{d v}{d t} = P A - P_{a} A$

Transferencia de calor entre el émbolo y el gas

La ley de Fourier establece que el flujo de calor (energía por unidad de área y unidad de tiempo) es proporcional al gradiente de temperatura.

Suponiendo que la temperatura T_e del émbolo es mayor que la del gas ideal T. El calor absorbido por el gas ideal es

$\frac{d Q_{g}}{d t} = h A (T_{e} - T)$

donde h es un coeficiente efectivo de transferencia de calor con unidades W/(m²K)

El primer principio para el gas ideal se escribe

$\begin{array}{l} d U = d Q_{g} - P \cdot d V \\ n c_{v} \frac{d T}{d t} = - h A (T - T_{e}) - P A \frac{d x}{d t} \end{array}$

c_v es el calor específico a volumen constante y P es la presión del gas, P·Ax=nRT

La temperatura del émbolo T_e cambia al transferir calor al gas

$\begin{array}{l} \frac{d Q_{e}}{d t} = - h A (T_{e} - T) \\ m c_{e} \frac{d T_{e}}{d t} = h A (T - T_{e}) \end{array}$

donde c_e es el calor específico del émbolo, que supondremos constante

El sistema de tres ecuaciones diferenciales, junto con la ecuación del estado del gas ideal, describen el comportamiento de este sistema. Nos dan la posición del émbolo x, la temperatura del gas T, la presión P del gas y la temperatura T_e del émbolo en función del tiempo t

$\begin{array}{l} {\begin{cases} m \frac{d^{2} x}{d t^{2}} = (P - P_{a}) A \\ n c_{v} \frac{d T}{d t} = - h A (T - T_{e}) - P A \frac{d x}{d t} \\ m c_{e} \frac{d T_{e}}{d t} = h A (T - T_{e}) \end{cases} \\ P (A x) = n R T \end{array}$

Con las condiciones iniciales siguientes: El émbolo parte del reposo desde la posición x₀, la presión inicial del gas es P₀ y las temperaturas del gas y del émbolo son iguales a T₀

Situación final de equilibrio

Al cabo de un tiempo se establecerá un estado final de equilibrio con el émbolo en reposo dx/dt=0 en la posición x_f, las presiones del gas y de la atmósfera serán iguales, P_f=P_a y las temperaturas del gas y del émbolo serán iguales, T_f=T_ef

La energía interna del gas habrá cambiado

$Δ U = n c_{v} (T_{f} - T_{0})$

El trabajo neto de la atmósfera sobre el gas es

$W_{a} = P_{a} A (x_{0} - x_{f})$

El émbolo habrá acumulado calor

$Q_{e} = m c_{e} (T_{f} - T_{0})$

Relacionamos estas tres cantidades. El trabajo de la atmósfera se invierte en cambiar la energía interna del gas ideal y en acumular calor en el émbolo

$- P_{a} A (x_{f} - x_{0}) = n c_{v} (T_{f} - T_{0}) + m c_{e} (T_{f} - T_{0})$

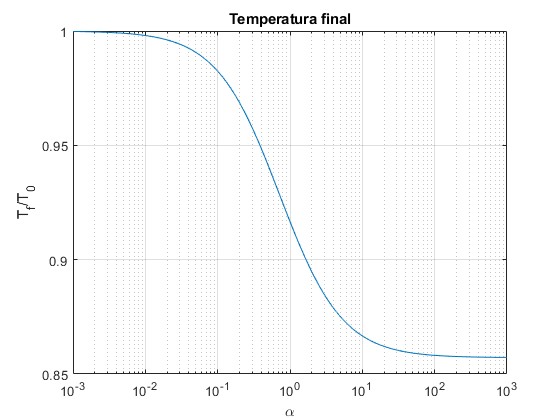
El gas se expande. Si x_f>x₀ entonces T_f<T₀
El gas se comprime. Si x_f<x₀ entonces T_f>T₀

$\begin{array}{l} P_{0} A x_{0} = n R T_{0}, P_{a} A x_{f} = n R T_{f} \\ - P_{a} A (\frac{n R T_{f}}{P_{a} A} - \frac{n R T_{0}}{P_{0} A}) = (n c_{v} + m c_{e}) (T_{f} - T_{0}) \\ \frac{T_{0} P_{a}}{P_{0}} - T_{f} = \frac{n c_{v} + m c_{e}}{n R} (T_{f} - T_{0}) \end{array}$

Relación entre la temperatura inicial T₀ y la final T_f

Definimos el parámetro α y teniendo en cuenta la relación entre los calores específicos molares c_p=c_v+R

$\begin{array}{l} α = \frac{n c_{v}}{m c_{e}} \\ \frac{T_{f}}{T_{0}} = \frac{\frac{P_{a}}{P_{0}} + \frac{n c_{v} + m c_{e}}{n R}}{\frac{n c_{v} + m c_{e}}{n R} + 1} = \frac{\frac{P_{a}}{P_{0}} + \frac{n c_{v} + m c_{e}}{n R}}{\frac{n c_{v} + m c_{e} + n R}{n R}} = \frac{\frac{P_{a}}{P_{0}} + \frac{n c_{v} + m c_{e}}{n R}}{\frac{n c_{p} + m c_{e}}{n R}} = \frac{\frac{1}{n c_{v}} \frac{P_{a}}{P_{0}} + \frac{1}{n R} (1 + \frac{1}{α})}{\frac{1}{n R} (\frac{c_{p}}{c_{v}} + \frac{1}{α})} \\ \frac{T_{f}}{T_{0}} = \frac{\frac{R}{c_{v}} \frac{P_{a}}{P_{0}} + 1 + \frac{1}{α}}{\frac{c_{p}}{c_{v}} + \frac{1}{α}} = \frac{(\frac{c_{p}}{c_{v}} + \frac{1}{α}) + \frac{R}{c_{v}} (\frac{P_{a}}{P_{0}} - 1)}{\frac{c_{p}}{c_{v}} + \frac{1}{α}} \end{array}$

Si P₀>P_a entonces T_f<T₀
Si P₀<P_a entonces T_f>T₀

cualquiera que sea el valor de α (número positivo)

Cuando el parámetro α es pequeño, α→0, o es grande, α→∞

$\begin{array}{l} \lim_{α \to \infty} (1 + \frac{\frac{R}{c_{v}} (\frac{P_{a}}{P_{0}} - 1)}{\frac{c_{p}}{c_{v}} + \frac{1}{α}}) = 1 + \frac{R}{c_{p}} (\frac{P_{a}}{P_{0}} - 1) \\ \lim_{α \to 0} (1 + \frac{\frac{R}{c_{v}} (\frac{P_{a}}{P_{0}} - 1)}{\frac{c_{p}}{c_{v}} + \frac{1}{α}}) = 1 \end{array}$

Ejemplo

Calor específico a volumen constante c_v=5R/2, c_p=7R/2
Presión inicial P₀/P_a=2

Representamos la temperatura final T_f/T₀ en función de α

p0=2; %P0/Pa
cv=2.5; %cv/R
cp=3.5;

%temperatura Tf/T0
T=@(x) (cp/cv+1./x+(1/p0-1)/cv)./(cp/cv+1./x);
x=logspace(-3,3,100);
semilogx(x,T(x))
grid on
xlabel('\alpha')
ylabel('T_f/T_0');
title('Temperatura final')

Relación entre la posición inicial x₀ y la final x_f

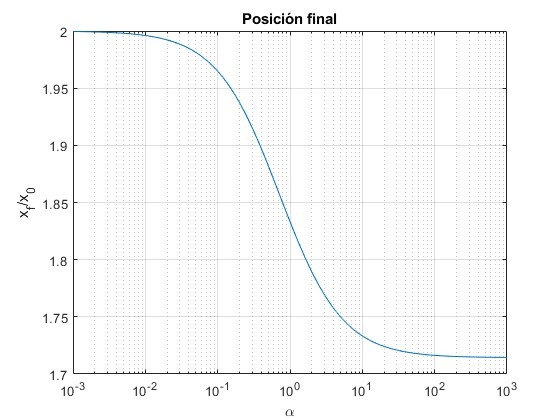
$\begin{array}{l} \frac{x_{f}}{x_{0}} = \frac{P_{0} T_{f}}{P_{a} T_{0}} = \frac{(\frac{c_{p}}{c_{v}} + \frac{1}{α}) \frac{P_{0}}{P_{a}} + \frac{R}{c_{v}} (1 - \frac{P_{0}}{P_{a}})}{\frac{c_{p}}{c_{v}} + \frac{1}{α}} = \frac{\frac{R}{c_{v}} + (\frac{c_{p}}{c_{v}} + \frac{1}{α} - \frac{R}{c_{v}}) \frac{P_{0}}{P_{a}}}{\frac{c_{p}}{c_{v}} + \frac{1}{α}} = \frac{\frac{R}{c_{v}} + (\frac{1}{α} + 1) \frac{P_{0}}{P_{a}}}{\frac{c_{p}}{c_{v}} + \frac{1}{α}} \\ \frac{x_{f}}{x_{0}} = \frac{(\frac{c_{p}}{c_{v}} + \frac{1}{α}) + (\frac{1}{α} + 1) (\frac{P_{0}}{P_{a}} - 1)}{\frac{c_{p}}{c_{v}} + \frac{1}{α}} \end{array}$

x_f=x₀ para P₀=P_a (no hay movimiento del émbolo)
x_f>x₀ para P₀>P_a, el gas se expande
x_f<x₀ para P₀<P_a, el gas se comprime

Cuando el parámetro α es pequeño, α→0, o es grande, α→∞

$\begin{array}{l} \lim_{α \to 0} \underset{α \to 0}{(1 + \frac{(\frac{1}{α} + 1)}{\frac{c_{p}}{c_{v}} + \frac{1}{α}} (\frac{P_{0}}{P_{a}} - 1))} = 1 + \frac{P_{0}}{P_{a}} - 1 = \frac{P_{0}}{P_{a}} \\ \lim_{α \to \infty} \underset{α \to 0}{(1 + \frac{(\frac{1}{α} + 1)}{\frac{c_{p}}{c_{v}} + \frac{1}{α}} (\frac{P_{0}}{P_{a}} - 1))} = 1 + \frac{1}{\frac{c_{p}}{c_{v}}} (\frac{P_{0}}{P_{a}} - 1) = 1 + \frac{c_{v}}{c_{p}} (\frac{P_{0}}{P_{a}} - 1) \end{array}$

Ejemplo

Calor específico a volumen constante c_v=5R/2, c_p=7R/2
Presión inicial P₀/P_a=2

Representamos la posición final x_f/x₀ en función de α

p0=2; %P0/Pa
cv=2.5; %cv/R
cp=3.5;

%posición final xf/x0
xf=@(x) (cp/cv+1./x+(1./x+1)*(p0-1))./(cp/cv+1./x);
x=logspace(-3,3,100);
semilogx(x,xf(x))
grid on
xlabel('\alpha')
ylabel('x_f/x_0');
title('Posición final')

Entropía

Variación de entropía del gas

$\begin{array}{l} d U = d Q - P \cdot d V \\ \frac{d Q}{T} = n c_{v} \frac{d T}{T} + \frac{n R T}{T A x} A d x \\ Δ S_{g} = n c_{v} \int_{T_{0}}^{T_{f}} \frac{d T}{T} + n R \int_{x_{0}}^{x_{f}} \frac{d x}{x} \\ Δ S_{g} = n c_{v} \ln \frac{T_{f}}{T_{0}} + n R \ln \frac{x_{f}}{x_{0}} = n c_{v} \ln \frac{T_{f}}{T_{0}} + n R \ln \frac{P_{0} T_{f}}{P_{f} T_{0}} = n c_{p} \frac{T_{f}}{T_{0}} - n R \ln \frac{P_{a}}{P_{0}} \end{array}$

Variación de entropía del émbolo

$Δ S_{e} = \int_{T_{0}}^{T_{f}} \frac{d Q}{T} = m c_{e} \int_{T_{0}}^{T_{f}} \frac{d T}{T} = m c_{e} \ln \frac{T_{f}}{T_{0}}$

Variación total de entropía

$\begin{array}{l} Δ S = Δ S_{g} + Δ S_{e} = n c_{p} \frac{T_{f}}{T_{0}} - n R \ln \frac{P_{a}}{P_{0}} + m c_{e} \ln \frac{T_{f}}{T_{0}} = (n c_{p} + m c_{e}) \ln \frac{T_{f}}{T_{0}} - n R \ln \frac{P_{a}}{P_{0}} \\ \frac{Δ S}{n R} = (\frac{c_{p}}{R} + \frac{c_{v}}{R} \frac{1}{α}) \ln \frac{T_{f}}{T_{0}} - \ln \frac{P_{a}}{P_{0}} \end{array}$

Solución numérica del sistema de ecuaciones diferenciales

Antes de resolver las ecuaciones, es conveniente expresarlas en términos de magnitudes adimensionales

$\begin{array}{l} t_{c} = \sqrt{\frac{m x_{0}}{P_{a} A}} \\ τ = \frac{t}{t_{c}}, p = \frac{P}{P_{a}}, ξ = \frac{x}{x_{0}}, Γ = \frac{T}{T_{0}}, Γ_{p} = \frac{T_{p}}{T_{0}} \end{array}$

La ecuación de estado

$\begin{array}{l} P A x = n R T \\ p P_{a} A x_{0} ξ = n R Γ T_{0} \\ p P_{a} A x_{0} ξ = P_{0} A x_{0} Γ \\ p ξ = p_{0} Γ \end{array}$

Ecuación del movimiento. Primera ecuación diferencial

$\begin{array}{l} m \frac{d^{2} x}{d t^{2}} = (P - P_{a}) A \\ m \frac{x_{0} d^{2} ξ}{t_{c}^{2} d τ^{2}} = P A - P_{a} A \\ m \frac{P_{a} A}{m x_{0}} x_{0} \frac{d^{2} ξ}{d τ^{2}} = P A - P_{a} A \\ \frac{d^{2} ξ}{d τ^{2}} = p - 1 \end{array}$

Segunda ecuación diferencial

$\begin{array}{l} n c_{v} \frac{d T}{d t} = - h A (T - T_{e}) - P A \frac{d x}{d t} \\ n c_{v} \frac{T_{0} d Γ}{t_{c} d τ} = - h A T_{0} (Γ - Γ_{e}) - p P_{a} A \frac{x_{0} d ξ}{t_{c} d τ} \\ n c_{v} \frac{T_{0} d Γ}{t_{c} d τ} = - h A T_{0} (Γ - Γ_{e}) - p P_{a} A \frac{x_{0} d ξ}{t_{c} d τ} \\ n c_{v} \frac{T_{0} d Γ}{t_{c} d τ} = - h A T_{0} (Γ - Γ_{e}) - p P_{a} \frac{n R T_{0}}{P_{0}} \frac{d ξ}{t_{c} d τ} \\ \frac{d Γ}{d τ} = - \frac{h A}{n c_{v}} t_{c} (Γ - Γ_{e}) - \frac{R}{c_{v}} \frac{p}{p_{0}} \frac{d ξ}{d τ} \\ \frac{d Γ}{d τ} = - \frac{t_{c}}{t_{h}} (Γ - Γ_{e}) - \frac{R}{c_{v}} \frac{p}{p_{0}} \frac{d ξ}{d τ}, t_{h} = \frac{n c_{v}}{h A} \end{array}$

Tercera ecuación diferencial

$\begin{array}{l} m c_{e} \frac{d T_{e}}{d t} = h A (T - T_{e}) \\ m c_{e} \frac{T_{0} d Γ_{e}}{t_{c} d τ} = h A T_{0} (Γ - Γ_{e}) \\ \frac{d Γ_{e}}{d τ} = \frac{h A}{m c_{e}} t_{c} (Γ - Γ_{e}) \\ \frac{d Γ_{e}}{d τ} = \frac{\frac{n c_{v}}{t_{h}}}{\frac{n c_{v}}{α}} t_{c} (Γ - Γ_{e}) \\ \frac{d Γ_{e}}{d τ} = α \frac{t_{c}}{t_{h}} (Γ - Γ_{e}) \end{array}$

Expresamos el sistema de ecuaciones diferenciales en términos de las variables ξ, Γ, Γ_e, utilizando la ecuación de estado pξ=p₀Γ

${\begin{cases} \frac{d^{2} ξ}{d τ^{2}} = \frac{p_{0} Γ}{ξ} - 1 \\ \frac{d Γ}{d τ} = - \frac{t_{c}}{t_{h}} (Γ - Γ_{e}) - \frac{R}{c_{v}} \frac{Γ}{ξ} \frac{d ξ}{d τ} \\ \frac{d Γ_{e}}{d τ} = α \frac{t_{c}}{t_{h}} (Γ - Γ_{e}) \end{cases}$

Dados los valores de c_v/R, α y t_c/t_h, se resuelve el sistema de ecuaciones diferenciales con las condiciones iniciales, τ=0, ξ=1, dξ/dτ=0, (el émbolo inicialmente en reposo) y Γ=Γ_e=1, (la temperatura del gas y del émbolo es la misma) p₀ (presión inicial del gas)

Ejemplo

Presión inicial, p₀=2
Parámetro, α=0.01
Calor específico a volumen constante, c_v/R=5/2, a presión constante c_p/R=7/2

Temperaturas finales del gas y del émbolo

$\frac{T_{f}}{T_{0}} = Γ_{f} = \frac{\frac{c_{p}}{c_{v}} + \frac{1}{α} + \frac{R}{c_{v}} (\frac{1}{p_{0}} - 1)}{\frac{c_{p}}{c_{v}} + \frac{1}{α}} = \frac{\frac{3.5 R}{2.5 R} + \frac{1}{α} + \frac{R}{2.5 R} (\frac{1}{p_{0}} - 1)}{\frac{3.5 R}{2.5 R} + \frac{1}{α}} = 0 .9980$

Posición final

$\frac{x_{f}}{x_{0}} = ξ_{f} = \frac{(\frac{c_{p}}{c_{v}} + \frac{1}{α}) + (\frac{1}{α} + 1) (\frac{P_{0}}{P_{a}} - 1)}{\frac{c_{p}}{c_{v}} + \frac{1}{α}} = \frac{(\frac{3.5 R}{2.5 R} + \frac{1}{α}) + (\frac{1}{α} + 1) (p_{0} - 1)}{\frac{3.5 R}{2.5 R} + \frac{1}{α}} = 1 .9961$

Incremento de entropía

$\begin{array}{l} \frac{Δ S}{n R} = (\frac{c_{p}}{R} + \frac{c_{v}}{R} \frac{1}{α}) \ln \frac{T_{f}}{T_{0}} - \ln \frac{P_{a}}{P_{0}} \\ \frac{Δ S}{n R} = (\frac{3.5 R}{R} + \frac{2.5 R}{R} \frac{1}{0.01}) \ln 0.9980 - \ln \frac{1}{2} = 0 .1856 \end{array}$

El gas se expande y se comprime reversiblemente. La transferencia de calor del gas al émbolo o viceversa, es el único proceso irreversible

Otro dato que precisamos es el cociente t_c/t_h=0.1

Resolvemos el sistema de tres ecuaciones diferenciales mediante el procedimiento ode45 de MATLAB

% x(1) es xi, x(2) es dxi/dtau, x(3) es T (temperatura gas), x(4) es T_e
% (temperatura émbolo)
p0=2;
k1=0.1; %cociente t_c/t_h
cv=2.5; %c_v/R
alfa=0.01;

fg=@(t,x)[x(2); p0*x(3)/x(1)-1; -k1*(x(3)-x(4))-x(3)*x(2)/(cv*x(1));
 alfa*k1*(x(3)-x(4))];
[t,x]=ode45(fg,[0,300],[1,0,1,1]);
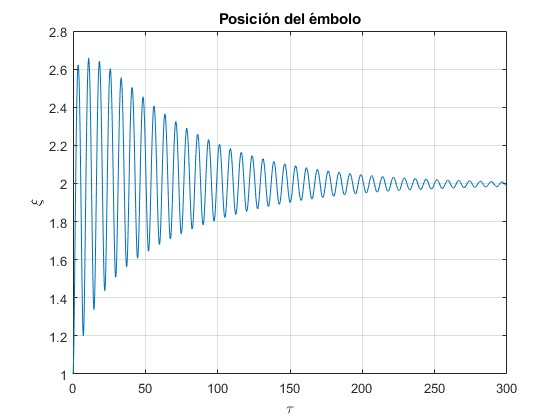
plot(t,x(:,1))
grid on
xlabel('\tau')
ylabel('\xi');
title('Posición del émbolo')

figure
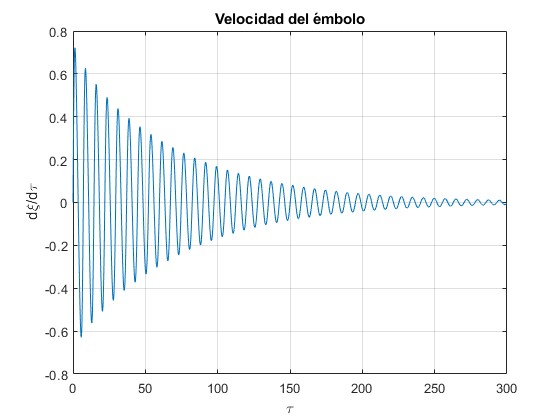
plot(t,x(:,2))
grid on
xlabel('\tau')
ylabel('d\xi/d\tau');
title('Velocidad del émbolo')

figure
hold on
plot(t,x(:,3))
plot(t,x(:,4))
hold off
legend('gas','émbolo','Location', 'best')
grid on
xlabel('\tau')
ylabel('\Gamma');
title('Temperatura del gas y del émbolo')

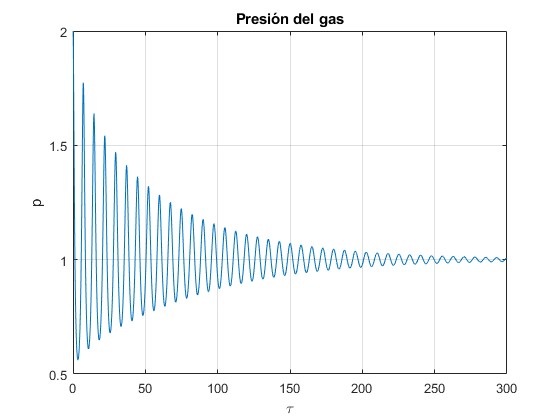
figure
plot(t,p0*x(:,3)./x(:,1))
grid on
xlabel('\tau')
ylabel('p');
title('Presión del gas')

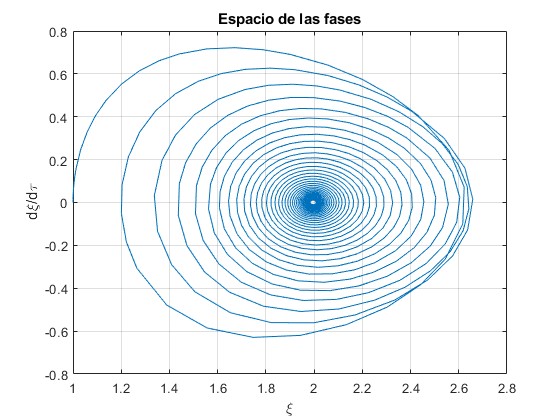
figure
plot(x(:,1),x(:,2))
grid on
xlabel('\xi')
ylabel('d\xi/d\tau');
title('Espacio de las fases')

Posición del émbolo ξ en función del tiempo τ

Velocidad del émbolo dξ/dτ en función del tiempo τ

Velocidad del émbolo dξ/dτ en función de la posición ξ

Presión p del gas en función del tiempo τ

Temperatura del gas Γ y del émbolo Γ_e

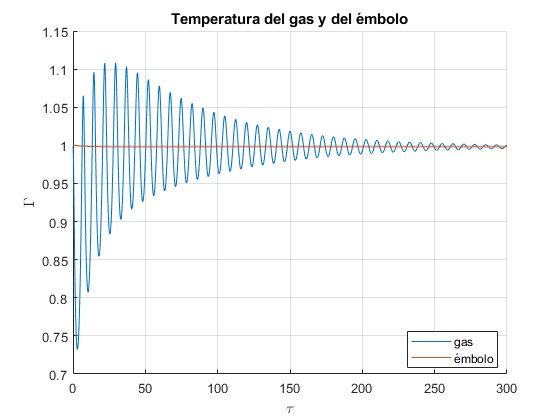
Probar otras situaciones por ejemplo, cambiando el cociente t_c/t_h=1, 10, variable k1 en el código

Investigamos el efecto del cociente t_c/t_h manteniendo fijo el parámero α=0.01.

p0=2;
alfa=0.01; 
cv=2.5; %c_v/R
hold on
for k1=[0.0001, 1,1000] %cociente t_c/t_h
    fg=@(t,x)[x(2); p0*x(3)/x(1)-1; -k1*(x(3)-x(4))-x(3)*x(2)/(cv*x(1)); 
alfa*k1*(x(3)-x(4))];
    [t,x]=ode45(fg,[0,100],[1,0,1,1]);
    plot(x(:,1),x(:,2))
end
hold off
grid on
ylabel('d\xi/d\tau')
legend('0.0001','1','1000','Location', 'southeast')
xlabel('\xi');
title('Espacio de las fases')

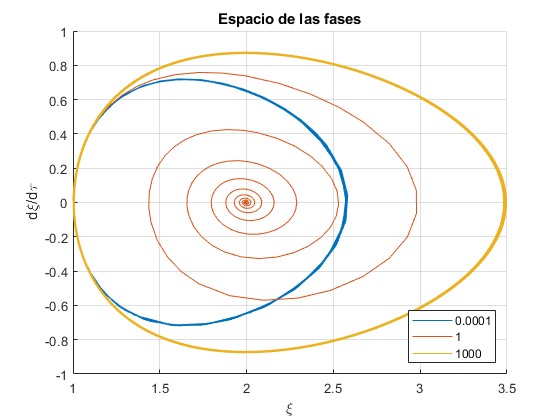
Cuando el cociente t_c/t_h tiende a cero o tiende al infinito, el émbolo oscila, sin alcanzar el estado final de equilibrio

Actividades

Se introduce

Se elige gas ideal, monoatómico c_v=3R/2, diatómico, c_v=5R/2
Presión inicial del gas, p₀ en el control tituladp Presión
El valor del parámetro α en el control tiulado Parámetro
El valor del cociente t_h/t_c en el control tiulado Cociente

Se pulsa el botón titulado Nuevo

Parámetro, α Cociente, t_c/t_h:
Presión inicial, p₀

Referencias

David S. Corti, Joshua A. Ciesar, Juan M. Vazquez. Thermal damping of the motion of a piston: Any irreversibility implies dissipation. Am. J. Phys. 92, pp. 214–220, March 2024