Procesos cuasiestáticos (II)

Proceso de un solo paso

Situación inicial

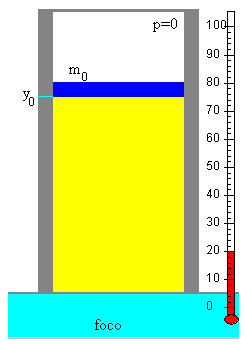
En la situación inicial, el émbolo de masa m₀ está en equilibrio bajo la acción de dos fuerzas:

su peso m₀g
la fuerza que ejerce el la presión p₀ del gas encerado en el recipiente f₀=p₀·S. Siendo S el área del émbolo. m₀g= f₀

Si la altura inicial de equilibrio es y₀. La ecuación de los gases ideales, nos relaciona la presión p₀, el volumen y₀·S y la temperatura T de una masa de gas o de su número n de moles.

p₀·S·y₀ =nRT
f₀·y₀ =nRT

R=8.3143 J/(K·mol) es la constante de los gases

La energía interna inicial del gas ideal es

U₀=nc_vT

Posición de equilibrio

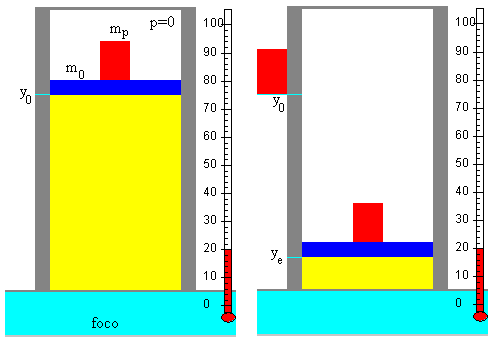
En el instante t=0, se coloca sobre el émbolo un bloque de masa m_p. El émbolo se desequilibra ya que el peso (m₀+m_p)g=mg es mayor que la fuerza que ejerce la presión del gas f₀=p₀·S.

El émbolo se mueve hacia abajo, comprimiendo el gas, hasta que la fuerza f que ejerce el gas sobre el émbolo debido a su presión, se vuelve a igualar al peso mg

En la nueva situación de equilibrio, el peso del conjunto formado por émbolo y el bloque mg se hace igual a la fuerza que ejerce la presión del gas f_e=p_e·S.

mg= f_e

Se calcula esta posición a partir de la ecuación de la transformación isotérmica

$\begin{array}{l} p_{0} V_{0} = p_{e} V_{e} m_{0} y_{0} = m y_{e} \\ y_{e} = \frac{m_{0}}{m_{0} + m_{p}} y_{0} \end{array}$

El movimiento del conjunto bloque-émbolo prosigue, hasta que su velocidad se hace cero y el gas se comprime al máximo. En esta posición el émbolo y el bloque no están en equilibrio.

Ecuación del movimiento

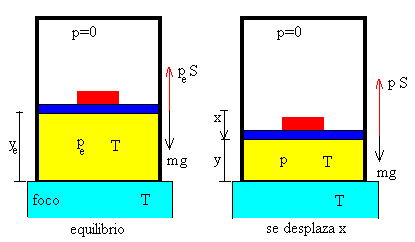
Supongamos que el émbolo y el bloque están en la posición y_e de equilibrio estable. Si se desplaza x de dicha posición. La fuerza que ejerce el gas sobre el émbolo f tiende a restaurar al conjunto émbolo-bloque a la posición de equilibrio.

Las fuerzas sobre el conjunto de los dos cuerpos, cuando se encuentra en la posición y=y_e-x, son

el peso mg
la fuerza que ejerce el la presión p del gas encerado en el recipiente f=p·S.

La segunda ley de Newton se escribe

$m \frac{d^{2} x}{d t^{2}} = m g - f$

Calcaulamos la fuerza f a partir de la transformación isotérmica

$\begin{array}{l} p_{e} V_{e} = p V m g y_{e} = f y \\ \frac{d^{2} x}{d t^{2}} = - g \frac{x}{y_{e} - x} y_{e} = y_{0} (\frac{m_{0}}{m}) \end{array}$

Si x<<y_e

$\frac{d^{2} x}{d t^{2}} + \frac{g}{y_{e}} x = 0$

que es la ecuación diferencial de un MAS de frecuencia angular ω²=g/y_e

El émbolo llega a la posición de equilibrio estable y=y_e después de cierto tiempo, con velocidad v=0. En esta posición de equilibrio, la fuerza f que ejerce el gas sobre el émbolo debida a la presión se anula con el peso del conjunto formado por el bloque y el émbolo f=mg.

Variación de entropía

Como la energía interna del gas solamente depende de la temperatura y ésta es constante. La energía potencial del conjunto émbolo-bloque correspondiente a la altura (y₀-y_e) fluye en forma de calor hacia el foco.

ΔE_p=(m₀+m_p)g(y₀-y_e)

La variación de entropía del foco es

$Δ S_{f} = \frac{(m_{0} + m_{p}) g (y_{0} - y_{e})}{T} = \frac{m_{p} g y_{0}}{T}$

La variación de entropía del gas que cambia su volumen de V₀=y₀·S a V_e=y_e·S es

$Δ S_{g} = n R \ln (\frac{y_{e}}{y_{0}}) = n R \ln (\frac{m_{0}}{m_{0} + m_{p}})$

La variación de entropía total es

ΔS=ΔS_f+ΔS_g>0

Proceso de N pasos

Dividimos el bloque de masa m_p en varios trozos iguales, que se colocan sucesivamente sobre el émbolo cada vez que se alcanza el equilibrio. Nos aproximaremos al proceso reversible a través de una sucesión de estados de equilibrio que nos conducirán desde el estado inicial al final.

Dividimos el bloque en N trozos iguales de masa Δm=m_p/N, donde m_p es la masa del bloque y los vamos colocando sobre el émbolo del siguiente modo:

Situación inicial

Partimos de la situación inicial de equilibrio, con el émbolo a una altura y₀. La fuerza que ejerce el gas f₀ sobre el émbolo debida a la presión se compensa con el peso del émbolo m₀g.

m₀g·y₀ =nRT

Primera etapa

Colocamos un trozo del bloque de masa Δm, observamos que comprime el gas y alcanza la posición de equilibrio y₁. La fuerza f₁ que ejerce el gas debido a la presión, se iguala al peso del conjunto formado por el émbolo y la porción del bloque, f₁=(m₀+ Δm)g. La transformación isoterma

$\begin{array}{l} m_{0} g y_{0} = f_{1} y_{1} \\ y_{1} = \frac{m_{0} y_{0}}{m_{0} + Δ m} \end{array}$

La energía potencial del conjunto émbolo-bloque correspondiente a la altura (y₀-y₁) fluye en forma de calor hacia el foco.

ΔE_p=(m₀+Δm)g(y₀-y₁)

La variación de entropía del foco es

$Δ S_{f} = \frac{(m_{0} + Δ m) g (y_{0} - y_{1})}{T} = \frac{Δ m g y_{0}}{T}$

La variación de entropía del gas que cambia su volumen de V₀=y₀·S a V₁=y₁·S es

$Δ S_{g} = n R \ln (\frac{y_{1}}{y_{0}}) = n R \ln (\frac{m_{0}}{m_{0} + Δ m})$

Segunda etapa

La posición de equilibrio y₁ es ahora la posición inicial cuando se coloca el segundo trozo del bloque de igual masa Δm. Observamos que se comprime el gas y alcanza la posición de equilibrio y₂ a la altura.

$y_{2} = \frac{(m_{0} + Δ m) y_{1}}{m_{0} + 2 Δ m} = \frac{m_{0} y_{0}}{m_{0} + 2 Δ m}$

La energía potencial del conjunto émbolo-bloque correspondiente a la altura (y₁-y₂) fluye en forma de calor hacia el foco.

ΔE_p=(m₀+2Δm)g(y₁-y₂)

La variación de entropía del foco es

$Δ S_{f} = \frac{(m_{0} + 2 Δ m) g (y_{1} - y_{2})}{T} = \frac{Δ m g y_{1}}{T} = \frac{Δ m g}{T} \frac{m_{0} y_{0}}{m_{0} + Δ m}$

La variación de entropía del gas que cambia su volumen de V₁=y₁·S a V₂=y₂·S es

$Δ S_{g} = n R \ln (\frac{y_{2}}{y_{1}}) = n R \ln (\frac{m_{0} + Δ m}{m_{0} + 2 Δ m})$

Etapa N

La posición de equilibrio y_N-1 es la posición inicial cuando se coloca la última porción N de bloque. Observamos que se comprime el gas y alcanza la posición de equilibrio final y_N a la altura.

$y_{N} = \frac{m_{0} y_{0}}{m_{0} + N \cdot Δ m}$

La energía potencial del conjunto émbolo-bloque correspondiente a la altura (y_N-1-y_N) fluye en forma de calor hacia el foco.

ΔE_p=(m₀+NΔm)g(y_N-1-y_N)

La variación de entropía del foco es

$Δ S_{f} = \frac{(m_{0} + N Δ m) g (y_{N - 1} - y_{N})}{T} = \frac{Δ m g y_{N - 1}}{T} = \frac{Δ m g}{T} \frac{m_{0} y_{0}}{m_{0} + (N - 1) Δ m}$

La variación de entropía del gas que cambia su volumen de V_N-1=y_N-1·S a V_N=y_N·S es

$Δ S_{g} = n R \ln (\frac{y_{N}}{y_{N - 1}}) = n R \ln (\frac{m_{0} + (N - 1) Δ m}{m_{0} + N \cdot Δ m})$

Variación de entropía

La variación total de entropía del gas en el proceso isotérmico que lleva al gas desde un volumen V₀ a un volumen V_N es

$\begin{array}{l} Δ S_{g} = n R \ln (\frac{m_{0}}{m_{0} + Δ m}) + n R \ln (\frac{m_{0} + Δ m}{m_{0} + 2 \cdot Δ m}) + .... + n R \ln (\frac{m_{0} + (N - 1) Δ m}{m_{0} + N \cdot Δ m}) = \\ n R \ln (\frac{m_{0}}{m_{0} + N \cdot Δ m}) \end{array}$

La variación de entropía del foco en el mismo proceso es

$\begin{array}{l} Δ S_{f} = \frac{Δ m g}{T} y_{0} (1 + \frac{m_{0}}{m_{0} + Δ m} + \frac{m_{0}}{m_{0} + 2 Δ m} + ... + \frac{m_{0}}{m_{0} + (N - 1) Δ m}) = \\ n R (\frac{Δ m}{m_{0}} + \frac{Δ m}{m_{0} + Δ m} + \frac{Δ m}{m_{0} + 2 Δ m} + ... + \frac{Δ m}{m_{0} + (N - 1) Δ m}) \end{array}$

La variación de entropía total es

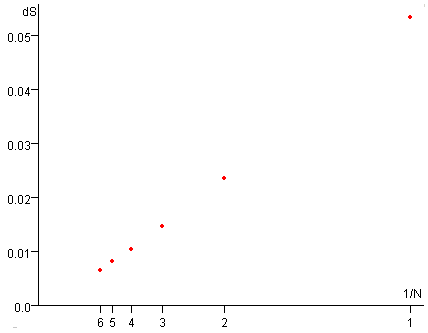
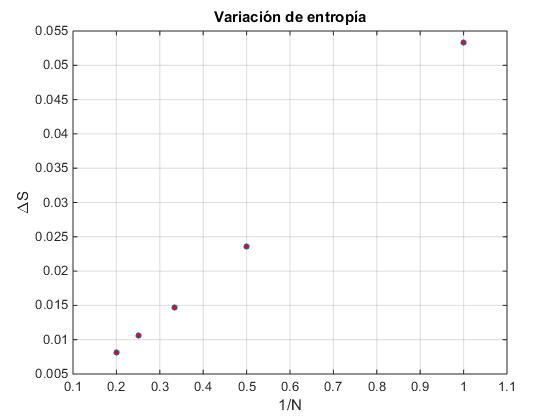
$Δ S = n R \ln (\frac{m_{0}}{m_{0} + N \cdot Δ m}) + n R \sum_{i = 0}^{N - 1} \frac{Δ m}{m_{0} + i \cdot Δ m}$

En la figura se representa:

En el eje vertical la variación de entropía ΔS
En el eje horizontal la inversa 1/N del número de pasos

Cuando el número N de pasos es muy grande la suma de las variaciones de entropía del foco y del gas tiende a cero. ΔS_f+ΔS_g→0

Ejemplo

La masa del émbolo, m₀=1.0 kg.
La masa del bloque, m_p=5.0 kg
El número de moles, n=0.002 mol
Se introduce la temperatura, 20ºC, T=293 K

Proceso de N=1 etapas

Situación inicial

La presión del gas es igual p₀=m₀g/S Aplicando la ecuación de los gases perfectos, conociendo el número n=0.002 de moles y la temperatura T₀=293 K calculamos el volumen o la posición inicial y₀ del émbolo.

$\begin{array}{l} p_{0} V_{0} = n R T_{0} \\ \frac{m_{0} g}{S} \cdot S y_{0} = n R T_{0} y_{0} = \frac{0.002 \cdot 8.3143 \cdot 293}{1 \cdot 9.8} = 0.497 m = 49 .7 cm \end{array}$

Situación final

Se coloca sobre el émbolo un bloque de masa m_p=5.0 kg

Como el gas está en contacto térmico con un foco de calor a temperatura T=293 K, el proceso es isotérmico

m₀gy₀=(m₀+m_p)gy₁

y₁=0.083 m=8.3 cm

La variación de entropía del foco y del gas es

$Δ S = 0.002 \cdot 8.3143 (\ln (\frac{1.0}{1.0 + 5.0}) + \frac{5}{1}) = 0.0533 J/K$

Consideremos ahora un proceso de N=5 etapas,

Los cinco bloques que se colocan sucesivamente sobre el émbolo tienen una masa Δm=m_p/5= 1kg cada uno.

Situación inicial

El émbolo está a una altura y₀=49.7 cm

Primera etapa, se coloca un bloque de Δm=1 kg

La posición final de equilibrio es

m₀gy₀=(m₀+Δm)gy₁

y₁=y₀/2=0.248=24.8 cm

Segunda etapa, se coloca un bloque de Δm=1 kg

m₀gy₀=(m₀+2Δm)gy₂

y₂=y₀/3=0.166 =16.6 cm

Tercera etapa, se coloca un bloque de Δm=1 kg

m₀gy₀=(m₀+3Δm)gy₃

y₃=y₀/4=0.124 =12.4 cm

Cuarta etapa, se coloca un bloque de Δm=1 kg

m₀gy₀=(m₀+4Δm)gy₄

y₄=y₀/5=0.094 =9.9 cm

Quinta etapa, se coloca un bloque de Δm=1 kg

m₀gy₀=(m₀+5Δm)gy₅

y₅=y₀/6=0.083 =8.3 cm

La variación de energía potencial fluye en forma de calor al foco

ΔE_p=(m₀+Δm)g(y₀-y₁)+(m₀+2Δm)g(y₁-y₂)+(m₀+3Δm)g(y₂-y₃)+ (m₀+4Δm)g(y₃-y₄)+ (m₀+5Δm)g(y₄-y₅)=11.12

La variación de entropía del foco es

ΔS_f= ΔE_p/T=0.0380

El gas cambia de volumen. El volumen inicial es V_i=y₀·S y el volumen final es V_f=y₅·S. La variación de entropía es

$Δ S_{g} = n R \ln (\frac{y_{5}}{y_{0}}) = 0.002 \cdot 8.3143 \cdot \ln (\frac{0.083}{0.497}) = - 0.0298$

La variación de entropía total en este proceso es

ΔS= ΔS_f+ΔS_g=0.0082 J/K

Calculamos la variación de entropía mediante la fórmula deducida al final del apartado anterior

$\begin{array}{l} Δ S = 0.002 \cdot 8.3143 (\ln (\frac{1}{1 + 5 \cdot 1}) + \frac{1}{1} + \frac{1}{1 + 1 \cdot 1} + \frac{1}{1 + 2 \cdot 1} + \frac{1}{1 + 3 \cdot 1} + + \frac{1}{1 + 4 \cdot 1}) = \\ 0.0082 J/K \end{array}$

Elaboramos un script para representar:

En el eje vertical la variación de entropía ΔS
En el eje horizontal la inversa 1/N del número de pasos

nMoles=0.002; %moles de gas
m0=1; %masa del émbolo
mp=5; %masa del bloque en trozos completo
N=5; %número de trozos en lo que se divide el bloque
y=zeros(N+1,1);
S=zeros(N+1,1);
SS=zeros(N+1,1);
%situación inicial
T0=293; %temperatura constante del foco
y(1)=nMoles*8.3143*T0/(m0*9.8); %altura de equilibrio inicial
S(1)=0;
%estado de equilibrio al final de cada etapa
for k=1:N
    dm=mp/k; %masa de cada trozo
    for j=1:k
        y(j+1)=y(1)*m0/(m0+j*dm);
        S(j+1)=S(j)+(m0+j*dm)*9.8*(y(j)-y(j+1))/T0
+nMoles*8.3143*log(y(j+1)/y(j));
    end
    SS(k)=S(k+1); %variación de entropía total del proceso de k etapas
end
x=1./(1:N);
plot(x,SS(1:N),'o','markersize',4,'markerfacecolor','r')
xlim([0.1,1.1]) 
grid on
hold off
ylabel('\DeltaS')
xlabel('1/N')
title('Variación de entropía')

Actividades

Se introduce

La temperatura inicial T del foco en contacto con el gas, en el control titulado Temperatura
La masa del émbolo se ha fijado en m₀=1.0 kg.
La masa del bloque se ha fijado en m_p=5.0 kg.
El número de moles se ha fijado en n=0.002 mol

Se pulsa el botón titulado Nuevo.

Se observa la situación inicial de equilibrio, cuando el émbolo está a una altura y₀.

Se pulsa el botón titulado ►

Se pone el bloque sobre el émbolo y observamos su movimiento, hasta que alcanza el estado final de equilibrio

Cuando el émbolo ha alcanzado la posición final de equilibrio, se pulsa el botón titulado >>,

Se observa la situación inicial de equilibrio, cuando el émbolo está a una altura y₀.

Se pulsa el botón titulado ►

El número de pasos es N=2. El proceso consta de una sucesión de dos estados de equilibrio.

Cuando el émbolo ha alcanzado la posición final de equilibrio, se pulsa el botón titulado >>

y así, sucesivamente.

Se representan las fuerzas sobre el conjunto émbolo-bloque,

El peso mg
La fuerza f que ejerce el gas sobre el émbolo debida a la presión

El proceso es una sucesión de N estados de equilibrio. Cuando N es grande, observamos que hay muy poca diferencia en las dos fuerzas que actúan sobre el émbolo a lo largo de todo el proceso. Naturalmente, en las posiciones de equilibrio son iguales.

En la parte derecha, se representa

En el eje vertical la variación de entropía ΔS
En el eje horizontal la inversa 1/N del número de pasos

Cuando el número N de pasos es muy grande la suma de las variaciones de entropía del foco y del gas tiende a cero.

Temperatura:

Referencias

Gupta V. K., Shander G., Sharma N. K. Reversibility and step processes: An experiment for the undergraduate laboratory. Am. J. Phys. 52 (10) October 1984, pp. 945-947