Proceso de un solo paso

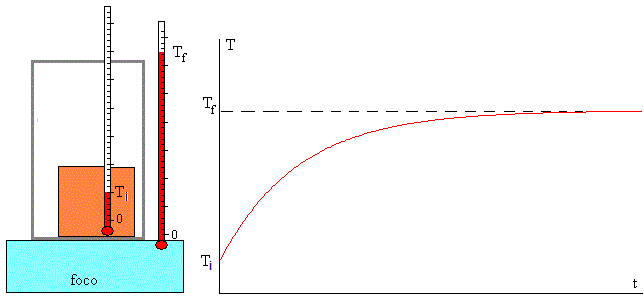
Colocamos un cuerpo de masa m y calor específico c cuya temperatura inicial es T_i en contacto con un foco (ambiente) cuya temperatura es T_f

Como hemos estudiado en la página titulada “Ley del enfriamiento de Newton” al cabo de un cierto tiempo (teóricamente infinito) el cuerpo alcanza la temperatura T_f.

T=T_f+(T_i-T_f)·exp(-k·t)

El cuerpo absorbe una cantidad de calor

Q=m·c·(T_f-T_i)

La variación de entropía del cuerpo es

${\displaystyle \Delta S_c={\displaystyle \underset{T_i}{\overset{T_f}{\int }}\frac{dQ}{T}}=mc{\displaystyle \underset{T_i}{\overset{T_f}{\int }}\frac{dT}{T}}=mc\ln \left(\frac{T_f}{T_i}\right)}$

El foco de calor cede una cantidad de calor Q sin cambiar su temperatura T_f. Su variación de entropía es

${\displaystyle \Delta S_f=\frac{-Q}{T_f}=-mc\frac{T_f-T_i}{T_f}}$

La variación de entropía del sistema formado por el cuerpo y el foco es

ΔS= ΔS_c+ΔS_f>0

${\displaystyle \Delta S=mc\left(\ln \left(\frac{T_f}{T_i}\right)-\frac{T_f-T_i}{T_f}\right)}$

Proceso de N pasos

Para calentar un cuerpo de masa m y calor específico m desde una temperatura inicial T₀ hasta una temperatura final T_N, lo ponemos en contacto con N focos a las temperaturas T₁, T₂, T₃,...T_N, tal como se muestra en la figura

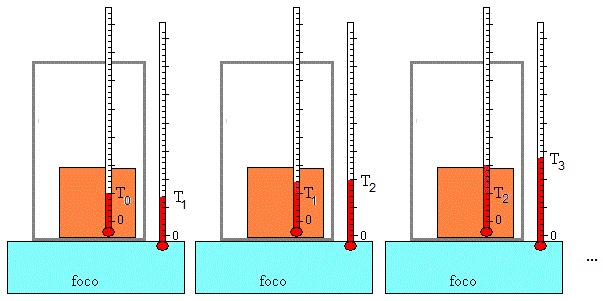
Primer paso

Colocamos un cuerpo de masa m y calor específico c cuya temperatura inicial es T_i=T₀ en contacto con un foco cuya temperatura es T_f=T₁. Al cabo de cierto tiempo, el cuerpo alcanza la temperatura del foco T_f

La variación de entropía del sistema formado por el cuerpo y el foco es

${\displaystyle \Delta S_1=mc\left(\ln \left(\frac{T_1}{T_0}\right)-\frac{T_1-T_0}{T_1}\right)}$

Segundo paso

Colocamos el cuerpo de masa m y calor específico c cuya temperatura inicial es T_i=T₁, en contacto con un foco cuya temperatura es T_f=T₂. Al cabo de cierto tiempo, el cuerpo alcanza la temperatura  del foco T_f

La variación de entropía del sistema formado por el cuerpo y el foco es

${\displaystyle \Delta S_2=mc\left(\ln \left(\frac{T_2}{T_1}\right)-\frac{T_2-T_1}{T_2}\right)}$

Etapa k

Colocamos el cuerpo de masa m y calor específico c cuya temperatura inicial es T_i=T_k-1, en contacto con un foco cuya temperatura es T_f=T_k. Al cabo de cierto tiempo, el cuerpo alcanza la temperatura del foco T_f

La variación de entropía del sistema formado por el cuerpo y el foco es

${\displaystyle \Delta S_k=mc\left(\ln \left(\frac{T_k}{T_{k-1}}\right)-\frac{T_k-T_{k-1}}{T_k}\right)}$

Etapa N

Colocamos el cuerpo de masa m y calor específico c cuya temperatura inicial es T_i=T_N-1, en contacto con un foco cuya temperatura es T_f=T_N. Al cabo de cierto tiempo, el cuerpo alcanza la temperatura  del foco T_f

La variación de entropía del sistema formado por el cuerpo y el foco es

${\displaystyle \Delta S_N=mc\left(\ln \left(\frac{T_N}{T_{N-1}}\right)-\frac{T_N-T_{N-1}}{T_N}\right)}$

Proceso completo

El proceso consta de una sucesión de N estados de equilibrio que lleva al cuerpo desde la temperatura T₀ a la temperatura T_N. La variación de entropía es la suma ΔS= ΔS₁+ΔS₂+ΔS₃+...ΔS_N

En la variación de la entropía del cuerpo (primer sumando de ΔS_i) el numerador del término i es el denominador del término i+1, al sumar los logaritmos se cancelan, por ejemplo, ln(a/b)+ln(c/a)=ln(c/b)

${\displaystyle \begin{array}{l}\Delta S=mc\left(\ln \left(\frac{T_1}{T_0}\right)-\frac{T_1-T_0}{T_1}\right)+mc\left(\ln \left(\frac{T_2}{T_1}\right)-\frac{T_2-T_1}{T_2}\right)+mc\left(\ln \left(\frac{T_3}{T_2}\right)-\frac{T_3-T_2}{T_3}\right)+\mathrm{...}\\ mc\left(\ln \left(\frac{T_N}{T_{N-1}}\right)-\frac{T_N-T_{N-1}}{T_N}\right)=mc\ln \left(\frac{T_N}{T_0}\right)-mc{\displaystyle \sum _{k=1}^N\left(1-\frac{T_{k-1}}{T_k}\right)}\end{array}}$

Progresión aritmética

En este caso, la temperatura del foco k es T_k=T₀+k(T_N-T₀)/N, k=1,2,3...N

Primer paso

La temperatura inicial es T_i=T₀ y la del foco es T_f=T₀+(T_N-T₀)/N.

${\displaystyle \Delta S_1=mc\left(\ln \left(\frac{(N-1)T_0+T_N}{N{T}_0}\right)-\frac{T_N-T_0}{(N-1)T_0+T_N}\right)}$

Segundo paso

La temperatura inicial es T_i= T₀+(T_N-T₀)/N y la del foco es T_f=T₀+2(T_N-T₀)/N.

${\displaystyle \Delta S_2=mc\left(\ln \left(\frac{(N-2)T_0+2T_N}{(N-1)T_0+T_N}\right)-\frac{T_N-T_0}{(N-2)T_0+2T_N}\right)}$

Etapa k

La temperatura inicial es T_i= T₀+(k-1)(T_N-T₀)/N y la del foco T_f=T₀+k(T_N-T₀)/N.

${\displaystyle \Delta S_k=mc\left(\ln \left(\frac{(N-k)T_0+k{T}_N}{(N-k+1)T_0+(k-1)T_N}\right)-\frac{T_N-T_0}{(N-k)T_0+k{T}_N}\right)}$

Etapa N

La temperatura inicial es T_i= T₀+(N-1)(T_N-T₀)/N, en contacto con un foco cuya temperatura es T_f=T_N.

${\displaystyle \Delta S_N=mc\left(\ln \left(\frac{N{T}_N}{T_0+(N-1)T_N}\right)-\frac{T_N-T_0}{N{T}_N}\right)}$

Proceso completo

${\displaystyle \Delta S=mc\ln \left(\frac{T_N}{T_0}\right)-mc\left(T_N-T_0\right){\displaystyle \sum _{k=1}^N\frac{1}{(N-k)T_0+k{T}_N}}}$

Ejemplo:

• La temperatura inicial del cuerpo es T₀=0ºC=273 K
• La temperatura final es T_N=80ºC=353 K
• La masa m del cuerpo y su calor específico c son tales que el producto m·c=1

Una etapa, N=1

Ponemos el cuerpo a la temperatura inicial de 273 K en contacto con un foco a la temperatura fija de 353 K

${\displaystyle \Delta S=\ln \left(\frac{353}{273}\right)-\frac{353-273}{353}=0.0304}$

Cuatro etapas, N=4

1. Ponemos el cuerpo a la temperatura inicial de 273 K en contacto con un foco a la temperatura de 273+80/4=293 K. La variación de entropía es

${\displaystyle \Delta S_1=\ln \left(\frac{293}{273}\right)-\frac{293-273}{293}=0.0024}$

2. El cuerpo ha alcanzado la temperatura de 293 K. Lo ponemos en contacto con un foco a la temperatura de 313 K. La variación de entropía es

${\displaystyle \Delta S_2=\ln \left(\frac{313}{293}\right)-\frac{313-293}{313}=0.0021}$

3. El cuerpo ha alcanzado la temperatura de 313 K. Lo ponemos en contacto con un foco a la temperatura de 333 K. La variación de entropía es

${\displaystyle \Delta S_3=\ln \left(\frac{333}{313}\right)-\frac{333-313}{333}=0.0019}$

4. El cuerpo ha alcanzado la temperatura de 333 K. Lo ponemos en contacto con un foco a la temperatura de 353 K. La variación de entropía es

${\displaystyle \Delta S_4=\ln \left(\frac{353}{333}\right)-\frac{353-333}{353}=0.0017}$

La variación de entropía del proceso que consta de cuatro estados de equilibrio es

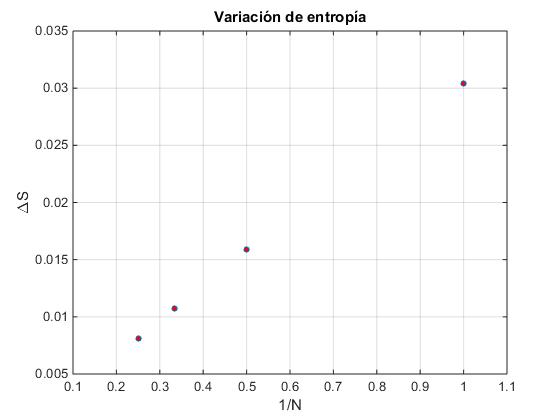
ΔS= ΔS₁+ΔS₂+ΔS₃+ΔS₄=0.0081

>> N=4;
>> T0=273;
>> TN=353;
>> i=1:4;
>> log(TN/T0)-(TN-T0)*sum(1./((N-i)*T0+i*TN))
ans =    0.0081

Que como vemos es mucho menor que en el proceso de una sola etapa.

Elaboramos un script para representar:

• En el eje vertical la variación de entropía ΔS
• En el eje horizontal la inversa 1/N del número de pasos

N=4; 
SS=zeros(N+1,1);
S=zeros(N+1,1);
T0=273; %temperatura inicial del cuerpo
TN=353; %temperatura final
S(1)=0;
for k=1:N
    for j=1:k
          Ti=T0+(j-1)*(TN-T0)/k; %temperatura inicial en cada etapa
          Tf=T0+j*(TN-T0)/k;      %temperatura final en cada etapa
         S(j+1)=S(j)+log(Tf/Ti)-(Tf-Ti)/Tf;
    end
 %variación de entropía total del proceso de k etapas
    SS(k)=S(k+1);
end
x=1./(1:N);
plot(x,SS(1:N),'o','markersize',4,'markerfacecolor','r')
xlim([0.1,1.1]) 
grid on
hold off
ylabel('\DeltaS')
xlabel('1/N')
title('Variación de entropía')

Cuando el número N de pasos es muy grande la suma de las variaciones de entropía del foco y del gas tiende a cero. ΔS_f+ΔS_c→0

Actividades

Se introduce

• La temperatura final del cuerpo T_N, en el control titulado Temperatura

• La temperatura inicial se ha fijado en T₀=0ºC=273 K

• La masa m del cuerpo y su calor específico c se han elegido de modo que el producto m·c=1

Se pulsa el botón titulado Nuevo.

• El número de pasos es N=1. El proceso consta de una sucesión de dos estados de equilibrio.

Se pulsa el botón titulado ►

• Se pone el cuerpo en contacto con un foco a la temperatura T₁. Se observa que la temperatura del cuerpo aumenta hasta alcanzar la temperatura final del foco.

Cuando el cuerpo ha alcanzado la temperatura final de equilibrio, se pulsa el botón titulado >>

• El número de pasos es N=2. El proceso consta de una sucesión de dos estados de equilibrio.

Se pulsa el botón titulado ►

y así, sucesivamente

En la parte derecha, se representa

• En el eje vertical, la variación de entropía ΔS

• En el eje horizontal, la inversa 1/N del número de pasos

Cuando el número N de pasos es muy grande la suma de las variaciones de entropía del foco y del gas tiende a cero.

Progresión geométrica

En este caso, la temperatura del foco k es

${\displaystyle $ T_k={\left(\frac{T_N}{T_0}\right)}^{\frac{k}{N}}{T}_0,k=\mathrm{1,2,...}N$}$

Seguimos los mismos pasos que en el apartado la progresión aritmética. La variación de entropía del proceso completo de N pasos es

${\displaystyle \Delta S=mc\ln \left(\frac{T_N}{T_0}\right)-mc{\displaystyle \sum _{k=1}^N\left(1-\frac{T_{k-1}}{T_k}\right)}=mc\left\{\ln \left(\frac{T_N}{T_0}\right)+N\left({\left(\frac{T_0}{T_N}\right)}^{\frac{1}{N}}-1\right)\right\}}$

Modificamos el script anterior, cambiando solamente dos líneas del código, las temperaturas inicial T_i y final T_f, en progresión aritmética por progresión geométrica

N=4; 
SS=zeros(N+1,1);
S=zeros(N+1,1);
T0=273; %temperatura inicial del cuerpo
TN=353; %temperatura final
S(1)=0;
for k=1:N
    for j=1:k
          Ti=T0*(TN/T0)^((j-1)/k); %temperatura inicial en cada etapa
          Tf=T0*(TN/T0)^(j/k);      %temperatura final
          S(j+1)=S(j)+log(Tf/Ti)-(Tf-Ti)/Tf;
    end
 %variación de entropía total del proceso de k etapas
    SS(k)=S(k+1);
end
x=1./(1:N);
plot(x,SS(1:N),'o','markersize',4,'markerfacecolor','r')
%xlim([0.1,1.1]) 
grid on
hold off
ylabel('\DeltaS')
xlabel('1/N')
title('Variación de entropía')

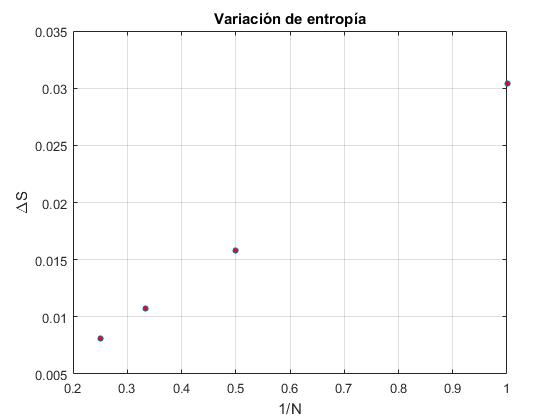
Obtenemos unos resultados similares, lo que indica que lo más relevante es el número N de focos y no la temperatura (comprendida entre la inicial T₀ y la final T_N) de los mismos.

>> log(TN/T0)+N*((T0/TN)^(1/N)-1)
ans =    0.0081
>> SS(N)
ans =    0.0081

Cuando el número N de pasos es muy grande la suma de las variaciones de entropía del foco y del gas tiende a cero, ΔS_f+ΔS_c→0, como demostraremos a continuación

Calculamos la variación de entropía ΔS, en el límite cuando N→∞. Llamamos s al segundo sumando

${\displaystyle s=N\left({\left(\frac{T_0}{T_N}\right)}^{\frac{1}{N}}-1\right)}$

entonces

${\displaystyle \frac{T_0}{T_N}={\left(1+\frac{s}{N}\right)}^N}$

Llamamos ahora, x=N/s

${\displaystyle \frac{T_0}{T_N}={\left[{\left(1+\frac{1}{x}\right)}^x\right]}^s}$

En el límite, cuando x→∞ o N→∞. La expresión entre corchetes es el número e

${\displaystyle \begin{array}{l}\frac{T_0}{T_N}=e^s\\ s=\ln \left(\frac{T_0}{T_N}\right)\end{array}}$

La variación de entropía del proceso completo cuando N→∞ es nula, el proceso es reversible

${\displaystyle \Delta S_{\infty }=mc\left\{\ln \left(\frac{T_N}{T_0}\right)+\ln \left(\frac{T_0}{T_N}\right)\right\}=0}$

Referencias

Calkin M. G., Kiang D., Entropy change and reversibility. Am. J. Phys. 51 (1) January 1983., pp. 78-79

E N Miranda. When an irreversible cooling (o heating) becomes reversible. Eur. J. Phys. 21 (2000) pp. 239-243