Sea un recipiente cilíndrico de sección S, perfectamente aislado, en posición vertical con un émbolo que separa una parte que está vacía a presión p=0, y la otra parte que contiene un gas.

Ecuación de los gases perfectos

Si que la temperatura absoluta del gas es T y su altura es y. La ecuación de los gases perfectos, nos relaciona la presión p=f/S, el volumen V=y·S y la temperatura T de una masa de gas o de su número n de moles.

p·V =nRT
f·y =nRT

Donde f es la fuerza que ejerce el gas sobre el émbolo debido a la presión, y R=8.3143 J/(K·mol) es la constante de los gases

La energía interna del gas ideal es

${\displaystyle U=n{c}_{v}T=\frac{pSy}{RT}\frac{R}{\gamma -1}T=\frac{f·y}{\gamma -1}}$

El índice γ=5/3 para un gas monoatómico y γ=7/5 para un gas diatómico

Antes de formular la ecuación del movimiento, vamos a estudiar algunas situaciones especiales.

Situación inicial de equilibrio

En la situación inicial, el émbolo de masa se m₀ está en equilibrio bajo la acción de dos fuerzas:

• su peso m₀g

• la fuerza que ejerce el la presión p₀ del gas encerrado en el recipiente f₀=p₀·S. Siendo S el área del émbolo, o el área de la base del recipiente.

m₀g=f₀

La energía inicial del gas ideal es

${\displaystyle U_0=n{c}_v{T}_0=\frac{f_0·y_0}{\gamma -1}}$

Instante inicial

En el instante t=0, se coloca sobre el émbolo un bloque de masa m_p. El émbolo se desequilibra, ya que el peso (m₀+m_p)g=mg es mayor que la fuerza que ejerce la presión del gas f₀=p₀·S.

Posición de equilibrio

El émbolo se mueve hacia abajo, comprimiendo el gas, hasta que la fuerza f que ejerce el gas sobre el émbolo debido a su presión, se vuelve a igualar al peso mg

En la nueva situación de equilibrio y_e, el peso del conjunto formado por émbolo y el bloque mg se hace igual a la fuerza que ejerce la presión del gas f_e=p_e·S.

mg= f_e

La ecuación de la transformación adiabática entre la posición inicial y la de equilibrio, nos permite calcular y_e.

${\displaystyle \begin{array}{l}{p}_0{V}_0^{\gamma }=p_e{V}_e^{\gamma }{f}_0{y}_0^{\gamma }=f_e{y}_e^{\gamma }\\ y_e=y_0{\left(\frac{m_0}{m}\right)}^{1/\gamma }\end{array}}$

La temperatura del gas T_e se calcula a partir de la ecuación del gas ideal

${\displaystyle \begin{array}{l}{f}_e{y}_e=nR{T}_e\\ \frac{m·y_e}{T_e}=\frac{m_0{y}_0}{T_0}\end{array}}$

Conocida y_e, calculamos la velocidad v_e del conjunto émbolo-bloque aplicando el principio de conservación de la energía.

${\displaystyle \frac{m_{0}g·y_0}{\gamma -1}+mg{y}_0=mg{y}_e+\frac{1}{2}m{v}_e^2+\frac{mg·y_e}{\gamma -1}}$

En el miembro izquierdo, tenemos

• La energía interna inicial del gas,
• La energía potencial del conjunto émbolo-bloque cuando está en la posición inicial y₀.

En el miembro de la derecha tenemos

• La energía potencial final del conjunto émbolo-bloque,
• su energía cinética,
• la energía interna del gas en la posición final y_e.

Máxima comprensión del gas

El movimiento del conjunto bloque-émbolo prosigue, hasta que su velocidad se hace cero, el gas se comprime al máximo. En esta posición el émbolo y el bloque no están en equilibrio.

El principio de conservación de la energía se escribe para la posición y_m de máximo desplazamiento.

${\displaystyle \frac{m_{0}g·y_0}{\gamma -1}+mg{y}_0=mg{y}_m+\frac{f_m{y}_m}{\gamma -1}}$

En esta posición, la energía potencial del conjunto bloque-émbolo se convierte enteramente en energía interna del gas ideal.

La ecuación de la transformación adiabática, se escribe

${\displaystyle \begin{array}{l}{p}_0{V}_0^{\gamma }=p_m{V}_m^{\gamma }{f}_0{y}_0^{\gamma }=f_m{y}_m^{\gamma }\\ f_m=m_{0}g{\left(\frac{y_0}{y_m}\right)}^{\gamma }\end{array}}$

Introduciendo f_m en la ecuación de la conservación de la energía, obtenemos una ecuación en y_m cuya raíz es preciso calcular empleando procedimientos numéricos.

Conocido f_m e y_m, la temperatura T_m del gas se calcula a partir de la ecuación del gas ideal

${\displaystyle \frac{f_m·y_m}{T_m}=\frac{m_0{y}_0}{T_0}}$

Cuando se llega a esta posición, se ha completado un semiperiodo de la oscilación. El émbolo y el bloque vuelven a recorrer el camino inverso hasta que regresan a la posición inicial de partida en el instante t=0.

Ecuación del movimiento

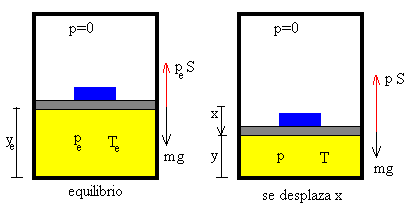
Supongamos que el émbolo y el bloque están en la posición y_e de equilibrio estable. Si se desplaza x de dicha posición, la fuerza que ejerce el gas sobre el émbolo f tiende a restaurar al conjunto émbolo-bloque a la posición de equilibrio. Un comportamiento similar al del sistema formado por una partícula y un muelle elástico

Las fuerzas sobre el conjunto de los dos cuerpos, cuando el émbolo se encuentra en la posición y=y_e-x, son

• el peso mg
• la fuerza que ejerce el la presión p del gas encerado en el recipiente f=p·S.

La segunda ley de Newton se escribe

${\displaystyle m\frac{d^{2}x}{d{t}^2}=mg-f}$

Calculamos la fuerza f a partir de la transformación adiabática

${\displaystyle \begin{array}{l}{p}_0{V}_0^{\gamma }=p{V}^{\gamma }{f}_0{y}_0^{\gamma }=f{y}^{\gamma }\\ f=m_{0}g{\left(\frac{y_0}{y_e-x}\right)}^{\gamma }\\ \frac{d^{2}x}{d{t}^2}=g\left(1-{\left(\frac{y_e}{y_e-x}\right)}^{\gamma }\right)y_e=y_0{\left(\frac{m_0}{m}\right)}^{1/\gamma }\end{array}}$

Resolvemos la ecuación diferencial por procedimientos numéricos, con las condiciones iniciales t=0, v=dx/dt=0, x=-(y₀-y_e).

Si x<<y_e. hacemos la aproximación

${\displaystyle {\left(\frac{y_e}{y_e-x}\right)}^{\gamma }={\left(1-\frac{x}{y_e}\right)}^{-\gamma }\approx 1+\frac{\gamma x}{y_e}}$

La ecuación diferencial se escribe

${\displaystyle \frac{d^{2}x}{d{t}^2}+\frac{g\gamma }{y_e}x=0}$

que es la ecuación diferencial de un MAS de frecuencia angular ω²=gγ/y_e

Balance energético

Cuando el émbolo desciende, la energía potencial del conjunto de los dos cuerpos disminuye, aumenta la energía cinética, y la energía interna del gas aumenta al incrementarse la presión y reducirse el volumen. Cuando el émbolo asciende ocurre el proceso inverso.

Si se desprecian las pérdidas, el principio de conservación de la energía se escribe

${\displaystyle \frac{m_{0}g{y}_0}{\gamma -1}+mg{y}_0=mgy+\frac{1}{2}m{v}^2+\frac{f·y}{\gamma -1}}$

• Los términos del miembro izquierdo, son la energía del sistema formado por el gas, el émbolo y la pesa en el instante inicial t=0.

• Los términos del miembro derecho, son la energía del sistema en el instante t, v es la velocidad del conjunto bloque-émbolo en dicho instante

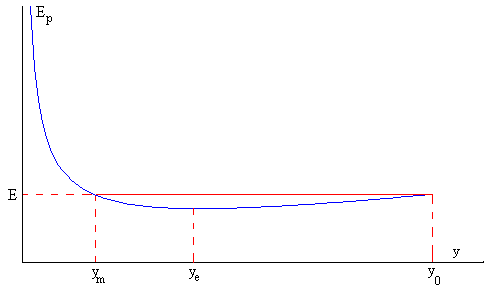
En la figura, se representa la energía potencial E_p en función de la posición y del émbolo

${\displaystyle E_p=mgy+\frac{f·y}{\gamma -1}f{y}^{\gamma }=\text{cte}}$

Para una energía total E

${\displaystyle E=\frac{m_{0}g{y}_0}{\gamma -1}+mg{y}_0}$

se señala la posición de partida y₀, la de equilibrio y_e, en el mínimo de la curva de energía potencial y la de máxima comprensión y_m cuando E=E_p, y la velocidad v=0.

Supongamos que el sistema formado por el conjunto bloque-émbolo y el gas es aislado. La ecuación del balance energético es

${\displaystyle \frac{m_{0}g{y}_0}{\gamma -1}+mg{y}_0=mgy+\frac{1}{2}m{v}^2+\frac{f·y}{\gamma -1}}$

En el miembro izquierdo, tenemos la energía interna del gas y potencial del conjunto bloque-émbolo, a la derecha, la energía cinética y potencial del conjunto bloque-émbolo y la energía interna final del gas.

El émbolo llega a la posición de equilibrio estable y=y_e después de cierto tiempo, con velocidad v=0. En esta posición de equilibrio, la fuerza f que ejerce el gas sobre el émbolo debido a la presión se anula con el peso del conjunto formado por el bloque y el émbolo f=(m₀+m_p)g=mg

${\displaystyle \frac{m_{0}g{y}_0}{\gamma -1}+mg{y}_0=mg{y}_e+\frac{mg·y_e}{\gamma -1}}$

La energía potencial del conjunto émbolo-bloque correspondiente a la altura (y₀-y_e) se convierte enteramente en energía interna del gas en la posición final de equilibrio y_e. Despejando y_e

${\displaystyle y_e=\left(\frac{m_0}{m_0+m_p}+\gamma -1\right)\frac{y_0}{\gamma }}$

Un caso particular interesante, es aquél en el que la masa del bloque m_p se hace muy grande, el volumen del gas no se reduce a cero, como cabría esperar, sino que tiende a un valor límite.

${\displaystyle \underset{m\to \infty }{\lim }{y}_e=\frac{\gamma -1}{\gamma }{y}_0}$

Si no hay pérdidas de calor, la energía potencial del conjunto bloque-émbolo en la posición inicial se convierte en energía interna del gas en la posición final de equilibrio.

Ejemplos

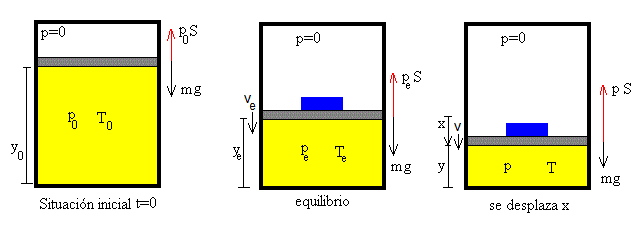
En la figura, se representa la situación inicial, la situación de equilibrio y cuando el conjunto émbolo-bloque se ha desplazado x=y_e-y de la posición de equilibrio

Los datos del sistema formado por el gas y el émbolo de la figura son los siguientes:

• La temperatura 20 ºC=293 K

• Se selecciona gas monoatómico

La fuerza que ejerce el gas sobre el émbolo es igual al peso del émbolo

f₀=p₀·S= m₀g=1·9.8 N

Conociendo el número n=0.002 de moles y la temperatura T₀=293 K calculamos el volumen o la posición inicial y₀ del émbolo, aplicando la ecuación de los gases perfectos,

${\displaystyle \begin{array}{l}{p}_0{V}_0=nR{T}_0\\ m_{0}g·y_0=nR{T}_0{y}_0=\frac{0.002·8.3143·293}{1·9.8}=0.497\text{m}=\text{49}\text{.7}\text{cm}\end{array}}$

• masa del bloque m_p=3 kg

Situación de equilibrio

El émbolo desciende y comprime el gas. Detenemos el movimiento cuando el émbolo y el bloque pasan por la posición de equilibrio. El peso del conjunto bloque-émbolo (m₀+m_p)g=mg se igualan a la fuerza f_e que ejerce el gas sobre el émbolo debido a la presión.

f_e=(1+3)·9.8 =39.2 N

Este es el valor numérico de la fuerza f que se señala en el eje vertical de la gráfica. Observamos las fuerzas que actúan sobre el émbolo representadas por flechas. La resultante de las fuerzas que actúan sobre el conjunto embolo-bloque debe de ser cero o próximo a cero.

La ecuación de la transformación adiabática nos proporciona la altura y_e del émbolo

${\displaystyle y_e=y_0{\left(\frac{m_0}{m}\right)}^{1/\gamma }{y}_e=0.497{\left(\frac{1}{4}\right)}^{3/5}=0.216\text{m}=\text{21}\text{.6}\text{cm}}$

Calculamos ahora, la temperatura en esta situación de equilibrio

${\displaystyle m·y_e=\frac{m_0{y}_0}{T_0}{T}_{e}4·0.216=\frac{1·0.497}{293}{T}_e}$

T_e=510 K

La ecuación de la conservación de la energía nos proporciona la velocidad del émbolo

${\displaystyle \begin{array}{l}\frac{m_{0}g·y_0}{\gamma -1}+mg{y}_0=mg{y}_e+\frac{1}{2}m{v}_e^2+\frac{mg·y_e}{\gamma -1}\\ \frac{1·9.8·0.497}{\frac{5}{3}-1}+4·9.8·0.497=4·9.8·0.216+\frac{1}{2}4v_e^2+\frac{4·9.8·0.216}{\frac{5}{3}-1}\end{array}}$

v_e=1.67 m/s

Máxima compresión del gas

El gas continúa comprimiéndose hasta que la velocidad el conjunto émbolo-bloque sea cero, (el dato de la velocidad se observa en la parte superior derecha)

El principio de conservación de la energía. Poniendo v=0.

${\displaystyle \begin{array}{l}\frac{m_{0}g·y_0}{\gamma -1}+mg{y}_0=mg{y}_m+\frac{f_m·y_m}{\gamma -1}\\ \frac{1·9.8·0.497}{\frac{5}{3}-1}+4·9.8·0.497=4·9.8·y_m+\frac{f_m·y_m}{\frac{5}{3}-1}\end{array}}$

De la ecuación de la transformación adiabática tenemos

${\displaystyle \begin{array}{l}{f}_m{y}_m^{\gamma }=f_0{y}_0^{\gamma }\\ f_m{y}_m^{\gamma }=1·9.8·{0.497}^{5/3}\end{array}}$

Introduciendo f_m en la primera ecuación, se llega una ecuación en y_m cuya raíz se obtiene por procedimientos numéricos.

n=0.002; %número de moles
R=8.3143; %constante de los gases
T0=293; %temperatura inicial
m0=1; %masa del émbolo
mp=3; %masa del bloque
m=mp+m0; %masa total
gamma=5/3; %gas monoatómico

y0=n*R*T0/(m0*9.8); %altura inicial de equilibrio
ye=y0*(m0/m)^(1/gamma); %posición de equilibrio 
%máxima compresnsión del gas

f=@(x) m0*9.8*y0/(gamma-1)+m*9.8*y0-m*9.8*x-
(m0*9.8*y0^gamma)*x^(1-gamma)/(gamma-1);
ym=fzero(f, ye) %máxima comprensión del gas
fm=(m0*9.8*y0^gamma)/ym^gamma %presión (fuerza) en esta posición

ym =    0.0868
fm =  179.6621

Por ejemplo, pulsando en el botón   Ⅱ   (Pausa) cuando la velocidad v está cercana al valor cero, el programa interactivo nos da los valores de y_m=8.7 cm y f_m=179.66 N.

Comprobamos que estos valores son conformes con las ecuaciones de la trasformación adiabática y el principio de conservación de la energía. Se ha de tener en cuenta, que para la posición de máximo desplazamiento, un pequeño error en la medida de y_m produce un gran error en la medida de f_m.

Cuando se llega a esta posición, el émbolo empieza a ascender, hasta que llega a la posición inicial, completando un periodo.

El periodo de las oscilaciones de pequeña amplitud es

${\displaystyle P=\frac{2\pi }{\omega }=2\pi \sqrt{\frac{y_e}{g\gamma }}P=2\pi \sqrt{\frac{0.216}{9.8·\frac{5}{3}}}=0.72\text{s}}$

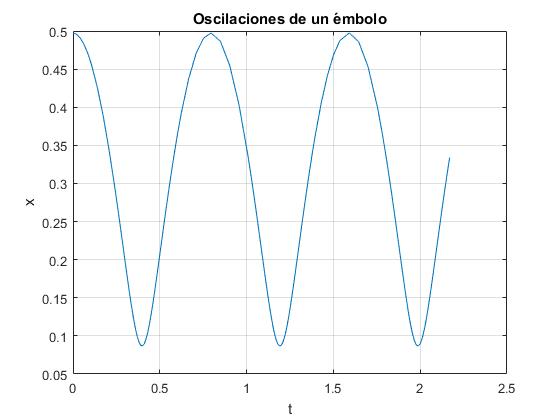
Representamos la altura del émbolo y en función del tiempo t, resolviendo la ecuación diferencial del movimiento por procedimientos numéricos

n=0.002; %número de moles
R=8.3143; %constante de los gases
T0=293; %temperatura inicial
m0=1; %masa del émbolo
mp=3; %masa del bloque
m=mp+m0; %masa total
gamma=5/3; %gas monoatómico

y0=n*R*T0/(m0*9.8); %altura inicial de equilibrio
ye=y0*(m0/m)^(1/gamma); %posición de equilibrio 

P=2*pi*sqrt(ye/(9.8*gamma)); %periodo de las pequeñas oscilaciones
%resuelve la ecuación diferencial
x0=[(ye-y0);0];
fg=@(t,x) [x(2); 9.8*(1.0-(ye/(ye-x(1)))^gamma)];
[t,x]=ode45(fg,[0,3*P],x0);
plot(t,ye-x(:,1)) %tiempo-desplazamiento
xlabel('t')
ylabel('x');
title('Oscilaciones de un émbolo')
grid on

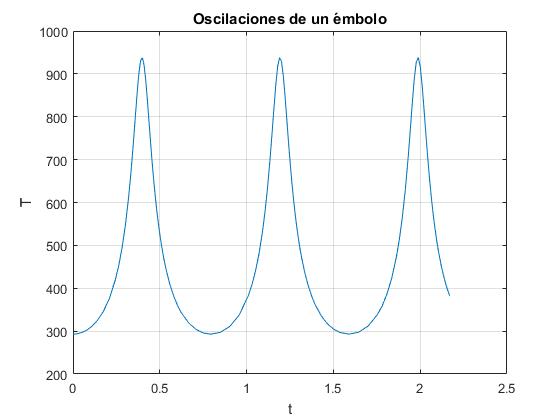
Representamos la temperatura del gas en función del tiempo

    ... %del script previo
[t,x]=ode45(fg,[0,3*P],x0);
f=(m0*9.8*y0^gamma)./(ye-x(:,1)).^gamma;
T=T0*(f.*(ye-x(:,1)))/(m0*9.8*y0);
plot(t,T) %tiempo-temperatura
xlabel('t')
ylabel('T');
title('Oscilaciones de un émbolo')
grid on

Del mismo modo, se puede representar la presión del gas f en función del tiempo t

Actividades

Se introduce

• El tipo de gas, monoatómico o diatómico, activando el botón de radio correspondiente.

• La temperatura inicial T₀ del gas encerrado en el recipiente, en el control titulado Temperatura.

• La masa del émbolo m₀ se ha fijado en un kg.

• El número de moles se ha fijado en n=0.002 mol

• La masa del bloque m_p (en kg), en el control titulado Pesa

Se pulsa el botón titulado Nuevo

Se pone el bloque sobre el émbolo y observamos su movimiento descendente, comprimiendo el gas.

Se representan las fuerzas sobre el conjunto émbolo-bloque,

• El peso mg
• La fuerza f que ejerce el gas sobre el émbolo debida a la presión

y se proporciona el dato de la resultante f-mg.

Se proporcionan los datos del tiempo y velocidad de émbolo en la parte superior derecha. La temperatura en la parte inferior del recipiente.

En la parte derecha, se representa la fuerza f que ejerce la presión del gas sobre el émbolo en función de la posición y del émbolo. La curva tiene la forma f·y^γ=cte, que es la ecuación de una transformación adiabática. La constante se determina conociendo la fuerza f₀ (presión) y la altura del émbolo y₀ (volumen) en el instante t=0.

Finalmente, se representa, mediante un diagrama en forma de tarta

• la energía interna del gas
• la energía cinética del conjunto bloque-émbolo
• su energía potencial

en el que observamos la transformación de unos tipos de energía en otros.

Oscilaciones de un émbolo unido a un muelle elástico

Un recipiente cilíndrico vertical contiene n=2 moles de un gas ideal a la presión p₀, volumen V₀ y temperatura T₀=300 K.

Un émbolo de masa m=10 kg y sección A=500 cm² comprime el gas, dejando la parte superior del recipiente vacío. Un muelle elástico de constante k=mgA/V₀ unido al émbolo está sujeto en la parte superior del recipiente.

Se supone que no hay pérdidas de calor, ni rozamiento al desplazarse el émbolo y que los procesos en el gas son adiabáticos. El gas es monoatómico, γ=5/3.

En la situación inicial, se comprime el gas hasta que su volumen es V₀/2. Se suelta el émbolo con velocidad inicial v=0, nula.

Volumen del gas

Vamos a calcular el volumen V del gas cuando la velocidad del émbolo es $v=\sqrt{\frac{4g{V}_0}{5A}}$

Volumen inicial de gas a la temperatura T₀

${\displaystyle \begin{array}{l}{p}_{0}A=mg\\ p_0{V}_0=nR{T}_0,V_0=\frac{nR{T}_{0}A}{mg}\end{array}}$

1. Trabajo realizado para que el volumen del gas se modifique de V₀/2 a V

En una transformación adiabática

${\displaystyle \begin{array}{l}{p}_0{V}_0^{\gamma }=p{V}^{\gamma }\\ W_{gas}={\displaystyle \underset{V_0/2}{\overset{V}{\int }}p·dV=p_0{V}_0^{\gamma }}{\displaystyle \underset{V_0/2}{\overset{V}{\int }}\frac{dV}{V^{\gamma }}=}\frac{p_0{V}_0^{\gamma }}{1-\gamma }\left(V^{1-\gamma }-{\left(\frac{V_0}{2}\right)}^{1-\gamma }\right)\\ W_{gas}=\frac{mg{V}_0^{\gamma }}{A\left(1-\gamma \right)}\left(V^{1-\gamma }-{\left(\frac{V_0}{2}\right)}^{1-\gamma }\right)\end{array}}$

2. Cambio en la energía potencial del émbolo

${\displaystyle E_p=mg\Delta h=mg\frac{V-\frac{V_0}{2}}{A}}$

3. Cambio en la energía potencial del muelle elástico

El muelle no está deformado cuando V=V₀

${\displaystyle \begin{array}{l}{E}_{muelle}=\frac{1}{2}k{x}^2-\frac{1}{2}k{x}_0^2=\frac{1}{2}\left(\frac{mgA}{V_0}\right){\left(\frac{V_0-V}{A}\right)}^2-\frac{1}{2}\left(\frac{mgA}{V_0}\right){\left(\frac{V_0-\frac{V_0}{2}}{A}\right)}^2\\ E_{muelle}=\frac{mg{V}_0}{2A}\left({\left(1-\frac{V}{V_0}\right)}^2-\frac{1}{4}\right)\end{array}}$

4. Energía cinética del émbolo

${\displaystyle E_k=\frac{1}{2}m{v}^2=\frac{1}{2}m{\left(\sqrt{\frac{4g{V}_0}{5A}}\right)}^2=\frac{2mg{V}_0}{5A}}$

Conservación de la energía

${\displaystyle \begin{array}{l}{W}_{gas}=E_p+E_k+E_{muelle}\\ \frac{mg{V}_0^{\gamma }}{A\left(1-\gamma \right)}\left(V^{1-\gamma }-{\left(\frac{V_0}{2}\right)}^{1-\gamma }\right)=mg\frac{2V-V_0}{2A}+\frac{2mg{V}_0}{5A}+\frac{mg{V}_0}{2A}\left({\left(1-\frac{V}{V_0}\right)}^2-\frac{1}{4}\right)\\ \frac{1}{1-\gamma }\left(s^{1-\gamma }-\frac{1}{2^{1-\gamma }}\right)=\frac{2s-1}{2}+\frac{2}{5}+\frac{1}{2}\left({\left(1-s\right)}^2-\frac{1}{4}\right),s=\frac{V}{V_0}\\ \frac{1}{1-\gamma }\left(s^{1-\gamma }-\frac{1}{2^{1-\gamma }}\right)-\frac{s^2}{2}-\frac{11}{40}=0\end{array}}$

Para gas es monoatómico, γ=5/3, obtenemos la ecuación transcendente

${\displaystyle \frac{3}{2}\left(s^{-2/3}-2^{2/3}\right)+\frac{s^2}{2}+\frac{11}{40}=0}$

Representemos la función f(s)=0

f=@(x) (x.^(-2/3)-2^(2/3))*3/2+x.^2/2+11/40;
fplot(f,[0,2])
ylim([-1,3])
grid on
xlabel('s')
ylabel('f(s)')
title('Ecuación transcendente')

Vemos que hay dos raíces de la ecuación transcendente. Las calculamos, utilizando la función fzero de MATLAB

>> fzero(f,[0.5,1])
ans =    0.7413
>>  fzero(f,[1,2])
ans =    1.3027

El resultado es V=0.7413V₀, V=1.3027V₀

Oscilaciones del émbolo

Las fuerzas sobre el émbolo son

• La fuerza que ejerce el muelle deformado, kx
• la fuerza que ejerce la presión del gas, pA
• El peso del émbolo, mg

La ecuación del movimiento es

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=mg-kx-pA\\ p=\frac{p_0{V}_0^{\gamma }}{V^{\gamma }}=\frac{mg}{A}\frac{V_0^{\gamma }}{{\left(V_0-Ax\right)}^{\gamma }}=\frac{mg}{A}\frac{1}{{\left(1-\frac{Ax}{V_0}\right)}^{\gamma }}\\ \frac{d^{2}x}{d{t}^2}=g\left(1-\frac{A}{V_0}x-\frac{1}{{\left(1-\frac{A}{V_0}x\right)}^{\gamma }}\right)\end{array}}$

Suponiendo que Ax<<V₀

${\displaystyle \begin{array}{l}\frac{1}{{\left(1-\frac{A}{V_0}x\right)}^{\gamma }}\approx 1+\gamma \frac{Ax}{V_0}\\ \frac{d^{2}x}{d{t}^2}+\left(1+\gamma \right)\frac{gA}{V_0}x=0\end{array}}$

>> syms k g x;
>> taylor(1/(1-k*x)^g,x,0,'order',2)
ans =g*k*x + 1

Es la ecuación de un movimiento armónico simple de frecuencia angular

${\displaystyle {\omega }_0^2=\left(1+\gamma \right)\frac{gA}{V_0}=\left(1+\gamma \right)\frac{p_{0}gA}{nR{T}_0}=\left(1+\gamma \right)\frac{m{g}^2}{nR{T}_0}}$

Resolvemos la ecuación diferencial, por el procedimiento numérico ode45 de MATLAB, con las siguientes condiciones iniciales: en el instante t=0, la posición del émbolo es x₀=(V₀/2)/A, con velocidad inicial nula

La ecuación de un MAS es

${\displaystyle \begin{array}{l}x=A\sin \left({\omega }_{0}t+\phi \right)\\ v=\frac{dx}{dt}=A{\omega }_0\cos \left({\omega }_{0}t+\phi \right)\end{array}}$

En el instante t=0, v=0, φ=π/2. La posición inicial es x=x₀, por lo que A=x₀. La ecuación del MAS es

${\displaystyle x=x_0\cos \left({\omega }_{0}t\right)}$

Comparamos la solución numérica con su aproximación analítica, comprobamos que no es correcta ya que no se cumple que Ax<<V₀ con los datos del problema

A=500e-4; %sección
gamma=5/3;
V0=2*8.314*300*A/(10*9.8); %volumen inicial
x0=(V0/2)/A; %posición inicial
f=@(t,x) [x(2);9.8*(1-A*x(1)/V0-1/(1-A*x(1)/V0)^gamma)]; 
[t,x]=ode45(f,[0,20],[x0,0]);
w=sqrt((1+gamma)*9.8*A/V0);
xp=@(t) x0*cos(w*t);
hold on
fplot(xp,[0,20])
plot(t,x(:,1))
hold off
grid on
xlabel('t')
legend('aprox.','numérica','location','best')
ylabel('x');
title('Oscilaciones de un émbolo')

Referencias

APhO Problems and Solutions. 2005, Indonesia. Spring Cylinder With Massive Piston