Oscilaciones de un émbolo que separa dos gases contenidos en un recinto adiabático
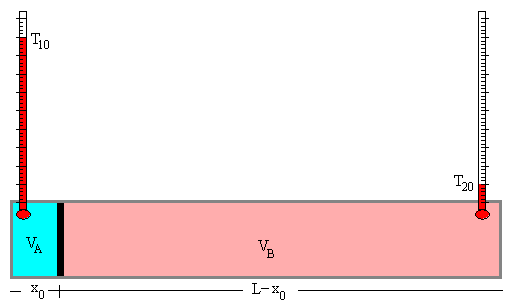
Un cilindro de sección S y longitud L está cerrado por ambos extremos, contiene un émbolo que divide el volumen en dos partes A y B, ambos contienen la misma cantidad de un gas ideal, un mol. El cilindro y el émbolo están adiabáticamente aislados. El émbolo está sujeto de modo que los volúmenes iniciales de cada parte son, respectivamente V10=S·x0, V20=S(L-x0). Las temperaturas iniciales del gas en cada una de las dos partes son T10 y T20.
En el instante t=0, se libera el pistón y suponemos que el émbolo se mueve sin rozamiento. Vamos a determinar el estado final de equilibrio.
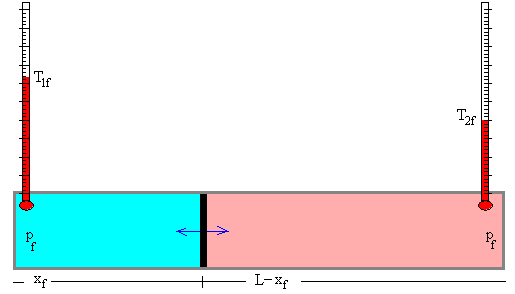
El sistema alcanzará el equilibrio cuando las presiones de los gases separados por el émbolo sea la misma p1f=p2f=pf
Aplicamos la ecuación de los gases ideales a cada una de las partes
Como el sistema es aislado, la energía total permanece constante
Los volúmenes de los gases cambian, pero el volumen total es constante e igual al inicial que ocupaban los gases.
pf·V1f=nRT1f
pf·V2f=nRT2f
U1f+U2f=U10+U20
La energía interna de un gas ideal solamente depende de la temperatura
T1f+T2f=T10+T20
V10+V20=V1f+V2f
Despejamos la temperaturas finales y la presión final
Ahora bien, de estas ecuaciones no podemos despejar los volúmenes finales ni las temperaturas finales. Como veremos más adelante, la formulación de un modelo de gas ideal o ciertas hipótesis acerca del acerca del movimiento del émbolo y su interacción con las moléculas del gas, nos va a permitir describir la evolución desde el estado inicial al final de equilibrio.
Oscilaciones del émbolo
Supongamos que el émbolo se mueve sin rozamiento. El principio de conservación de la energía para el sistema aislado formado por los dos gases y el émbolo se escribe para un mol de gas.
El primer término es la energía cinética del émbolo de masa M. El segundo, la energía interna de un mol de gas contenido en la parte izquierda y el tercero, la energía interna de un mol de gas contenido en la parte derecha.
Los dos gases experimentan una transformación adiabática
Recuérdese que cp=cv+R y γ=cp/cv
El principio de conservación de la energía se escribe.
El segundo término es la energía potencial Ep(x). que se representa en la figura. Para una energía total E, el émbolo oscila entre las dos posiciones x0 y x1 señaladas en la figura, con un determinado periodo
gamma=5.0/3; %indice adiabático del gas
T10=80+273; %temperaturas iniciales
T20=20+273;
R=8.3143; %constante de los gases
L=1.0; %longitud de los recipientes
x0=0.1; %posición inicial del émbolo
E=R*(T10+T20)/(gamma-1); %energía total
f=@(x) R*(T10*(x0./x).^(gamma-1)+T20*((L-x0)./(L-x)).^(gamma-1))/(gamma-1);
fplot(f,[0.05,0.85])
line([0,1],[E,E], 'color','r')
xlabel('x')
ylabel('Ep')
title ('Energía potencial')
grid on
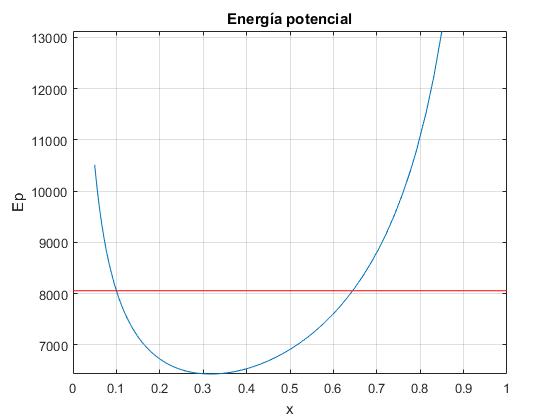
El émbolo parte de la posición x0, en el instante t=0, y llega a la posición de máximo desplazamiento x1 cuando su velocidad es dx/dt=0 (la energía potencial Ep se hace igual a la energía total E). Para calcular esta posición, es preciso resolver por procedimientos numéricos la ecuación trascendente
>> f=@(x) T10*(x0/x)^(gamma-1)+T20*((L-x0)/(L-x))^(gamma-1)-T10-T20; >> fzero(f,[0.3,0.9]) ans = 0.6443
Ecuación del movimiento
Derivamos la ecuación de la conservación de la energía respecto con respecto del tiempo
La ecuación del movimiento se escribe
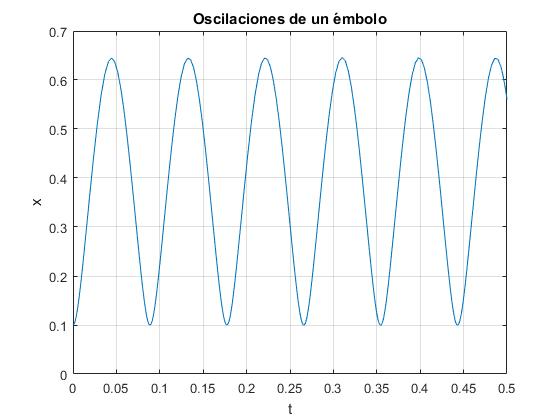
Se resuelve esta ecuación diferencial de segundo orden por procedimiento numéricos con las siguientes condiciones iniciales: en el instante t=0, x=x0, y dx/dt=0.
gamma=5.0/3; %indice adiabático del gas
T10=80+273; %temperaturas iniciales
T20=20+273;
R=8.3143; %constante de los gases
L=1.0; %longitud de los recipientes
x0=0.1; %posición inicial del émbolo
m=10; %masa del émbolo
fg=@(t,x) [x(2); R*(T10*x0^(gamma-1)/x(1)^gamma-T20*(L-x0)^(gamma-1)
/(L-x(1))^gamma)/m];
[t,x]=ode45(fg,[0,0.5],[x0,0]);
plot(t,x(:,1)) %tiempo-desplazamiento
xlabel('t')
ylabel('x');
title('Oscilaciones de un émbolo')
grid on
Actividades
Se introduce
-
La temperatura inicial T10 en ºC del gas situado en la parte izquierda del cilindro, en el control titulado Temperatura 1
-
La temperatura inicial T20 en ºC del gas situado en la parte derecha del cilindro, en le control titulado Temperatura 2
-
La masa M del émbolo en kg, en el control titulado Masa
-
La posición inicial x0, en el control titulado Posición. Determina el volumen inicial de los gases proporcional a x0 y (1.0-x0), respectivamente.
Se pulsa el botón titulado Nuevo
Se observa el movimiento oscilatorio del émbolo
Los termómetros marcan la temperatura de los dos gases en K: cuando el gas se comprime adiabáticamente se eleva su temperatura, cuando se expande su temperatura disminuye.
En la parte superior, se representa la energía potencial Ep(x) del émbolo y la energía total mediante una recta horizontal, señalándose los dos puntos de intersección x0 y x1 que son los puntos de retorno en los que la velocidad del émbolo se anula. El mínimo de la curva Ep(x) señala la posición de equilibrio, la fuerza sobre el émbolo es nula, la velocidad del émbolo es máxima.
El contador de tiempo en la parte superior, nos permite medir el periodo de las oscilaciones.
Aproximación al equilibrio
Haciendo que el émbolo conduzca el calor cuando hay una difeencia de temperaturas entre la parte izquierda y derecha del recipiente nos aproximamos a la situación de equilibrio
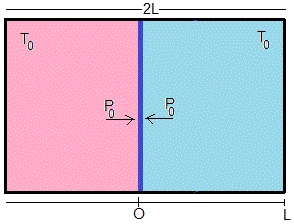
Un cilindro horizontal de sección A y longitud 2L cuyas paredes son perfectamente aislantes contiene un gas ideal a la temperatura T0 y a la presión P0. Un émbolo de masa m que divide al recipiente en dos partes iguales se puede desplazar sin rozamiento.
El número n de moles en cada una de las dos partes es
Se supondrá que la presión y temperatura del gas ideal son uniformes en cada instante (no hay diferencias entre dos puntos del recinto que lo contiene)
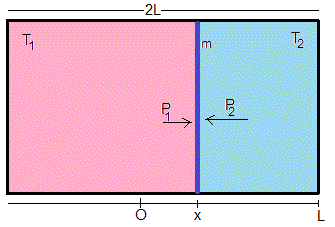
En el instante t=0, el émbolo se desplaza x0 de la posición de equilibrio y se suelta. Vamos a determinar la posición x del émbolo, su velocidad v, la presión P1 y la temperatura T1 de la parte izquierda y la presión P2 y la temperatura T2 de la parte derecha, en función del tiempo t
Como el número de moles de gas es el mismo en cada una de las dos partes
Evolución del sistema
Se describe el comportamiento del sistema mediante tres ecuaciones diferenciales y la ecuación de estado del gas ideal
La ecuación del movimiento del émbolo de masa m es
Transferencia de calor entre las dos partes
La ley de Fourier establece que el flujo de calor (energía por unidad de área y unidad de tiempo) es proporcional al gradiente de temperatura.
Suponiendo que la temperatura T2 de la parte derecha es mayor que la la de la parte izquierda T1. El calor absorbido por la parte izquierda es
donde h es un coeficiente efectivo de transferencia de calor con unidades W/(m2K)
El primer principio de la termodinámica para la parte izquierda se escribe
cv es el calor específico a volumen constante
Análogamente, para la parte derecha,
Conservación de la energía
Se trata de un sistema aislado, la energía total permanece constante. La energía total se compone de tres términos
- La energía interna de la parte izquierda
- La energía interna de la parte derecha
- La energía cinética del émbolo
La energía inicial corresponde a 2n moles de gas ideal a la temperatura T0
T10 y T20 son las temperaturas iniciales de cada una de las dos partes
Solución numérica del sistema de tres ecuaciones diferenciales
Antes de resolver el sistema de tres ecuaciones diferenciales, es conveniente expresarlas en términos de magnitudes adimensionales
La ecuación de estado
La ecuación del movimiento del émbolo. Primera ecuación diferencial
La segunda ecuación diferencial
La tercera ecuación diferencial
El principio de conservación de la energía
Del mismo modo
Resolvemos el sistema de tres ecuaciones diferenciales
Con las condiciones iniciales: en el instante τ=0, el desplazamiento es ξ0<1, la temperaturas iniciales son iguales Γ1=1 y Γ2=1
El sistema de tres ecuaciones diferenciales se resuelve mediante el procedimiento
Ejemplo 1
- El cociente tc/th=1
- Calor específico a volumen constante, cv=5R/2
- El desplazamiento inicial ξ0=0.25
- La velocidad inicial dξ/dt0=0
- La temperatura inicial de la parte izquierda Γ10=1
- La temperatura inicial de la parte derecha Γ20=1
% x(1) es xi, x(2) es dxi/dtau, x(3) es T1 , x(4) es T2
k=1; %cociente t_c/t_h
cv=2.5; %c_v/R
fg=@(t,x)[x(2); x(3)/(1+x(1))-x(4)/(1-x(1)); k*(x(4)-x(3))-
x(3)*x(2)/(cv*(1+x(1))); -k*(x(4)-x(3))+x(4)*x(2)/(cv*(1-x(1)))];
[t,x]=ode45(fg,[0,30],[0.25,0,1,1]);
plot(t,x(:,1))
grid on
xlabel('\tau')
ylabel('\xi');
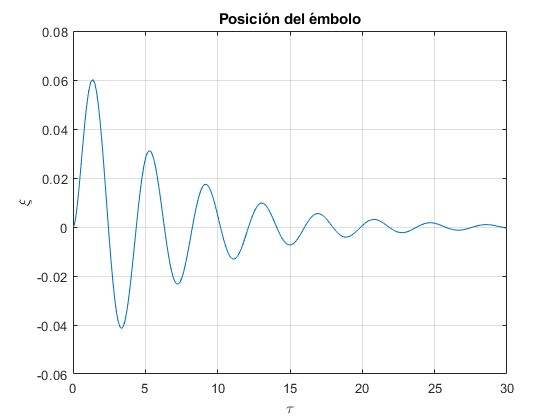
title('Posición del émbolo')
figure
plot(t,x(:,2))
grid on
xlabel('\tau')
ylabel('d\xi/d\tau');
title('Velocidad del émbolo')
figure
hold on
plot(t,x(:,3))
plot(t,x(:,4))
hold off
legend('1','2','Location', 'best')
grid on
xlabel('\tau')
ylabel('\Gamma');
title('Temperaturas ')
figure
hold on
plot(t,x(:,3)./(1+x(:,1)))
plot(t,x(:,4)./(1-x(:,1)))
hold off
legend('1','2','Location', 'best')
grid on
xlabel('\tau')
ylabel('p');
title('Presión del gas')
figure
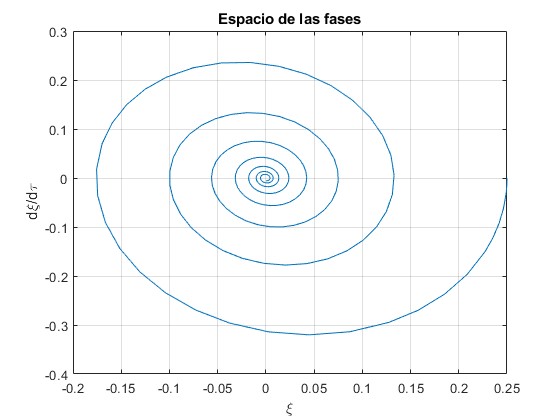
plot(x(:,1),x(:,2))
grid on
xlabel('\xi')
ylabel('d\xi/d\tau');
title('Espacio de las fases')
%conservación de la energía
E=x(:,4)+x(:,3)+x(:,2).^2/(2*cv);
Posición del émbolo ξ en función del tiempo τ
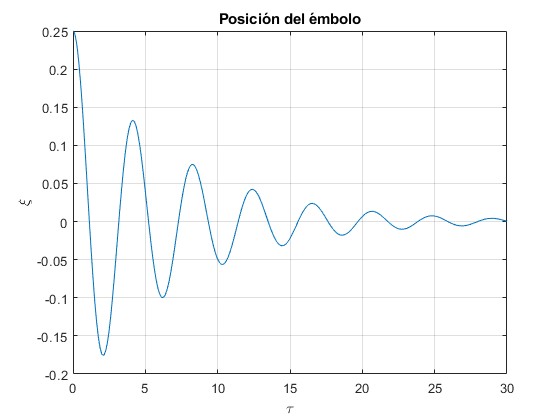
Velocidad del émbolo dξ/dτ en función del tiempo τ
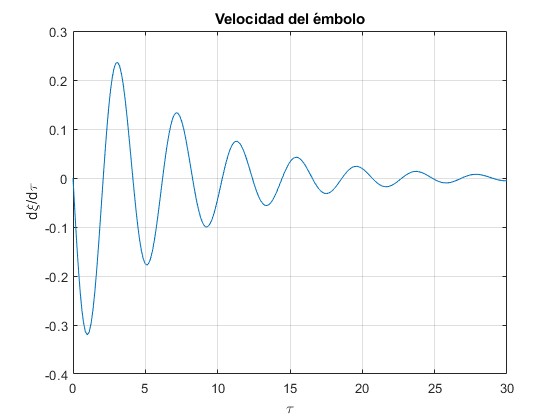
Velocidad del émbolo dξ/dτ en función de la posición ξ
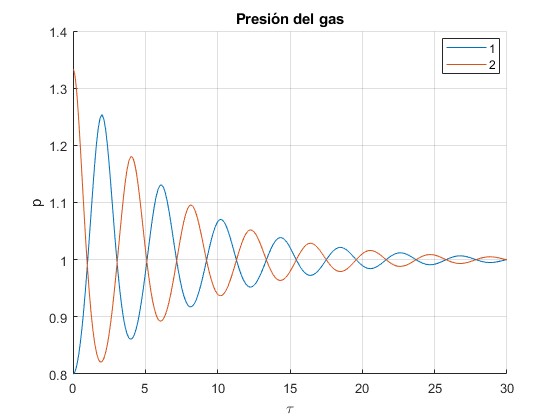
Presión p del gas en función del tiempo τ
Se emplea la ecuación de estado para calcular la presión conocido el desplazamiento del émbolo ξ y la temperatura Γ
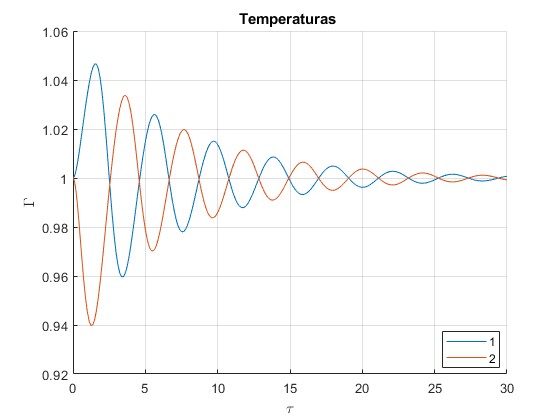
Temperaturas del gas Γ1 y Γ2
Comprobamos la conservación de la energía
>> E=x(:,4)+x(:,3)+x(:,2).^2/(2*cv)
E =
2.0000
2.0000
....
2.0000
2.0000
2.0000
Ejemplo 2
- El desplazamiento inicial ξ0=0
- La velocidad inicial dξ/dt0=0
- La temperatura inicial de la parte izquierda Γ10=1.25
- La temperatura inicial de la parte derecha Γ20=1
Posición del émbolo ξ en función del tiempo τ
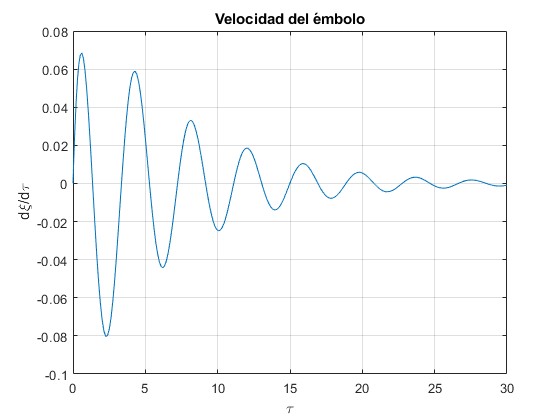
Velocidad del émbolo dξ/dτ en función del tiempo τ
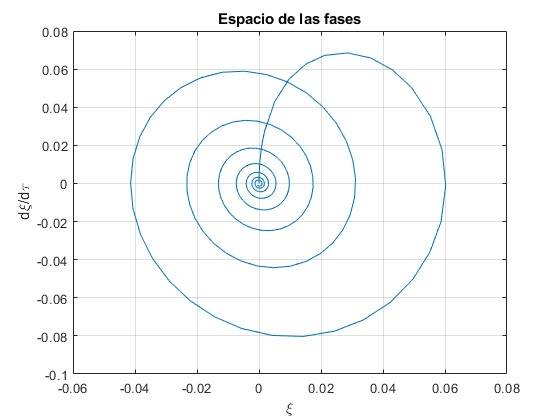
Velocidad del émbolo dξ/dτ en función de la posición ξ
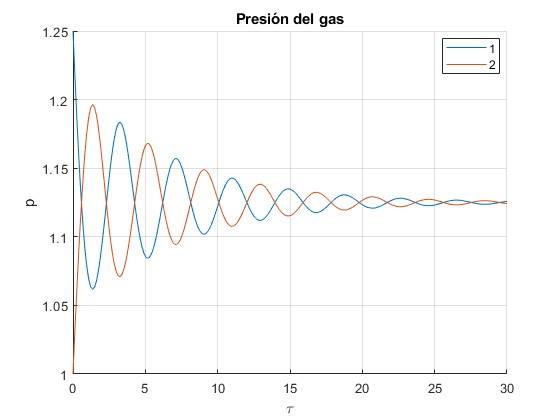
Presión p del gas en función del tiempo τ
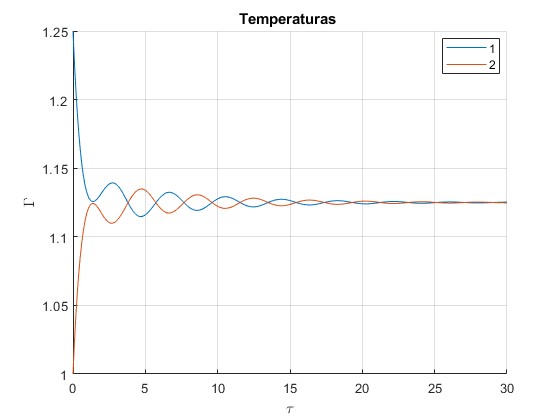
Temperaturas del gas Γ1 y Γ2
Comprobamos la conservación de la energía
>> E=x(:,4)+x(:,3)+x(:,2).^2/(2*cv)
E=
2.2500
2.2500
....
2.2500
Referencias
ZHU Han,ZHOU Yang. Kinetic properties of a heat conducting piston oscillating in an adiabatic cylinder container. 20 April 2003, Volume 22, Issue 4

