La ecuación de la trayectoria en coordenadas polares es

${\displaystyle r=\frac{d}{1+\cos \theta }}$

La mínima distancia al centro de fuerzas d/2, se da cuando la posición angular θ=0

d=1;
ang=-2*pi/3:pi/180:2*pi/3;
r=d./(1+cos(ang));
polar(ang,r)
title('Trayectoria parabólica')

Ecuación de la parábola en coordenadas rectangulares

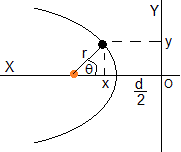
La distancia r entre el vértice de la parábola y el foco, θ=0, es d/2

Establecemos los ejes tal como se muestra en la figura. El origen O a una distancia d/2 del vértice o d del foco. La posición (x,y) del cuerpo celeste es

x=d-rcosθ
y=rsinθ

La ecuación de la trayectoria se escribe

${\displaystyle \begin{array}{l}d=r+r\cos \theta \\ d=\sqrt{{\left(d-x\right)}^2+y^2}+(d-x)\end{array}}$

Elevando al cuadrado

${\displaystyle \begin{array}{l}x=\sqrt{{\left(d-x\right)}^2+y^2}\\ y^2-2dx+d^2=0\end{array}}$

Que es la ecuación de una parábola

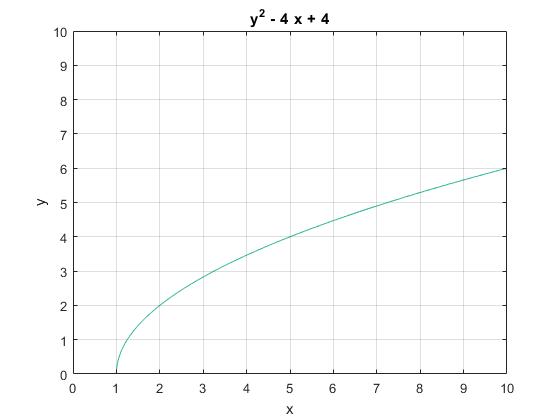
>> syms x y;
>> d=2;
>> ezplot(y^2-2*d*x+d^2,[0,10])
>> grid on

Tiempo que tarda en recorrer un arco de parábola

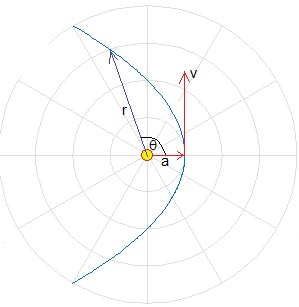
El Sol se encuentra en el centro, la mínima distancia entre el Sol y el cometa, cuando la posición angular θ=0, es a=d/2. La energía E del cometa es cero. Su velocidad máxima v está relacionada con la distancia de máximo acercamiento a. El momento angular L es constante

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}^2+\left(-G\frac{Mm}{a}\right)=0\\ L=mva\sin 90=m\sqrt{2GMa}\end{array}}$

Vamos ahora a calcular el tiempo que tarda un cometa en desplazarse un determinado arco de parábola.

En la página titulada Trayectorias elípticas, calculamos el periodo o tiempo que tarda en dar una vuelta un cuerpo celeste que describe una trayectoria elíptica.

En el intervalo de tiempo entre t y t+dt, el radio vector se desplaza un intervalo angular entre θ y θ+dθ y barre el área de un triángulo de base (r·dθ) y altura r.

${\displaystyle \frac{r\left(r·d\theta \right)}{2}=\frac{r^2·d\theta }{2}}$

El momento angular en coordenadas polares se escribe

${\displaystyle L=m{r}^2\frac{d\theta }{dt}}$

Teniendo en cuenta que el momento angular es constante, integramos

${\displaystyle {\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{r^2}{2}}d\theta =\frac{L}{2m}{\displaystyle \underset{0}{\overset{t}{\int }}dt}}$

El tiempo t, que tarda en desplazarse un cometa desde θ=0, a θ es

${\displaystyle t=\frac{1}{\sqrt{2GMa}}{\displaystyle \underset{0}{\overset{\theta }{\int }}{\left(\frac{2a}{1+\cos \theta }\right)}^{2}d\theta =}\frac{a^2}{\sqrt{2GMa}}{\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{1}{{\cos }^4(\theta /2)}}d\theta =\frac{2a^2}{\sqrt{2GMa}}{\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{1}{{\cos }^4\phi }}d\phi }$

Para integrar, hacemos los cambios

${\displaystyle \begin{array}{l}y=\tan \phi dy=\frac{d\phi }{{\cos }^2\phi }\\ 1+{\tan }^2\phi =\frac{1}{{\cos }^2\phi }\\ {{\displaystyle \int }}^{\text{}}\frac{d\phi }{{\cos }^4\phi }={{\displaystyle \int }}^{\text{}}\frac{dy}{{\cos }^2\phi }={{\displaystyle \int }}^{\text{}}(1+y^2)dy=\left(y+\frac{y^3}{3}\right)=\tan \phi +\frac{{\tan }^3\phi }{3}\end{array}}$

El tiempo t que tarda el cometa en desplazarse un ángulo θ es

${\displaystyle t=\sqrt{\frac{2a^3}{GM}}\left(\tan \frac{\theta }{2}+\frac{{\tan }^3(\theta /2)}{3}\right)}$

Tiempo de tránsito de un cometa

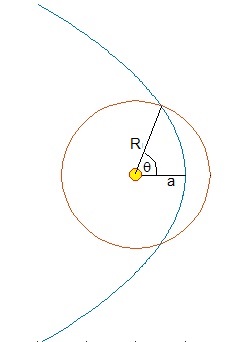
Supongamos que un cometa atraviesa la órbita circular de la Tierra de radio R, tal como se muestra en la figura

Calculamos el ángulo θ de intersección de las dos trayectorias

${\displaystyle R=\frac{2a}{1+\cos \theta }}$

Teniendo en cuenta la identidad trigonométrica

${\displaystyle {\tan }^2\frac{\theta }{2}=\frac{1-\cos \theta }{1+\cos \theta }}$

Tenemos que

${\displaystyle \tan \frac{\theta }{2}=\sqrt{\frac{R-a}{a}}}$

Por simetría, el tiempo de tránsito es el doble que el calculado entre 0 y θ

${\displaystyle t=\frac{2}{3}\left(2a+R\right)\sqrt{\frac{2}{GM}\left(R-a\right)}}$

El extremo de t (máximo o mínimo) se obtienen derivando t respecto de a e igualando a cero, dt/da=0. El resultado es a=R/2, por lo que el tiempo de tránsito se reduce a

${\displaystyle t=\frac{4}{3}\sqrt{\frac{R^3}{GM}}}$

Este tiempo es una fracción del periodo o tiempo que tarda en dar una vuelta la Tierra

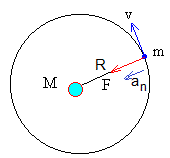
La Tierra describe una órbita circular de radio R. Para calcular su velocidad v aplicamos la dinámica del movimiento circular uniforme

${\displaystyle m\frac{v^2}{R}=G\frac{Mm}{R^2}v=\sqrt{\frac{GM}{R}}}$

El tiempo que tarda en recorrer la órbita circular es

${\displaystyle P=\frac{2\pi R}{v}=2\pi \sqrt{\frac{R^3}{GM}}}$

El tiempo de tránsito de un cometa con a=R/2 que pasa justamente entre el Sol y la Tierra es una fracción del periodo P (un año) de la Tierra

${\displaystyle t=\frac{2}{3\pi }P}$

Referencias

Ahmad A. Kamal. 1000 Solved Problems in Classical Physics. An Exercise Book. Springer (2011). Problemas 5.46 y 5.47 pp. 226-228