El estado de un electrón de masa m_e alrededor de un núcleo de masa m_p se describe mediante la ecuación de Schrödinger en coordenadas esféricas

${\displaystyle \frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial \psi }{\partial r}\right)+\frac{1}{r^2\sin \theta }\frac{\partial }{\partial \theta }\left(\sin \theta \frac{\partial \psi }{\partial \theta }\right)+\frac{1}{r^2{\sin }^2\theta }\frac{{\partial }^2\psi }{\partial {\phi }^2}+\frac{2\mu }{{\hslash }^2}\left(E-V(r)\right)\psi =0}$

Donde μ es la masa reducida y r es la distancia entre el electrón y el núcleo.

${\displaystyle \mu =\frac{m_p{m}_e}{m_p+m_e}=\frac{m_e}{1+\frac{m_e}{m_p}}\approx m_e}$

La energía potencial V(r) del único electrón de un átomo de hidrógeno o ion hidrogenoide (He⁺, Li⁺⁺, ...) de número atómico Z es

${\displaystyle V(r)=-\frac{1}{4\pi {\epsilon }_0}\frac{Z{e}^2}{r}}$

En este apartado, estudiaremos el átomo de hidrógeno Z=1, y supondremos que el núcleo es el centro fijo de fuerzas de atracción electrostática

Para resolver la ecuación de Schrödinger transformaremos una ecuación diferencial en derivadas parciales en un sistema de tres ecuaciones diferenciales dependientes unicamente de las variables r, θ y φ, respectivamente

En primer lugar, supondremos que la solución de la ecuación de Schrödinger es el producto de dos funciones: una que describe el estado del electrón en la dirección radial r y otra en la dirección angular (θ, φ)

${\displaystyle \psi (r,\theta ,\phi )=R(r)·Y(\theta ,\phi )}$

Separamos la variable r de las variables θ y φ

${\displaystyle \begin{array}{l}Y\frac{d}{dr}\left(r^2\frac{dR}{dr}\right)+R\frac{1}{\sin \theta }\frac{\partial }{\partial \theta }\left(\sin \theta \frac{\partial Y}{\partial \theta }\right)+R\frac{1}{{\sin }^2\theta }\frac{{\partial }^{2}Y}{\partial {\phi }^2}+\frac{2m_e}{{\hslash }^2}{r}^2\left(E-V(r)\right)RY=0\\ \frac{1}{R}\frac{d}{dr}\left(r^2\frac{dR}{dr}\right)+\frac{2m_e}{{\hslash }^2}{r}^2\left(E-V(r)\right)=-\frac{1}{Y}\left\{\frac{1}{\sin \theta }\frac{\partial }{\partial \theta }\left(\sin \theta \frac{\partial Y}{\partial \theta }\right)+\frac{1}{{\sin }^2\theta }\frac{{\partial }^{2}Y}{\partial {\phi }^2}\right\}\end{array}}$

La parte izquierda no depende de (θ, φ) y la parte derecha no depende de r, por tanto, ambas términos se igualan a una constante que denominamos λ₁. La ecuación diferencial en derivadas parciales se transforma en el sistema de dos ecuaciones diferenciales

${\displaystyle \{\begin{array}{l}\frac{1}{r^2}\frac{d}{dr}\left(r^2\frac{dR}{dr}\right)+\left\{\frac{2m_e}{{\hslash }^2}\left(E-V(r)\right)-\frac{{\lambda }_1}{r^2}\right\}R=0\\ \frac{1}{\sin \theta }\frac{\partial }{\partial \theta }\left(\sin \theta \frac{\partial Y}{\partial \theta }\right)+\frac{1}{{\sin }^2\theta }\frac{{\partial }^{2}Y}{\partial {\phi }^2}+{\lambda }_{1}Y=0\end{array}}$

La parte angular

Supondremos que la solución Y(θ, φ) de la segunda ecuación diferencial en derivadas parciales es el producto de dos funciones que dependen solamente de θ y φ, respectivamente

${\displaystyle Y(\theta ,\phi )=\Theta (\theta )\Phi (\phi )}$

La parte angular se estudia en la página titulada La ecuación de Schrödinger en coordenadas esféricas con λ₁=l(l+1), y m=0, ±1, ±2, ...±l es decir, 2l+1 valores

Los primeros armónicos esféricos $Y_{l,m}\left(\theta ,\phi \right)$ son

${\displaystyle \begin{array}{l}{Y}_{\mathrm{0,0}}\left(\theta ,\phi \right)=\frac{1}{2\sqrt{\pi }}\\ Y_{\mathrm{1,0}}\left(\theta ,\phi \right)=\frac{1}{2}\sqrt{\frac{3}{\pi }}\cos \theta \\ Y_{\mathrm{1,}\pm 1}\left(\theta ,\phi \right)=\left(-1\right)\sqrt{\frac{3}{4\pi }\frac{1}{2!}}\left(-\sin \theta \right)e^{\pm i\phi }=\frac{1}{2}\sqrt{\frac{3}{2\pi }}\sin \theta ·e^{\pm i\phi }\\ Y_{\mathrm{2,0}}\left(\theta ,\phi \right)=\sqrt{\frac{5}{4\pi }\frac{2!}{2!}}\frac{1}{2}(3{\cos }^2\theta -1)=\frac{1}{4}\sqrt{\frac{5}{\pi }}(3{\cos }^2\theta -1)\\ Y_{\mathrm{2,}\pm 1}\left(\theta ,\phi \right)=\left(-1\right)\sqrt{\frac{5}{4\pi }\frac{1!}{3!}}\left(-3\cos \theta ·\sin \theta \right)e^{\pm i\phi }=\frac{1}{2}\sqrt{\frac{15}{2\pi }}\cos \theta ·\sin \theta ·e^{\pm i\phi }\\ Y_{\mathrm{2,}\pm 2}\left(\theta ,\phi \right)={\left(-1\right)}^2\sqrt{\frac{5}{4\pi }\frac{1}{4!}}3{\sin }^2\theta ·e^{\pm i2\phi }=\frac{1}{4}\sqrt{\frac{15}{2\pi }}{\sin }^2\theta ·e^{\pm i2\phi }\\ Y_{\mathrm{3,0}}\left(\theta ,\phi \right)=\sqrt{\frac{7}{4\pi }\frac{3!}{3!}}\frac{1}{2}(5{\cos }^3\theta -3\cos \theta )=\frac{1}{4}\sqrt{\frac{7}{\pi }}(5{\cos }^3\theta -3\cos \theta )\\ Y_{\mathrm{3,}\pm 1}\left(\theta ,\phi \right)=\left(-1\right)\sqrt{\frac{7}{4\pi }\frac{2!}{4!}}\left(-\frac{3}{2}(5{\cos }^2\theta -1)\sin \theta \right)e^{\pm i\phi }=\frac{1}{8}\sqrt{\frac{21}{\pi }}(5{\cos }^2\theta -1)\sin \theta ·e^{\pm i\phi }\\ Y_{\mathrm{3,}\pm 2}\left(\theta ,\phi \right)={\left(-1\right)}^2\sqrt{\frac{7}{4\pi }\frac{1!}{5!}}15\cos \theta {\sin }^2\theta ·e^{\pm i2\phi }=\frac{1}{4}\sqrt{\frac{105}{2\pi }}\cos \theta {\sin }^2\theta ·e^{\pm i2\phi }\\ Y_{\mathrm{3,}\pm 3}\left(\theta ,\phi \right)={\left(-1\right)}^3\sqrt{\frac{7}{4\pi }\frac{1}{6!}}\left(-15{\sin }^3\theta \right)e^{\pm i3\phi }=\frac{1}{8}\sqrt{\frac{35}{\pi }}{\sin }^3\theta ·e^{\pm i3\phi }\end{array}}$

Parte radial

Hay que resolver la ecuación diferencial

${\displaystyle \frac{d}{dr}\left(r^2\frac{dR}{dr}\right)+\left\{\frac{2m_e}{{\hslash }^2}\left(E+\frac{e^2}{4\pi {\epsilon }_{0}r}\right)r^2-l(l+1)\right\}R=0}$

Hacemos el cambio de variable r=aρ. Denominaremos R(r)= u(ρ)

${\displaystyle \begin{array}{l}\frac{d}{d\rho }\left({\rho }^2\frac{du}{d\rho }\right)+\left\{\frac{2m_e}{{\hslash }^2}\left(E+\frac{e^2}{4\pi {\epsilon }_{0}a\rho }\right)a^2{\rho }^2-l(l+1)\right\}u=0\\ \frac{d}{d\rho }\left({\rho }^2\frac{du}{d\rho }\right)+\left\{\frac{2m_e{a}^2}{{\hslash }^2}E{\rho }^2+\frac{m_{e}a}{{\hslash }^2}\frac{e^2}{2\pi {\epsilon }_0}\rho -l(l+1)\right\}u=0\\ \frac{d}{d\rho }\left({\rho }^2\frac{du}{d\rho }\right)+\left\{-\epsilon {\rho }^2+\rho -l(l+1)\right\}u=\mathrm{0,}\{\begin{array}{l}a=\frac{2\pi {\epsilon }_0{\hslash }^2}{m_e{e}^2}=\frac{a_0}{2}\\ \epsilon =-\frac{2m_e{a}^2}{{\hslash }^2}E\end{array}\\ \frac{d^{2}u}{d{\rho }^2}+\frac{2}{\rho }\frac{du}{d\rho }+\frac{1}{\rho }u-\frac{l(l+1)}{{\rho }^2}u=\epsilon u\end{array}}$

Donde a₀ es el radio de Bohr

Comportamiento asintótico

• Cuando ρ es grande

${\displaystyle \frac{d^{2}u}{d{\rho }^2}\approx \epsilon u}$

La solución de esta ecuación diferencial es

${\displaystyle u\approx A\exp \left(\sqrt{\epsilon }\rho \right)+B\exp \left(-\sqrt{\epsilon }\rho \right)}$

El coeficiente A deberá ser cero, para que la solución sea finita para ρ→∞. Cuando ρ es grande u(ρ) es proporcional a $\exp \left(-\sqrt{\epsilon }\rho \right)$

• Cuando ρ es pequeño

${\displaystyle \begin{array}{l}{\rho }^2\frac{d^{2}u}{d{\rho }^2}+2\rho \frac{du}{d\rho }+2\rho u-l(l+1)u={\rho }^2\epsilon u\\ {\rho }^2\frac{d^{2}u}{d{\rho }^2}-l(l+1)u\approx 0\end{array}}$

Buscamos una solución de la forma u=ρ^s, obtenemos la ecuación de segundo grado

s(s-1)-l(l+1)=0. Las raíces de la ecuación de segundo grado en s son

${\displaystyle s=\frac{1\pm (2l+1)}{2}=\{\begin{array}{l}l+1\\ -l\end{array}}$

La segunda no puede ser ya que ρ^-l→∞ cuando ρ→0. Cerca del origen el comportamiento de u(ρ) es proporcional a ρ^l+1

Conociendo el comportamiento asintótico, buscamos una solución para la ecuación diferencial radial de la forma

${\displaystyle \begin{array}{l}u=\exp \left(-\sqrt{\epsilon }\rho \right){\rho }^{l}v(\rho )\\ \frac{du}{d\rho }=-\sqrt{\epsilon }\exp \left(-\sqrt{\epsilon }\rho \right){\rho }^{l}v+l\exp \left(-\sqrt{\epsilon }\rho \right){\rho }^{l-1}v+\exp \left(-\sqrt{\epsilon }\rho \right){\rho }^l\frac{dv}{d\rho }\\ \frac{d^{2}u}{d{\rho }^2}=-\sqrt{\epsilon }\left(-\sqrt{\epsilon }\exp \left(-\sqrt{\epsilon }\rho \right){\rho }^{l}v+l\exp \left(-\sqrt{\epsilon }\rho \right){\rho }^{l-1}v+\exp \left(-\sqrt{\epsilon }\rho \right){\rho }^l\frac{dv}{d\rho }\right)+\\ l\left(-\sqrt{\epsilon }\exp \left(-\sqrt{\epsilon }\rho \right){\rho }^{l-1}v+(l-1)\exp \left(-\sqrt{\epsilon }\rho \right){\rho }^{l-2}v+\exp \left(-\sqrt{\epsilon }\rho \right){\rho }^{l-1}\frac{dv}{d\rho }\right)+\\ -\sqrt{\epsilon }\exp \left(-\sqrt{\epsilon }\rho \right){\rho }^l\frac{dv}{d\rho }+l\exp \left(-\sqrt{\epsilon }\rho \right){\rho }^{l-1}\frac{dv}{d\rho }+\exp \left(-\sqrt{\epsilon }\rho \right){\rho }^l\frac{d^{2}v}{d{\rho }^2}\end{array}}$

La ecuación diferencial en u(ρ) se convierte en

${\displaystyle \rho \frac{d^{2}v}{d{\rho }^2}+2\left(l+1-\sqrt{\epsilon }\rho \right)\frac{dv}{d\rho }+\left(1-2\sqrt{\epsilon }(l+1)\right)v=0}$

Hacemos otro cambio de variable llamando y(x) a v(ρ)

${\displaystyle \begin{array}{l}x=2\sqrt{\epsilon }\rho \\ \frac{d}{d\rho }=2\sqrt{\epsilon }\frac{d}{dx}\\ x\frac{d^{2}y}{d{x}^2}+2\left(l+1-\frac{x}{2}\right)\frac{dy}{dx}+\left(\frac{1}{2\sqrt{\epsilon }}-(l+1)\right)y=0\end{array}}$

Llamando a $n=\frac{1}{2\sqrt{\epsilon }}$, la ecuación diferencial se transforma en

${\displaystyle x\frac{d^{2}y}{d{x}^2}+\left(2(l+1)-x\right)\frac{dy}{dx}+\left(n-l-1\right)y=0}$

Si n es un entero positivo, las energías permitidas son

${\displaystyle \begin{array}{l}\epsilon =\frac{1}{4n^2}\\ -\frac{2m_e}{{\hslash }^2}{\left(\frac{2\pi {\epsilon }_0{\hslash }^2}{m_e{e}^2}\right)}^{2}E=\frac{1}{4n^2}\\ E_n=-\frac{m_e{e}^4}{8{\epsilon }_0^2{h}^2}\frac{1}{n^2}\end{array}}$

El mismo resultado que en el modelo de Bohr

Polinomios asociados de Laguerre

La ecuación diferencial y su solución, los polinomios asociados de Laguerre, son

${\displaystyle \begin{array}{l}x\frac{d^{2}y}{d{x}^2}+\left(m+1-x\right)\frac{dy}{dx}+ny=0\\ L_n^m(x)=(n+m)!{\displaystyle \sum _{k=0}^n\frac{{\left(-1\right)}^k}{(n-k)!(k+m)!k!}{x}^k}\end{array}}$

Generamos los polinomios asociados $L_n^m(x)$ con el siguiente código

syms x k;
for n=0:3
    for m=0:n
        disp([n,m])
        pol_n_m=factorial(n+m)*symsum((-1)^k*x^k/(factorial(n-k)*
factorial(m+k)*factorial(k)),k,0,n)
    end
end

      0     0    pol_n_m =1
      1     0    pol_n_m =1 - x
      1     1    pol_n_m =2 - x
      2     0    pol_n_m =x^2/2 - 2*x + 1
      2     1    pol_n_m =x^2/2 - 3*x + 3
      2     2    pol_n_m =x^2/2 - 4*x + 6
      3     0    pol_n_m =- x^3/6 + (3*x^2)/2 - 3*x + 1
      3     1    pol_n_m =- x^3/6 + 2*x^2 - 6*x + 4
      3     2    pol_n_m =- x^3/6 + (5*x^2)/2 - 10*x + 10
      3     3    pol_n_m =- x^3/6 + 3*x^2 - 15*x + 20

${\displaystyle \begin{array}{l}{L}_0^0(x)=1\\ L_1^0(x)=1-x\\ L_1^1(x)=2-x\\ L_2^0(x)=\frac{1}{2}{x}^2-2x+1\\ L_2^1(x)=\frac{1}{2}{x}^2-3x+3\\ L_2^2(x)=\frac{1}{2}{x}^2-4x+6\end{array}}$

Solución de la ecuación diferencial en y(x)

Ahora estamos en condiciones de encontrar la solución de la ecuación diferencial en y(x), a continuación en v(ρ), en u(ρ) y finalmente, R(r)

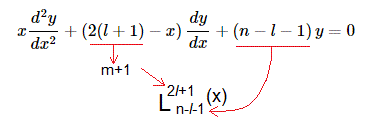
La solución son los polinomios asociados de Laguerre

${\displaystyle y(x)=L_{n-l-1}^{2l+1}(x)}$

Con los cambios de variable que hemos efectuado

${\displaystyle \begin{array}{l}v(\rho )=L_{n-l-1}^{2l+1}\left(2\sqrt{\epsilon }\rho \right)\\ u(\rho )=\exp \left(-\sqrt{\epsilon }\rho \right){\rho }^l{L}_{n-l-1}^{2l+1}\left(2\sqrt{\epsilon }\rho \right)\end{array}}$

Multiplicamos la última expresión por un factor para que los paréntesis contengan la misma variable, $\sqrt{\epsilon }\rho$

${\displaystyle \begin{array}{l}u(\rho )=\exp \left(-\sqrt{\epsilon }\rho \right){\left(2\sqrt{\epsilon }\rho \right)}^l{L}_{n-l-1}^{2l+1}\left(2\sqrt{\epsilon }\rho \right)\\ R(r)=A·\exp \left(-\sqrt{\epsilon }\frac{r}{a}\right){\left(2\sqrt{\epsilon }\frac{r}{a}\right)}^l{L}_{n-l-1}^{2l+1}\left(2\sqrt{\epsilon }\frac{r}{a}\right),\{\begin{array}{l}a=\frac{2\pi {\epsilon }_0{\hslash }^2}{m_e{e}^2}=\frac{a_0}{2}\\ \epsilon =-\frac{2m_e{a}^2}{{\hslash }^2}E\end{array}\\ =A·\exp \left(-\frac{r}{2na}\right){\left(\frac{r}{na}\right)}^l{L}_{n-l-1}^{2l+1}\left(\frac{r}{na}\right)\{\begin{array}{l}n=\mathrm{1,2,3...}\\ l=\mathrm{0,1,2...}n-1\\ m=-l\mathrm{,...0...}l\end{array}\end{array}}$

Es conveniente expresar R(r) en términos del cociente r/a₀ en vez de r/a, donde a₀ es el radio de Bohr

${\displaystyle R_{n,l}(r)=A·\exp \left(-\frac{r}{n{a}_0}\right){\left(\frac{2r}{n{a}_0}\right)}^l{L}_{n-l-1}^{2l+1}\left(\frac{2r}{n{a}_0}\right)}$

El coeficiente A se determina haciendo que

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}{r}^2}{R}_{n,l}^2(r)·dr=1}$

El volumen de una capa esférica comprendida entre r y r+dr es 4πr²·dr

Aunque existe una fórmula para el coeficiente A para cualquier n y l al igual que para los armónicos esféricos, esta es muy complicada de obtener, por lo que calcularemos la integral con la ayuda de MATLAB

Calculamos las primeras funciones R_m,l(r)

${\displaystyle \begin{array}{l}{R}_{\mathrm{1,0}}(r)=A\exp \left(-\frac{r}{a_0}\right)L_0^1\left(\frac{2r}{a_0}\right)=A\exp \left(-\frac{r}{a_0}\right)\\ {\displaystyle \underset{0}{\overset{\infty }{\int }}{r}^2}{R}_{\mathrm{1,0}}^2(r)·dr=1\\ A^2{\displaystyle \underset{0}{\overset{\infty }{\int }}{r}^2}\exp \left(-\frac{2r}{a_0}\right)·dr=\mathrm{1,}{A}^2\frac{a_0^3}{4}=1\\ R_{\mathrm{1,0}}(r)=\frac{2}{a_0^{3/2}}\exp \left(-\frac{r}{a_0}\right)\end{array}}$

>> syms a x;
>> assume(a,'positive')
>> int(x^2*exp(-2*x/a),x,0,inf)
 ans =a^3/4

${\displaystyle \begin{array}{l}{R}_{\mathrm{2,0}}(r)=A\exp \left(-\frac{r}{2a_0}\right)L_1^1\left(\frac{r}{a_0}\right)=A\exp \left(-\frac{r}{2a_0}\right)·\left(2-\frac{r}{a_0}\right)\\ A^2{\displaystyle \underset{0}{\overset{\infty }{\int }}{r}^2}{\left(2-\frac{r}{a_0}\right)}^2\exp \left(-\frac{r}{a_0}\right)·dr=\mathrm{1,}{A}^2·8a_0^3=1\\ R_{\mathrm{2,0}}(r)=\frac{1}{2\sqrt{2}{a}_0^{3/2}}\left(2-\frac{r}{a_0}\right)\exp \left(-\frac{r}{2a_0}\right)\end{array}}$

>> int(x^2*exp(-x/a)*(2-x/a)^2,x,0,inf)
 ans =8*a^3

${\displaystyle \begin{array}{l}{R}_{\mathrm{2,1}}(r)=A\exp \left(-\frac{r}{2a_0}\right)\left(\frac{r}{a_0}\right)·L_0^3\left(\frac{r}{a_0}\right)=A\exp \left(-\frac{r}{2a_0}\right)·\left(\frac{r}{a_0}\right)\\ A^2{\displaystyle \underset{0}{\overset{\infty }{\int }}{r}^2}{\left(\frac{r}{a_0}\right)}^2\exp \left(-\frac{r}{a_0}\right)·dr=\mathrm{1,}{A}^2·24a_0^3=1\\ R_{\mathrm{2,1}}(r)=\frac{1}{2\sqrt{6}{a}_0^{3/2}}\frac{r}{a_0}\exp \left(-\frac{r}{2a_0}\right)\end{array}}$

>> int(x^2*exp(-x/a)*(x/a)^2,x,0,inf)
 ans =24*a^3

${\displaystyle \begin{array}{l}{R}_{\mathrm{3,0}}(r)=A\exp \left(-\frac{r}{3a_0}\right)·L_2^1\left(\frac{2r}{3a_0}\right)=A\exp \left(-\frac{r}{3a_0}\right)·\left(\frac{1}{2}{\left(\frac{2r}{3a_0}\right)}^2-3\frac{2r}{3a_0}+3\right)\\ A^2{\displaystyle \underset{0}{\overset{\infty }{\int }}{r}^2}{\left(\frac{2}{9}{\left(\frac{r}{a_0}\right)}^2-2\frac{r}{a_0}+3\right)}^2\exp \left(-\frac{2r}{3a_0}\right)·dr=\mathrm{1,}{A}^2\frac{243}{4}{a}_0^3=1\\ R_{\mathrm{3,0}}(r)=\frac{2}{81\sqrt{3}{a}_0^{3/2}}\left(2{\left(\frac{r}{a_0}\right)}^2-18\frac{r}{a_0}+27\right)\exp \left(-\frac{r}{3a_0}\right)\end{array}}$

>> int(x^2*exp(-2*x/(3*a))*(2*(x/a)^2/9-2*(x/a)+3)^2,x,0,inf)
 ans =(243*a^3)/4

${\displaystyle \begin{array}{l}{R}_{\mathrm{3,1}}(r)=A\exp \left(-\frac{r}{3a_0}\right)·\left(\frac{2r}{3a_0}\right)·L_1^3\left(\frac{2r}{3a_0}\right)=A\exp \left(-\frac{r}{3a_0}\right)\left(\frac{2r}{3a_0}\right)·\left(-\frac{2r}{3a_0}+4\right)\\ A^2{\displaystyle \underset{0}{\overset{\infty }{\int }}{r}^2}{\left(\frac{2r}{3a_0}\right)}^2{\left(-\frac{2r}{3a_0}+4\right)}^2\exp \left(-\frac{2r}{3a_0}\right)·dr=\mathrm{1,}{A}^2·486·a_0^3=1\\ R_{\mathrm{3,1}}(r)=\frac{4}{81\sqrt{6}{a}_0^{3/2}}\left(6-\frac{r}{a_0}\right)\frac{r}{a_0}\exp \left(-\frac{r}{3a_0}\right)\end{array}}$

>> int(x^2*exp(-2*x/(3*a))*(2*x/(3*a))^2*(-2*x/(3*a)+4)^2,x,0,inf)
 ans =486*a^3

${\displaystyle \begin{array}{l}{R}_{\mathrm{3,2}}(r)=A\exp \left(-\frac{r}{3a_0}\right)·{\left(\frac{2r}{3a_0}\right)}^2·L_0^5\left(\frac{2r}{3a_0}\right)=A\exp \left(-\frac{r}{3a_0}\right)·{\left(\frac{2r}{3a_0}\right)}^2\\ A^2{\displaystyle \underset{0}{\overset{\infty }{\int }}{r}^2}{\left(\frac{2r}{3a_0}\right)}^4\exp \left(-\frac{2r}{3a_0}\right)·dr=\mathrm{1,}{A}^2·2430·a_0^3=1\\ R_{\mathrm{3,2}}(r)=\frac{4}{81\sqrt{30}{a}_0^{3/2}}{\left(\frac{r}{a_0}\right)}^2\exp \left(-\frac{r}{3a_0}\right)\end{array}}$

>> int(x^2*exp(-2*x/(3*a))*(2*x/(3*a))^4,x,0,inf)
 ans =2430*a^3

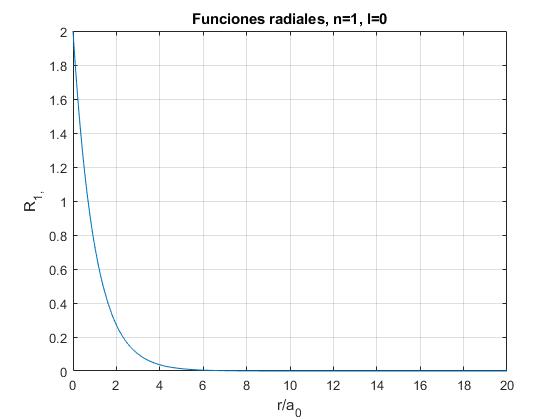
Representamos las primeras funciones $R_{n,l}(r)·a_0^{3/2}$, en función del cociente r/a₀

f=@(x) 2*exp(-x);
fplot(f,[0,20])
grid on
xlabel('r/a_0')
ylabel('R_{1,}')
title('Funciones radiales, n=1, l=0')
 
figure
f1=@(x) (2-x).*exp(-x/2)/(2*sqrt(2));
f2=@(x) x.*exp(-x/2)/(2*sqrt(6));
hold on
fplot(f1,[0,20])
fplot(f2,[0,20])
hold off
grid on
xlabel('r/a_0')
ylabel('R_{2,}')
legend('R_{2,0}', 'R_{2,1}')
title('Funciones radiales, n=2, l=0 y l=1')
 
figure
f1=@(x) (2*x.^2-18*x+27).*exp(-x/3)*2/(81*sqrt(3));
f2=@(x) (6-x).*x.*exp(-x/3)*4/(81*sqrt(6));
f3=@(x) (x.^2).*exp(-x/3)*4/(81*sqrt(30));
hold on
fplot(f1,[0,20])
fplot(f2,[0,20])
fplot(f3,[0,20])
hold off
grid on
xlabel('r/a_0')
ylabel('R_{3,}')
legend('R_{3,0}', 'R_{3,1}', 'R_{3,2}')
title('Funciones radiales, n=3, l=0, l=1 y l=2')

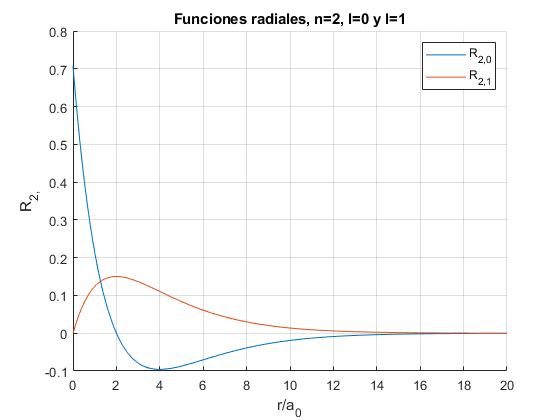
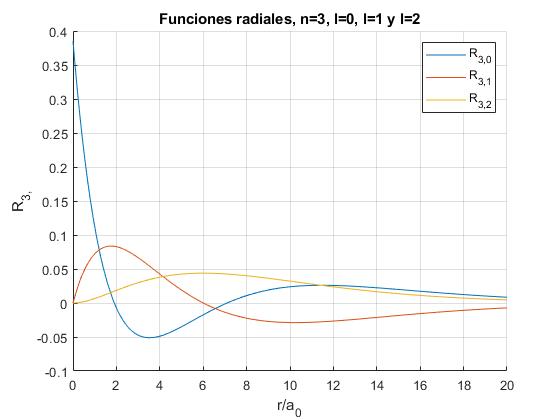
Combinando la solución radial y angular

En general

${\displaystyle {\psi }_{n,l,m}(r,\theta ,\phi )=R_{n,l}(r)Y_{l,m}(\theta ,\phi ),\{\begin{array}{l}n=\mathrm{1,2,3...}\\ l=\mathrm{0,1,2...}n-1\\ m=-l\mathrm{,...0...}l\end{array}}$

Para cada valor de n que especifica un nivel de energía, hay n valores diferentes del momento angular, desde l=0 hasta l=n-1. El número cuántico l está relacionado con el módulo del momento angular L

Al resolver la ecuación diferencial de la parte angular, ya se ha especificado los posibles valores de m=0, ±1, ±2, ±3,... ±l. El número cuántico m está relacionado con la componente L_z, es decir, la dirección del momento angular

Las primeras funciones son

${\displaystyle \begin{array}{l}{\psi }_{\mathrm{1,0,0}}(r,\theta ,\phi )=R_{\mathrm{1,0}}(r)Y_{\mathrm{0,0}}(\theta ,\phi )=\frac{1}{\sqrt{\pi }{a}_0^{3/2}}\exp \left(-\frac{r}{a_0}\right)\\ {\psi }_{\mathrm{2,0,0}}(r,\theta ,\phi )=R_{\mathrm{2,0}}(r)Y_{\mathrm{0,0}}(\theta ,\phi )=\frac{1}{4\sqrt{2\pi }{a}_0^{3/2}}\left(2-\frac{r}{a_0}\right)\exp \left(-\frac{r}{2a_0}\right)\\ {\psi }_{\mathrm{2,1,0}}(r,\theta ,\phi )=R_{\mathrm{2,1}}(r)Y_{\mathrm{1,0}}(\theta ,\phi )=\frac{1}{4\sqrt{2\pi }{a}_0^{3/2}}\frac{r}{a_0}\exp \left(-\frac{r}{2a_0}\right)\cos \theta \\ {\psi }_{\mathrm{2,1,}\pm 1}(r,\theta ,\phi )=R_{\mathrm{2,1}}(r)Y_{\mathrm{1,}\pm 1}(\theta ,\phi )=\frac{1}{8\sqrt{\pi }{a}_0^{3/2}}\frac{r}{a_0}\exp \left(-\frac{r}{2a_0}\right)\sin \theta ·e^{\pm i\phi }\\ {\psi }_{\mathrm{3,0,0}}(r,\theta ,\phi )=R_{\mathrm{3,0}}(r)Y_{\mathrm{0,0}}(\theta ,\phi )=\frac{2}{81\sqrt{3\pi }{a}_0^{3/2}}\left(2{\left(\frac{r}{a_0}\right)}^2-18\frac{r}{a_0}+27\right)\exp \left(-\frac{r}{3a_0}\right)\\ {\psi }_{\mathrm{3,1,0}}(r,\theta ,\phi )=R_{\mathrm{3,1}}(r)Y_{\mathrm{1,0}}(\theta ,\phi )=\frac{\sqrt{2}}{81\sqrt{\pi }{a}_0^{3/2}}\left(6-\frac{r}{a_0}\right)\frac{r}{a_0}\exp \left(-\frac{r}{3a_0}\right)\cos \theta \\ {\psi }_{\mathrm{3,1,}\pm 1}(r,\theta ,\phi )=R_{\mathrm{3,1}}(r)Y_{\mathrm{1,}\pm 1}(\theta ,\phi )=\frac{1}{81\sqrt{\pi }{a}_0^{3/2}}\left(6-\frac{r}{a_0}\right)\frac{r}{a_0}\exp \left(-\frac{r}{3a_0}\right)\sin \theta ·e^{\pm i\phi }\\ {\psi }_{\mathrm{3,2,0}}(r,\theta ,\phi )=R_{\mathrm{3,2}}(r)Y_{\mathrm{2,0}}(\theta ,\phi )=\frac{1}{81\sqrt{6\pi }{a}_0^{3/2}}{\left(\frac{r}{a_0}\right)}^2\exp \left(-\frac{r}{3a_0}\right)(3{\cos }^2\theta -1)\\ {\psi }_{\mathrm{3,2,}\pm 1}(r,\theta ,\phi )=R_{\mathrm{3,2}}(r)Y_{\mathrm{2,}\pm 1}(\theta ,\phi )=\frac{1}{81\sqrt{\pi }{a}_0^{3/2}}{\left(\frac{r}{a_0}\right)}^2\exp \left(-\frac{r}{3a_0}\right)\cos \theta ·\sin \theta ·e^{\pm i\phi }\end{array}}$

Estas funciones cumplen

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{\pi }{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{\left|{\psi }_{n,l,m}(r,\theta ,\phi )\right|}^2{r}^2\sin \theta ·d\theta ·d\phi =1}}}}$

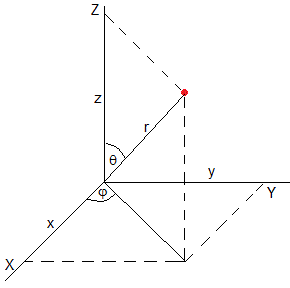
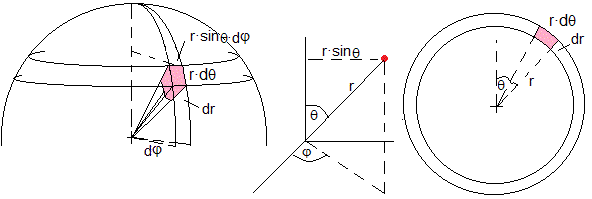
En la figura, el elemento de volumen dV=dr·rdθ·(rsinθ·dφ)=r²sinθ·dφ·dθ en coordenadas esféricas, el ángulo φ varía entre 0 y 2π, el ángulo θ, entre 0 y π

Referencias

Blomm D., Blomm D. W. Vibrating wire loop and the Bohr model. The Physics Teacher, 41, May 2003, pp. 292-294

R. L. Herman. The Three-dimensional Schödinger Equation. November 7, 2016