La ecuación de Schrödinger en coordenadas cilíndricas para una partícula de masa m en un potencial V(ρ, φ, z) es

${\displaystyle -\frac{{\hslash }^2}{2m}\left(\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial \psi (\rho ,\phi ,z)}{\partial \rho }\right)+\frac{1}{{\rho }^2}\frac{{\partial }^2\psi (\rho ,\phi ,z)}{\partial {\phi }^2}+\frac{{\partial }^2\psi (\rho ,\phi ,z)}{\partial z^2}\right)+V(\rho ,\phi ,z)\psi (\rho ,\phi ,z)=E\psi (\rho ,\phi ,z)}$

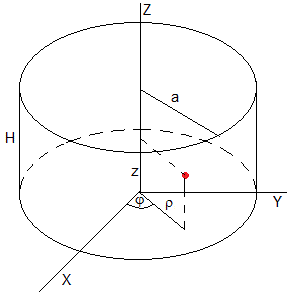
Una partícula se mueve en un recinto de forma cilíndica de radio a y altura H, el potencial es

${\displaystyle V(\rho ,z)=\{\begin{array}{l}\mathrm{0,}0\le \rho \le a,0\le z\le H\\ \infty ,z<\mathrm{0,}z>H\text{y}\rho >a\end{array}}$

La función de onda es nula en la superficie del recinto, en su interior la ecuación de Schrödinger es

${\displaystyle -\frac{{\hslash }^2}{2m}\left(\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial \psi (\rho ,\phi ,z)}{\partial \rho }\right)+\frac{1}{{\rho }^2}\frac{{\partial }^2\psi (\rho ,\phi ,z)}{\partial {\phi }^2}+\frac{{\partial }^2\psi (\rho ,\phi ,z)}{\partial z^2}\right)=E\psi (\rho ,\phi ,z)}$

Variables separadas

Probamos la solución $\psi (\rho ,\phi ,z)={\psi }_{\rho \phi }(\rho ,\phi )·Z(z)$ , variables separadas.

${\displaystyle \begin{array}{l}\left(\frac{Z}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial {\psi }_{\rho \phi }}{\partial \rho }\right)+\frac{Z}{{\rho }^2}\frac{{\partial }^2{\psi }_{\rho \phi }}{\partial {\phi }^2}+{\psi }_{\rho \phi }\frac{d^{2}Z}{d{z}^2}\right)=-\frac{2mE}{{\hslash }^2}{\psi }_{\rho \phi }Z\\ \frac{1}{{\psi }_{\rho \phi }}\left(\frac{1}{\rho }\frac{\partial {\psi }_{\rho \phi }}{\partial \rho }+\frac{{\partial }^2{\psi }_{\rho \phi }}{\partial {\rho }^2}+\frac{1}{{\rho }^2}\frac{{\partial }^2{\psi }_{\rho \phi }}{\partial {\phi }^2}\right)+\frac{1}{Z}\frac{d^{2}Z}{d{z}^2}=-\frac{2mE}{{\hslash }^2}\end{array}}$

El primer término depende de ρ y φ, el segundo solamente de z

La ecuación diferencial se transforma en el sistema de dos ecuaciones diferenciales de variables separadas

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{1}{\rho }\frac{\partial {\psi }_{\rho \phi }}{\partial \rho }+\frac{{\partial }^2{\psi }_{\rho \phi }}{\partial {\rho }^2}+\frac{1}{{\rho }^2}\frac{{\partial }^2{\psi }_{\rho \phi }}{\partial {\phi }^2}=-k_{\rho \phi }^2{\psi }_{\rho \phi }\\ \frac{1}{Z}\frac{d^{2}Z}{d{z}^2}=-k_z^{2}Z\end{array}\\ k_{\rho \phi }^2+k_z^2=\frac{2mE}{{\hslash }^2}\end{array}}$

Transformamos la primera ecuación diferencial en un sistema de dos ecuaciones diferenciales en variables separadas ρ y φ

${\displaystyle \begin{array}{l}{\psi }_{\rho \phi }(\rho ,\phi )=R(\rho )F(\phi )\\ \frac{F}{\rho }\frac{dR}{d\rho }+F\frac{d^{2}R}{d{\rho }^2}+\frac{R}{{\rho }^2}\frac{d^{2}F}{d{\phi }^2}=-k_{\rho \phi }^{2}RF\\ \left(\frac{\rho }{R}\frac{dR}{d\rho }+\frac{{\rho }^2}{R}\frac{d^{2}R}{d{\rho }^2}+k_{\rho \phi }^2{\rho }^2\right)+\frac{1}{F}\frac{d^{2}F}{d{\phi }^2}=0\end{array}}$

El primer término, solamente depende de ρ, el segundo de φ, la ecuación diferencial se transforma en el sistema de dos ecuaciones diferenciales

${\displaystyle \{\begin{array}{l}\frac{\rho }{R}\frac{dR}{d\rho }+\frac{{\rho }^2}{R}\frac{d^{2}R}{d{\rho }^2}+k_{\rho \phi }^2{\rho }^2-n_{\phi }^2=0\\ \frac{1}{F}\frac{d^{2}F}{d{\phi }^2}=-n_{\phi }^2\end{array}}$

Hemos convertido ecuación de Schrödinger en coordenadas cilíndricas en un sistema de tres ecuaciones diferenciales en variables separadas ρ, φ y z

${\displaystyle \begin{array}{l}\{\begin{array}{l}{\rho }^2\frac{d^{2}R}{d{\rho }^2}+\rho \frac{dR}{d\rho }+\left(k_{\rho \phi }^2{\rho }^2-n_{\phi }^2\right)R=0\\ \frac{d^{2}F}{d{\phi }^2}=-n_{\phi }^{2}F\\ \frac{d^{2}Z}{d{z}^2}=-k_z^{2}Z\end{array}\\ k_{\rho \phi }^2+k_z^2=\frac{2mE}{{\hslash }^2}\end{array}}$

La ecuación radial

Haciendo el cambio de variable, x=ρk_ρφ, resolvemos la ecuación diferencial

${\displaystyle x^2\frac{d^{2}R}{d{x}^2}+x\frac{dR}{dx}+\left(x^2-n_{\phi }^2\right)R=0}$

La solución de esta ecuación diferencial es

${\displaystyle R(\rho )=A·J_{n_{\phi }}\left(k_{\rho \phi }\rho \right)+B·Y_{n_{\phi }}\left(k_{\rho \phi }\rho \right)}$

Ahora bien, hemos de descartar la función Y, ya que tiende a infinito cuando x→0

${\displaystyle R(\rho )=A·J_{n_{\phi }}\left(k_{\rho \phi }\rho \right)}$

En la superficie de la región cilíndrica, para ρ=a, la función de onda es nula, R(a)=0, lo que implica que

${\displaystyle J_{n_{\phi }}\left(k_{\rho \phi }a\right)=0}$

Denominamos ${\xi }_{n_{\phi },n_{\rho }}$ a las raíces de $J_{n_{\phi }}(x)=0$, por lo que el parámetro k_ρφ vale

${\displaystyle k_{\rho \phi }=\frac{{\xi }_{n_{\phi },n_{\rho }}}{a},n_{\rho }=\mathrm{1,2,3...}}$

n_ρ es el índice de la raíz

La ecuación angular

${\displaystyle \frac{d^{2}F}{d{\phi }^2}+n_{\phi }^{2}F=0}$

Tiene una solución conocida, que expresamos de forma equivalente

${\displaystyle F(\phi )=C_1\exp \left(i{n}_{\phi }\phi \right)+C_2\exp \left(-i{n}_{\phi }\phi \right)}$

La solución es periódica, F(φ+2π)=F(φ). Igualando las partes real e imaginaria

${\displaystyle \begin{array}{l}\{\begin{array}{l}{C}_1\cos \left(n_{\phi }\phi +2\pi n_{\phi }\right)+C_2\cos \left(n_{\phi }\phi +2\pi n_{\phi }\right)=C_1\cos \left(n_{\phi }\phi \right)+C_2\cos \left(n_{\phi }\phi \right)\\ C_1\sin \left(n_{\phi }\phi +2\pi n_{\phi }\right)-C_2\sin \left(n_{\phi }\phi +2\pi n_{\phi }\right)=C_1\sin \left(n_{\phi }\phi \right)-C_2\sin \left(n_{\phi }\phi \right)\end{array}\\ \{\begin{array}{l}\left(C_1+C_2\right)\cos \left(n_{\phi }\phi +2\pi n_{\phi }\right)=\left(C_1+C_2\right)\cos \left(n_{\phi }\phi \right)\\ \left(C_1-C_2\right)\sin \left(n_{\phi }\phi +2\pi n_{\phi }\right)=\left(C_1-C_2\right)\sin \left(n_{\phi }\phi \right)\end{array}\end{array}}$

Si C₁≠C₂ y C₁+ C₂≠0, entonces n_φ tiene que ser un entero.

${\displaystyle F(\phi )=C\exp (i{n}_{\phi }\phi ),n_{\phi }=\mathrm{0,}\pm \mathrm{1,}\pm \mathrm{2....}}$

Ecuación a lo largo de la dirección Z

${\displaystyle \frac{d^{2}Z}{d{z}^2}+k_z^{2}Z=0}$

La solución de esta ecuación diferencial es conocida

${\displaystyle Z(z)=D_1\cos \left(k_{z}z\right)+D_2\sin \left(k_{z}z\right)}$

La función de onda se anula en los bordes de la región cilíndrica

• Para z=0, Z(0)=0

Lo que implica que D₁=0

${\displaystyle Z(z)=D_2\sin \left(k_{z}z\right)}$

• Para z=H, Z(H)=0

Lo que implica que k_zH=n_zπ, n_z=1, 2, 3,..

La expresión de Z(z) es

${\displaystyle Z(z)=D_2\sin \left(n_z\pi \frac{z}{H}\right)}$

Niveles de energía

La energía E de los niveles es

${\displaystyle E=\frac{{\hslash }^2}{2m}\left(k_{\rho \phi }^2+k_z^2\right)=\frac{{\hslash }^2}{2m}\left({\left(\frac{{\xi }_{n_{\phi },n_{\rho }}}{a}\right)}^2+{\left(\frac{n_z\pi }{H}\right)}^2\right),\{\begin{array}{l}{n}_{\phi }=\mathrm{0,1,2,3...}\\ n_{\rho }=\mathrm{1,2,3...}\\ n_z=\mathrm{1,2,3...}\end{array}}$

Función de onda

${\displaystyle \psi (\rho ,\phi ,z)={\psi }_{\rho \phi }(\rho ,\phi )·Z(z)=R(\rho )·F(\phi )·Z(z)}$

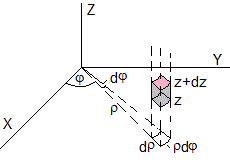
El elemento diferencial de volumen en coordenadas cilíndricas es

${\displaystyle dV=d\rho \left(\rho ·d\phi \right)dz}$

La función de onda ha de cumplir

${\displaystyle \begin{array}{l}{\displaystyle \underset{V}{\int }{\displaystyle \int {\displaystyle \int \psi (\rho ,\phi ,z)}}·{\psi }^{*}(\rho ,\phi ,z)·\left(\rho ·d\rho ·d\phi ·dz\right)=}\\ \left({\displaystyle \underset{0}{\overset{a}{\int }}\rho ·R(\rho )R^{*}(\rho )d\rho }\right)\left({\displaystyle \underset{0}{\overset{2\pi }{\int }}F(\phi )F^{*}(\phi )·d\phi }\right)\left({\displaystyle \underset{0}{\overset{H}{\int }}Z(z)Z^{*}(z)·dz}\right)=1\end{array}}$

• La parte radial de la función de onda R(ρ)

${\displaystyle {\displaystyle \underset{0}{\overset{a}{\int }}\rho ·R(\rho )R^{*}(\rho )d\rho }=A^2{\displaystyle \underset{0}{\overset{a}{\int }}\rho ·J_{n_{\phi }}^2\left(k_{\rho \phi }\rho \right)·d\rho }=1}$

Teniendo en cuenta las relaciones de ortogonalidad

${\displaystyle {\displaystyle \underset{0}{\overset{1}{\int }}x{J}_n(k_{m}x)J_n(k_{l}x)dx}=\{\begin{array}{l}\mathrm{0,}m\ne l\\ \frac{1}{2}{J}_{n+1}^2(k_m),m=l\end{array}}$

y haciendo el cambio de variable, x=ρ/a, dx=dρ/a

${\displaystyle \begin{array}{l}{A}^2{a}^2{\displaystyle \underset{0}{\overset{1}{\int }}x·J_{n_{\phi }}^2\left(k_{\rho \phi }ax\right)·dx}=1\\ A^2{a}^2\frac{1}{2}{J}_{n_{\phi }+1}^2\left(k_{\rho \phi }a\right)=1\end{array}}$

La parte radial de la función de onda es

${\displaystyle R_{n_{\rho }{n}_{\phi }}(\rho )=\frac{\sqrt{2}}{a·J_{n_{\phi }+1}\left({\xi }_{n_{\phi },n_{\rho }}\right)}·J_{n_{\phi }}\left({\xi }_{n_{\phi },n_{\rho }}\frac{\rho }{a}\right)}$

donde ${\xi }_{n_{\phi },n_{\rho }}$, es la raíz n_ρ de la función $J_{n_{\phi }}(x)=0$

• La parte angular de la función de onda

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{2\pi }{\int }}F(\phi )F^{*}(\phi )·d\phi }=1\\ C^2{\displaystyle \underset{0}{\overset{2\pi }{\int }}\exp \left(i{n}_{\phi }\phi \right)·\exp \left(-i{n}_{\phi }\phi \right)d\phi }=1\\ C^2·2\pi =1\end{array}}$

La parte angular de la función de onda

${\displaystyle F(\phi )=\frac{1}{\sqrt{2\pi }}\exp (i{n}_{\phi }\phi )}$

• La parte de la función de onda a lo largo del eje Z

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{H}{\int }}Z(z)Z^{*}(z)·dz}=1\\ {\displaystyle \underset{0}{\overset{H}{\int }}{D}_2\sin \left(n_z\pi \frac{z}{H}\right)D_2^{*}\sin \left(n_z\pi \frac{z}{H}\right)·dz}=1\\ D_2^2{\displaystyle \underset{0}{\overset{H}{\int }}{\sin }^2\left(n_z\pi \frac{z}{H}\right)·dz}=1\\ D_2^2{\displaystyle \underset{0}{\overset{H}{\int }}\frac{1-\cos \left(2n_z\pi \frac{z}{H}\right)}{2}·dz=1}\\ \frac{D_2^2}{2}H=1\end{array}}$

La parte de la función de onda a lo largo del eje Z es

${\displaystyle Z(z)=\sqrt{\frac{2}{H}}\sin \left(n_z\pi \frac{z}{H}\right)}$

Función de onda es

${\displaystyle {\psi }_{n_{\rho },n_{\phi },n_z}(\rho ,\phi ,z)=\frac{1}{J_{n_{\phi }+1}\left({\xi }_{n_{\phi },n_{\rho }}\right)}·\sqrt{\frac{2}{\pi H{a}^2}}·J_{n_{\phi }}\left({\xi }_{n_{\phi },n_{\rho }}\frac{\rho }{a}\right)\sin \left(n_z\pi \frac{z}{H}\right)\exp \left(i{n}_{\phi }\phi \right)\{\begin{array}{l}{n}_{\phi }=\mathrm{0,1,2,3...}\\ n_{\rho }=\mathrm{1,2,3...}\\ n_z=\mathrm{1,2,3...}\end{array}}$

Los niveles de energía dependen de tres números enteros asociados a tres direcciones n_ρ, n_φ y n_z. La función de onda depende de dichos números y de un valor extra p=±n_φ

Representamos gráficamente la parte radial de la función de onda $a{R}_{n_{\rho }{n}_{\phi }}(\rho )$ en función de ρ/a, para

• n_φ=0, n_ρ=1,2,3
• n_φ=1, n_ρ=1,2,3

hold on
np=0;
for nr=1:3
    r0=(2*nr-1)*pi/2+np*pi/2+pi/4; %ceros coseno
    xi=fzero(@(x) besselj(np,x), r0); %raíz
    disp(xi)
    f=@(x) sqrt(2)*besselj(np,x*xi)/besselj(np+1,xi);
    fplot(f,[0,1])
end
hold off
xlabel('\rho/a')
ylabel('aR')
legend('R_{1,0}','R_{2,0}','R_{3,0}','Location','best')
grid on
title('Componente radial')

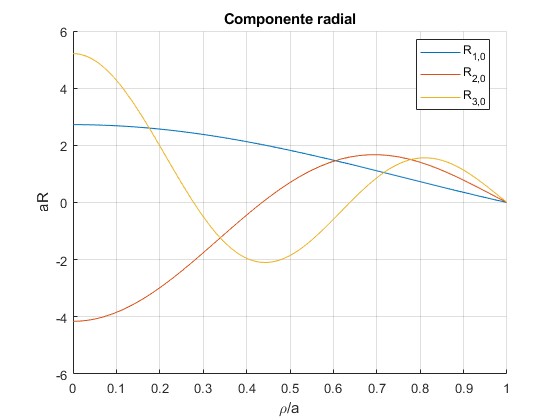
Los valores de k_ρφ para n_φ=0, las raíces de J₀(x), son

    2.4048
    5.5201
    8.6537

Cambiamos n_φ=1

hold on
np=1;
for nr=1:3
    r0=(2*nr-1)*pi/2+np*pi/2+pi/4; %ceros coseno
    xi=fzero(@(x) besselj(np,x), r0); %raíz
    disp(xi)
    f=@(x) sqrt(2)*besselj(np,x*xi)/besselj(np+1,xi);
    fplot(f,[0,1])
end
hold off
xlabel('\rho/a')
ylabel('aR')
legend('R_{1,1}','R_{2,1}','R_{3,1}','Location','best')
grid on
title('Componente radial')

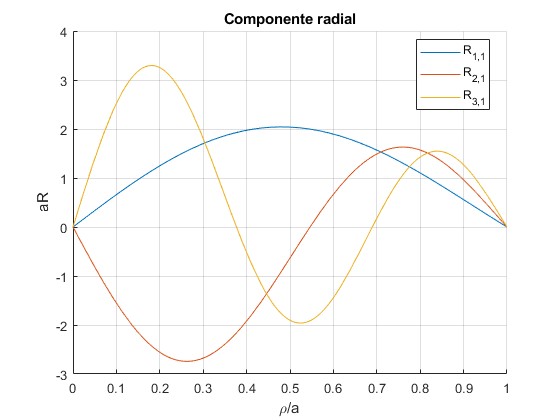
Los valores de k_ρφ para n_φ=1, las raíces de J₁(x) son

    3.8317
    7.0156
   10.1735

Pozo de potencial circular de altura infinita

Una partícula de masa m se mueve en un recinto de forma circular de radio a. El potencial es

${\displaystyle V(\rho )=\{\begin{array}{l}\mathrm{0,}0\le \rho <a\\ \infty ,\rho \ge a\end{array}}$

Buscamos la solución de la ecuación de Schrödinger en coordenadas cilíndricas independiente de la altura z

${\displaystyle -\frac{{\hslash }^2}{2m}\left(\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial \psi (\rho ,\phi )}{\partial \rho }\right)+\frac{1}{{\rho }^2}\frac{{\partial }^2\psi (\rho ,\phi )}{\partial {\phi }^2}\right)+V(\rho )\psi (\rho ,\phi )=E\psi (\rho ,\phi )}$

Aplicamos el procedimiento de sepación de variables

${\displaystyle \begin{array}{l}{\psi }_{\rho \phi }(\rho ,\phi )=R(\rho )F(\phi )\\ \frac{F}{\rho }\frac{dR}{d\rho }+F\frac{d^{2}R}{d{\rho }^2}+\frac{R}{{\rho }^2}\frac{d^{2}F}{d{\phi }^2}=-\frac{2mE}{{\hslash }^2}RF\\ \left(\frac{\rho }{R}\frac{dR}{d\rho }+\frac{{\rho }^2}{R}\frac{d^{2}R}{d{\rho }^2}+k^2{\rho }^2\right)+\frac{1}{F}\frac{d^{2}F}{d{\phi }^2}=0\\ k^2=\frac{2mE}{{\hslash }^2}\end{array}}$

El primer término, solamente depende de ρ, el segundo de φ, la ecuación diferencial se transforma en el sistema de dos ecuaciones diferenciales

${\displaystyle \{\begin{array}{l}\rho \frac{dR}{d\rho }+{\rho }^2\frac{d^{2}R}{d{\rho }^2}+\left(k^2{\rho }^2-n_{\phi }^2\right)R=0\\ \frac{d^{2}F}{d{\phi }^2}=-n_{\phi }^{2}F\end{array}}$

La ecuación radial

Haciendo el cambio de variable, x=ρk_ρφ, resolvemos la ecuación diferencial

${\displaystyle x^2\frac{d^{2}R}{d{x}^2}+x\frac{dR}{dx}+\left(x^2-n_{\phi }^2\right)R=0}$

La solución de esta ecuación diferencial es

${\displaystyle R(\rho )=A·J_{n_{\phi }}\left(k\rho \right)+B·Y_{n_{\phi }}\left(k\rho \right)}$

Ahora bien, hemos de descartar la función Y, ya que tiende a infinito cuando x→0

${\displaystyle R(\rho )=A·J_{n_{\phi }}\left(k\rho \right)}$

Para ρ=a, la función de onda es nula, R(a)=0, lo que implica que

${\displaystyle J_{n_{\phi }}\left(ka\right)=0}$

Denominamos ${\xi }_{n_{\phi },n_{\rho }}$ a las raíces de $J_{n_{\phi }}(x)=0$, por lo que el parámetro k vale

${\displaystyle k=\frac{{\xi }_{n_{\phi },n_{\rho }}}{a},n_{\rho }=\mathrm{1,2,3...}}$

n_ρ es el índice de la raíz

La ecuación angular

${\displaystyle \frac{d^{2}F}{d{\phi }^2}+n_{\phi }^{2}F=0}$

La misma solución que en el primer apartado

Niveles de energía

La energía E de los niveles es

${\displaystyle E_{n_{\phi },n_{\rho }}=\frac{{\hslash }^2}{2m{a}^2}{\xi }_{n_{\phi },n_{\rho }}^2}$

Función de onda

Es el producto de las dos soluciones

${\displaystyle \psi (\rho ,\phi )=R(\rho )·F(\phi )}$

La función de onda ha de cumplir

${\displaystyle \begin{array}{l}{\displaystyle \int {\displaystyle \int \psi (\rho ,\phi )}}·{\psi }^{*}(\rho ,\phi )·\left(\rho ·d\rho ·d\phi \right)=\\ \left({\displaystyle \underset{0}{\overset{a}{\int }}\rho ·R(\rho )R^{*}(\rho )d\rho }\right)\left({\displaystyle \underset{0}{\overset{2\pi }{\int }}F(\phi )F^{*}(\phi )·d\phi }\right)=1\end{array}}$

Repitiendo los mismos cálculos que en el apartado anterior

• La parte radial de la función de onda es

${\displaystyle R_{n_{\rho }{n}_{\phi }}(\rho )=\frac{\sqrt{2}}{a·J_{n_{\phi }+1}\left({\xi }_{n_{\phi },n_{\rho }}\right)}·J_{n_{\phi }}\left({\xi }_{n_{\phi },n_{\rho }}\frac{\rho }{a}\right)}$

donde ${\xi }_{n_{\phi },n_{\rho }}$, es la raíz n_ρ de la función $J_{n_{\phi }}(x)=0$

• La parte angular de la función de onda

${\displaystyle F(\phi )=\frac{1}{\sqrt{2\pi }}\exp (i{n}_{\phi }\phi )}$

La parte real de la función de onda es

${\displaystyle {\psi }_{n_{\rho },n_{\phi }}(\rho ,\phi )=\frac{1}{J_{n_{\phi }+1}\left({\xi }_{n_{\phi },n_{\rho }}\right)}·\sqrt{\frac{1}{\pi a^2}}·J_{n_{\phi }}\left({\xi }_{n_{\phi },n_{\rho }}\frac{\rho }{a}\right)\cos \left(n_{\phi }\phi \right)\{\begin{array}{l}{n}_{\phi }=\mathrm{0,1,2,3...}\\ n_{\rho }=\mathrm{1,2,3...}\end{array}}$

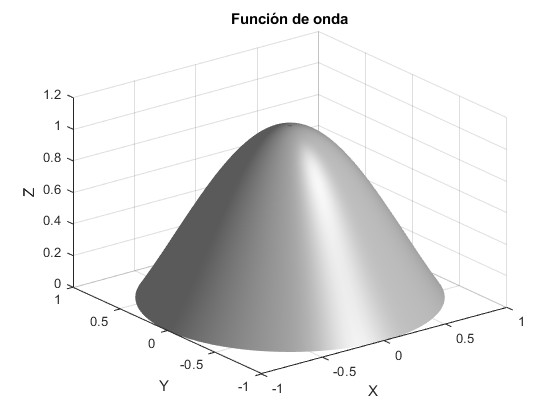
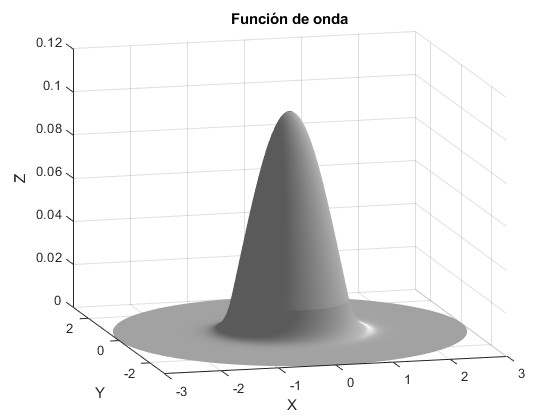
Representamos la función de onda para algunos valores de n_φ y n_ρ

np=0;
nr=1;
r0=(2*nr-1)*pi/2+np*pi/2+pi/4; %ceros coseno
xi=fzero(@(x) besselj(np,x), r0); %raíz
disp(xi)
rho=linspace(0,1,50);
phi=linspace(0,2*pi, 100);
[Rho,Phi]=meshgrid(rho,phi);
X=Rho.*cos(Phi);
Y=Rho.*sin(Phi);
Z=cos(np*Phi).*besselj(np,Rho*xi)/(sqrt(pi)*besselj(np+1,xi));
surfl(X,Y,Z)
shading interp
colormap(gray);
text(-0.9,1,2,num2str(xi^2))
xlabel('X')
ylabel('Y')
zlabel('Z')
grid on
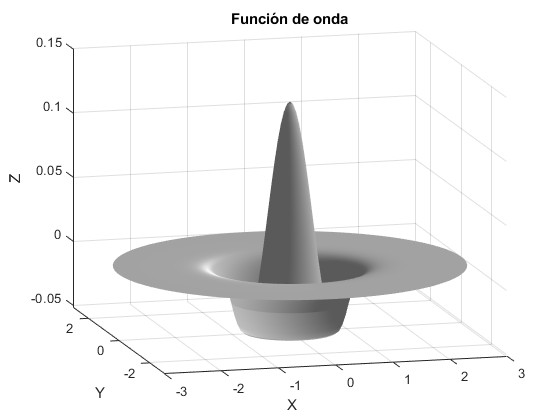
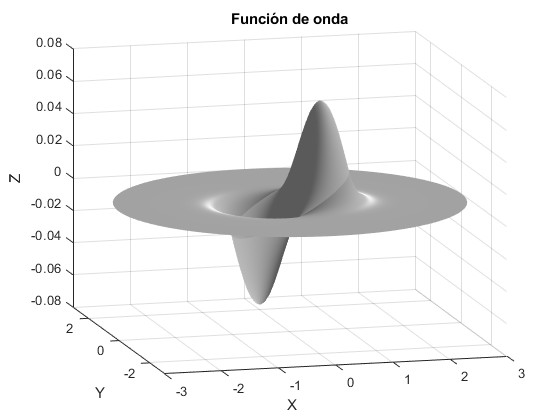
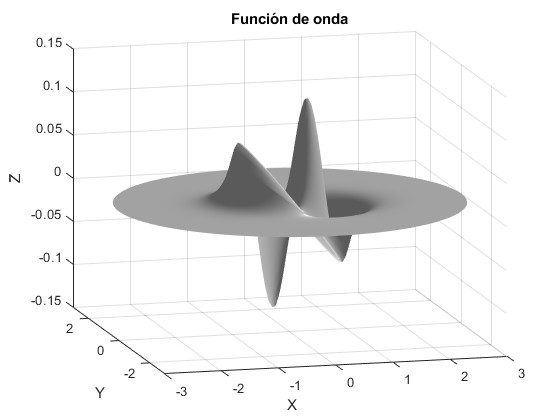
title('Función de onda')

• n_φ=0, n_ρ=1. La primera raíz de la función J₀(x) es 2.4048. Elevando al cuadrado obtenemos la energía en unidades ħ²/2ma²



• n_φ=0, n_ρ=2. La segunda raíz de la función J₀(x) es 5.5201



• n_φ=1, n_ρ=1. La primera raíz de la función J₁(x) es 3.8317



• n_φ=1, n_ρ=2. La segunda raíz de la función J₁(x) es 7.0156

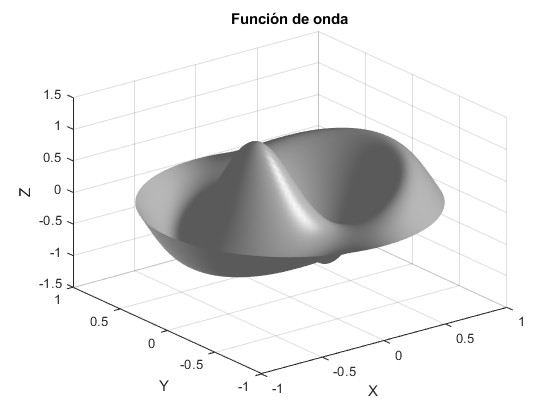
Pozo de potencial circular de altura finita

Una partícula de masa m se mueve en un recinto de forma circular de radio a. El potencial es

${\displaystyle V(\rho ,\phi )=\{\begin{array}{l}-V_0,0\le \rho \le a\\ \mathrm{0,}\rho >a\end{array}}$

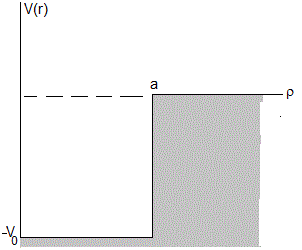
Buscamos la solución de la ecuación de Schrödinger en coordenadas cilíndricas independiente de la altura z

${\displaystyle -\frac{{\hslash }^2}{2m}\left(\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial \psi (\rho ,\phi )}{\partial \rho }\right)+\frac{1}{{\rho }^2}\frac{{\partial }^2\psi (\rho ,\phi )}{\partial {\phi }^2}\right)+V(\rho )\psi (\rho ,\phi )=E\psi (\rho ,\phi )}$

Aplicamos el procedimiento de sepación de variables

${\displaystyle \begin{array}{l}\psi (\rho ,\phi )=R(\rho )·F(\phi )\\ \frac{F}{\rho }\frac{dR}{d\rho }+F\frac{d^{2}R}{d{\rho }^2}+\frac{R}{{\rho }^2}\frac{d^{2}F}{d{\phi }^2}=-\frac{2m}{{\hslash }^2}\left(E-V(\rho )\right)RF\\ \left(\frac{\rho }{R}\frac{dR}{d\rho }+\frac{{\rho }^2}{R}\frac{d^{2}R}{d{\rho }^2}+-\frac{2m}{{\hslash }^2}\left(E-V(\rho )\right){\rho }^2\right)+\frac{1}{F}\frac{d^{2}F}{d{\phi }^2}=0\end{array}}$

El primer término, solamente depende de ρ, el segundo de φ, la ecuación diferencial se transforma en el sistema de dos ecuaciones diferenciales

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{\rho }{R}\frac{dR}{d\rho }+\frac{{\rho }^2}{R}\frac{d^{2}R}{d{\rho }^2}+\frac{2m}{{\hslash }^2}\left(E-V(\rho )\right){\rho }^2=n_{\phi }^2\\ \frac{1}{F}\frac{d^{2}F}{d{\phi }^2}=-n_{\phi }^2\end{array}\\ \{\begin{array}{l}{\rho }^2\frac{d^{2}R}{d{\rho }^2}+\rho \frac{dR}{d\rho }+\left(\frac{2m}{{\hslash }^2}\left(E-V(\rho )\right){\rho }^2-n_{\phi }^2\right)R=0\\ \frac{d^{2}F}{d{\phi }^2}+n_{\phi }^{2}F=0\end{array}\end{array}}$

La ecuación angular

${\displaystyle \frac{d^{2}F}{d{\phi }^2}+n_{\phi }^{2}F=0}$

La misma solución que en el primer apartado

La ecuación radial

Resolvemos la ecuaciones diferenciales

• En la región ρ>a

${\displaystyle {\rho }^2\frac{d^{2}R}{d{\rho }^2}+\rho \frac{dR}{d\rho }-\left(n_{\phi }^2+k^2{\rho }^2\right)R=\mathrm{0,}{k}^2=-\frac{2mE}{{\hslash }^2}}$

Los estados ligados solamente existen para E<0. Escribiendo kρ=x

${\displaystyle x^2\frac{d^{2}R}{d{x}^2}+x\frac{dR}{dx}-\left(n_{\phi }^2+x^2\right)R=0}$

La solución de esta ecuación diferencial es de la forma

${\displaystyle R(x)=C{I}_{n_{\phi }}(x)+D{K}_{n_{\phi }}(x),x>0}$

Como I_nφ(x)→∞ cuando x→∞. La solución es

${\displaystyle R(\alpha \rho )=D{K}_{n_{\phi }}(\alpha \rho )}$

• En la región ρ<a

${\displaystyle {\rho }^2\frac{d^{2}R}{d{\rho }^2}+\rho \frac{dR}{d\rho }+\left(q^2{\rho }^2-n_{\phi }^2\right)R=\mathrm{0,}{q}^2=\frac{2m}{{\hslash }^2}\left(E+V_0\right)}$

Sustituyendo y=qρ

${\displaystyle y^2\frac{d^{2}R}{d{y}^2}+y\frac{dR}{dy}+\left(y^2-n_{\phi }^2\right)R=0}$

La solución de esta ecuación diferencial es de la forma

${\displaystyle R(y)=A{J}_{n_{\phi }}(y)+B{Y}_{n_{\phi }}(y)}$

Como Y_nφ(x)→∞ cuando x→∞. La solución es

${\displaystyle R(q\rho )=A{J}_{n_{\phi }}(q\rho )}$

Niveles de energía

La continuidad en ρ=a exige que

${\displaystyle \begin{array}{l}\{\begin{array}{l}R(ka)=R(qa)\\ {\frac{dR(k\rho )}{d\rho }|}_{\rho =a}={\frac{dR(q\rho )}{d\rho }|}_{\rho =a}\end{array}\\ \{\begin{array}{l}D{K}_{n_{\phi }}(ka)=A{J}_{n_{\phi }}(qa)\\ {D\frac{d{K}_{n_{\phi }}(k\rho )}{d\rho }|}_{\rho =a}=A{\frac{d{J}_{n_{\phi }}(q\rho )}{d\rho }|}_{\rho =a}\end{array}\end{array}}$

Dividiendo

${\displaystyle \frac{{\frac{d{K}_{n_{\phi }}(k\rho )}{d\rho }|}_{\rho =a}}{K_{n_{\phi }}(ka)}=\frac{{\frac{dJ{n}_{\phi }(q\rho )}{d\rho }|}_{\rho =a}}{J_{n_{\phi }}(qa)}}$

Teniendo en cuenta

${\displaystyle \begin{array}{l}u=kx\\ \frac{d}{dx}f(kx)=k\frac{d}{du}f(u)\end{array}}$

y las derivadas de las funciones de Bessel

${\displaystyle \begin{array}{l}\frac{d{K}_n(x)}{dx}=-K_{n-1}(x)-\frac{n}{x}{K}_n(x)\\ \frac{d{J}_n(x)}{dx}=\frac{n}{x}{J}_n(x)-J_{n+1}(x)\end{array}}$

La ecuación tanscendente que calcula los niveles de energía es

${\displaystyle \begin{array}{l}-\left(ka\right)\frac{K_{n_{\phi }-1}(ka)+\frac{n_{\phi }}{ka}{K}_{n_{\phi }}(ka)}{K_{n_{\phi }}(ka)}=\left(qa\right)\frac{\frac{n_{\phi }}{qa}{J}_{n_{\phi }}(qa)-J_{n_{\phi }+1}(qa)}{J_{n_{\phi }}(qa)}\\ q^2+k^2=\frac{2m}{{\hslash }^2}{V}_0\end{array}}$

Expresamos la ecuación transcendente de forma adecuada para aplicar el procedimiento numérico que calcula las raíces de ka mediante el rpocedimiento fzero de MATLAB

${\displaystyle \begin{array}{l}2n_{\phi }+\left(ka\right)\frac{K_{n_{\phi }-1}(ka)}{K_{n_{\phi }}(ka)}-\left(qa\right)\frac{J_{n_{\phi }+1}(qa)}{J_{n_{\phi }}(qa)}=0\\ 2n_{\phi }{K}_{n_{\phi }}(ka)J_{n_{\phi }}(qa)+\left(ka\right)K_{n_{\phi }-1}(ka)J_{n_{\phi }}(qa)-\left(qa\right)J_{n_{\phi }+1}(qa)K_{n_{\phi }}(ka)=0\\ {\left(qa\right)}^2=r_0^2-{\left(ka\right)}^2,k^2=-\frac{2mE}{{\hslash }^2},r_0^2=\frac{2m}{{\hslash }^2}{V}_0\end{array}}$

Denominamos ${\xi }_{n_{\phi },n_{\rho }}$ a las raíces de la ecuación transcendente, por lo que el parámetro k vale

${\displaystyle k=\frac{{\xi }_{n_{\phi },n_{\rho }}}{a},n_{\rho }=\mathrm{1,2,3...}}$

n_ρ es el índice de la raíz

La energía de los niveles es

${\displaystyle E=-\frac{{\hslash }^2{k}^2}{2m}}$

Función de onda

Es el producto de las dos soluciones

${\displaystyle \psi (\rho ,\phi )=R(\rho )·F(\phi )}$

La función de onda ha de cumplir

${\displaystyle \begin{array}{l}{\displaystyle \int {\displaystyle \int \psi (\rho ,\phi )}}·{\psi }^{*}(\rho ,\phi )·\left(\rho ·d\rho ·d\phi \right)=\\ \left({\displaystyle \underset{0}{\overset{a}{\int }}\rho ·R(\rho )R^{*}(\rho )d\rho }\right)\left({\displaystyle \underset{0}{\overset{2\pi }{\int }}F(\phi )F^{*}(\phi )·d\phi }\right)=1\end{array}}$

Repitiendo los mismos cálculos que en el apartado anterior

• La parte radial de la función de onda es

${\displaystyle \begin{array}{l}R(\rho )\{\begin{array}{l}A{J}_{n_{\phi }}(q\rho ),\rho \le a\\ D{K}_{n_{\phi }}(k\rho ),\rho >a\end{array}\\ A{J}_{n_{\phi }}(qa)=D{K}_{n_{\phi }}(ka)\end{array}}$

La primera integral es

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\infty }{\int }}\rho ·R(\rho )R^{*}(\rho )d\rho }=A^2\left\{{\displaystyle \underset{0}{\overset{a}{\int }}\rho ·J_{n_{\phi }}^2\left(q\rho \right)d\rho }+\frac{J_{n_{\phi }}^2(qa)}{K_{n_{\phi }}^2(ka)}{\displaystyle \underset{a}{\overset{\infty }{\int }}\rho ·K_{n_{\phi }}^2\left(k\rho \right)d\rho }\right\}=1\\ {\displaystyle \underset{0}{\overset{a}{\int }}\rho ·J_{n_{\phi }}^2\left(q\rho \right)d\rho }=a^2{\displaystyle \underset{0}{\overset{1}{\int }}x·J_{n_{\phi }}^2\left(qax\right)dx}=\frac{1}{2}{a}^2{J}_{n_{\phi }+1}^2\left(qa\right),x=\frac{\rho }{a}\\ {\displaystyle \underset{a}{\overset{\infty }{\int }}\rho ·K_{n_{\phi }}^2\left(k\rho \right)d\rho }=a^2{\displaystyle \underset{1}{\overset{\infty }{\int }}x·K_{n_{\phi }}^2\left(kax\right)dx}\\ A^2{a}^2\left\{\frac{1}{2}{J}_{n_{\phi }+1}^2\left(qa\right)+\frac{J_{n_{\phi }}^2(qa)}{K_{n_{\phi }}^2(ka)}{\displaystyle \underset{1}{\overset{\infty }{\int }}x·K_{n_{\phi }}^2\left(kax\right)dx}\right\}=1\end{array}}$

Se despeja el coeficiente A y luego, el coeficiente D

Representamos la parte radial de la función de onda R(ρ)

function pozo_polar_4
    n_phi=0;
    r0=8;
    f=@(x) 2*n_phi*besselk(n_phi,x).*besselj(n_phi,sqrt(r0^2-x.^2))+x.*
besselk(n_phi-1,x).*besselj(n_phi,sqrt(r0^2-x.^2))-sqrt(r0^2-x.^2).*
besselj(n_phi+1,sqrt(r0^2-x.^2)).*besselk(n_phi,x);
    xx=linspace(0,r0,20);
    ceros=raices(f,xx);
    rr=fliplr(ceros); %invierte el orden
    disp([r0,-rr.^2]) %energía
    
    hold on
    for n=1:length(rr)
        suma=besselj(n_phi+1, sqrt(r0^2-rr(n)^2))^2/2+besselj(n_phi, 
sqrt(r0^2-rr(n)^2))^2*integral(@(x) x.*besselk(n_phi, rr(n)*x),1, 100)
/besselk(n_phi, rr(n))^2;
        A=1/sqrt(suma);
        D=A*besselj(n_phi, sqrt(r0^2-rr(n)^2))/besselk(n_phi, rr(n));
        fplot(@ (rho) A*besselj(n_phi, sqrt(r0^2-rr(n)^2)*rho), [0,1])
        fplot(@ (rho) D*besselk(n_phi, rr(n)*rho), [1,3])
    end
    xlabel('\rho')
    ylabel('R(\rho)')
    grid on
    title('Función radial') 
  
    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

• Para n_φ=0



• Para n_φ=1



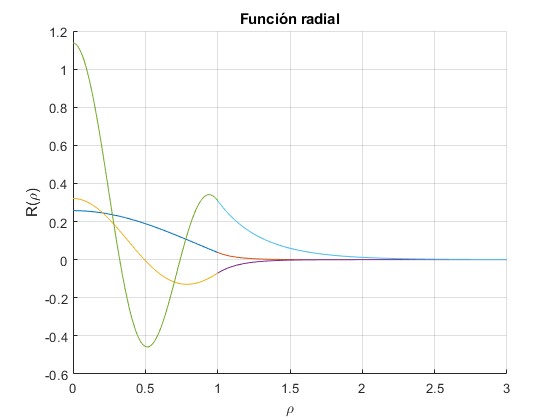
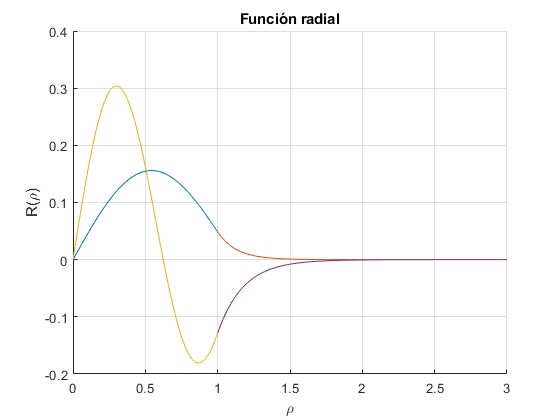
• La parte angular de la función de onda

${\displaystyle F(\phi )=\frac{1}{\sqrt{2\pi }}\exp (i{n}_{\phi }\phi )}$

La segunda integral

${\displaystyle {\displaystyle \underset{0}{\overset{2\pi }{\int }}F(\phi )F^{*}(\phi )·d\phi }=1}$

La parte real de la función de onda es

${\displaystyle \psi (\rho ,\phi )=\frac{1}{\sqrt{2\pi }}\cos \left(n_{\phi }\phi \right)\{\begin{array}{l}A{J}_{n_{\phi }}\left(\sqrt{r_0^2-{\xi }_{n_{\phi },n_{\rho }}^2}\frac{\rho }{a}\right),\rho \le a\\ D{K}_{n_{\phi }}\left({\xi }_{n_{\phi },n_{\rho }}\frac{\rho }{a}\right),\rho >a\end{array},\{\begin{array}{l}{n}_{\phi }=\mathrm{0,1,2,3...}\\ n_{\rho }=\mathrm{1,2,3...}\end{array}}$

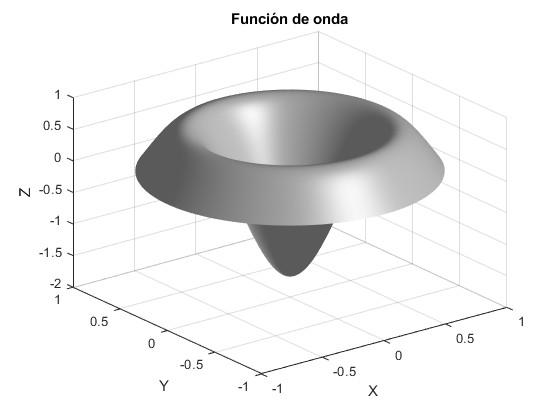
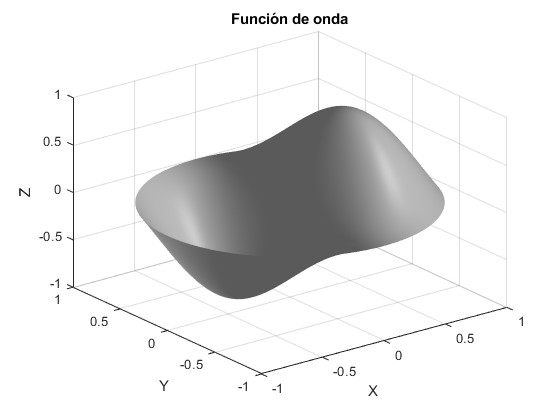
Dado r₀ o bien, la profundidad V₀ del pozo de potencial, representamos la función de onda para algunos valores de n_φ y n_ρ

function pozo_polar_3
    n_phi=0;
    r0=8;
    f=@(x) 2*n_phi*besselk(n_phi,x).*besselj(n_phi,sqrt(r0^2-x.^2))+x.*
besselk(n_phi-1,x).*besselj(n_phi,sqrt(r0^2-x.^2))-sqrt(r0^2-x.^2).*
besselj(n_phi+1,sqrt(r0^2-x.^2)).*besselk(n_phi,x);
    xx=linspace(0,r0,20);
    ceros=raices(f,xx);
    rr=fliplr(ceros); %invierte el orden
    disp([r0,-rr.^2]) %energía
    
    n=1; %raíz número
    suma=besselj(n_phi+1, sqrt(r0^2-rr(n)^2))^2/2+besselj(n_phi,
sqrt(r0^2-rr(n)^2))^2*integral(@(x) x.*besselk(n_phi, rr(n)*x),1, 100)
/besselk(n_phi, rr(n))^2;
    A=1/sqrt(suma);
    D=A*besselj(n_phi, sqrt(r0^2-rr(n)^2))/besselk(n_phi, rr(n));
    hold on
    rho=linspace(0,1,20);
    phi=linspace(0,2*pi, 100);
    [Rho,Phi]=meshgrid(rho,phi);
    X=Rho.*cos(Phi);
    Y=Rho.*sin(Phi);
    Z=A*cos(n_phi*Phi).*besselj(n_phi, sqrt(r0^2-rr(n)^2)*rho)/sqrt(2*pi);
    surfl(X,Y,Z)
    rho=linspace(1,3,50);
    phi=linspace(0,2*pi, 100);
    [Rho,Phi]=meshgrid(rho,phi);
    X=Rho.*cos(Phi);
    Y=Rho.*sin(Phi);
    Z=D*cos(n_phi*Phi).*besselk(n_phi, rr(n)*rho)/sqrt(2*pi);
    surfl(X,Y,Z)
    shading interp
    colormap(gray);
    xlabel('X')
    ylabel('Y')
    zlabel('Z')
    grid on
    title('Función de onda') 
    view(-15,15)

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

• n_φ=0, n_ρ=1. La primera raíz de la ecuación transcendente es -59.4436.



• n_φ=0, n_ρ=2. La segunda raíz de la ecuación transcendente es -40.3240.



• n_φ=1, n_ρ=1. La primera raíz de la ecuación transcendente es -52.4787.



• n_φ=1, n_ρ=2. La segunda raíz de la ecuación transcendente es -26.2692.

Referencias

Arkadiy S. Baltenkov, Alfred Z. Msezane. Electronic quantum confinement in cylindrical potential well. Eur. Phys. J. D (2016) 70: 81

Young-Sea Huang, Tzuu-Kang Chyi, Kung-Te Wu. The right way to solve the infinite circular well in quantum mechanics. Preprint, August 2018

Nagalakshmi A Rao, Shivalingaswamy T, Kagali B.A. Eigenstates of a Non-Relativistic Particle in a Two-Dimensional Square Well Potential. Physics Education. Jul - Sep 2014.