El oscilador armónico en dos dimensiones
Coordenadas rectangulares
La ecuación de Schrödinger independiente del tiempo para una partícula de masa me en el potencial armónico V(x,y)
Tomamos una escala de energías y distancias
La ecuación de Schrödinger se transforma en otra más simple
Probamos la solución Ψ(ξ,η)=X(ξ)Y(η), separación de variables
El primer término, es una función solamente de ξ, el segundo, de η. Esta ecuación diferencial se convierte en el sistema de dos ecuaciones diferenciales
Haciendo un cambio de variable, la primera ecuación diferencial se transforma en la de Hermite
Del mismo modo, la segunda
Cuya solución son los polinomios de Hermite
Los niveles de energía ε son
Cuando nx=1 y ny=0, la energía es ε1,0=2. Cuando nx=0 y ny=1, la energía es la misma. Dos estados con la misma energía
Las funciones de onda
Donde C es una constante a determinar
Se ha tenido en cuenta las relaciones de ortogonalidad de los polinomios de Hermite. El resultado final es
Comprobaremos en los ejemplos que
Ejemplos
Ψ0,0(ξ,η)
[x,y] = meshgrid(-5:0.2:5);
z = exp(-(x.^2+y.^2)/2)/sqrt(pi);
surf(x,y,z)
xlabel('x');
ylabel('y');
zlabel('z')
title('\Psi_{0,0}')
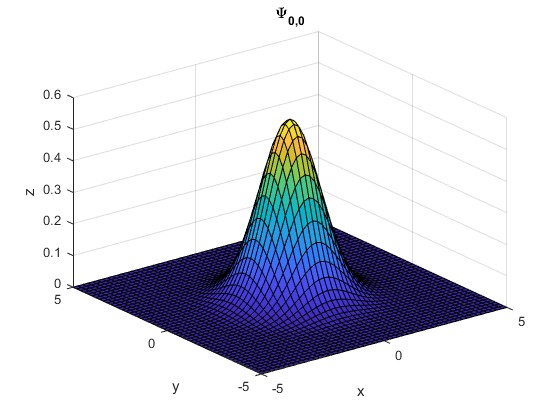
Comprobación.
>> syms x y; >> int(exp(-x^2),x,-inf,inf)*int(exp(-y^2),y,-inf,inf)/pi ans =1
Ψ1,0(ξ,η)
[x,y] = meshgrid(-5:0.2:5);
z = x.*exp(-(x.^2+y.^2)/2)*sqrt(2/pi);
surf(x,y,z)
xlabel('x');
ylabel('y');
zlabel('z')
title('\Psi_{1,0}')
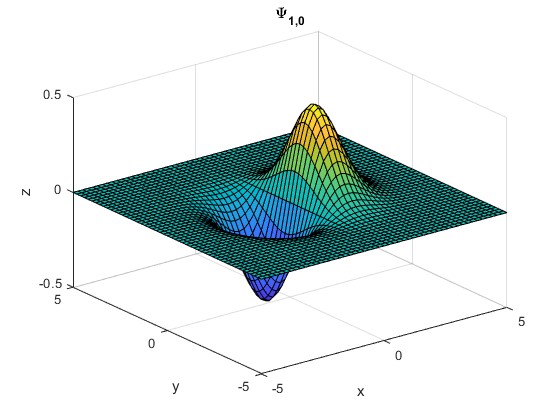
Comprobación.
>> syms x y; >> int(x^2*exp(-x^2),x,-inf,inf)*int(exp(-y^2),y,-inf,inf)*2/pi ans =1
Ψ2,0(ξ,η)
[x,y] = meshgrid(-5:0.2:5);
z = (4*x.^2-2).*exp(-(x.^2+y.^2)/2)/sqrt(8*pi);
surf(x,y,z)
xlabel('x');
ylabel('y');
zlabel('z')
title('\Psi_{2,0}')
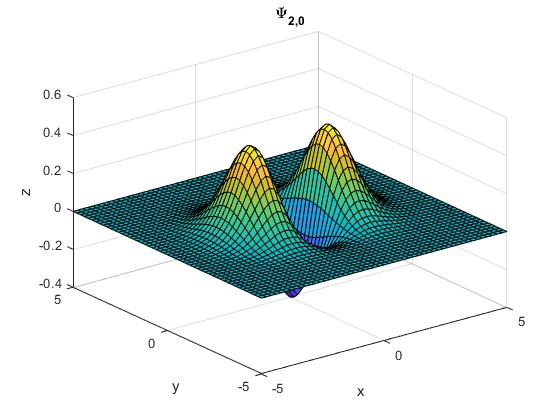
Comprobación.
>> syms x y; >> int((4*x^2-2)^2*exp(-x^2),x,-inf,inf)*int(exp(-y^2),y,-inf,inf)/(8*pi) ans =1
Ψ2,1(ξ,η)
[x,y] = meshgrid(-5:0.2:5);
z = y.*(4*x.^2-2).*exp(-(x.^2+y.^2)/2)/sqrt(4*pi);
surf(x,y,z)
xlabel('x');
ylabel('y');
zlabel('z')
title('\Psi_{2,1}')
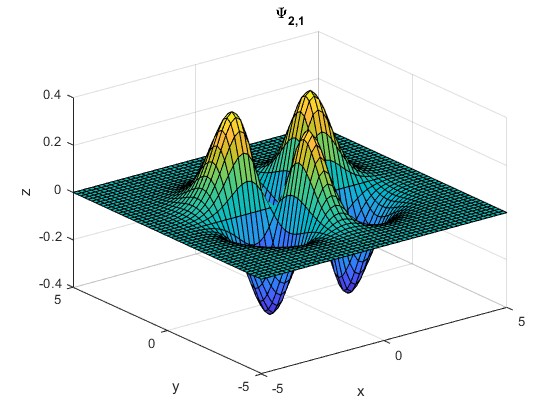
Comprobación.
>> syms x y; >> int((4*x^2-2)^2*exp(-x^2),x,-inf,inf)*int(y^2*exp(-y^2),y,-inf,inf)/(4*pi) ans =1
Coordenadas polares
Resolveremos la ecuación de Schrödinger independiente del tiempo en coordenadas polares, para el potencial V(r). Donde me es la masa de la partícula
Intentamos la separación de variables
El primer término, solamente depende de r, el segundo de φ, la ecuación diferencial se transforma en el sistema de dos ecuaciones diferenciales
La ecuación angular
Tiene una solución conocida, que expresamos de forma equivalente
La solución es periódica, Φ(φ+2π)=Φ(φ). m tiene que ser un entero.
La ecuación radial
Haciendo el cambio de variable, la ecuación radial se transforma en
Definimos
Calculamos la derivada primera y segunda de R respecto de x
Obtenemos una ecuación diferencial en G
Hacemos el cambio de variable ξ=x2
Es una ecuación del tipo
que se denomina hipergeométrica confluente, cuya solución es
n es un número entero positivo (incluido cero) que se denomina número cuántico principal. Los niveles de energía se han obtenido en el primer apartado, ε=nx+ny+1=k+1, k=0,1,2,3...
Dado el entero k, para que n sea entero, los posibles valores de |m| se recogen en la tabla
| n | |m| |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 0, 2 |
| 3 | 1, 3 |
| 4 | 0,2,4 |
Las funciones de onda radiales Rnm(r) son
Esta función hipergeométrica está relacionada con los polinomios asociados de Laguerre del siguiente modo
Funciones radiales Rnm(r)
Comprobaremos utilizando la función
La integral
también
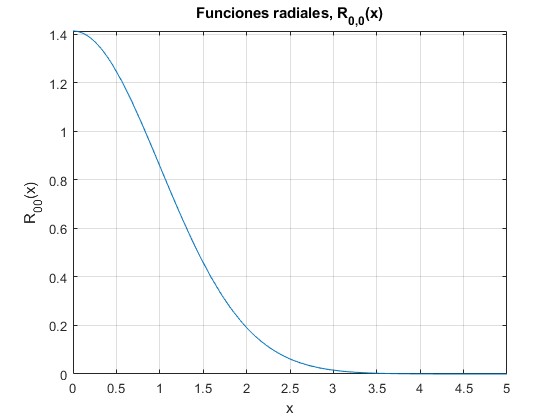
R00(r)
Representamos R00(x) en función de x
f=@(x) sqrt(2)*exp(-x.^2/2);
fplot(f,[0,5])
grid on
xlabel('x')
ylabel('R_{00}(x)')
title('Funciones radiales, R_{0,0}(x)')
>> syms x; >> int(x*exp(-x^2),x,0,inf)*2 ans =1
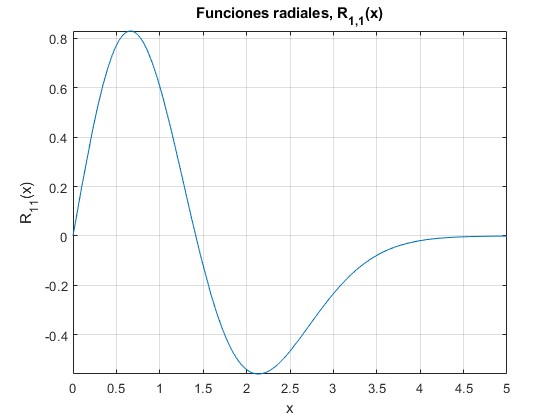
R11(x)
f=@(x) (x.*exp(-x.^2/2)).*(2-x.^2);
fplot(f,[0,5])
grid on
xlabel('x')
ylabel('R_{11}(x)')
title('Funciones radiales, R_{1,1}(x)')
>> syms x; >> int(x^3*(2-x^2)^2*exp(-x^2),x,0,inf) ans =1
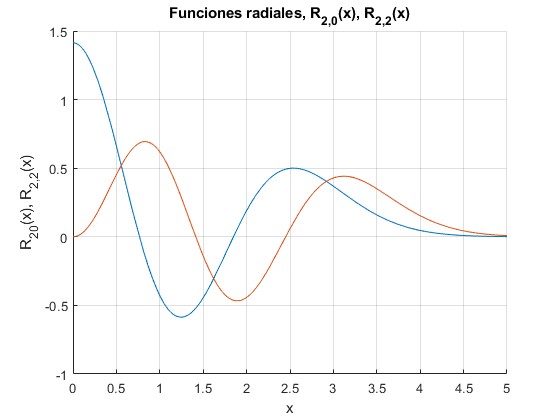
R20(x)
R22(x)
hold on
f=@(x) sqrt(2)*exp(-x.^2/2).*(x.^4/2-2*x.^2+1);
fplot(f,[0,5])
g=@(x) (x.^2.*exp(-x.^2/2)).*(x.^4/2-4*x.^2+6)/sqrt(6);
fplot(g,[0,5])
hold off
grid on
xlabel('x')
ylabel('R_{20}(x), R_{2,2}(x)')
title('Funciones radiales, R_{2,0}(x), R_{2,2}(x)')
>> syms x; >> 2*int(x*(1-x^2)^2*exp(-x^2),x,0,inf) ans =1 >> int(x^5*(x^4/2-4*x^2+6)^2*exp(-x^2),x,0,inf)/6 ans =1
R31(x)
R33(x)
hold on
f1=@(x) sqrt(2)*(exp(-x.^2/2).*x).*(-x.^6+12*x.^4-36*x.^2+24)/12;
fplot(f1,[0,5])
f2=@(x) (exp(-x.^2/2).*x.^3).*(-x.^6+18*x.^4-90*x.^2+120)/(6*sqrt(60));
fplot(f2,[0,5])
hold off
grid on
xlabel('x')
ylabel('R_{3,1}(x), R_{3,3}(x)')
title('Funciones radiales, R_{3,1}(x), R_{3,3}(x)')
>> syms x; >> int(x^3*(-x^6+12*x^4-36*x^2+24)^2*exp(-x^2),x,0,inf)/72 ans =1 >> int(x^7*(-x^6+18*x^4-90*x^2+120)^2*exp(-x^2),x,0,inf)/(36*60) ans =1
Alternativamente, utilizamos la función
hold on
f1=@(x) sqrt(2)*(exp(-x.^2/2).*x).*laguerreL(3,1,x.^2)/2;
fplot(f1,[0,5])
f2=@(x) (exp(-x.^2/2).*x.^3).*laguerreL(3,3,x.^2)/sqrt(60);
fplot(f2,[0,5])
hold off
grid on
xlabel('x')
ylabel('R_{3,1}(x), R_{3,3}(x)')
title('Funciones radiales, R_{3,1}(x), R_{3,3}(x)')
>> int((exp(-x.^2).*x.^3).*laguerreL(3,1,x.^2).^2/2,x,0,inf) ans =1 >> int((exp(-x.^2).*x.^7).*laguerreL(3,3,x.^2).^2/60,x,0,inf) ans =1
Referencias
Xijin Fu. Study on two - dimensional linear harmonic oscillator characteristics based on MATLAB software. IOP Conf. Series: Earth and Environmental Science 295(2019) 032042. IOP Publishing

