Coordenadas rectangulares

La ecuación de Schrödinger independiente del tiempo para una partícula de masa m_e en el potencial armónico V(x,y,z)

${\displaystyle -\frac{{\hslash }^2}{2m_e}\left(\frac{{\partial }^2\psi (x,y,z)}{\partial x^2}+\frac{{\partial }^2\psi (x,y,z)}{\partial y^2}+\frac{{\partial }^2\psi (x,y,z)}{\partial z^2}\right)+\frac{1}{2}{m}_e{\omega }^2\left(x^2+y^2+z^2\right)\psi (x,y,z)=E\psi (x,y,z)}$

Tomamos una escala de energías y distancias

${\displaystyle x=\xi \sqrt{\frac{\hslash }{m\omega }},y=\eta \sqrt{\frac{\hslash }{m\omega }},z=\zeta \sqrt{\frac{\hslash }{m\omega }},E=\hslash \omega \epsilon }$

La ecuación de Schrödinger se transforma en otra más simple

${\displaystyle \begin{array}{l}-\frac{{\partial }^2\psi (\xi ,\eta ,\zeta )}{\partial {\xi }^2}-\frac{{\partial }^2\psi (\xi ,\eta ,\zeta )}{\partial {\eta }^2}-\frac{{\partial }^2\psi (\xi ,\eta ,\zeta )}{\partial {\zeta }^2}+\left({\xi }^2+{\eta }^2+{\zeta }^2\right)\psi (\xi ,\eta ,\zeta )=2\epsilon \psi (\xi ,\eta ,\zeta )\\ \frac{{\partial }^2\psi (\xi ,\eta ,\zeta )}{\partial {\xi }^2}+\frac{{\partial }^2\psi (\xi ,\eta ,\zeta )}{\partial {\eta }^2}+\frac{{\partial }^2\psi (\xi ,\eta ,\zeta )}{\partial {\zeta }^2}+\left\{2\epsilon -\left({\xi }^2+{\eta }^2+{\zeta }^2\right)\right\}\psi (\xi ,\eta ,\zeta )=0\end{array}}$

Probamos la solución Ψ(ξ,η, ζ)=X(ξ)Y(η)Z(ζ), separación de variables

${\displaystyle \begin{array}{l}Y(\eta )Z(\zeta )\frac{d^{2}X(\xi )}{d{\xi }^2}+X(\xi )Z(\zeta )\frac{d^{2}Y(\eta )}{d{\eta }^2}+X(\xi )Y(\eta )\frac{d^{2}Z(\zeta )}{d{\zeta }^2}+\left\{2\epsilon -\left({\xi }^2+{\eta }^2+{\zeta }^2\right)\right\}X(\xi )Y(\eta )Z(\zeta )=0\\ \frac{1}{X(\xi )}\frac{d^{2}X(\xi )}{d{\xi }^2}+\left\{2{\epsilon }_x-{\xi }^2\right\}+\frac{1}{Y(\eta )}\frac{d^{2}Y(\eta )}{d{\eta }^2}+\left\{2{\epsilon }_y-{\eta }^2\right\}+\frac{1}{Z(\zeta )}\frac{d^{2}Z(\zeta )}{d{\zeta }^2}+\left\{2{\epsilon }_z-{\zeta }^2\right\}=\mathrm{0,}{\epsilon }_x+{\epsilon }_y+{\epsilon }_z=\epsilon \end{array}}$

El primer término, es una función solamente de ξ, el segundo, de η y el tercero de ζ. Esta ecuación diferencial se convierte en el sistema de tres ecuaciones diferenciales

${\displaystyle \{\begin{array}{l}\frac{d^{2}X(\xi )}{d{\xi }^2}+\left\{2{\epsilon }_x-{\xi }^2\right\}X(\xi )=0\\ \frac{d^{2}Y(\eta )}{d{\eta }^2}+\left\{2{\epsilon }_y-{\eta }^2\right\}Y(\eta )=0\\ \frac{d^{2}Z(\zeta )}{d{\zeta }^2}+\left\{2{\epsilon }_z-{\zeta }^2\right\}Z(\zeta )=0\end{array}}$

Haciendo un cambio de variable, la primera ecuación diferencial se transforma en la de Hermite

${\displaystyle \begin{array}{l}X(\xi )=x(\xi )\exp \left(-\frac{{\xi }^2}{2}\right)\hfill \\ \frac{dX}{d\xi }=\exp \left(-\frac{{\xi }^2}{2}\right)\frac{dx}{d\xi }-\xi \exp \exp \left(-\frac{{\xi }^2}{2}\right)x\hfill \\ \frac{d^{2}X}{d{\xi }^2}=\exp \left(-\frac{{\xi }^2}{2}\right)\frac{d^{2}x}{d{\xi }^2}-\xi \exp \left(-\frac{{\xi }^2}{2}\right)\frac{dx}{d\xi }-\exp \left(-\frac{{\xi }^2}{2}\right)x+{\xi }^2\exp \left(-\frac{{\xi }^2}{2}\right)x-\xi \exp \left(-\frac{{\xi }^2}{2}\right)\frac{dx}{d\xi }\hfill \\ \frac{d^{2}x}{d{\xi }^2}-2\xi \frac{dx}{d\xi }+(2{\epsilon }_x-1)x=0\hfill \end{array}}$

Del mismo modo, la segunda y la tercera

${\displaystyle \begin{array}{l}\frac{d^{2}y}{d{\eta }^2}-2\eta \frac{dy}{d\eta }+(2{\epsilon }_y-1)y=0\\ \frac{d^{2}z}{d{\zeta }^2}-2\zeta \frac{dz}{d\zeta }+(2{\epsilon }_z-1)z=0\end{array}}$

Cuyas soluciones son los polinomios de Hermite

Los niveles de energía ε son

${\displaystyle \begin{array}{l}\{\begin{array}{l}2{\epsilon }_x-1=2n_x,{\epsilon }_x=n_x+\frac{1}{2},n_x=\mathrm{0,1,2,3...}\\ 2{\epsilon }_y-1=2n_y,{\epsilon }_y=n_y+\frac{1}{2},n_y=\mathrm{0,1,2,3...}\\ 2{\epsilon }_z-1=2n_z,{\epsilon }_z=n_z+\frac{1}{2},n_z=\mathrm{0,1,2,3...}\end{array}\\ \epsilon ={\epsilon }_x+{\epsilon }_y+{\epsilon }_z=n_x+n_y+n_z+\frac{3}{2}\end{array}}$

Como apreciamos en la tabla hay

• un estado con k=n_x+n_y+n_z=0
• tres estados con k=1
• seis estados con k=2

En general, el número de estados con la misma energía k viene dado por la fórmula

${\displaystyle \frac{(k+2)!}{k!·2!}}$

Las funciones de onda

Las soluciones de las tres ecuaciones diferenciales son los polinomios de Hermite

${\displaystyle \begin{array}{l}x(\xi )=C_x·H_{n_x}(\xi ),y(\eta )=C_y·H_{n_y}(\eta ),z(\zeta )=C_z·H_{n_z}(\zeta )\\ {\psi }_{n_x,n_y,n_z}\left(\xi ,\eta ,\zeta \right)=C·H_{n_x}(\xi )H_{n_y}(\eta )H_{n_z}(\zeta )\exp \left(-\frac{{\xi }^2+{\eta }^2+{\zeta }^2}{2}\right)\end{array}}$

Donde C es una constante a determinar, de modo que

${\displaystyle \begin{array}{l}\begin{array}{l}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\left|{\psi }_{n_x,n_y,n_z}\left(\xi ,\eta ,\zeta \right)\right|}^{2}d\xi ·d\eta ·d\zeta }=1}}\\ C^2{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{H}_{n_x}^2(\xi )\exp \left(-{\xi }^2\right)d\xi }·{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{H}_{n_y}^2(\eta )\exp \left(-{\eta }^2\right)d\eta ·{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{H}_{n_z}^2(\zeta )\exp \left(-{\zeta }^2\right)d\zeta =1}}\end{array}\hfill \\ C^2\left(\sqrt{\pi }{2}^{n_x}{n}_x!\right)\left(\sqrt{\pi }{2}^{n_y}{n}_y!\right)\left(\sqrt{\pi }{2}^{n_z}{n}_z!\right)=1\hfill \end{array}}$

Se ha tenido en cuenta las relaciones de ortogonalidad de los polinomios de Hermite. El resultado final es

${\displaystyle {\psi }_{n_x,n_y,n_z}\left(\xi ,\eta ,\zeta \right)=\frac{H_{n_x}(\xi )H_{n_y}(\eta )H_{n_z}(\zeta )}{\sqrt{\pi ·\sqrt{\pi }{2}^{n_x+n_y+n_z}{n}_x!·n_y!·n_z!}}\exp \left(-\frac{{\xi }^2+{\eta }^2+{\zeta }^2}{2}\right)}$

Algunos ejemplos

${\displaystyle \begin{array}{l}{\psi }_{\mathrm{0,0,0}}\left(\xi ,\eta ,\zeta \right)=\frac{1}{\sqrt{\pi \sqrt{\pi }·2^0·0!·0!·0!}}{H}_0(\xi )H_0(\eta )H_0(\zeta )\exp \left(-\frac{{\xi }^2+{\eta }^2+{\zeta }^2}{2}\right)=\frac{1}{\sqrt{\pi \sqrt{\pi }}}\exp \left(-\frac{{\xi }^2+{\eta }^2+{\zeta }^2}{2}\right)\\ {\psi }_{\mathrm{1,0,0}}\left(\xi ,\eta ,\zeta \right)=\frac{1}{\sqrt{\pi \sqrt{\pi }·2^1·1!·0!·0!}}{H}_1(\xi )H_0(\eta )H_0(\zeta )\exp \left(-\frac{{\xi }^2+{\eta }^2+{\zeta }^2}{2}\right)=\frac{1}{\sqrt{2\pi \sqrt{\pi }}}2\xi \exp \left(-\frac{{\xi }^2+{\eta }^2+{\zeta }^2}{2}\right)\\ {\psi }_{\mathrm{2,0,0}}\left(\xi ,\eta ,\zeta \right)=\frac{1}{\sqrt{\pi \sqrt{\pi }·2^2·2!·0!·0!}}{H}_2(\xi )H_0(\eta )H_0(\zeta )\exp \left(-\frac{{\xi }^2+{\eta }^2+{\zeta }^2}{2}\right)=\frac{1}{2\sqrt{2\pi \sqrt{\pi }}}\left(4{\xi }^2-2\right)\exp \left(-\frac{{\xi }^2+{\eta }^2+{\zeta }^2}{2}\right)\\ {\psi }_{\mathrm{2,1,0}}\left(\xi ,\eta ,\zeta \right)=\frac{1}{\sqrt{\pi \sqrt{\pi }·2^3·2!·1!·0!}}{H}_2(\xi )H_1(\eta )H_0(\zeta )\exp \left(-\frac{{\xi }^2+{\eta }^2+{\zeta }^2}{2}\right)=\frac{1}{2\sqrt{\pi \sqrt{\pi }}}\eta \left(4{\xi }^2-2\right)\exp \left(-\frac{{\xi }^2+{\eta }^2+{\zeta }^2}{2}\right)\end{array}}$

Coordenadas polares

La ecuación diferencial de la parte radial para el potencial V(r)

${\displaystyle \frac{1}{r^2}\frac{d}{dr}\left(r^2\frac{dR}{dr}\right)+\left\{\frac{2m_e}{{\hslash }^2}\left(E-V(r)\right)-\frac{l(l+1)}{r^2}\right\}R=0}$

Donde m_e es la masa de la partícula, V(r)=m_eω²r²/2, R(r) es la componente radial de la función de onda

${\displaystyle \frac{d}{dr}\left(r^2\frac{dR}{dr}\right)+\left\{\frac{2m_e}{{\hslash }^2}\left(E-\frac{1}{2}{m}_e{\omega }^2{r}^2\right)r^2-l(l+1)\right\}R=0}$

Haciendo el cambio de variable, la ecuación diferencial se transforma en

${\displaystyle \begin{array}{l}E=\hslash \omega \epsilon ,r=\sqrt{\frac{\hslash }{m_e\omega }}x\\ \frac{d}{dx}\left(x^2\frac{dR}{dx}\right)+\left\{\frac{2m_e}{{\hslash }^2}\left(\hslash \omega \epsilon -\frac{1}{2}{m}_e{\omega }^2\frac{\hslash }{m_e\omega }{x}^2\right)\frac{\hslash }{m_e\omega }{x}^2-l(l+1)\right\}R=0\\ \frac{d^{2}R}{d{x}^2}+\frac{2}{x}\frac{dR}{dx}+\left\{2\epsilon -x^2-\frac{l(l+1)}{x^2}\right\}R=0\end{array}}$

Definimos, u(x)=xR(x), calculamos la derivada primera y segunda de R respecto de x y las introducimos en la ecuación diferencial

${\displaystyle \begin{array}{l}\frac{dR}{dx}=-\frac{1}{x^2}u+\frac{1}{x}\frac{du}{dx}\\ \frac{d^{2}R}{d{x}^2}=\frac{2}{x^3}u-\frac{1}{x^2}\frac{du}{dx}-\frac{1}{x^2}\frac{du}{dx}+\frac{1}{x}\frac{d^{2}u}{d{x}^2}=\frac{2}{x^3}u-\frac{2}{x^2}\frac{du}{dx}+\frac{1}{x}\frac{d^{2}u}{d{x}^2}\\ \frac{2}{x^3}u-\frac{2}{x^2}\frac{du}{dx}+\frac{1}{x}\frac{d^{2}u}{d{x}^2}+\frac{2}{x}\left(-\frac{1}{x^2}u+\frac{1}{x}\frac{du}{dx}\right)+\left\{2\epsilon -x^2-\frac{l(l+1)}{x^2}\right\}R=0\\ \frac{d^{2}u}{d{x}^2}+\left\{2\epsilon -x^2-\frac{l(l+1)}{x^2}\right\}u=0\end{array}}$

Definimos, una nueva función v(x), calculamos la derivada primera y segunda de u respecto de x y las introducimos en la ecuación diferencial

${\displaystyle \begin{array}{l}u(x)=v(x)x^{l+1}\exp \left(-\frac{x^2}{2}\right)\\ \frac{du}{dx}=\frac{dv}{dx}{x}^{l+1}\exp \left(-\frac{x^2}{2}\right)+v\left(l+1\right)x^l\exp \left(-\frac{x^2}{2}\right)-v{x}^{l+2}\exp \left(-\frac{x^2}{2}\right)\\ \frac{d^{2}u}{d{x}^2}=\frac{d^{2}v}{d{x}^2}{x}^{l+1}\exp \left(-\frac{x^2}{2}\right)+\frac{dv}{dx}\left(l+1\right)x^l\exp \left(-\frac{x^2}{2}\right)-\frac{dv}{dx}{x}^{l+2}\exp \left(-\frac{x^2}{2}\right)\\ \frac{dv}{dx}\left(l+1\right)x^l\exp \left(-\frac{x^2}{2}\right)+vl\left(l+1\right)x^{l-1}\exp \left(-\frac{x^2}{2}\right)-v\left(l+1\right)x^{l+1}\exp \left(-\frac{x^2}{2}\right)\\ -\frac{dv}{dx}{x}^{l+2}\exp \left(-\frac{x^2}{2}\right)-v(l+2)x^{l+1}\exp \left(-\frac{x^2}{2}\right)+v{x}^{l+3}\exp \left(-\frac{x^2}{2}\right)\end{array}}$

Obtenemos la ecuación diferencial

${\displaystyle x\frac{d^{2}v}{d{x}^2}+\left(2\left(l+1\right)-2x^2\right)\frac{dv}{dx}+\left(2\epsilon -2l-3\right)x·v=0}$

Hacemos un nuevo cambio de variable, z=x²

${\displaystyle \begin{array}{l}\frac{dv}{dx}=\frac{dv}{dz}\frac{dz}{dx}=2x\frac{dv}{dz}\\ \frac{d^{2}v}{d{x}^2}=2\frac{dv}{dz}+2x\frac{d}{dx}\left(\frac{dv}{dz}\right)=2\frac{dv}{dz}+2x\frac{d}{dz}\left(\frac{dv}{dz}\right)\frac{dz}{dx}=2\frac{dv}{dz}+4x^2\frac{d^{2}v}{d{z}^2}\\ 2x\frac{dv}{dz}+4x^3\frac{d^{2}v}{d{z}^2}+\left(2\left(l+1\right)-2x^2\right)2x\frac{dv}{dz}+\left(2\epsilon -2l-3\right)x·v=0\\ z\frac{d^{2}v}{d{z}^2}+\left(l+\frac{1}{2}+1-z\right)\frac{dv}{dz}+\frac{1}{4}\left(2\epsilon -2l-3\right)v=0\\ z\frac{d^{2}v}{d{z}^2}+\left(l+\frac{1}{2}+1-z\right)\frac{dv}{dz}+\frac{1}{4}\left(2\left(k+\frac{3}{2}\right)-2l-3\right)v=0\\ z\frac{d^{2}v}{d{z}^2}+\left(l+\frac{1}{2}+1-z\right)\frac{dv}{dz}+\frac{k-l}{2}v=0\end{array}}$

Que es la ecuación diferencial de los polinomios asociados de Laguerre

${\displaystyle x\frac{d^{2}y}{d{x}^2}+(m+1-x)\frac{dy}{dx}+ny=\mathrm{0,}\{\begin{array}{l}m=l+\frac{1}{2}\\ n=\frac{k-l}{2}\end{array}}$

El coeficiente de y, n=(k-l)/2 tiene que ser un número entero positivo (incluyendo el cero), esto limita los posibles valores de l dado k

Dado el entero k, (energía del nivel, k+3/2) para que n sea entero, los posibles valores de l se recogen en la tabla. La última columna, nos da el índice inferior n de los polinomios asociados de Laguerre, m=l+1/2 es su índice superior

Partiendo de la solución de la ecuación diferencial de Laguerre, deshacemos los cambios hasta llegar a la expresión de la componente radial de la función de onda R(r)

${\displaystyle \begin{array}{l}v(x)=L_n^{l+\frac{1}{2}}(x^2)\\ u(x)=x^{l+1}\exp \left(-\frac{x^2}{2}\right)L_n^{l+\frac{1}{2}}(x^2)\\ R_{nl}(x)=C·x^l\exp \left(-\frac{x^2}{2}\right)L_n^{l+\frac{1}{2}}(x^2)\end{array}}$

La constante C se calcula de modo que

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^2{R}_{nl}^2(x)dx=1}\\ C^2{\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^{2l+2}\exp \left(-x^2\right){\left(L_n^{l+\frac{1}{2}}(x^2)\right)}^{2}dx=1}\end{array}}$

Recuérdese que el volumen de una capa comprendida entre las superficies esféricas concéntricas de radio x y x+dx es 4πx²·dx. Véase la página titulada El átomo de hidrógeno

Hacemos el cambio de variable z=x²

${\displaystyle \frac{C^2}{2}{\displaystyle \underset{0}{\overset{\infty }{\int }}{z}^{l+\frac{1}{2}}\exp \left(-z\right){\left(L_n^{l+\frac{1}{2}}(z)\right)}^{2}dz=1}}$

Teniendo en cuenta la relación de ortogonalidad de los polinomios asociados de Laguerre

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-x}{x}^k{L}_n^k(x)}{L}_m^k(x)dx=\{\begin{array}{l}\mathrm{0,}m\ne n\\ \frac{(n+k)!}{n!},m=n\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}\frac{C^2}{2}\frac{\left(n+l+\frac{1}{2}\right)!}{n!}=1\\ C=\sqrt{\frac{2n!}{\Gamma \left(n+l+1+\frac{1}{2}\right)}}\end{array}}$

Se ha utilizado la relación entre la función gamma, Γ(x) y el factorial de un número x!

${\displaystyle \left(n+\frac{1}{2}\right)!=\Gamma \left(n+1+\frac{1}{2}\right)}$

La componente radial de la función de onda R_nl(x)

${\displaystyle R_{nl}(x)=\sqrt{\frac{2n!}{\Gamma \left(n+l+1+\frac{1}{2}\right)}}·x^l\exp \left(-\frac{x^2}{2}\right)L_n^{l+\frac{1}{2}}(x^2)}$

Ejemplos

• R_1,1(x), energía, ε₃=3+3/2

k=3;
l=1;
n=1;
f=@(x) sqrt(2*factorial(n)/gamma(n+l+3/2))*x.^l.*exp(-x.^2/2).
*laguerreL(n, l+1/2, x.^2);
fplot(f,[0,5])
g=@(x) x.^2.*f(x).^2;
integral(g,0,20)
grid on
xlabel('x')
ylabel('R_{1,1}(x)')
title('Funciones radiales')



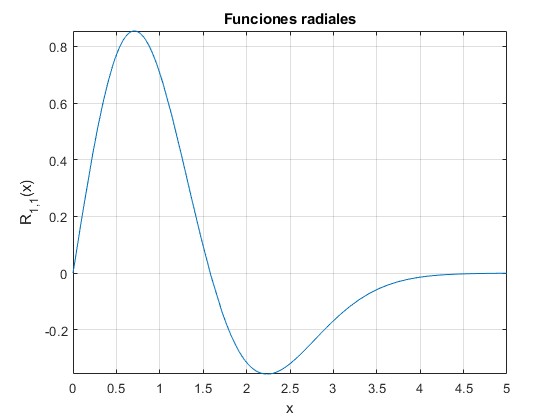
Comprobación

Se calcula mediante la función integral de MATLAB

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^2{R}_{nl}^2(x)dx}}$

>> g=@(x) x.^2.*f(x).^2;
>> integral(g,0,20)
>> 1.0000

• R_0,2(x), energía, ε₄=4+3/2

Se cambia la variable l=0, y la variable n=2



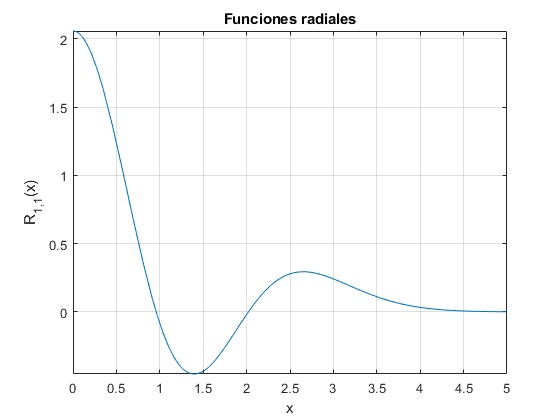
Comprobación

>> g=@(x) x.^2.*f(x).^2;
>> integral(g,0,20)
>> 1.0000

Referencias

3D Harmonic oscillator. January 19, 2018