La ecuación de Schrödinger en coordenadas esféricas

${\displaystyle \frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial \psi }{\partial r}\right)+\frac{1}{r^2\sin \theta }\frac{\partial }{\partial \theta }\left(\sin \theta \frac{\partial \psi }{\partial \theta }\right)+\frac{1}{r^2{\sin }^2\theta }\frac{{\partial }^2\psi }{\partial {\phi }^2}+\frac{2m}{{\hslash }^2}\left(E-V(r)\right)\psi =0}$

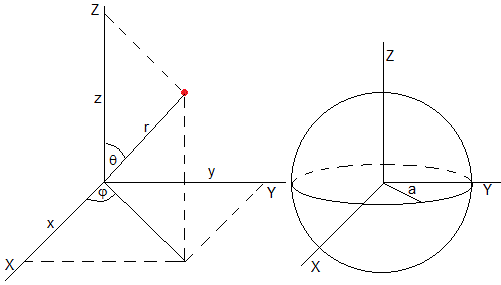
El potencial V(r) es

${\displaystyle V(r)=\{\begin{array}{l}\mathrm{0,}0\le r\le a\\ \infty ,r>a\end{array}}$

Para resolver la ecuación de Schrödinger transformaremos una ecuación diferencial en derivadas parciales en un sistema de tres ecuaciones diferenciales dependientes unicamente de las variables r, θ y φ, respectivamente

En primer lugar, supondremos que la solución de la ecuación de Schrödinger es el producto de dos funciones: una que describe el estado del electrón en la dirección radial r y otra en la dirección angular (θ, φ)

${\displaystyle \psi (r,\theta ,\phi )=R(r)·Y(\theta ,\phi )}$

Separamos la variable r de las variables θ y φ

${\displaystyle \begin{array}{l}Y\frac{d}{dr}\left(r^2\frac{dR}{dr}\right)+R\frac{1}{\sin \theta }\frac{\partial }{\partial \theta }\left(\sin \theta \frac{\partial Y}{\partial \theta }\right)+R\frac{1}{{\sin }^2\theta }\frac{{\partial }^{2}Y}{\partial {\phi }^2}+\frac{2m}{{\hslash }^2}{r}^2\left(E-V(r)\right)RY=0\\ \frac{1}{R}\frac{d}{dr}\left(r^2\frac{dR}{dr}\right)+\frac{2m}{{\hslash }^2}{r}^2\left(E-V(r)\right)=-\frac{1}{Y}\left\{\frac{1}{\sin \theta }\frac{\partial }{\partial \theta }\left(\sin \theta \frac{\partial Y}{\partial \theta }\right)+\frac{1}{{\sin }^2\theta }\frac{{\partial }^{2}Y}{\partial {\phi }^2}\right\}\end{array}}$

La parte izquierda no depende de (θ, φ) y la parte derecha no depende de r, por tanto, ambas términos se igualan a una constante que denominamos λ₁. La ecuación diferencial en derivadas parciales se transforma en el sistema de dos ecuaciones diferenciales

${\displaystyle \{\begin{array}{l}\frac{1}{r^2}\frac{d}{dr}\left(r^2\frac{dR}{dr}\right)+\left\{\frac{2m}{{\hslash }^2}\left(E-V(r)\right)-\frac{{\lambda }_1}{r^2}\right\}R=0\\ \frac{1}{\sin \theta }\frac{\partial }{\partial \theta }\left(\sin \theta \frac{\partial Y}{\partial \theta }\right)+\frac{1}{{\sin }^2\theta }\frac{{\partial }^{2}Y}{\partial {\phi }^2}+{\lambda }_{1}Y=0\end{array}}$

La parte angular

Supondremos que la solución Y(θ, φ) de la segunda ecuación diferencial en derivadas parciales es el producto de dos funciones que dependen solamente de θ y φ, respectivamente

${\displaystyle \begin{array}{l}Y(\theta ,\phi )=\Theta (\theta )\Phi (\phi )\\ \frac{\Phi }{\sin \theta }\frac{d}{d\theta }\left(\sin \theta \frac{d\Theta }{d\theta }\right)+\frac{\Theta }{{\sin }^2\theta }\frac{d^2\Phi }{d{\phi }^2}+{\lambda }_1\Theta \Phi =0\\ \frac{\sin \theta }{\Theta }\frac{d}{d\theta }\left(\sin \theta \frac{d\Theta }{d\theta }\right)+{\lambda }_1{\sin }^2\theta =-\frac{1}{\Phi }\frac{d^2\Phi }{d{\phi }^2}\end{array}}$

La ecuación de la izquierda solamente depende de θ y la de la derecha solamente depende de φ, por lo que ambos lados se igualan a la constante λ₂, quedando un sistema de dos ecuaciones diferenciales

${\displaystyle \{\begin{array}{l}\frac{1}{\sin \theta }\frac{d}{d\theta }\left(\sin \theta \frac{d\Theta }{d\theta }\right)+\left({\lambda }_1-\frac{{\lambda }_2}{{\sin }^2\theta }\right)\Theta =0\\ \frac{d^2\Phi }{d{\phi }^2}+{\lambda }_2\Phi =0\end{array}}$

Las condiciones de contorno determinan los valores permitidos para λ₁ y λ₂

Solución en φ

La última ecuación diferencial es la más sencilla de resolver, en la mayor parte de los casos, se requiere una solución real

${\displaystyle \Phi (\phi )=\{\begin{array}{l}A\cos \left(\sqrt{{\lambda }_2}\phi \right)+B\sin \left(\sqrt{{\lambda }_2}\phi \right),{\lambda }_2\ne 0\\ C+D\phi ,{\lambda }_2=0\end{array}}$

En este caso, esta restricción no es necesaria

${\displaystyle \Phi (\phi )=A\exp \left(i\sqrt{{\lambda }_2}\phi \right)+B\exp \left(-i\sqrt{{\lambda }_2}\phi \right)}$

La solución es periódica, $\Phi (\phi +2\pi )=\Phi (\phi )$. Igualando la parte real y la parte imaginaria, obtenemos

${\displaystyle \begin{array}{l}\{\begin{array}{l}A\cos \left(\sqrt{{\lambda }_2}\left(\phi +2\pi \right)\right)+B\cos \left(\sqrt{{\lambda }_2}\left(\phi +2\pi \right)\right)=A\cos \left(\sqrt{{\lambda }_2}\phi \right)+B\cos \left(\sqrt{{\lambda }_2}\phi \right)\\ A\sin \left(\sqrt{{\lambda }_2}\left(\phi +2\pi \right)\right)-B\sin \left(\sqrt{{\lambda }_2}\left(\phi +2\pi \right)\right)=A\sin \left(\sqrt{{\lambda }_2}\phi \right)-B\sin \left(\sqrt{{\lambda }_2}\phi \right)\end{array}\\ \{\begin{array}{l}\left(A+B\right)\cos \left(\sqrt{{\lambda }_2}\left(\phi +2\pi \right)\right)=\left(A+B\right)\cos \left(\sqrt{{\lambda }_2}\phi \right)\\ \left(A-B\right)\sin \left(\sqrt{{\lambda }_2}\left(\phi +2\pi \right)\right)=\left(A-B\right)\sin \left(\sqrt{{\lambda }_2}\phi \right)\end{array}\end{array}}$

Si A≠B y A+B≠0 entonces $\sqrt{{\lambda }_2}$ tiene que ser un entero.

${\displaystyle m=\sqrt{{\lambda }_2},\mathrm{0,}\pm \mathrm{1,}\pm \mathrm{2,}\pm \mathrm{3...}}$

La solución de esta parte angular se expresa de la forma

${\displaystyle \Phi (\phi )=\exp (im\phi ),m=\mathrm{0,}\pm \mathrm{1,}\pm \mathrm{2....}}$

Solución en θ

Buscamos la solución de la ecuación diferencial en θ

${\displaystyle \frac{d^2\Theta }{d{\theta }^2}+\frac{\cos \theta }{\sin \theta }\frac{d\Theta }{d\theta }+\left({\lambda }_1-\frac{m^2}{{\sin }^2\theta }\right)\Theta =0}$

Hacemos un cambio de variable y denominamos y(x)=Θ(θ)

${\displaystyle \begin{array}{l}x=\cos \theta ,\frac{dx}{d\theta }=-\sin \theta \\ \frac{d\Theta }{d\theta }=\frac{dy}{dx}\frac{dx}{d\theta }=-\sin \theta \frac{dy}{dx}\\ \frac{d^2\Theta }{d{\theta }^2}=\frac{d}{d\theta }\left(\frac{d\Theta }{d\theta }\right)=\frac{d}{d\theta }\left(-\sin \theta \frac{dy}{dx}\right)=-\cos \theta \frac{dy}{dx}-\sin \theta \frac{d}{d\theta }\left(\frac{dy}{dx}\right)=\\ -\cos \theta \frac{dy}{dx}-\sin \theta \frac{d}{dx}\left(\frac{dy}{dx}\right)\frac{dx}{d\theta }=-\cos \theta \frac{dy}{dx}+{\sin }^2\theta \frac{d^{2}y}{d{x}^2}=\left(1-x^2\right)\frac{d^{2}y}{d{x}^2}-x\frac{dy}{dx}\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}\left(1-x^2\right)\frac{d^{2}y}{d{x}^2}-x\frac{dy}{dx}-x\frac{dy}{dx}+\left({\lambda }_1-\frac{m^2}{1-x^2}\right)y=0\\ \left(1-x^2\right)\frac{d^{2}y}{d{x}^2}-2x\frac{dy}{dx}+\left(l(l+1)-\frac{m^2}{1-x^2}\right)y=0\end{array}}$

Cuando m=0, obtenemos la ecuación de Legendre

Esta ecuación diferencial se denomina asociada de Legendre. Los polinomios asociados de Legendre se calculan

${\displaystyle P_{l,m}(x)={\left(-1\right)}^m\sqrt{{\left(1-x^2\right)}^m}\frac{d^m}{d{x}^m}{P}_l(x)}$

Polinomios de Legendre

Los primeros polinomios de Legendre son

${\displaystyle \begin{array}{l}{P}_0(x)=1\hfill \\ P_1(x)=x\hfill \\ P_2(x)=\frac{1}{2}(3x^2-1)\hfill \\ P_3(x)=\frac{1}{2}(5x^3-3x)\hfill \\ P_4(x)=\frac{1}{8}(35x^4-30x^2+3)\hfill \\ P_5(x)=\frac{1}{8}(63x^5-70x^3+15x)\hfill \\ P_6(x)=\frac{1}{16}(231x^6-315x^4+105x^2-5)\hfill \\ P_7(x)=\frac{1}{16}(429x^7-693x^5+315x^3-35x)\hfill \\ \mathrm{.....}\hfill \end{array}}$

Los primeros polinomios asociados de Legendre son

${\displaystyle \begin{array}{l}{P}_{\mathrm{0,0}}(x)=P_0(x)=1\\ P_{\mathrm{1,0}}(x)=P_1(x)=x\\ P_{\mathrm{1,1}}(x)=\left(-1\right)\sqrt{1-x^2}\frac{d}{dx}{P}_1(x)=-\sqrt{\left(1-x^2\right)}\\ P_{\mathrm{2,0}}(x)=P_2(x)=\frac{1}{2}(3x^2-1)\\ P_{\mathrm{2,1}}(x)=\left(-1\right)\sqrt{1-x^2}\frac{d}{dx}{P}_2(x)=-3x\sqrt{\left(1-x^2\right)}\\ P_{\mathrm{2,2}}(x)={\left(-1\right)}^2\sqrt{{\left(1-x^2\right)}^2}\frac{d^2}{d{x}^2}{P}_2(x)=3\left(1-x^2\right)\\ P_{\mathrm{3,0}}(x)=P_3(x)=\frac{1}{2}(5x^3-3x)\\ P_{\mathrm{3,1}}(x)=\left(-1\right)\sqrt{1-x^2}\frac{d}{dx}{P}_3(x)=-\frac{3}{2}(5x^2-1)\sqrt{\left(1-x^2\right)}\\ P_{\mathrm{3,2}}(x)={\left(-1\right)}^2\sqrt{{\left(1-x^2\right)}^2}\frac{d^2}{d{x}^2}{P}_3(x)=15x\left(1-x^2\right)\\ P_{\mathrm{3,3}}(x)={\left(-1\right)}^3\sqrt{{\left(1-x^2\right)}^3}\frac{d^3}{d{x}^3}{P}_3(x)=-15{\left(1-x^2\right)}^{3/2}\end{array}}$

Se generan mediante el siguiente código MATLAB, por ejmplo, para l=3 y m=2

syms x;
l=3;
m=2;
y=(-1)^m*(1-x^2)^(m/2)*diff(legendreP(l,x),m);
y=simplify(y)

y =15*x*(1 - x^2)

P_l(x) es un polinomio de grado l, la derivada es distinta de cero si m≤l. Los posibles valores del número entero m=0, ±1, ±2, ±3,... ±l, en total 2l+1

Solución de la ecuación diferencial

La solución de la parte angular de la ecuación de Schrödinger se denomina armónicos esféricos

${\displaystyle \begin{array}{l}{Y}_{l,m}\left(\theta ,\phi \right)={\left(-1\right)}^m\sqrt{\frac{(2l+1)}{4\pi }\frac{(l-m)!}{(l+m)!}}{P}_{l.m}\left(\cos \theta \right)e^{im\phi },m\ge 0\\ Y_{l,-m}\left(\theta ,\phi \right)=Y_{{}_{l,m}}^{*}\left(\theta ,\phi \right),m<0\end{array}}$

Para números enteros m negativos se hace el mismo cálculo que para m positivo, solamente cambia el signo delante del exponente del número e, imφ

Estas funciones satisfacen la relación de ortonormalidad

${\displaystyle {\displaystyle \underset{0}{\overset{\pi }{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{Y}_{l,m}\left(\theta ,\phi \right)·Y_{{}_{l\text{'},m\text{'}}}^{*}\left(\theta ,\phi \right)\sin \theta ·d\theta ·d\phi ={\delta }_{l,l\text{'}}}}{\delta }_{m,m\text{'}}}$

El elemento diferencial de área de una esfera de radio unidad es, sinθ·dθ·dφ

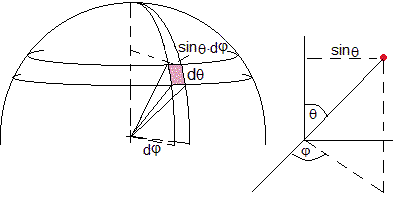
Los primeros armónicos esféricos son

${\displaystyle \begin{array}{l}{Y}_{\mathrm{0,0}}\left(\theta ,\phi \right)=\frac{1}{2\sqrt{\pi }}\\ Y_{\mathrm{1,0}}\left(\theta ,\phi \right)=\frac{1}{2}\sqrt{\frac{3}{\pi }}\cos \theta \\ Y_{\mathrm{1,}\pm 1}\left(\theta ,\phi \right)=\left(-1\right)\sqrt{\frac{3}{4\pi }\frac{1}{2!}}\left(-\sin \theta \right)e^{\pm i\phi }=\frac{1}{2}\sqrt{\frac{3}{2\pi }}\sin \theta ·e^{\pm i\phi }\\ Y_{\mathrm{2,0}}\left(\theta ,\phi \right)=\sqrt{\frac{5}{4\pi }\frac{2!}{2!}}\frac{1}{2}(3{\cos }^2\theta -1)=\frac{1}{4}\sqrt{\frac{5}{\pi }}(3{\cos }^2\theta -1)\\ Y_{\mathrm{2,}\pm 1}\left(\theta ,\phi \right)=\left(-1\right)\sqrt{\frac{5}{4\pi }\frac{1!}{3!}}\left(-3\cos \theta ·\sin \theta \right)e^{\pm i\phi }=\frac{1}{2}\sqrt{\frac{15}{2\pi }}\cos \theta ·\sin \theta ·e^{\pm i\phi }\\ Y_{\mathrm{2,}\pm 2}\left(\theta ,\phi \right)={\left(-1\right)}^2\sqrt{\frac{5}{4\pi }\frac{1}{4!}}3{\sin }^2\theta ·e^{\pm i2\phi }=\frac{1}{4}\sqrt{\frac{15}{2\pi }}{\sin }^2\theta ·e^{\pm i2\phi }\\ Y_{\mathrm{3,0}}\left(\theta ,\phi \right)=\sqrt{\frac{7}{4\pi }\frac{3!}{3!}}\frac{1}{2}(5{\cos }^3\theta -3\cos \theta )=\frac{1}{4}\sqrt{\frac{7}{\pi }}(5{\cos }^3\theta -3\cos \theta )\\ Y_{\mathrm{3,}\pm 1}\left(\theta ,\phi \right)=\left(-1\right)\sqrt{\frac{7}{4\pi }\frac{2!}{4!}}\left(-\frac{3}{2}(5{\cos }^2\theta -1)\sin \theta \right)e^{\pm i\phi }=\frac{1}{8}\sqrt{\frac{21}{\pi }}(5{\cos }^2\theta -1)\sin \theta ·e^{\pm i\phi }\\ Y_{\mathrm{3,}\pm 2}\left(\theta ,\phi \right)={\left(-1\right)}^2\sqrt{\frac{7}{4\pi }\frac{1!}{5!}}15\cos \theta {\sin }^2\theta ·e^{\pm i2\phi }=\frac{1}{4}\sqrt{\frac{105}{2\pi }}\cos \theta {\sin }^2\theta ·e^{\pm i2\phi }\\ Y_{\mathrm{3,}\pm 3}\left(\theta ,\phi \right)={\left(-1\right)}^3\sqrt{\frac{7}{4\pi }\frac{1}{6!}}\left(-15{\sin }^3\theta \right)e^{\pm i3\phi }=\frac{1}{8}\sqrt{\frac{35}{\pi }}{\sin }^3\theta ·e^{\pm i3\phi }\end{array}}$

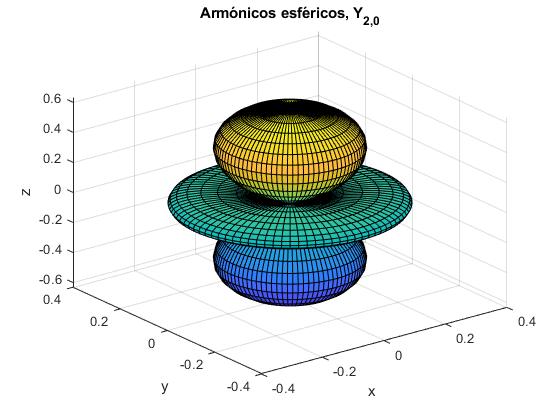
Representamos Y_2,0(θ)

theta=linspace(0,pi,45);
phi=linspace(0,2*pi,90);
[theta,phi]=meshgrid(theta,phi);

r=(3*cos(theta).^2-1)*sqrt(5/pi)/4; %Y(2,0)
x=r.*cos(phi).*sin(theta);
y=r.*sin(phi).*sin(theta);
z=r.*cos(theta);

surf(x,y,z)
xlabel('x'); ylabel('y'); zlabel('z')
title('Armónicos esféricos, Y_{2,0}')

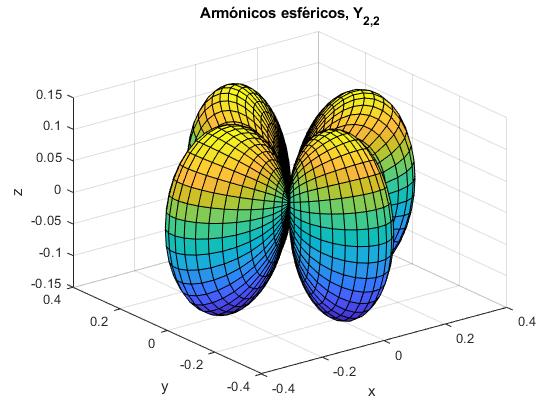
Representamos la parte real de Y_2,2(θ, φ)

theta=linspace(0,pi,45);
phi=linspace(0,2*pi,90);
[theta,phi]=meshgrid(theta,phi);

r=(sin(theta).^2).*cos(2*phi)*sqrt(15/(2*pi))/4; %real Y(2,2)
x=r.*cos(phi).*sin(theta);
y=r.*sin(phi).*sin(theta);
z=r.*cos(theta);

surf(x,y,z)
xlabel('x'); ylabel('y'); zlabel('z')
title('Armónicos esféricos, Y_{2,2}')

La parte radial

La ecuación diferencial de la parte radial es

${\displaystyle \frac{1}{r^2}\frac{d}{dr}\left(r^2\frac{dR}{dr}\right)+\left\{\frac{2m}{{\hslash }^2}\left(E-V(r)\right)-\frac{l(l+1)}{r^2}\right\}R=0}$

La función de onda es nula en exterior de la esfera. La ecuación de Schrödinger en el interior, V (r)=0, es

${\displaystyle \frac{d}{dr}\left(r^2\frac{dR}{dr}\right)+\left\{\frac{2mE}{{\hslash }^2}{r}^2-l(l+1)\right\}R=0}$

Haciendo el cambio de variable, u=r·R(r)

${\displaystyle \begin{array}{l}R=\frac{u}{r},\frac{dR}{dr}=\left(r\frac{du}{dr}-u\right)\frac{1}{r^2}\\ \frac{d}{dr}\left(r^2\frac{dR}{dr}\right)=r\frac{d^{2}u}{d{r}^2}\end{array}}$

obtenemos la ecuación diferencial

${\displaystyle \frac{d^{2}u}{d{r}^2}+\left\{k^2-\frac{l(l+1)}{r^2}\right\}u=\mathrm{0,}{k}^2=\frac{2mE}{{\hslash }^2}}$

Vamos a resolver esta ecuación diferencial con la condición de contorno u(a)=0.

Caso particular: l=0

El caso más simple, se presenta cuando l=0

${\displaystyle \begin{array}{l}\frac{d^{2}u}{d{r}^2}+k^{2}u=0\\ u=A\sin (kr)+B\cos (kr)\\ R(r)=A\frac{\sin (kr)}{r}+B\frac{\cos (kr)}{r}\end{array}}$

Cuando r→0, el cociente cos(kr)/r tiende a infinito, por lo que se descarta este término, haciendo B=0

${\displaystyle R(r)=A\frac{\sin (kr)}{r}}$

Cuando r=a, R(a)=0. por lo que ka=nπ.

Los niveles de energía son

${\displaystyle E_{n\mathrm{,0}}=\frac{{\hslash }^2{\pi }^2}{2m{a}^2}{n}^2,n=\mathrm{1,2,3...}}$

la misma que para un pozo de potencial unidimensional de anchura a. En la página titulada Pozo de potencial, se obtiene los niveles de energía de una partícula en un pozo de potencial de profundidad infinita de anchura 2a

La parte radial de la función de onda es

${\displaystyle R_{n\mathrm{,0}}(r)=\frac{A}{r}\sin \left(n\pi \frac{r}{a}\right)}$

El coeficiente A se determina haciendo que

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{a}{\int }}{r}^2{R}_{n\mathrm{,0}}^2(r)·dr}=1\\ A^2{\displaystyle \underset{0}{\overset{a}{\int }}\frac{1-\cos \left(2n\pi \frac{r}{a}\right)}{2}dr=1}\\ \frac{A^2}{2}a=1\end{array}}$

Por tanto, la parte radial de la función de onda para l=0 es

${\displaystyle R_{n\mathrm{,0}}(r)=\sqrt{\frac{2}{a}}\frac{1}{r}\sin \left(n\pi \frac{r}{a}\right)}$

Combinamos la parte radial y angular

${\displaystyle {\psi }_{n\mathrm{,0,0}}(r,\theta ,\phi )=R_{n\mathrm{,0}}(r)Y_{\mathrm{0,0}}\left(\theta ,\phi \right)=\frac{1}{\sqrt{2\pi a}}\frac{1}{r}\sin \left(n\pi \frac{r}{a}\right)}$

Caso general, l≠0

Vamos a buscar la solución de la ecuación diferencial

${\displaystyle \frac{d^{2}u}{d{r}^2}+\left\{k^2-\frac{l(l+1)}{r^2}\right\}u=0}$

Llamamos ρ=kr, la ecuación diferencial se transforma en

${\displaystyle \begin{array}{l}{k}^2\frac{d^{2}u}{d{\rho }^2}+\left\{k^2-k^2\frac{l(l+1)}{{\rho }^2}\right\}u=0\\ {\rho }^2\frac{d^{2}u}{d{\rho }^2}+\left\{{\rho }^2-l(l+1)\right\}u=0\end{array}}$

Hacemos el cambio de variable, u=ρv

${\displaystyle \begin{array}{l}\frac{du}{d\rho }=v+\rho \frac{dv}{d\rho }\\ \frac{d^{2}u}{d{\rho }^2}=2\frac{dv}{d\rho }+\rho \frac{d^{2}v}{d{\rho }^2}\end{array}}$

La ecuación diferencial se transforma en

${\displaystyle \begin{array}{l}{\rho }^2\left\{2\frac{dv}{d\rho }+\rho \frac{d^{2}v}{d{\rho }^2}\right\}+\left\{{\rho }^2-l(l+1)\right\}\rho v=0\\ {\rho }^2\frac{d^{2}v}{d{\rho }^2}+2\rho \frac{dv}{d\rho }+\left({\rho }^2-l(l+1)\right)v=0\end{array}}$

La solución es (Véase en la página titulada Funciones de Bessel el apartado, Funciones esféricas de Bessel)

${\displaystyle \begin{array}{l}v(\rho )=A·j_l(\rho )+B·y_l(\rho )\\ u(r)=Ar·j_l(kr)+Br·y_l(kr)\\ R(r)=A·j_l(kr)+B·y_l(kr)\end{array}}$

j_l(x) es la función esférica de Bessel de orden l e y_l(x) es la función esférica de Neumann de orden l. Se definen en términos de las funciones de Bessel

${\displaystyle j_l(x)=\sqrt{\frac{\pi }{2x}}{J}_{l+\frac{1}{2}}(x),y_l(x)=\sqrt{\frac{\pi }{2x}}{Y}_{l+\frac{1}{2}}(x)}$

La función, y_l(x) tiene de a infinito cuando x→0 por lo que hay que descartar este término, haciendo B=0

${\displaystyle R(r)=A{j}_l(kr)}$

La función de onda se anula para r=a, j_l(ka)=0

function esferico
    xx=linspace(0,20,10);
    for l=0:3
        f=@(x) sqrt(pi./(2*x)).*besselj(l+1/2,x);
        beta=raices(f,xx);
        disp([l,beta])
    end
             
    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

         0    3.1416    6.2832    9.4248   12.5664   15.7080   18.8496
    1.0000    4.4934    7.7253   10.9041   14.0662   17.2208
    2.0000    5.7635    9.0950   12.3229   15.5146   18.6890
    3.0000    6.9879   10.4171   13.6980   16.9236

Denominamos β_n,l a la raíz n de j_l(ka)=0. Los niveles de energía son

${\displaystyle \begin{array}{l}k=\frac{{\beta }_{nl}}{a}\\ E_{nl}=\frac{{\hslash }^2{\beta }_{nl}^2}{2m{a}^2}\end{array}}$

La parte radial de la función de onda es

${\displaystyle R_{n,l}(r)=A·j_l\left({\beta }_{n,l}\frac{r}{a}\right)}$

El coeficiente A se determina haciendo que

${\displaystyle {\displaystyle \underset{0}{\overset{a}{\int }}{r}^2{R}_{n,l}^2\left({\beta }_{n,l}\frac{r}{a}\right)·dr}=1}$

El volumen de una capa esférica comprendida entre r y r+dr es 4πr²·dr

Utilizando las propiedades de las funciones de Bessel

${\displaystyle \begin{array}{l}{A}^2{\displaystyle \underset{0}{\overset{a}{\int }}{r}^2\frac{\pi }{2{\beta }_{n,l}\frac{r}{a}}{J}_{l+\frac{1}{2}}^2\left({\beta }_{n,l}\frac{r}{a}\right)·dr}=1\\ A^2\frac{\pi }{2{\beta }_{n,l}}{a}^3{\displaystyle \underset{0}{\overset{1}{\int }}x{J}_{l+\frac{1}{2}}^2\left({\beta }_{n,l}x\right)·dx}=1\\ A^2\frac{\pi }{4{\beta }_{n,l}}{a}^3{J}_{{}_{l+\frac{3}{2}}}^2\left({\beta }_{n,l}\right)=1\end{array}}$

Representamos la función de onda radial R(r) de los primeros niveles n de energía, para l=0

function esferico_1
    a=1;    
    l=0; %cambiar a l=1,2,3...
    f=@(x) sqrt(pi./(2*x)).*besselj(l+1/2,x);
    xx=linspace(0,10,10);
    rr=raices(f,xx);
    disp(rr);
    hold on
    for k=rr
       A=2*sqrt(k)/sqrt(pi*a^3*besselj(l+3/2,k)^2);
       f1=@(x) A*sqrt(pi./(2*k*x)).*besselj(l+1/2,k*x);
        fplot(f1,[0,a])
    end
    hold off
    xlabel('r/a')
    ylabel('R(r)')
    grid on
    title('Funciones de onda, l=0')

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

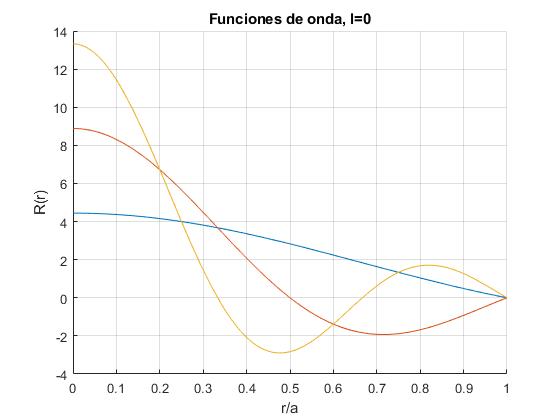
3.1416    6.2832    9.4248

Representamos la función de onda radial R(r) de los primeros niveles n de energía, para l=1

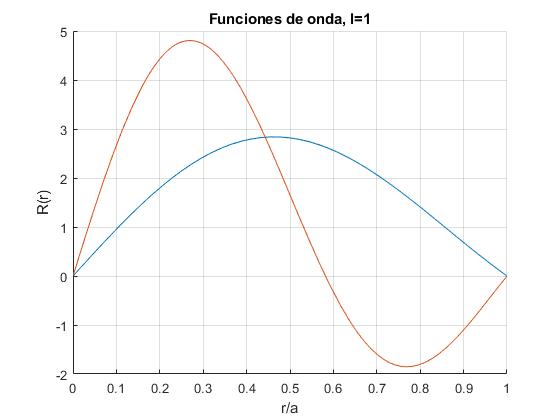
4.4934    7.7253

Finalmente, combinamos la solución radial y angular

${\displaystyle {\psi }_{n,l,m}(r,\theta ,\phi )=A\sin \left({\beta }_{n,l}\frac{r}{a}\right)Y_{l,m}(\theta ,\phi )}$

Para cada valor de l hay 2l+1 valores de m con la misma energía

Referencias

David J. Griffiths. Introduction to Quantum Mechanics. Edt. Prentice Hall (1995), pp. 129-132