Polinomios de Laguerre

Los primeros polinomios de Laguerre son.

${\displaystyle \begin{array}{l}{L}_0(x)=1\\ L_1(x)=1-x\\ L_2(x)=\frac{1}{2!}\left(2-4x+x^2\right)\\ L_3(x)=\frac{1}{3!}\left(6-18x+9x^2-x^3\right)\\ L_4(x)=\frac{1}{4!}\left(24-96x+72x^2-16x^3+x^4\right)\\ L_5(x)=\frac{1}{5!}\left(120-600x+600x^2-200x^3+24x^4-x^5\right)\\ L_6(x)=\frac{1}{6!}\left(720-4320x+5400x^2-2400x^3+450x^4-36x^5+x^6\right)\end{array}}$

Utilizamos la función laguerreL de MATLAB para mostrar los primeros polinomios de Laguerre

>> syms x;
>> for n=0:6
laguerreL(n,x)
end
 
ans =1
ans =1 - x
ans =x^2/2 - 2*x + 1
ans =- x^3/6 + (3*x^2)/2 - 3*x + 1
ans =x^4/24 - (2*x^3)/3 + 3*x^2 - 4*x + 1
ans =- x^5/120 + (5*x^4)/24 - (5*x^3)/3 + 5*x^2 - 5*x + 1
ans =x^6/720 - x^5/20 + (5*x^4)/8 - (10*x^3)/3 + (15*x^2)/2 - 6*x + 1

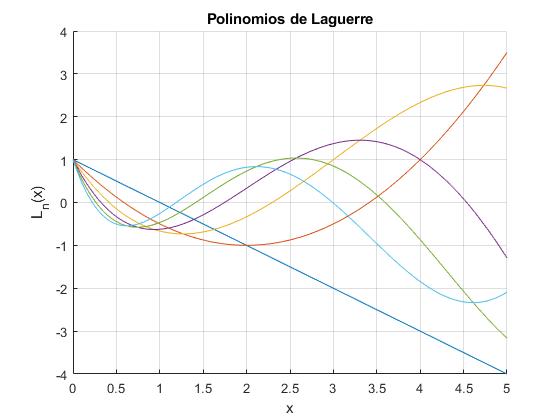
Representamos gráficamente los polinomios de L₁(x) a L₆(x) empleando el comando fplot.

hold on
for n=1:6
    fplot(@(x) laguerreL(n,x),[0,5]);
end
hold off
grid on
xlabel('x')
ylabel('L_n(x)')
title('Polinomios de Laguerre')

Utilizamos la relación de recurrencia para crear una función recursiva laguerre para obtener los valores L_n(x),

function res=laguerre(n,x) %n=2,3,4...
   if n==0
        res=1;
    elseif n==1
        res=1-x;
    else
        res=((2*n-1-x).*laguerre(n-1,x)-(n-1)*laguerre(n-2,x))/n;
   end
end

Llamamos a la función laguerre para n=3

>> syms x;
>> laguerre(3,x)
ans =(2*x)/3 - ((((x - 1)*(x - 3))/2 - 1/2)*(x - 5))/3 - 2/3
>> expand(ans)
ans =- x^3/6 + (3*x^2)/2 - 3*x + 1

Otra forma de obtener los polinomios de Laguerre es

${\displaystyle L_n(x)=1+{\displaystyle \sum _{k=1}^n\left(\begin{array}{c}n\\ k\end{array}\right)\frac{{\left(-1\right)}^k}{k!}}{x}^k=n!{\displaystyle \sum _{k=0}^n\frac{{\left(-1\right)}^k}{(n-k){\left(!k\right)}^2}{x}^k}}$

function res=laguerre_4(n)
    syms x;
    res=1;
    for k=1:n
        res=res+x^k*nchoosek(n,k)*(-1)^k/factorial(k);
    end
end

Llamamos a la función laguerre_4 y también a laguerreL de MATLAB, para comprobar que se obtiene el mismo resultado

>> laguerre_4(3)
ans =- x^3/6 + (3*x^2)/2 - 3*x + 1
>> laguerreL(3,x)
ans =- x^3/6 + (3*x^2)/2 - 3*x + 1

De otra forma

syms x k;
for n=0:6
    pol=factorial(n)*symsum((-1)^k*x^k/(factorial(n-k)*factorial(k)^2),k,0,n)
end

pol =1
pol =1 - x
pol =x^2/2 - 2*x + 1
pol =- x^3/6 + (3*x^2)/2 - 3*x + 1
pol =x^4/24 - (2*x^3)/3 + 3*x^2 - 4*x + 1
pol =- x^5/120 + (5*x^4)/24 - (5*x^3)/3 + 5*x^2 - 5*x + 1
pol =x^6/720 - x^5/20 + (5*x^4)/8 - (10*x^3)/3 + (15*x^2)/2 - 6*x + 1

Definimos una función que calcula los coeficientes del polinomio de Laguerre de grado n

function p=laguerre_p(n)
    p=zeros(n+1,1);
    p1=zeros(n,1);
    p0=zeros(n-1,1);
    format rat;
%valores iniciales   
    p0=[1];
    p1=[-1 1];
   if n==0
       p=p0;
   elseif n==1
        p=p1;
   else
        for k=2:n
            p=((2*k-1)*[0 p1]-[p1 0]-(k-1)*[0 0 p0])/k;
            p0=p1;
            p1=p;
        end
   end
end

La función poly2sym convierte el vector de los coeficientes en un polinomio simbólico p(x)

>> syms x;
>> L4=poly2sym(laguerre_p(4))
L4 =x^4/24 - (2*x^3)/3 + 3*x^2 - 4*x + 1
>> L5=poly2sym(laguerre_p(5))
L5 =- x^5/120 + (5*x^4)/24 - (5*x^3)/3 + 5*x^2 - 5*x + 1

Mediante la función polyval de MATLAB, se calcula el valor del polinomio de Laguerre para un valor de x o para un vector de datos x

>> polyval(laguerre_p(4),2)
ans =       1/3     
>> laguerreL(4,2)
ans =       1/3   

Propiedades

• En la gráfica vemos que

L_n(0)=1

• Ortogonalidad

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-x}{L}_m(x)L_n(x)dx=\{\begin{array}{l}\mathrm{0,}m\ne n\\ \mathrm{1,}m=n\end{array}}}$

>> syms x;
>> int(exp(-x)*laguerreL(4,x)*laguerreL(5,x),x,0,inf)
ans =0
>> int(exp(-x)*laguerreL(5,x)*laguerreL(5,x),x,0,inf)
ans =1

• Derivada

${\displaystyle x\frac{d}{dx}{L}_n(x)=n{L}_n(x)-n{L}_{n-1}(x)}$

>> syms x;
>> n=3;
>> x*diff(laguerreL(n,x))
ans =-x*(x^2/2 - 3*x + 3)
>> n*laguerreL(n,x)-n*laguerreL(n-1,x)
ans =- x^3/2 + 3*x^2 - 3*x

Polinomio p(x) de grado n

${\displaystyle $ \begin{array}{l}1=L_0\\ x=L_0-L_1\\ x^2=2L_0-4L_1+2L_2\\ x^3=6L_0-18L_1+18L_2-6L_3\\ x^4=24L_0-96L_1+144L_2-96L_3+24L_4\\ x^5=120L_0-600L_1+1200L_2-1200L_3+600L_4-120L_5\\ x^6=720L_0-4320L_1+10800L_2-1440L_3+10800L_4-4320L_5+720L_6\end{array}$}$

Una potencia xⁿ se puede expresar como una combinación lineal de n+1 polinomios de Laguerre L_k(x), k=0, 1, 2...n, Los coeficientes valen

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^n{e}^{-x}{L}_k(x)dx}={\left(-1\right)}^k\left(\begin{array}{c}n\\ k\end{array}\right)n!,k=\mathrm{0,1,2...}n}$

function res=potencia(n)
    syms x;
    res=zeros(1,n+1);
    for k=0:n
        res(k+1)=int(exp(-x)*x^n*laguerreL(k,x),x,0,inf);
    end
end

Por ejemplo, para x³ y x⁵

>> potencia(3)
ans =    6   -18    18    -6
>> potencia(5)
ans =    120        -600        1200       -1200         600        -120

Alternativamente

function res=potencia_1(n)
    res=zeros(1,n+1);
    for k=0:n
        res(k+1)=(-1)^k*nchoosek(n,k)*factorial(n);
    end
 end

Definida esta función, podemos expresar cualquier polinomio p(x) en términos de los polinomios de Lagerre L_k(x)

function res=polinomio(pol)
    res=zeros(1,length(pol));
    for n=0:length(pol)-1
        for k=0:n
             res(k+1)=res(k+1)+(-1)^k*nchoosek(n,k)*factorial(n)*pol(length(pol)-n);
        end  
    end
 end

El polinomio 2x³+4x²+2x+1, se expresa como una combinación lineal de los polinomios de Laguerre, a₀L₀(x)+a₁L₁(x)+a₂L₂(x)+a₃L₃(x). Los coeficientes valen

>> polinomio([2,4,2,1])
ans =    23   -54    44   -12

Comprobación

>> 23*laguerreL(0,x)-54*laguerreL(1,x)+44*laguerreL(2,x)-12*laguerreL(3,x)
ans =2*x^3 + 4*x^2 + 2*x + 1

Polinomios asociados de Laguerre

La ecuación diferencial y su solución, los polinomios asociados de Laguerre, son

${\displaystyle \begin{array}{l}x\frac{d^{2}y}{d{x}^2}+\left(m+1-x\right)\frac{dy}{dx}+ny=0\\ L_n^m(x)={\left(-1\right)}^m\frac{d^m}{d{x}^m}{L}_{m+n}(x)=(n+m)!{\displaystyle \sum _{k=0}^n\frac{{\left(-1\right)}^k}{(n-k)!(k+m)!k!}{x}^k}\end{array}}$

Generamos el polinomio asociado $L_2^3(x)$ con el siguiente código

syms x k;
n=2;
m=3;
pol=symsum((-1)^k*factorial(n+m)*x^k/(factorial(n+m-k)*factorial(k)^2),k,0,n+m);
pol_n_m=(-1)^m*diff(pol,m)
pol1_n_m=factorial(n+m)*symsum((-1)^k*x^k/(factorial(n-k)*factorial(m+k)*
factorial(k)),k,0,n)

pol_n_m =x^2/2 - 5*x + 10
pol1_n_m =x^2/2 - 5*x + 10

Generamos los polinomios asociados $L_n^m(x)$ con el siguiente código

syms x k;
for n=0:3
    for m=0:n
        disp([n,m])
        pol_n_m=factorial(n+m)*symsum((-1)^k*x^k/(factorial(n-k)*
factorial(m+k)*factorial(k)),k,0,n)
    end
end

      0     0    pol_n_m =1
      1     0    pol_n_m =1 - x
      1     1    pol_n_m =2 - x
      2     0    pol_n_m =x^2/2 - 2*x + 1
      2     1    pol_n_m =x^2/2 - 3*x + 3
      2     2    pol_n_m =x^2/2 - 4*x + 6
      3     0    pol_n_m =- x^3/6 + (3*x^2)/2 - 3*x + 1
      3     1    pol_n_m =- x^3/6 + 2*x^2 - 6*x + 4
      3     2    pol_n_m =- x^3/6 + (5*x^2)/2 - 10*x + 10
      3     3    pol_n_m =- x^3/6 + 3*x^2 - 15*x + 20

${\displaystyle \begin{array}{l}{L}_0^0(x)=1\\ L_1^0(x)=1-x\\ L_1^1(x)=2-x\\ L_2^0(x)=\frac{1}{2}{x}^2-2x+1\\ L_2^1(x)=\frac{1}{2}{x}^2-3x+3\\ L_2^2(x)=\frac{1}{2}{x}^2-4x+6\end{array}}$

Dado n, los polinomios asociados de Laguerre para distintos valores de m son

${\displaystyle \begin{array}{l}{L}_0^m(x)=1\\ L_1^m(x)=-x+m+1\\ L_2^m(x)=\frac{1}{2}\left(x^2-2(m+2)x+(m+1)(m+2)\right)\\ L_3^m(x)=\frac{1}{6}\left(-x^3+3(m+3)x^2-3(m+2)(m+3)x+(m+1)(m+2)(m+3)\right)\end{array}}$

Utilizando la función laguerreL de MATLAB

>> syms m x;
>> laguerreL(1,m,x)
ans =m - x + 1
>> laguerreL(2,m,x)
ans =(3*m)/2 - x*(m + 2) + m^2/2 + x^2/2 + 1
>> laguerreL(3,m,x)
ans =(11*m)/6 - x*(m^2/2 + (5*m)/2 + 3) + x^2*(m/2 + 3/2) + m^2 + m^3/6 - x^3/6 + 1

Propiedades

Relaciones de recurrencia

${\displaystyle n{L}_n^m(x)=\left(2n+m-1-x\right)L_{n-1}^m(x)-\left(n+m-1\right)L_{n-2}^m(x),n=\mathrm{2,3,4...}}$

function res=laguerre_a(n,m, x) %n=2,3,4...
   if n==0
        res=1;
    elseif n==1
        res=-x+m+1;
    else
        res=((2*n+m-1-x).*laguerre_a(n-1,m, x)-(n+m-1)*laguerre_a(n-2,m, x))/n;
   end
end

>> syms x;
>> m=2;
>> n=2;
>> laguerre_a(n,m,x)
ans =((x - 3)*(x - 5))/2 - 3/2
>> expand(ans)
ans =x^2/2 - 4*x + 6

Relaciones de ortogonalidad

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-x}{x}^k{L}_n^k(x)}{L}_m^k(x)dx=\{\begin{array}{l}\mathrm{0,}m\ne n\\ \frac{(n+k)!}{n!},m=n\end{array}}$

Comprobación

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-x}{x}^2{L}_2^2(x)}{L}_3^2(x)dx=0\\ {\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-x}{x}^2{\left(L_2^2(x)\right)}^2}dx=\frac{(2+2)!}{2!}=12\\ {\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-x}{x}^2{\left(L_3^2(x)\right)}^2}dx=\frac{(3+2)!}{3!}=20\end{array}}$

syms x;
k=2;
f_2=(x^2-2*(k+2)*x+(k+1)*(k+2))/2;
f_3=(-x^3+3*(k+3)*x^2-3*(k+2)*(k+3)*x+(k+1)*(k+2)*(k+3))/6;
int(exp(-x)*x^k*f_2*f_3,x,0,inf)
int(exp(-x)*x^k*f_2^2,x,0,inf)
int(exp(-x)*x^k*f_3^2,x,0,inf)

ans =0
ans =12
ans =20 

Alternativamente, utilizando la función laguerreL de MATLAB

syms x;
k=2;
int(exp(-x)*x^k*laguerreL(2,k,x)*laguerreL(3,k,x),x,0,inf)
int(exp(-x)*x^k*laguerreL(2,k,x)^2,x,0,inf)
int(exp(-x)*x^k*laguerreL(3,k,x)^2,x,0,inf)

Polinomios de Hermite

Los primeros polinomios de Hermite son.

${\displaystyle \begin{array}{l}{H}_0(x)=1\\ H_1(x)=2x\\ H_2(x)=4x^2-2\\ H_3(x)=8x^3-12x\\ H_4(x)=16x^4-48x^2+12\\ H_5(x)=32x^5-160x^3+120x\\ H_6(x)=64x^6-480x^4+720x^2-120\\ H_7(x)=128x^7-1334x^5+3360x^3-1680x\end{array}}$

Utilizamos la función hermiteH de MATLAB para mostrar los primeros polinomios de hermite

>> syms x;
>> for n=0:6
hermiteH(n,x)
end
 
ans =1 
ans =2*x
ans =4*x^2 - 2
ans =8*x^3 - 12*x
ans =16*x^4 - 48*x^2 + 12
ans =32*x^5 - 160*x^3 + 120*x
ans =64*x^6 - 480*x^4 + 720*x^2 - 120

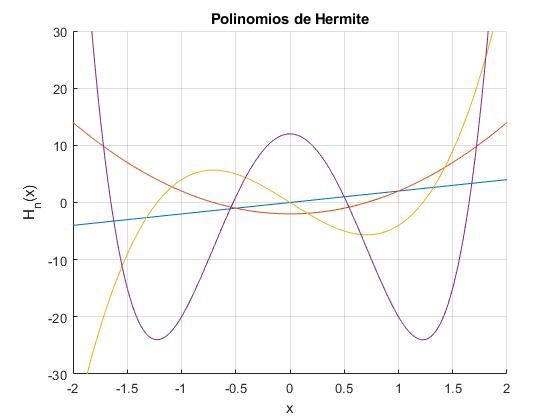
Representamos gráficamente los polinomios de H₁(x) a H₄(x) empleando el comando fplot.

hold on
for n=1:4
    fplot(@(x) hermiteH(n,x),[-2,2]);
end
hold off
grid on
ylim([-30,30])
xlabel('x')
ylabel('H_n(x)')
title('Polinomios de Hermite')

Utilizamos la relación de recurrencia para crear una función recursiva hermite para obtener los valores H_n(x),

function res=hermite(n,x) %n=2,3,4...
   if n==0
        res=1;
    elseif n==1
        res=2*x;
    else
        res=2*x.*hermite(n-1,x)-2*(n-1)*hermite(n-2,x);
    end
end

Llamamos a la función hermite y también a hermiteH de MATLAB, para comprobar que se obtiene el mismo resultado

>> hermite(4,5)
ans =        8812
>> hermiteH(4,5)
ans =        8812

Definimos una función que calcula los coeficientes del polinomio de Hermite de grado n

function p=hermite_p(n)
    p=zeros(n+1,1);
    p1=zeros(n,1);
    p0=zeros(n-1,1);
%valores iniciales   
    p0=[1];
    p1=[2 0];
   if n==0
       p=p0;
   elseif n==1
        p=p1;
   else
        for k=2:n
            p=2*[p1 0]-2*(k-1)*[0 0 p0];
            p0=p1;
            p1=p;
        end
   end
end

La función poly2sym convierte el vector de los coeficientes en un polinomio simbólico p(x)

>> syms x;
>> H4=poly2sym(hermite_p(4))
H4 =16*x^4 - 48*x^2 + 12
>> H5=poly2sym(hermite_p(5))
H5 =32*x^5 - 160*x^3 + 120*x

Mediante la función polyval de MATLAB, se calcula el valor del polinomio de Hermite para un valor de x o para un vector de datos x

>> polyval(hermite_p(4),2)
ans =    76
>> hermiteH(4,2)
ans =    76

Propiedades

• En la gráfica vemos que las funciones son

• Simétricas, índice n par
• Antisimétricas, índice n impar

${\displaystyle H_n(x)={\left(-1\right)}^n{H}_n(-x)}$

• Valor para x=0 y n par

${\displaystyle H_{2n}(0)={\left(-1\right)}^n\frac{(2n)!}{n!}}$

>> n=4;
>> (-1)^n*factorial(2*n)/factorial(n)
ans = 1680
>> hermiteH(2*n,0)
ans =     1680

>> n=3;
>> (-1)^n*factorial(2*n)/factorial(n)
ans =  -120
>> hermiteH(2*n,0)
ans =  -120

• Derivadas

${\displaystyle \frac{d}{dx}{H}_n(x)=2n{H}_{n-1}(x)}$

>> syms x;
>> n=4;
>> diff(hermiteH(n,x))
ans =64*x^3 - 96*x
>> 2*n*hermiteH(n-1,x)
ans =64*x^3 - 96*x 

• Ortogonalidad

${\displaystyle {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{e}^{-x^2}{H}_n(x)}{H}_m(x)dx=\{\begin{array}{l}\sqrt{\pi }{2}^{n}n!,m=n\\ \mathrm{0,}m\ne n\end{array}}$

Para n=4 el resultado es $384\sqrt{\pi }$. Para n=4 y m=5, el resultado es cero

>> syms x;
>> n=4;
>> int(exp(-x^2)*hermiteH(n,x)^2,x,-inf,inf)
ans =384*pi^(1/2)
>> int(exp(-x^2)*hermiteH(n,x)*hermiteH(n+1,x),x,-inf,inf)
ans =0

Ejemplos en el curso de Física

El oscilador armónico cuántico

El oscilador armónico en dos dimensiones

El oscilador armónico en tres dimensiones

El átomo de hidrógeno

Potencial de Morse y potencial de Pöschl–Teller

El átomo de hidrógeno en en dos dimensiones

Referencias

Alan Jeffrey, Hui-Hui Dai. Handbook of Mathematical Formulas and Integrals. Elsevier (2008). págs. 325-332