El átomo de hidrógeno en dos dimensiones

El átomo de hidrógeno en en dos dimensiones

Resolveremos la ecuación de Schrödinger independiente del tiempo en coordenadas polares, para el potencial V(r)=-e²/(4πε₀r). Donde e es la carga del electrón, m_e su masa, y r es la distancia al núcleo (protón)

$- \frac{ℏ^{2}}{2 m_{e}} (\frac{1}{r} \frac{\partial}{\partial r} (r \frac{\partial ψ (r, φ)}{\partial r}) + \frac{1}{r^{2}} \frac{\partial^{2} ψ (r, φ)}{\partial φ^{2}}) - \frac{e^{2}}{4 π ε_{0} r} ψ (r, φ) = E ψ (r, φ)$

Intentamos la separación de variables

$\begin{array}{l} ψ (r, φ) = R (r) \cdot Φ (φ) \\ \frac{Φ}{r} \frac{d}{d r} (r \frac{d R}{d r}) + \frac{R}{r^{2}} \frac{d^{2} Φ}{d φ^{2}} + \frac{2 m_{e}}{ℏ^{2}} (E + \frac{e^{2}}{4 π ε_{0} r}) R Φ = 0 \\ \frac{r}{R} \frac{d}{\partial r} (r \frac{d R}{d r}) + \frac{2 m_{e}}{ℏ^{2}} (E + \frac{e^{2}}{4 π ε_{0} r}) r^{2} = - \frac{1}{Φ} \frac{d^{2} Φ}{d φ^{2}} \end{array}$

El primer término, solamente depende de r, el segundo de φ, la ecuación diferencial se transforma en el sistema de dos ecuaciones diferenciales

$\begin{array}{l} {\begin{cases} \frac{r}{R} \frac{d}{d r} (r \frac{d R}{d r}) + \frac{2 m_{e}}{ℏ^{2}} (E + \frac{e^{2}}{4 π ε_{0} r}) r^{2} = m^{2} \\ - \frac{1}{Φ} \frac{d^{2} Φ}{d φ^{2}} = m^{2} \end{cases} \\ {\begin{cases} \frac{d^{2} R}{d r^{2}} + \frac{1}{r} \frac{d R}{d r} + {\frac{2 m_{e}}{ℏ^{2}} (E + \frac{e^{2}}{4 π ε_{0} r}) - \frac{m^{2}}{r^{2}}} R = 0 \\ \frac{d^{2} Φ}{d φ^{2}} + m^{2} Φ = 0 \end{cases} \end{array}$

La ecuación angular

Tiene una solución conocida, que expresamos de forma equivalente

$Φ (φ) = C_{1} \exp (i m φ) + C_{2} \exp (- i m φ)$

La solución es periódica, Φ(φ+2π)=Φ(φ). Igualando las partes real e imaginaria

$\begin{array}{l} {\begin{cases} C_{1} \cos (m φ + 2 π n_{φ}) + C_{2} \cos (m φ + 2 π n_{φ}) = C_{1} \cos (m φ) + C_{2} \cos (m φ) \\ C_{1} \sin (m φ + 2 π m) - C_{2} \sin (m φ + 2 π m) = C_{1} \sin (m φ) - C_{2} \sin (m φ) \end{cases} \\ {\begin{cases} (C_{1} + C_{2}) \cos (m φ + 2 π m) = (C_{1} + C_{2}) \cos (m φ) \\ (C_{1} - C_{2}) \sin (m φ + 2 π m) = (C_{1} - C_{2}) \sin (m φ) \end{cases} \end{array}$

Si C₁≠C₂ y C₁+ C₂≠0, entonces m tiene que ser un entero.

$Φ (φ) = C \exp (i m φ), m = 0, \pm 1, \pm 2....$

La ecuación radial

Hacemos el cambio de variable

$E = - \frac{m_{e} e^{4}}{2 ℏ^{2} {(4 π ε_{0})}^{2}} \frac{1}{N^{2}}, r = N \frac{ℏ^{2} (4 π ε_{0})}{2 m_{e} e^{2}} x$

Obtenemos una ecuación diferencial en términos de la variable x

$\begin{array}{l} \frac{m_{e}^{2} e^{4}}{ℏ^{4} {(4 π ε_{0})}^{2}} \frac{4}{N^{2}} {\frac{d^{2} R}{d x^{2}} + \frac{1}{x} \frac{d R}{d x}} + {- \frac{m_{e}^{2} e^{4}}{ℏ^{4} {(4 π ε_{0})}^{2}} \frac{1}{N^{2}} + \frac{4}{N} \frac{m_{e}^{2} e^{4}}{ℏ^{4} {(4 π ε_{0})}^{2}} \frac{1}{x} - \frac{4}{N^{2}} \frac{m_{e}^{2} e^{4}}{ℏ^{4} {(4 π ε_{0})}^{2}} \frac{m^{2}}{x^{2}}} R = 0 \\ \frac{d^{2} R}{d x^{2}} + \frac{1}{x} \frac{d R}{d x} + (- \frac{1}{4} + \frac{N}{x} - \frac{m^{2}}{x^{2}}) R = 0 \end{array}$

Definimos

$R (x) = x^{| m |} \exp (- \frac{x}{2}) G (x)$

Calculamos la derivada primera y segunda de R respecto de x

$\begin{array}{l} \frac{d R}{d x} = | m | x^{| m | - 1} \exp (- \frac{x}{2}) G (x) - \frac{1}{2} x^{| m |} \exp (- \frac{x}{2}) G (x) + x^{| m |} \exp (- \frac{x}{2}) \frac{d G (x)}{d x} \\ = (\frac{| m |}{x} - \frac{1}{2}) x^{| m |} \exp (- \frac{x}{2}) G (x) + x^{| m |} \exp (- \frac{x}{2}) \frac{d G (x)}{d x} \\ \frac{d^{2} R}{d x^{2}} = - \frac{| m |}{x^{2}} x^{| m |} \exp (- \frac{x}{2}) G (x) + (\frac{| m |}{x} - \frac{1}{2}) | m | x^{| m | - 1} \exp (- \frac{x}{2}) G (x) - \frac{1}{2} (\frac{| m |}{x} - \frac{1}{2}) x^{| m |} \exp (- \frac{x}{2}) G (x) \\ + (\frac{| m |}{x} - \frac{1}{2}) x^{| m |} \exp (- \frac{x}{2}) \frac{d G (x)}{d x} + | m | x^{| m | - 1} \exp (- \frac{x}{2}) \frac{d G (x)}{d x} - \frac{1}{2} x^{| m |} \exp (- \frac{x}{2}) \frac{d G (x)}{d x} + x^{| m |} \exp (- \frac{x}{2}) \frac{d^{2} G (x)}{d x^{2}} \end{array}$

Obtenemos una ecuación diferencial en G

$\begin{array}{l} x^{| m |} \exp (- \frac{x}{2}) \frac{d^{2} G (x)}{d x^{2}} + {(2 | m | + 1) x^{| m | - 1} - x^{| m |}} \exp (- \frac{x}{2}) \frac{d G (x)}{d x} + {N - (\frac{1}{2} + | m |)} x^{| m | - 1} \exp (- \frac{x}{2}) G (x) = 0 \\ x \frac{d^{2} G (x)}{d x^{2}} + {(2 | m | + 1) - x} \frac{d G (x)}{d x} - {- N + (\frac{1}{2} + | m |)} G (x) = 0 \end{array}$

Es una ecuación del tipo

$z \frac{d^{2} w}{d z^{2}} + (b - z) \frac{d w}{d z} - a w = 0$

que se denomina hipergeométrica confluente, cuya solución es

$G (x) = {}_{1}F_{1} (a; b, x) = {}_{1}F_{1} (- N + | m | + \frac{1}{2}; 2 | m | + 1, x)$

La solución que satisface la condición en el infinito es la siguiente: el argumento a=-N+|m|+1/2 deberá ser un número entero negativo (o cero). Dado que |m| es un entero,

$N = \frac{1}{2}, \frac{3}{2}, \frac{5}{2} ....$

La función hipergeométrica se reduce a polinomios asociados de Laguerre de grado -a

Sea

$n = N + \frac{1}{2} = 1,2,3,4....$

n se denomina número cuántico principal. Para un valor dado de n, |m| toma los valores,

$| m | = 0, 1, 2, 3,... n - 1$

Los niveles de energía se obtienen mediante la fórmula

$E_{n} = - \frac{m_{e} e^{4}}{2 ℏ^{2} {(4 π ε_{0})}^{2}} \frac{1}{{(n - \frac{1}{2})}^{2}}, n = 1,2,3,4...$

Las funciones de onda radiales R_nm(r) son

$\begin{array}{l} R_{n m} (r) = \frac{β_{n}}{(2 | m |)!} \sqrt{\frac{(n + | m | - 1)!}{(2 n - 1) (n - | m | - 1)!}} {(β_{n} r)}^{| m |} \exp (- \frac{β_{n}}{2} r) {}_{1}F_{1} (- n + | m | + 1; 2 | m | + 1, β_{n} r) \\ β_{n} = \frac{2}{n - \frac{1}{2}} \frac{m_{e} e^{2}}{(4 π ε_{0}) ℏ^{2}} = \frac{2}{n - \frac{1}{2}} \frac{1}{a_{0}} \end{array}$

Siendo a₀ el radio de Bohr

Esta función hipergeométrica está relacionada con los polinomios asociados de Laguerre del siguiente modo

$L_{n}^{m} (z) = \frac{(n + m)!}{n! m!} {}_{1}F_{1} (- n; m + 1, z)$

Funciones radiales R_nm(r)

R₁₀(r)

$\begin{array}{l} R_{10} (r) = \frac{β_{1}}{(2 \cdot 0)!} \sqrt{\frac{(1 + 0 - 1)!}{(2 \cdot 1 - 1) (1 - 0 - 1)!}} {(β_{1} r)}^{0} \exp (- \frac{β_{1}}{2} r) {}_{1}F_{1} (- 1 + 0 + 1; 2 \cdot 0 + 1, β_{1} r) \\ R_{10} (r) = β_{1} \exp (- \frac{β_{1}}{2} r) {}_{1}F_{1} (0; 1, β_{1} r) \\ β_{1} = \frac{4}{a_{0}} \\ {}_{1}F_{1} (0; 0 + 1, β_{1} r) = \frac{0! 0!}{(0 + 0)!} L_{0}^{0} (β_{1} r) = 1 \\ R_{10} (r) = β_{1} \exp (- \frac{β_{1}}{2} r) \end{array}$

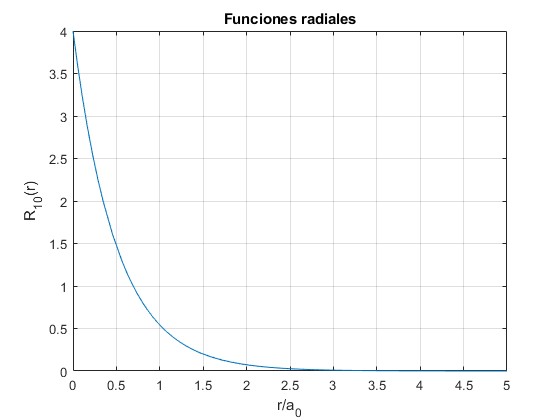
Representamos R₁₀(r) en función de r/a₀

beta=4;
f=@(x) beta*exp(-beta*x/2);
fplot(f,[0,5])
grid on
xlabel('r/a_0')
ylabel('R_{10}(r)')
title('Funciones radiales')

R₂₀(r)

$\begin{array}{l} R_{20} (r) = \frac{β_{2}}{(2 \cdot 0)!} \sqrt{\frac{(2 + 0 - 1)!}{(2 \cdot 2 - 1) (2 - 0 - 1)!}} {(β_{2} r)}^{0} \exp (- \frac{β_{2}}{2} r) {}_{1}F_{1} (- 2 + 0 + 1; 2 \cdot 0 + 1, β_{2} r) \\ R_{20} (r) = \frac{1}{\sqrt{3}} β_{2} \exp (- \frac{β_{2}}{2} r) {}_{1}F_{1} (- 1; 1, β_{2} r) \\ β_{2} = \frac{4}{3} \frac{1}{a_{0}} \\ {}_{1}F_{1} (- 1; 0 + 1, β_{2} r) = \frac{1! 0!}{(1 + 0)!} L_{1}^{0} (β_{2} r) = 1 - β_{2} r \\ R_{20} (r) = \frac{1}{\sqrt{3}} β_{2} \exp (- \frac{β_{2}}{2} r) (1 - β_{2} r) \end{array}$

R₂₁(r)

$\begin{array}{l} R_{21} (r) = \frac{β_{2}}{(2 \cdot 1)!} \sqrt{\frac{(2 + 1 - 1)!}{(2 \cdot 2 - 1) (2 - 1 - 1)!}} {(β_{2} r)}^{1} \exp (- \frac{β_{2}}{2} r) {}_{1}F_{1} (- 2 + 1 + 1; 2 \cdot 1 + 1, β_{2} r) \\ R_{21} (r) = \frac{β_{2}}{2} \sqrt{\frac{2}{3}} (β_{2} r) \exp (- \frac{β_{2}}{2} r) {}_{1}F_{1} (0; 3, β_{2} r) \\ {}_{1}F_{1} (0; 2 + 1, β_{2} r) = \frac{0! 2!}{(0 + 2)!} L_{0}^{2} (β_{2} r) = 1 \\ R_{21} (r) = \frac{β_{2}^{2}}{\sqrt{6}} r \exp (- \frac{β_{2}}{2} r) \end{array}$

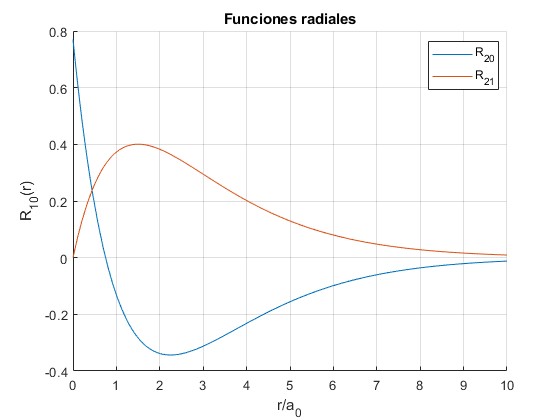
beta=4/3;
hold on
f0=@(x) beta*exp(-beta*x/2).*(1-beta*x)/sqrt(3);
fplot(f0,[0,10])
f1=@(x) beta^2*exp(-beta*x/2).*x/sqrt(6);
fplot(f1,[0,10])
hold off
grid on
legend('R_{20}','R_{21}','Location','best')
xlabel('r/a_0')
ylabel('R_{10}(r)')
title('Funciones radiales')

R₃₀(r)

$\begin{array}{l} R_{30} (r) = \frac{β_{3}}{(2 \cdot 0)!} \sqrt{\frac{(3 + 0 - 1)!}{(2 \cdot 3 - 1) (3 - 0 - 1)!}} {(β_{3} r)}^{0} \exp (- \frac{β_{3}}{2} r) {}_{1}F_{1} (- 3 + 0 + 1; 2 \cdot 0 + 1, β_{3} r) \\ R_{30} (r) = \frac{β_{3}}{5} \exp (- \frac{β_{3}}{2} r) {}_{1}F_{1} (- 2; 2, β_{3} r) \\ β_{3} = \frac{4}{5} \frac{1}{a_{0}} \\ {}_{1}F_{1} (- 2; 0 + 1, β_{3} r) = \frac{2! 0!}{(2 + 0)!} L_{2}^{0} (β_{2} r) = \frac{1}{2} {(β_{2} r)}^{2} - 2 β_{2} r + 1 \\ R_{30} (r) = \frac{β_{3}}{\sqrt{5}} \exp (- \frac{β_{3}}{2} r) (\frac{1}{2} {(β_{2} r)}^{2} - 2 β_{2} r + 1) \end{array}$

R₃₁(r)

$\begin{array}{l} R_{31} (r) = \frac{β_{3}}{(2 \cdot 1)!} \sqrt{\frac{(3 + 1 - 1)!}{(2 \cdot 3 - 1) (3 - 1 - 1)!}} {(β_{3} r)}^{1} \exp (- \frac{β_{3}}{2} r) {}_{1}F_{1} (- 3 + 1 + 1; 2 \cdot 1 + 1, β_{3} r) \\ R_{31} (r) = \frac{β_{3}}{2} \sqrt{\frac{6}{5}} (β_{3} r) \exp (- \frac{β_{3}}{2} r) {}_{1}F_{1} (- 1; 3, β_{3} r) \\ {}_{1}F_{1} (- 1; 2 + 1, β_{3} r) = \frac{1! 2!}{(1 + 2)!} L_{1}^{2} (β_{2} r) = \frac{1}{3} (- β_{2} r + 3) \\ R_{31} (r) = \frac{β_{3}^{2} r}{\sqrt{30}} \exp (- \frac{β_{3}}{2} r) (- β_{2} r + 3) \end{array}$

R₃₂(r)

$\begin{array}{l} R_{32} (r) = \frac{β_{3}}{(2 \cdot 2)!} \sqrt{\frac{(3 + 2 - 1)!}{(2 \cdot 3 - 1) (3 - 2 - 1)!}} {(β_{3} r)}^{2} \exp (- \frac{β_{3}}{2} r) {}_{1}F_{1} (- 3 + 2 + 1; 2 \cdot 2 + 1, β_{3} r) \\ R_{32} (r) = \frac{β_{3}}{4 \cdot 3 \cdot 2} \sqrt{\frac{4 \cdot 3 \cdot 2}{5}} {(β_{3} r)}^{2} \exp (- \frac{β_{3}}{2} r) {}_{1}F_{1} (0; 5, β_{3} r) \\ {}_{1}F_{1} (0; 4 + 1, β_{3} r) = \frac{0! 4!}{(0 + 4)!} L_{0}^{4} (β_{2} r) = 1 \\ R_{32} (r) = \frac{β_{3}^{2}}{\sqrt{120}} r^{2} \exp (- \frac{β_{3}}{2} r) \end{array}$

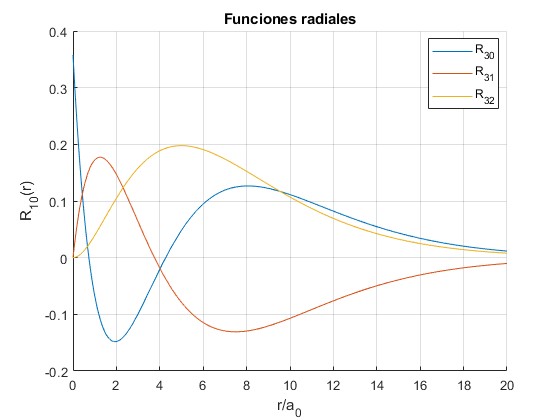
beta=4/5;
hold on
f0=@(x) beta*exp(-beta*x/2).*(beta^2*x.^2/2-2*beta*x+1)/sqrt(5);
fplot(f0,[0,20])
f1=@(x) beta^2*exp(-beta*x/2).*x.*(-beta*x+3)/sqrt(30);
fplot(f1,[0,20])
f2=@(x) beta^2*exp(-beta*x/2).*(x.^2)/sqrt(120);
fplot(f2,[0,20])
hold off
grid on
xlabel('r/a_0')
legend('R_{30}','R_{31}','R_{32}','Location','best')
ylabel('R_{10}(r)')
title('Funciones radiales')

Comprobamos que las funciones radiales están normalizadas

La integral

$\int_{0}^{\infty} R_{n m}^{2} (r) (2 π r \cdot d r) = 1$

también

$\int_{0}^{\infty} r R_{n m}^{2} (r) \cdot d r = 1$

Teniendo en cuenta el resultado de las integrales

$\begin{array}{l} {\int_{0}^{\infty} e^{- β r} d r = - \frac{e^{- β r}}{β} |}_{0}^{\infty} = \frac{1}{β} \\ {\int_{0}^{\infty} r e^{- β r} d r = - \frac{r}{β} e^{- β r} |}_{0}^{\infty} + \frac{1}{β} \int_{0}^{\infty} e^{- β r} d r = \frac{1}{β^{2}} \\ {\int_{0}^{\infty} r^{2} e^{- β r} d r = - \frac{r^{2}}{β} e^{- β r} |}_{0}^{\infty} + \frac{2}{β} \int_{0}^{\infty} r e^{- β r} d r = \frac{2}{β} \frac{1}{β^{2}} = \frac{2}{β^{3}} \\ {\int_{0}^{\infty} r^{3} e^{- β r} d r = - \frac{r^{3}}{β} e^{- β r} |}_{0}^{\infty} + \frac{3}{β} \int_{0}^{\infty} r^{2} e^{- β r} d r = \frac{3}{β} \frac{2}{β^{3}} = \frac{6}{β^{4}} \\ {\int_{0}^{\infty} r^{4} e^{- β r} d r = - \frac{r^{4}}{β} e^{- β r} |}_{0}^{\infty} + \frac{4}{β} \int_{0}^{\infty} r^{3} e^{- β r} d r = \frac{4}{β} \frac{6}{β^{4}} = \frac{4!}{β^{5}} \\ {\int_{0}^{\infty} r^{n} e^{- β r} d r = - \frac{r^{n}}{β} e^{- β r} |}_{0}^{\infty} + \frac{n}{β} \int_{0}^{\infty} r^{n - 1} e^{- β r} d r = \frac{n!}{β^{n + 1}} \end{array}$

Comprobamos

$\begin{array}{l} \int_{0}^{\infty} r R_{10}^{2} (r) d r = β_{1}^{2} \int_{0}^{\infty} r e^{- β_{1} r} d r = β_{1}^{2} \frac{1!}{β_{1}^{2}} = 1 \\ \int_{0}^{\infty} r R_{20}^{2} (r) d r = \frac{β_{2}^{2}}{3} \int_{0}^{\infty} r e^{- β_{2} r} {(1 - β_{2} r)}^{2} d r = \frac{β_{2}^{2}}{3} {\int_{0}^{\infty} r e^{- β_{2} r} d r + β_{2}^{2} \int_{0}^{\infty} r^{3} e^{- β_{2} r} d r - 2 β_{2} \int_{0}^{\infty} r^{2} e^{- β_{2} r} d r} = \\ \frac{β_{2}^{2}}{3} {\frac{1!}{β_{2}^{2}} + β_{2}^{2} \frac{3!}{β_{2}^{4}} - 2 β_{2} \frac{2!}{β_{2}^{3}}} = 1 \\ \int_{0}^{\infty} r R_{21}^{2} (r) d r = \frac{β_{2}^{4}}{6} \int_{0}^{\infty} r^{3} e^{- β_{2} r} d r = \frac{β_{2}^{4}}{6} \frac{3!}{β_{2}^{4}} = 1 \\ \int_{0}^{\infty} r R_{31}^{2} (r) d r = \frac{β_{3}^{4}}{30} \int_{0}^{\infty} r^{3} e^{- β_{2} r} {(3 - β_{3} r)}^{2} d r = \frac{β_{3}^{4}}{30} {9 \int_{0}^{\infty} r^{3} e^{- β_{2} r} d r - 6 β_{3} \int_{0}^{\infty} r^{4} e^{- β_{2} r} d r + β_{3}^{2} \int_{0}^{\infty} r^{5} e^{- β_{2} r} d r} = \\ \frac{β_{3}^{4}}{30} {9 \frac{3!}{β_{3}^{4}} - 6 β_{3} \frac{4!}{β_{3}^{5}} + β_{3}^{2} \frac{5!}{β_{3}^{6}}} = 1 \end{array}$

Referencias

X. L. Yang, S. H. Guo, F. T. Chan. Analytic solution of a two-dimensional hydrogen atom. Nonrelativistic theory. Physical Review A, Vol. 43, n. 3, 1 February 1991, pp. 1186-1196

La ecuación angular

La ecuación radial

Funciones radiales Rnm(r)

Referencias

Funciones radiales R_nm(r)