La ecuación de Schrödinger en la dirección radial es

${\displaystyle \frac{1}{r^2}\frac{d}{dr}\left(r^2\frac{dR}{dr}\right)+\left\{\frac{2m}{{\hslash }^2}\left(E-V(r)\right)-\frac{l(l+1)}{r^2}\right\}R=0}$

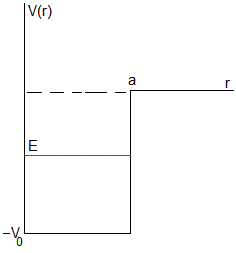
donde V(r) es el potencial

${\displaystyle V(r)=\{\begin{array}{l}-V_0,0\le r\le a\\ \mathrm{0,}r>a\end{array}}$

Tenemos que resolver dos ecuaciones diferenciales, una para el interior de la esfera de radio a y otra, para el exterior. En r=a la componente radial de la función de onda R(r) deberá ser continua y también su derivada primera. Lo que nos permitirá calcular los niveles de energía E_n dado el valor del número l

${\displaystyle \{\begin{array}{l}\frac{1}{r^2}\frac{d}{dr}\left(r^2\frac{dR}{dr}\right)+\left\{\frac{2m}{{\hslash }^2}\left(E+V_0\right)-\frac{l(l+1)}{r^2}\right\}R=\mathrm{0,}0\le r\le a\\ \frac{1}{r^2}\frac{d}{dr}\left(r^2\frac{dR}{dr}\right)+\left\{\frac{2m}{{\hslash }^2}E-\frac{l(l+1)}{r^2}\right\}R=\mathrm{0,}r>a\end{array}}$

Haciendo el cambio de variable, u=rR(r),

${\displaystyle \begin{array}{l}R=\frac{u}{r}\\ \frac{dR}{dr}=\left(r\frac{du}{dr}-u\right)\frac{1}{r^2},\frac{d}{dr}\left(r^2\frac{dR}{dr}\right)=r\frac{d^{2}u}{d{r}^2}\end{array}}$

Las ecuaciones diferenciales se transforman en

${\displaystyle \{\begin{array}{l}\frac{d^{2}u}{d{r}^2}+\left\{q^2-\frac{l(l+1)}{r^2}\right\}u=\mathrm{0,}{q}^2=\frac{2m}{{\hslash }^2}\left(E+V_0\right),0\le r\le a\\ \frac{d^{2}u}{d{r}^2}+\left\{-k^2-\frac{l(l+1)}{r^2}\right\}u=\mathrm{0,}{k}^2=-\frac{2m}{{\hslash }^2}E,r>a\end{array}}$

k²>0 y q²>0 ya que los niveles de energía E_n se encuentran en el intervalo -V₀<E_n<0

Caso particular: l=0

El caso más sencillo se presenta cuando l=0

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{d^{2}u}{d{r}^2}+q^{2}u=\mathrm{0,}{q}^2=\frac{2m}{{\hslash }^2}\left(E+V_0\right),0\le r\le a\\ \frac{d^{2}u}{d{r}^2}-k^{2}u=\mathrm{0,}{k}^2=-\frac{2m}{{\hslash }^2}E,r>a\end{array}\\ q^2=\frac{2m}{{\hslash }^2}\left(E+V_0\right)=-k^2+\frac{2m}{{\hslash }^2}{V}_0\end{array}}$

• La solución de la primera ecuación diferencial, para r≤a, es

${\displaystyle \begin{array}{l}u(r)=A\sin \left(qr\right)+B\cos \left(qr\right)\\ R(r)=A\frac{\sin \left(qr\right)}{r}+B\frac{\cos \left(qr\right)}{r}\end{array}}$

Cuando r→0, el primer término de R(r) tiende hacia A y el segundo, tiende hacia infinito. Luego, B tendrá que ser cero

${\displaystyle \begin{array}{l}u(r)=A\sin \left(qr\right)\\ R(r)=A\frac{\sin \left(qr\right)}{r},0\le r\le a\end{array}}$

• La solución de la segunda ecuación diferencial, para r>a, es

${\displaystyle u(r)=C\exp \left(-kr\right)+D\exp \left(kr\right)}$

Cuando r→∞ el segundo término se hace muy grande por lo que D tendrá que ser cero

${\displaystyle \begin{array}{l}u(r)=C\exp \left(-kr\right)\\ R(r)=C\frac{\exp \left(-kr\right)}{r},r>a\end{array}}$

Niveles de energía

En r=a, la solución u(r) o R(r) ha de ser continua y también su derivada primera

${\displaystyle \begin{array}{l}\{\begin{array}{l}A\sin \left(qa\right)=C\exp \left(-ka\right)\\ Aq\cos \left(qa\right)=-Ck\exp \left(-ka\right)\end{array}\\ \tan \left(qa\right)=-\frac{q}{k}\end{array}}$

Como hemos visto, los coeficientes q y k están relacionados

${\displaystyle {\left(qa\right)}^2+{\left(ka\right)}^2=r_0^2,r_0^2=\frac{2m}{{\hslash }^2}{V}_0{a}^2}$

Estas dos últimas ecuaciones determinan los posibles valores de k o los niveles E_n<0 de la energía. Llamamos x=qa, y=ka

${\displaystyle \{\begin{array}{l}y=-\frac{x}{\tan (x)}\\ x^2+y^2=r_0^2\end{array}}$

Representamos circunferencias de radio r₀=π/2, 3π/2, 5π/2, 7π/2 y la función y=-x/tan(x)

hold on
for r0=pi/2:pi:7*pi/2
    fplot(@(x) r0*cos(x), @(x) r0*sin(x),[0,pi/2])
end
for n=0:3
    fplot(@(x) -x./tan(x),[pi/2+n*pi, pi+n*pi])
end
hold off
ylim([0,12])
xlabel('x')
ylabel('y')
grid on
set(gca,'XTick',0:pi/2:4*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi','5\pi/2','3\pi',
'7\pi/2','4\pi'})
title('Niveles de energía')

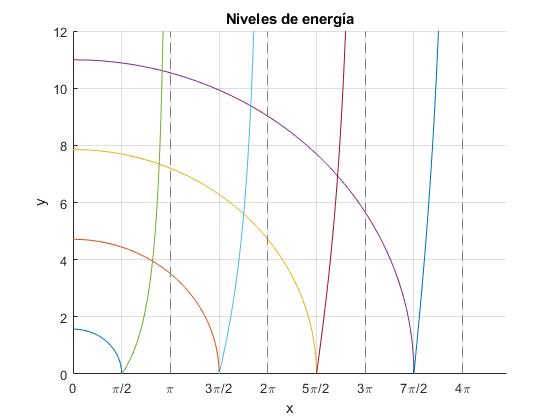
Dado el valor de r₀ o de la energía potencial -V₀. Las ordenadas y=ka de los puntos de intersección, son los posibles valores de k y por tanto, de la energía E

• Para r₀<π/2, no hay puntos de intersección, no hay niveles de energía
• Para π/2<r₀<3π/2, hay un punto de intersección, un nivel de energía
• Para 3π/2<r₀<5π/2, hay dos puntos de intersección, dos niveles de energía
• Para 5π/2<r₀<7π/2, hay tres puntos de intersección, tres niveles de energía
• y así, sucesivamente

La primera ecuación se escribe, alternativamente, ysin(x)+xcos(x)=0

Representamos la función

${\displaystyle f(y)=y\sin \left(\sqrt{r_0^2-y^2}\right)+\sqrt{r_0^2-y^2}\cos \left(\sqrt{r_0^2-y^2}\right)}$

para r₀=π/2, 3π/2, 5π/2, 7π/2. Calculamos las raíces múltiples de la ecuación transcendente f(y)=0, mediante la función raices. Las señalamos mediante puntos de color rojo

function pozo_potencial_1
    hold on
    for r0=pi/2:pi:7*pi/2
        f=@(y) y.*sin(sqrt(r0^2-y.^2))+sqrt(r0^2-y.^2).*cos(sqrt(r0^2-y.^2));
        xx=linspace(0,r0,50);
        rr=raices(f,xx);
        for n=1:length(rr)
            plot(rr(n),0,'ro','markersize',4,'markerfacecolor','r')
        end
        disp(rr)
        fplot(f,[0,r0])
    end
    hold off
    xlabel('y')
    ylabel('f(y)')
    grid on
    title('Raíces')

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

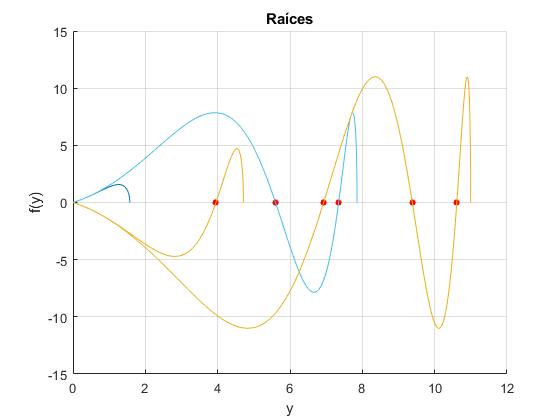
• La primera curva de color azul, r₀=π/2, no tiene raíces
• La segunda curva de color amarillo, r₀=3π/2, tiene una raíz
• La tercera curva de color azul, r₀=5π/2, tiene dos raíces
• La cuarta curva de color amarillo, r₀=7π/2, tiene tres raíces

Función de onda radial R(r)

Una vez que tenemos los niveles de energía E_n o los posibles valores de k para un valor dado de V₀ o r₀, determinamos la parte radial de las funciones de onda

${\displaystyle \begin{array}{l}R(r)=\{\begin{array}{l}A\frac{\sin \left(qr\right)}{r},0\le r\le a\\ C\frac{\exp \left(-kr\right)}{r},r>a\end{array}\\ A\sin \left(qa\right)=C\exp \left(-ka\right)\\ {\left(qa\right)}^2+{\left(ka\right)}^2=r_0^2\end{array}}$

Las dos últimas ecuaciones, relacionan los coeficientes A y C, q y k

El coeficiente A se determina de modo que la integral

${\displaystyle {\displaystyle \underset{0}{\overset{a}{\int }}{A}^2\frac{{\sin }^2\left(qr\right)}{r^2}{r}^{2}dr}+{\displaystyle \underset{a}{\overset{\infty }{\int }}{C}^2\frac{\exp \left(-2kr\right)}{r^2}{r}^{2}dr=1}}$

El resultado es

${\displaystyle \begin{array}{l}{A}^2\left\{{\displaystyle \underset{0}{\overset{a}{\int }}{\sin }^2\left(qr\right)dr+\frac{{\sin }^2\left(qa\right)}{\exp \left(-2ka\right)}{\displaystyle \underset{a}{\overset{\infty }{\int }}\exp \left(-2kr\right)dr}}\right\}=1\\ A^2\left\{\frac{1}{2}\left(a-\frac{\sin \left(2qa\right)}{2q}\right)+\frac{{\sin }^2\left(qa\right)}{2k}\right\}=1\end{array}}$

Representamos las funciones de onda correspondientes a los tres niveles de energía para r₀=7π/2. El nivel más bajo de energía (estado fundamental) es el valor más grande de k=10.6126

function pozo_potencial_2
    a=1;
    r0=7*pi/2;
    f=@(y) y.*sin(sqrt(r0^2-y.^2))+sqrt(r0^2-y.^2).*cos(sqrt(r0^2-y.^2));
    xx=linspace(0,r0,50);
    rr=raices(f,xx);
    disp(rr)
    hold on
    for k=rr
        q=sqrt(r0^2-k^2);
        A=1/sqrt((a/2-sin(2*q*a)/(4*q)+sin(q*a)^2/(2*k)));
        C=A*sin(q*a)/exp(-k*a);
        R=@(r) (A*(r<=a).*sin(q*r))./r+(C*(r>a).*exp(-k*r))./r;
        fplot(R,[0,2*a])
    end
    hold off
    xlabel('r')
    legend('2','1','fundamental','Location', 'best')
    ylabel('R(r)')
    grid on
    title('Función de onda, l=0')

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

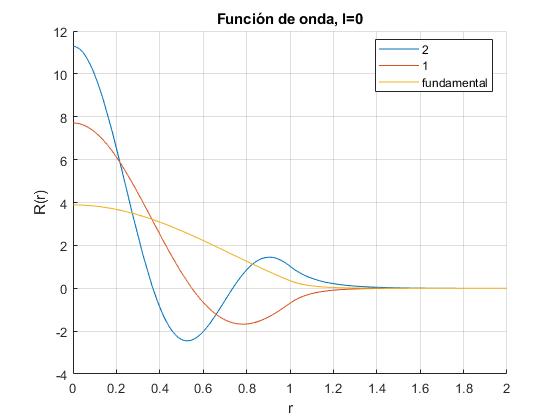
Los posibles valores de ka son

6.9311    9.3818   10.6126

Solución general, l≠0

• Solución de la primera ecuación diferencial, para r≤a

${\displaystyle \frac{d^{2}u}{d{r}^2}+\left\{q^2-\frac{l(l+1)}{r^2}\right\}u=\mathrm{0,}{q}^2=\frac{2m}{{\hslash }^2}\left(E+V_0\right),0\le r\le a}$

La solución de esta ecuación diferencial ya se ha estudiado en la página titulada La ecuación de Schrödinger en coordenadas esféricas. (Véase en la página titulada Funciones de Bessel el apartado, Funciones esféricas de Bessel)

${\displaystyle $ u(r)=Ar·j_l(qr)+Br·y_l(qr)$}$

Ahora bien, y_l(kr)→∞ cuando r→0, el coeficiente B tendrá que ser cero. La solución es

${\displaystyle R(r)=\frac{u(r)}{r}=A{j}_l\left(qr\right)}$

• Solución de la segunda ecuación diferencial, para r>a

${\displaystyle \frac{d^{2}u}{d{r}^2}+\left\{-k^2-\frac{l(l+1)}{r^2}\right\}u=\mathrm{0,}r>a}$

Llamando ρ=ikr, donde i es la unidad imaginaria. La ecuación diferencial se transforma

${\displaystyle \begin{array}{l}\frac{d^{2}u}{d{\rho }^2}+\left(1-\frac{l(l+1)}{{\rho }^2}\right)u=0\\ {\rho }^2\frac{d^{2}u}{d{\rho }^2}+\left({\rho }^2-l(l+1)\right)u=0\end{array}}$

La solución de esta ecuación diferencial ya se ha estudiado en la página titulada La ecuación de Schrödinger en coordenadas esféricas. (Véase en la página titulada Funciones de Bessel el apartado, Funciones esféricas de Bessel)

${\displaystyle \begin{array}{l}u(\rho )=C\rho ·j_l(\rho )+D\rho ·y_l(\rho )\\ u(r)=C·ikr·j_l\left(ikr\right)+D·ikr·y_l\left(ikr\right)\\ R(r)=\frac{u(r)}{r}=C·h_l^{(1)}\left(ikr\right)+D·h_l^{(2)}\left(ikr\right)\end{array}}$

La solución es una combinación de las funciones esféricas de Hankel. La segunda diverge cuando r→∞, por lo que el coeficiente D tendrá que ser nulo. La solución de la ecuación diferencial es

${\displaystyle R(r)=C·h_l^{(1)}\left(ikr\right)}$

Niveles de energía

La componente radial R(r) de la función de onda ha de ser continua y también su derivada primera en r=a

${\displaystyle \{\begin{array}{l}A{j}_l\left(qa\right)=C{h}_l^{(1)}\left(ika\right)\\ A{\frac{d{j}_l\left(qr\right)}{dr}|}_{r=a}=C{\frac{d{h}_l^{(1)}\left(ikr\right)}{dr}|}_{r=a}\end{array}}$

Teniendo en cuenta las propiedades de estas funciones

${\displaystyle \begin{array}{l}\frac{d{j}_l(z)}{dz}=j_{l-1}(z)-\frac{l+1}{z}{j}_l(z)\\ \frac{d{h}_l^{(1)}(z)}{dz}=h_{l-1}^{(1)}(z)-\frac{l+1}{z}{h}_l^{(1)}(z)\end{array}}$

El sistema de dos ecuaciones se convierte en una ecuación transcendente

${\displaystyle \begin{array}{l}\{\begin{array}{l}A{j}_l\left(qa\right)=C{h}_l^{(1)}\left(ika\right)\\ A{k}_0\left\{j_{l-1}\left(qa\right)-\frac{l+1}{k_{0}a}{j}_l\left(qa\right)\right\}=Cik\left\{h_{l-1}^{(1)}\left(ika\right)-\frac{l+1}{ika}{h}_l^{(1)}\left(ika\right)\right\}\end{array}\\ \frac{k_0\left(j_{l-1}\left(qa\right)-\frac{l+1}{k_{0}a}{j}_l\left(qa\right)\right)}{j_l\left(qa\right)}=\frac{ik\left(h_{l-1}^{(1)}\left(ika\right)-\frac{l+1}{ika}{h}_l^{(1)}\left(ika\right)\right)}{h_l^{(1)}\left(ika\right)}\\ q·j_{l-1}\left(qa\right)h_l^{(1)}\left(ika\right)-ik{h}_{l-1}^{(1)}\left(ika\right)j_l\left(qa\right)=0\end{array}}$

Los coeficientes q y k están relacionados

${\displaystyle {\left(qa\right)}^2+{\left(ka\right)}^2=r_0^2}$

Calculamos los ceros de la ecuación transcendente en k

${\displaystyle f(k)=\sqrt{r_0^2/a^2-k^2}·j_{l-1}\left(\sqrt{r_0^2-k^2{a}^2}\right)h_l^{(1)}\left(ika\right)-ik{h}_{l-1}^{(1)}\left(ika\right)j_l\left(\sqrt{r_0^2-k^2{a}^2}\right)}$

La función f(k) es real para l par e imaginaria para l impar. Para calcular los ceros la función f(k) tiene que ser real por lo que se multiplica por i^l. El signo de la función carece de importancia

En la página titulada Funciones de Bessel el apartado, Funciones esféricas de Bessel), proporcionamos las expresiones de las primeras funciones esféricas de Bessel j_l(x) y de Hankel. Vamos a trabajar con estas funciones antes de utilizar las propias de MATLAB

Establecemos el valor de r₀=7π/2. Comprobamos que para l=0, obtenemos las mismos valores de k

function pozo_potencial_6
   j_1=@(x) cos(x)./x;
   j0=@(x) sin(x)./x;
   j1=@(x) (sin(x)-x.*cos(x))./(x.^2);
   j2=@(x) ((3-x.^2).*sin(x)-3*x.*cos(x))./x.^3;
   j3=@(x) (3*(5-2*x.^2).*sin(x)-x.*(15-x.^2).*cos(x))./x.^4;
   Jfunc={j_1,j0,j1,j2,j3};
   
   h_1=@(x) exp(1i*x)./x;
   h0=@(x) -1i*exp(1i*x)./x;
   h1=@(x) -((x+1i).*exp(1i*x))./(x.^2);
   h2=@(x) (1i*(x.^2+3*1i*x-3).*exp(1i*x))./x.^3;    
   h3=@(x) ((x.^3+6*1i*x.^2-15*x-15*1i).*exp(1i*x))./x.^4;
   Hfunc={h_1,h0,h1,h2,h3};
      
    l=0; %cambiar a 1,2, 3 como máximo
    a=1;
    r0=7*pi/2;
 
    q=@(y) sqrt(r0^2-y.^2);
    f=@(y) ((q(y).*Jfunc{l+1}(q(y)*a)).*Hfunc{l+2}(1i*y*a)-
1i*(y.*Hfunc{l+1}(1i*y*a)).*Jfunc{l+2}(q(y)*a))*(1i)^l;
    xx=linspace(0,r0,50);
    rr=raices(f,xx);
    disp(rr)

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

6.9311    9.3818   10.6126

Calculamos los niveles de energía E_n o los posibles valores de k dado r₀ o V₀. Para los valores l=0, 1, 2, 3

Los mismos resultados se obtienen utilizando las funciones besselj, besselh de MATLAB. Hay que tener en cuenta que las funciones esféricas se definen

${\displaystyle j_l(x)=\sqrt{\frac{\pi }{2x}}{J}_{l+\frac{1}{2}}(x),h_l^{(1)}(x)=\sqrt{\frac{\pi }{2x}}{H}_{l+\frac{1}{2}}^{(1)}(x)}$

function pozo_potencial_4
    l=0; %cambiar a 1,2,3...
    a=1;
    r0=7*pi/2;
    %funciones esféricas de Bessel
    q=@(y) sqrt(r0^2-y.^2);
    h0=@(y) sqrt(pi./(2*y)).*besselh(l+1/2,1,y);
    h1=@(y) sqrt(pi./(2*y)).*besselh(l-1/2,1,y);
    j0=@(y) sqrt(pi./(2*y)).*besselj(l+1/2,y);
    j1=@(y) sqrt(pi./(2*y)).*besselj(l-1/2,y);
    
    f=@(y) ((q(y).*j1(q(y))).*h0(1i*y)-(1i*y.*h1(1i*y)).*j0(q(y)))*(1i)^l;
    xx=linspace(0,r0,50);
    rr=raices(f,xx);
    disp(rr)

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

Función de onda radial R(r)

Una vez que tenemos los niveles de energía E_n o los posibles valores de k para un valor dado de V₀ o r₀. Determinamos la parte radial de la función de onda

${\displaystyle \begin{array}{l}R(r)=\{\begin{array}{l}A{j}_l\left(k_{0}r\right),0\le r\le a\\ C{h}_l^{(1)}\left(ikr\right),r>a\end{array}\\ A{j}_l\left(qa\right)=C{h}_l^{(1)}\left(ika\right)\\ {\left(qa\right)}^2+{\left(ka\right)}^2=r_0^2\end{array}}$

Las dos últimas ecuaciones, relacionan los coeficientes A y C, q y k

El coeficiente A se determina de modo que la integral

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{a}{\int }}{\left(A{j}_l\left(qr\right)\right)}^2{r}^{2}dr}+{\displaystyle \underset{a}{\overset{\infty }{\int }}{\left(C{h}_l^{(1)}\left(ikr\right)\right)}^2{r}^{2}dr=1}\\ A^2\left\{{\displaystyle \underset{0}{\overset{a}{\int }}{\left(r·j_l\left(qr\right)\right)}^{2}dr+{\left(\frac{j_l\left(qa\right)}{h_l^{(1)}\left(ika\right)}\right)}^2{\displaystyle \underset{a}{\overset{\infty }{\int }}{\left(r·h_l^{(1)}\left(ikr\right)\right)}^{2}dr}}\right\}=1\end{array}}$

Representamos las funciones de onda correspondientes a los tres niveles de energía para r₀=7π/2 y para l=0. Comprobamos que obtenemos la misma representación gráfica que en el apartado anterior. Cambiamos a l=1.

function pozo_potencial_5
    l=1;
    a=1;
    r0=7*pi/2;
    %funciones esféricas de Bessel
    q=@(y) sqrt(r0^2-y.^2);
    h0=@(y) sqrt(pi./(2*y)).*besselh(l+1/2,1,y);
    h1=@(y) sqrt(pi./(2*y)).*besselh(l-1/2,1,y);
    j0=@(y) sqrt(pi./(2*y)).*besselj(l+1/2,y);
    j1=@(y) sqrt(pi./(2*y)).*besselj(l-1/2,y);
    f=@(y) ((q(y).*j1(q(y))).*h0(1i*y)-(1i*y.*h1(1i*y)).*j0(q(y)))*(1i)^l;
    xx=linspace(0,r0,50);
    rr=raices(f,xx);
    disp(rr)
    hold on
    for k=rr
        q=sqrt(r0^2-k^2);
        C=j0(q*a)/h0(1i*k*a);
        f_1=@(x) (x.*j0(q*x)).^2;
        f_2=@(x) (x.*h0(1i*k*x)).^2;
        A=1/sqrt(integral(f_1,0,a)+C^2*integral(f_2,a,10*a));
        C=C*A;
        R=@(r) A*(r<=a).*j0(q*r)+C*(r>a).*h0(1i*k*r);
        fplot(R,[0,2*a])
    end
    hold off
    xlabel('r')
    ylabel('R(r)')
    legend('2','1','fundamental','Location', 'best')
    grid on
    title('Función de onda, l=1')

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

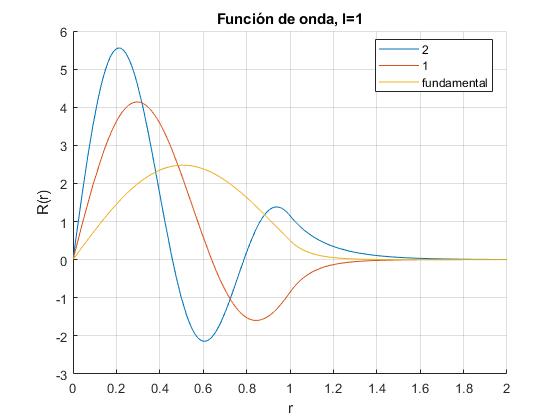
El nivel más bajo de energía (estado fundamental) es el valor más grande de k=10.1981

4.9686    8.4518   10.1981

Referencias

Masatsugu Sei Suzuki, Itsuko S. Suzuki. Finite spherical square well potential: deuteron, with the use of Mathematica https://www.researchgate.net/publication/348819348_Finite_spherical_square_ well_potential_deuteron_with_the_use_of_Mathematica