Representamos el potencial delta de Dirac por la función que se muestra en la figura, un pozo centrado en a de anchura 2ε y profundidad que tiende a infinito, siendo ε→0.

${\displaystyle V(x)=-\alpha \frac{{\hslash }^2}{2m}\delta (x-a)}$

En el origen, representamos una barrera de potencial de altura y profundidad infinita

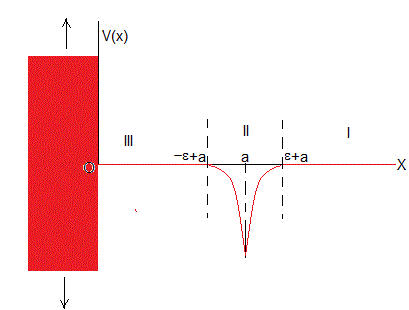
Energía E<0

Vamos a estudiar el efecto de la barrera de potencial sobre el único nivel de energía del pozo de potencial delta de Dirac

En este apartado, resolveremos la ecuación de Schrödinger para el pozo de potencial delta de Dirac centrado en la posición x=a

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}\frac{{\partial }^2\psi (x)}{\partial x^2}+V(x)·\psi (x)=E·\psi (x)\\ -\frac{{\hslash }^2}{2m}\frac{{\partial }^2\psi (x)}{\partial x^2}-\alpha \frac{{\hslash }^2}{2m}\delta (x-a)·\psi (x)=E·\psi (x)\end{array}}$

Vamos a considerar tres regiones

${\displaystyle \{\begin{array}{l}x>\epsilon +a,V(x)=0\\ -\epsilon +a<x<\epsilon +a,V(x)=-\alpha \frac{{\hslash }^2}{2m}\delta (x-a)\\ 0<x<-\epsilon +a,V(x)=0\\ x\ge \mathrm{0,}V(x)=\infty \end{array}}$

donde ε→0 es muy pequeño

• Región I, x>ε+a

${\displaystyle \begin{array}{l}\frac{{\partial }^2\psi }{\partial x^2}+\frac{2m}{{\hslash }^2}E·\psi =\mathrm{0,}E<0\\ \frac{{\partial }^2\psi }{\partial x^2}-k^2·\psi =\mathrm{0,}{k}^2=-\frac{2m}{{\hslash }^2}E\\ {\psi }_I(x)=A\exp (-kx)+B\exp (kx)\end{array}}$

Cuando x se hace grande el segundo término tiende hacia infinito, por lo que el coeficiente B deberá ser cero

${\displaystyle {\psi }_I(x)=A\exp (-kx),x>\epsilon +a}$

• Región III, 0<x<-ε+a

${\displaystyle \begin{array}{l}\frac{{\partial }^2\psi }{\partial x^2}-k^2·\psi =\mathrm{0,}{k}^2=-\frac{2m}{{\hslash }^2}E\\ {\psi }_{III}(x)=C\exp (-kx)+D\exp (kx),0<x<-\epsilon +a\end{array}}$

Nivel de energia (si existe)

• En x=0, se anula la función de onda

${\displaystyle \begin{array}{l}{\psi }_{III}(0)=0\\ C+D=0\\ {\psi }_{III}(x)=D\left(\exp (kx)-\exp (-kx)\right)=2D\sinh (kx),0<x<-\epsilon +a\end{array}}$

• La función de onda deberá ser continua en x=a.

Como la región II tiene una achura 2ε, infinitamente pequeña, la continuidad de la función de onda

${\displaystyle \begin{array}{l}{\psi }_I(a)={\psi }_{III}(a)\\ A\exp (-ka)=2D\sinh (ka)\\ D=A\frac{\exp (-ka)}{2\sinh (ka)}\end{array}}$

La función de onda en las regiones I y III es

${\displaystyle \{\begin{array}{l}{\psi }_I(x)=A\exp (-kx),x>a\\ {\psi }_{III}(x)=A\frac{\exp (-ka)}{\sinh (ka)}\sinh (kx),x<a\end{array}}$

• La segunda condición, de que la derivada primera sea continua, no se cumple en este caso. Integramos la ecuación de Schrödinger en el pequeño intervalo de (a-ε, a+ε)

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}{\displaystyle \underset{a-\epsilon }{\overset{a+\epsilon }{\int }}\frac{{\partial }^2\psi (x)}{\partial x^2}}dx-{\displaystyle \underset{a-\epsilon }{\overset{a-\epsilon }{\int }}\alpha \frac{{\hslash }^2}{2m}\delta (x-a)·\psi (x)·dx}=E·{\displaystyle \underset{a-\epsilon }{\overset{a+\epsilon }{\int }}\psi (x)·dx}\\ -\frac{{\hslash }^2}{2m}\underset{\epsilon \to 0}{\lim }\left({\frac{\partial {\psi }_I(x)}{\partial x}|}_{a+\epsilon }-{\frac{\partial {\psi }_{III}(x)}{\partial x}|}_{a-\epsilon }\right)-\alpha \frac{{\hslash }^2}{2m}\psi (a)=0\\ \underset{\epsilon \to 0}{\lim }\left({-kA\exp \left(-kx\right)|}_{a+\epsilon }-{kA\frac{\exp (-ka)}{\sinh (ka)}\cosh \left(kx\right)|}_{a-\epsilon }\right)=-\alpha A\exp \left(-ka\right)\\ \underset{\epsilon \to 0}{\lim }\left(-kA\exp \left(-k\left(a+\epsilon \right)\right)-kA\frac{\exp (-ka)}{\sinh (ka)}\cosh \left(k\left(a-\epsilon \right)\right)|\right)=-\alpha A\exp \left(-ka\right)\\ -k\exp \left(-ka\right)-k\frac{\exp (-ka)}{\sinh (ka)}\cosh \left(ka\right)=-\alpha \exp \left(-ka\right)\\ \tanh \left(ka\right)=\frac{k}{\alpha -k}\\ \frac{1-\exp \left(-2ka\right)}{1+\exp \left(-2ka\right)}=\frac{k}{\alpha -k}\\ 1-2\frac{k}{\alpha }=\exp \left(-2ka\right)\end{array}}$

Una raíz es k=0. La raíz buscada, si existe, se obtiene resolviendo la ecuación transcendente utilizando la función fzero de MATLAB

Representamos la recta y=1-2k/α y la función y=exp(-2ka). Vemos que se cortan en el origen y en otro punto

alfa=1;
a=2;
f=@(k) exp(-2*k*a);
g=@(k) 1-2*k/alfa;
h=@(k) g(k)-f(k);
r1=fzero(h,alfa/2);
hold on
fplot(f,[0, 1])
fplot(g,[0, 1])
line([r1,r1],[-0.2,f(r1)],'lineStyle','--')
hold off
grid on
ylim([-0.2,1.1])
xlabel('k')
ylabel('f(k)')
title('Raíz de la ecuación transcedente')
disp(r1)



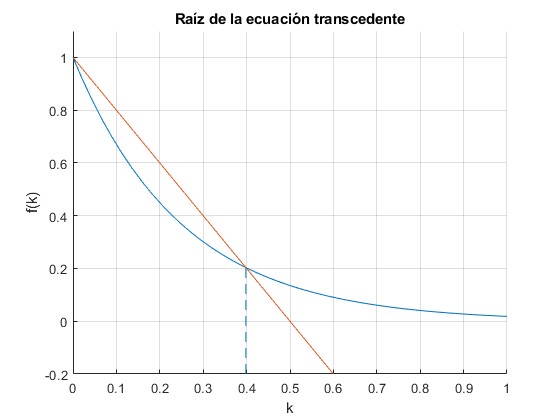
La raíz buscada es k=0.3984

 0.3984 

La energía del nivel es negativa

${\displaystyle E=-\frac{{\hslash }^2{k}^2}{2m}}$

La recta y la función exponencial se cortan, siempre que la pendiente en el origen de la recta -2/α sea mayor que la pendiente de dicha función

${\displaystyle \begin{array}{l}-\frac{2}{\alpha }>{\left(\frac{d}{dk}\exp \left(-2ka\right)\right)}_{k=0}\\ -\frac{2}{\alpha }>-2a\\ \frac{1}{\alpha }>a\\ a\alpha <1\end{array}}$

Para comprobarlo, cambiamos la primera línea del código alfa=0.3;



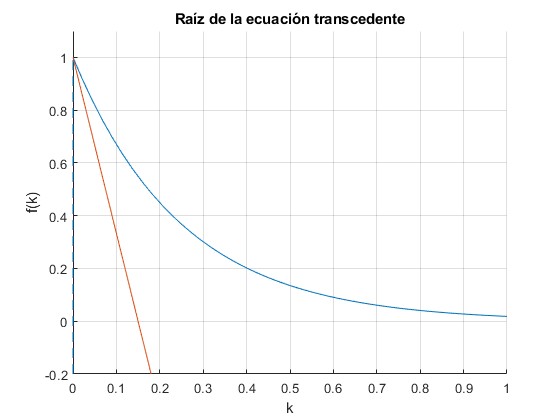
Cuando a es grande, exp(-2ka)→0

${\displaystyle \begin{array}{l}1-2\frac{k}{\alpha }\to 0\\ k\to \frac{\alpha }{2}\end{array}}$

Resultado que ya hemos obtenido, cuando calculamos el nivel de energía de un potencial delta de Dirac

${\displaystyle E=-\frac{{\hslash }^2{\alpha }^2}{8m}}$

La energía del nivel se modifica. Cuando no hay barrera para α=1, el valor k=0.5. La presencia de la barrera modifica el valor de k=0.3984 (y por tanto, de la energía del nivel) cuando la distancia entre la barrera y el pozo de potencial es a=2

Función de onda

La función de onda en las regiones I y III

${\displaystyle \{\begin{array}{l}{\psi }_I(x)=A\exp (-kx),x>a\\ {\psi }_{III}(x)=A\frac{\exp (-ka)}{\sinh (ka)}\sinh (kx),x<a\end{array}}$

El coeficiente A se calcula de modo que

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{a}{\int }}{\left(A\frac{\exp (-ka)}{\sinh (ka)}\sinh (kx)\right)}^{2}dx+}{\displaystyle \underset{a}{\overset{\infty }{\int }}{\left(A\exp (-kx)\right)}^{2}dx}=1\\ A^2{\left(\frac{\exp (-ka)}{\sinh (ka)}\right)}^2{\displaystyle \underset{0}{\overset{a}{\int }}{\sinh }^2(kx)dx+A^2}{\displaystyle \underset{a}{\overset{\infty }{\int }}\exp \left(-2kx\right)dx}=1\\ A^2{\left(\frac{\exp (-ka)}{\sinh (ka)}\right)}^2{\displaystyle \underset{0}{\overset{a}{\int }}\frac{\cosh \left(2kx\right)-1}{2}dx+A^2\frac{-1}{2k}}\left(0-\exp \left(-2ka\right)\right)=1\\ A^2{\left(\frac{\exp (-ka)}{\sinh (ka)}\right)}^2\frac{1}{2}\left(\frac{\sinh \left(2ka\right)}{2k}-a\right)+A^2\frac{\exp \left(-2ka\right)}{2k}=1\\ \frac{1}{2}{A}^2\left\{\exp (-2ka)\frac{\cosh \left(ka\right)}{k\sinh (ka)}-a{\left(\frac{\exp (-ka)}{\sinh (ka)}\right)}^2+\frac{\exp \left(-2ka\right)}{k}\right\}=1\\ A^2\left\{\frac{\exp \left(-2ka\right)}{k}\left(\coth \left(ka\right)+1\right)-a{\left(\frac{\exp (-ka)}{\sinh (ka)}\right)}^2\right\}=2\end{array}}$

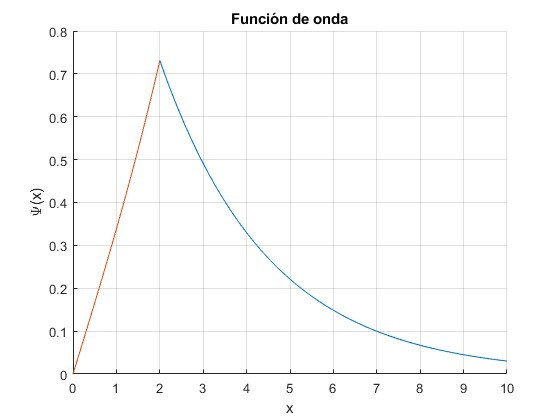
Representamos la función de onda correspondiente al nivel de energía k=0.3984, es decir, con α=1, a=2

alfa=1;
a=2;
f=@(x) x./(alfa-x);
g=@(x) tanh(x*a);
h=@(x) g(x)-f(x);
r1=fzero(h,alfa/2);
disp(r1)
k=r1;
A=sqrt(2/(exp(-2*k*a)*(coth(k*a)+1)/k-a*exp(-2*k*a)/sinh(k*a)^2));
D=A*exp(-k*a)/(2*sinh(k*a));
f=@(x) A*exp(-k*x);
g=@(x) 2*D*sinh(k*x);
hold on
fplot(f,[a,10])
fplot(g,[0,a])
hold off
grid on
xlabel('x')
ylabel('\Psi(x)')
title('Función de onda')

 0.3984 

La función de onda es continua en x=a pero no lo es su derivada primera

Energía E>0

• Región I, x>a+ε

${\displaystyle \begin{array}{l}\frac{{\partial }^2\psi }{\partial x^2}+\frac{2m}{{\hslash }^2}E·\psi =\mathrm{0,}E>0\\ \frac{{\partial }^2\psi }{\partial x^2}+k^2·\psi =\mathrm{0,}{k}^2=\frac{2m}{{\hslash }^2}E\\ {\psi }_I(x)=A\exp (-ikx)+B\exp (ikx)\end{array}}$

• Región III, 0<x<a-ε

${\displaystyle \begin{array}{l}\frac{{\partial }^2\psi }{\partial x^2}+k^2·\psi =\mathrm{0,}{k}^2=\frac{2m}{{\hslash }^2}E\\ {\psi }_{III}(x)=C\exp (-ikx)+D\exp (ikx)\end{array}}$

Relaciones entre los coeficientes

• En x=0, se anula la función de onda

${\displaystyle \begin{array}{l}{\psi }_{III}(0)=0\\ C+D=0\\ {\psi }_{III}(x)=D\left(\exp (kx)-\exp (-kx)\right)=2D\sinh (kx),0<x<-\epsilon +a\end{array}}$

• La función de onda deberá ser continua en x=a.

Como la región II tiene una achura 2ε, infinitamente pequeña, la continuidad de la función de onda

${\displaystyle \begin{array}{l}{\psi }_I(a)={\psi }_{III}(a)\\ A\exp (-ika)+B\exp (ika)=2iD\sin (ka)\\ D=\frac{A\exp (-ika)+B\exp (ika)}{2i\sin (ka)}\end{array}}$

La función de onda en las regiones I y III es

${\displaystyle \{\begin{array}{l}{\psi }_I(x)=A\exp (-ikx)+B\exp (ikx),x>a\\ {\psi }_{III}(x)=2iD\sin (kx),x<a\end{array}}$

• La segunda condición, de que la derivada primera sea continua, no se cumple en este caso. Integramos la ecuación de Schrödinger en el pequeño intervalo de (a-ε, a+ε)

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}\underset{\epsilon \to 0}{\lim }\left({\frac{\partial {\psi }_I(x)}{\partial x}|}_{a+\epsilon }-{\frac{\partial {\psi }_{III}(x)}{\partial x}|}_{a-\epsilon }\right)-\alpha \frac{{\hslash }^2}{2m}\psi (a)=0\\ \underset{\epsilon \to 0}{\lim }\left({ik\left(-A\exp \left(-ikx\right)+B\exp \left(ikx\right)\right)|}_{a+\epsilon }-{2ikD\cos \left(kx\right)|}_{a-\epsilon }\right)=-\alpha 2iD\sin \left(ka\right)\\ ik\underset{\epsilon \to 0}{\lim }\left(-A\exp \left(-ik\left(a+\epsilon \right)\right)+B\exp \left(ik\left(a+\epsilon \right)\right)-2D\cos \left(k\left(a-\epsilon \right)\right)\right)=-2i\alpha D\sin \left(ka\right)\\ ik\underset{\epsilon \to 0}{\lim }\left(-A\exp \left(-ik\left(a+\epsilon \right)\right)+B\exp \left(ik\left(a+\epsilon \right)\right)-2D\cos \left(k\left(a-\epsilon \right)\right)\right)=-2i\alpha D\sin \left(ka\right)\\ ik\left(-A\exp \left(-ika\right)+B\exp \left(ika\right)-2D\cos \left(ka\right)\right)=-2i\alpha D\sin \left(ka\right)\\ ik\left(-A\exp \left(-ika\right)+B\exp \left(ika\right)\right)=2iD\left(k\cos \left(ka\right)-\alpha \sin \left(ka\right)\right)\\ ik\left(-A\exp \left(-ika\right)+B\exp \left(ika\right)\right)=2i\frac{A\exp (-ika)+B\exp (ika)}{2i\sin (ka)}\left(k\cos \left(ka\right)-\alpha \sin \left(ka\right)\right)\\ ik\left(-A\exp \left(-ika\right)+B\exp \left(ika\right)\right)=\left(A\exp (-ika)+B\exp (ika)\right)\left(\frac{k\cos \left(ka\right)}{\sin (ka)}-\alpha \right)\\ A\exp \left(-ika\right)\left(-ik-\frac{k\cos \left(ka\right)}{\sin (ka)}+\alpha \right)+B\exp \left(ika\right)\left(ik-\frac{k\cos \left(ka\right)}{\sin (ka)}+\alpha \right)=0\\ B=A\exp \left(-2ika\right)\frac{k\cos \left(ka\right)-\alpha \sin (ka)+ik\sin (ka)}{-k\cos \left(ka\right)+\alpha \sin (ka)+ik\sin (ka)}\end{array}}$

Comprobamos que ${\left|B\right|}^2={\left|A\right|}^2$. Todas las partículas incidentes se reflejan en la barrera de potencial

Conocido B se calcula D

${\displaystyle \begin{array}{l}D=\frac{A\exp (-ika)+A\exp \left(-2ika\right)\frac{k\cos \left(ka\right)-\alpha \sin (ka)+ik\sin (ka)}{-k\cos \left(ka\right)+\alpha \sin (ka)+ik\sin (ka)}\exp (ika)}{2i\sin (ka)}=\\ D=A\frac{k\exp \left(-ika\right)}{-k\cos \left(ka\right)+\alpha \sin (ka)+ik\sin (ka)}\end{array}}$

Función de onda

Representamos la función de onda para α=1, a=2, con k=3

alfa=1;
a=2;
k=3;
B=exp(-1i*2*k*a)*(k*cos(k*a)-alfa*sin(k*a)+1i*k*sin(k*a))/
(-k*cos(k*a)+alfa*sin(k*a)+1i*k*sin(k*a));
D=k*exp(-1i*k*a)/(-k*cos(k*a)+alfa*sin(k*a)+1i*k*sin(k*a));
f=@(x) real(exp(-1i*k*x)+B*exp(1i*k*x));
g=@(x) real(2*1i*D*sin(k*x));
hold on
fplot(f,[a, 7])
fplot(g,[0, a])
hold off
grid on
xlabel('x')
ylabel('\Psi(x)')
title('Función de onda')

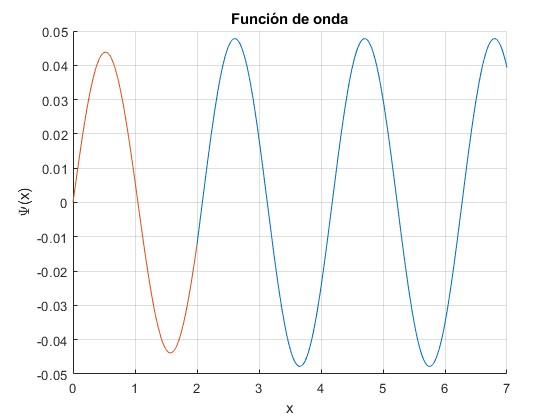
Otra forma alternativa de representar la función de onda. Desfase

Los módulos de los coeficientes complejos A y B son iguales. En forma compleja

${\displaystyle \begin{array}{l}A=\left|A\right|\exp \left(i\phi \right)\\ B=\left|A\right|\exp \left(i\theta \right)\\ \{\begin{array}{l}{\psi }_I(x)=\left|A\right|\left(\exp \left(i\left(-kx+\phi \right)\right)+\exp \left(i\left(kx+\theta \right)\right)\right),x>a\\ {\psi }_{III}(x)=2D\sin (kx),x<a\end{array}\end{array}}$

Para que la suma de exponenciales sea real, se tiene que cumplir que φ=-θ

${\displaystyle {\psi }_I(x)=\left|A\right|\left(\exp \left(i\left(-kx-\theta \right)\right)+\exp \left(i\left(kx+\theta \right)\right)\right)=2\left|A\right|\cos \left(kx+\theta \right)}$

• La función de onda deberá ser continua en x=a.

${\displaystyle 2\left|A\right|\cos \left(ka+\theta \right)=2D\sin (ka)}$

• La segunda condición, de que la derivada primera sea continua, no se cumple en este caso. Integramos la ecuación de Schrödinger en el pequeño intervalo de (a-ε, a+ε)

${\displaystyle \begin{array}{l}\underset{\epsilon \to 0}{\lim }\left({\frac{\partial {\psi }_I(x)}{\partial x}|}_{a+\epsilon }-{\frac{\partial {\psi }_{III}(x)}{\partial x}|}_{a-\epsilon }\right)+\alpha \psi (a)=0\\ \underset{\epsilon \to 0}{\lim }\left(-2k\left|A\right|\sin \left(k(a+\epsilon )+\theta \right)-2kD\cos \left(k(a-\epsilon \right)\right)+2\alpha D\sin \left(ka\right)=0\\ k\left|A\right|\sin \left(ka+\theta \right)+kD\cos \left(ka\right)=\alpha D\sin \left(ka\right)\end{array}}$

Resolvemos el sistema de ecuaciones

${\displaystyle \begin{array}{l}\{\begin{array}{l}\left|A\right|\cos \left(ka+\theta \right)=D\sin (ka)\\ k\left|A\right|\sin \left(ka+\theta \right)=D\left(\alpha \sin \left(ka\right)-k\cos \left(ka\right)\right)\end{array}\\ k\tan \left(ka+\theta \right)=\frac{\alpha \sin \left(ka\right)-k\cos \left(ka\right)}{\sin (ka)}\end{array}}$

Despejamos θ y D

${\displaystyle \begin{array}{l}\tan \theta =\frac{\alpha \sin \left(ka\right)\cos \left(ka\right)-k}{\alpha {\sin }^2\left(ka\right)}\\ D=\left|A\right|\frac{\cos \left(ka+\theta \right)}{\sin (ka)}\end{array}}$

Representamos el ángulo de desfase θ en función de ka/π manteniendo fijo a=2 y para dos valores del parámetro α, 0.5/a y 30/a

a=2;
hold on
alfa=0.5/a;
th=@(x) atan((alfa*sin(pi*x).*cos(pi*x)-pi*x/a)./(alfa*sin(pi*x).^2));
fplot(th,[0,5])
alfa=30/a;
th=@(x) atan((alfa*sin(pi*x).*cos(pi*x)-pi*x/a)./(alfa*sin(pi*x).^2));
fplot(th,[0,5])
hold off
grid on
xlabel('k*a/\pi')
legend('0.5/a','30/a','location','best')
set(gca,'YTick',-pi/2:pi/6:2*pi)
set(gca,'YTickLabel',{'-\pi/2','-\pi/3','-\pi/6','0','\pi/6','\pi/3','\pi/2'})
ylabel('\theta')
title('Desfase')

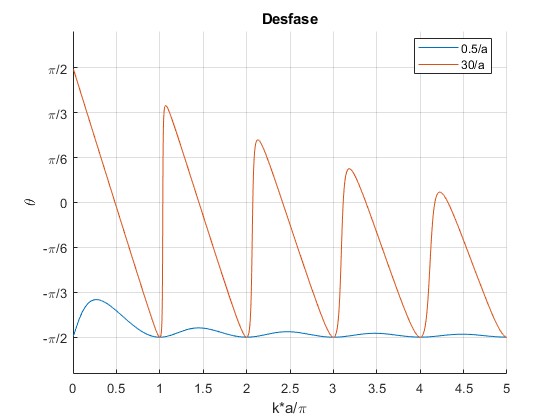
Los mínimos del desfase coinciden con valores enteros de ka/π

Representamos la función de onda para α=1, a=2, con k=3

alfa=1;
a=2;
k=3;
th=atan((alfa*sin(k*a)*cos(k*a)-k)/(alfa*sin(k*a)^2)); %desfase
D=cos(k*a+th)/sin(k*a);
f=@(x) cos(k*x+th);
g=@(x) D*sin(k*x);
hold on
fplot(f,[a, 7])
fplot(g,[0, a])
hold off
grid on
xlabel('x')
ylabel('\Psi(x)')
title('Función de onda')

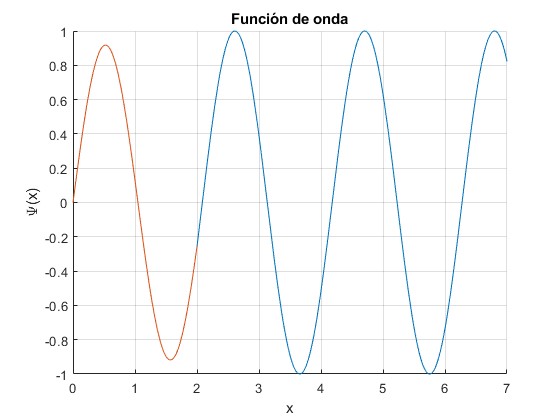
Las representación gráfica coincide excepto en la escala vertical

Referencias

Claude Aslangul. δ well with a reflecting barrier. Am. J. Phys. 63 (10) October 1995, pp. 935-940