Potencial mgx

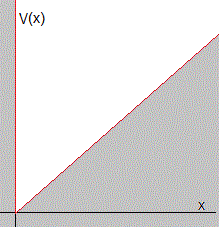
Estudiamos los niveles de energía y las funciones de onda de una partícula de masa m que se mueve en un potencial V(x):

• pared infinita en x=0
• mgx para x>0

La ecuación de Schrödinger para x>0

${\displaystyle \frac{-{\hslash }^2}{2m}\frac{d^2\Psi (x)}{d{x}^2}+mgx=E\Psi (x)}$

Hacemos la sustitución x'=αmgx y E'=αE

${\displaystyle \begin{array}{l}\frac{{\hslash }^2}{2m}{\alpha }^2{m}^2{g}^2\frac{d^2\Psi }{dx{\text{'}}^2}-\frac{x\text{'}-E\text{'}}{\alpha }\Psi =0\\ \frac{m{g}^2{\hslash }^2}{2}{\alpha }^3\frac{d^2\Psi }{dx{\text{'}}^2}-\left(x\text{'}-E\text{'}\right)\Psi =0\end{array}}$

Tomando

${\displaystyle \alpha ={\left(\frac{2}{{\hslash }^{2}m{g}^2}\right)}^{1/3}}$

Nos queda la ecuación diferencial

${\displaystyle \frac{d^2\Psi }{dx{\text{'}}^2}-\left(x\text{'}-E\text{'}\right)\Psi =0}$

Haciendo la sustitución ξ=x'-E', llegamos a la ecuación diferencial

${\displaystyle \frac{d^2\Psi (\xi )}{d{\xi }^2}-\xi ·\Psi (\xi )=0}$

Cuya solución es la combinación lineal

Ψ(ξ)=C·Ai(ξ)+D·Bi(ξ)

Ahora bien, Bi(ξ) tiende hacia infinito cuando ξ se hace grande. Sin embargo, Ai(ξ) tiende a cero cuando ξ se hace grande. Se descarta Bi(ξ) de la función de onda.

${\displaystyle \begin{array}{l}\Psi (\xi )=C·\text{Ai}(\xi )\\ \Psi (x\text{'})=C·\text{Ai}(x\text{'}-E\text{'})\\ \Psi (x)=C·\text{Ai}\left(\alpha (mgx-E)\right)\end{array}}$

Donde C es una constante tal que

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}{\Psi }^2(\xi )}·d\xi =1}$

Niveles de energía

Como en x=0 hay una pared infinitamente alta, Ψ(0)=0. En x'=0, Ai(-E')=0. Luego -E' es un cero de la función de Airy Ai(ξ)

La función raices devuelve el vector r de las raíces de la función airy(-x) en el intervalo (0,10)

function airy_1
    x=linspace(0,10,40);
    En=raices(@(x) airy(-x),x);
    disp(En)

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

   2.3381    4.0879    5.5206    6.7867    7.9441    9.0227

Los niveles de energía E tal que αE=E', están al principio muy espaciados y luego, se van juntando a medida que aumenta el número de nivel, n

Funciones de onda

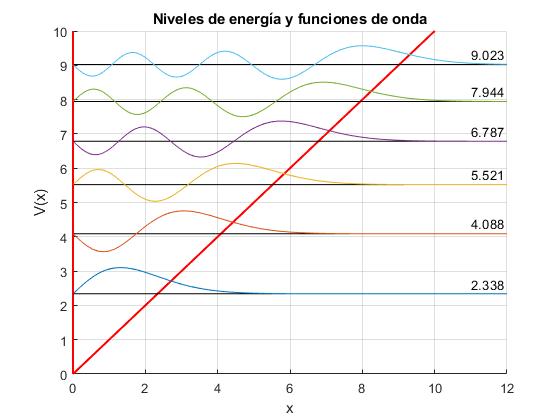
Representamos los primeros niveles de energía E'_n y las correspondientes funciones de onda Ψ(x')=C·Ai(x'-E'_n) para el pozo de potencial

• Para x'=0, V(0)=∞
• Para x'>0, V(x')=x'

El pozo de potencial V(x'), se representa por las líneas gruesas de color rojo

Calcuilamos el coeficiente C de modo que la integral

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}{\left|\psi (x)\right|}^{2}dx}=1}$

Para ello utilizamos la propiedad

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}{\text{Ai}}^2(x)·dx=}\text{Ai}{\text{'}}^2(0)}$

El cuadrado de la derivada de Ai(x) en x=0

function airy_1
    x=linspace(0,10,40);
    En=raices(@(x) airy(-x),x);
    disp(En)
    
    hold on
    line([0,0],[0,12], 'color','r', 'lineWidth',1.5)
    line([0,12],[0,12], 'color','r', 'lineWidth',1.5)
    for i=1:length(En)
        c=1/abs(airy(1,-En(i)));
        line([0,12],[En(i),En(i)],'color','k')
        g=@(x) c*airy(x-En(i))+En(i);
        fplot(g,[0,12])
        text(11,En(i)+0.3,sprintf('%1.3f',En(i)))
    end
    hold off
    ylim([0,10])
    grid on
    xlabel('x')
    ylabel('V(x)')
    title('Niveles de energía y funciones de onda')
    
    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

Potencial en forma de V

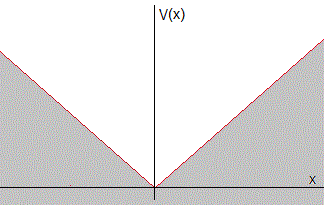
Estudiamos los niveles de energía y las funciones de onda de una partícula de masa m que se mueve en un potencial V(x) en forma de V:

• -mgx para x<0
• mgx para x≥0

Resolvemos la ecuación Schrödinger para x>0, como en el apartado anterior

${\displaystyle \Psi (x\text{'})=C·\text{Ai}(x\text{'}-E\text{'})}$

Utilizamos las propiedades de simetría. Como apreciamos en el pozo de potencial o en el oscilador armónico.

• Las funciones de onda antisimétricas, se anulan en el origen, Ai(-E')=0

x=linspace(0,10,20);
f=@(x) airy(-x); %función Ai(x)
disp(raices(f,x))

    2.3381    4.0879    5.5206    6.7867    7.9441    9.0227

• Las funciones de onda simétricas, presentan un máximo o mínimo en el origen, por lo que su derivada se anula en el origen, Ai'(-E')=0

x=linspace(0,10,20);
f=@(x) airy(1,-x); %derivada de Ai(x)
disp(raices(f,x))

   1.0188    3.2482    4.8201    6.1633    7.3722    8.4885    9.5354

Unimos las dos porciones de código y ordenamos mediante sort los niveles de energía E'_n y los guardamos en el vector En

function airy_2
    x=linspace(0,6,20);
    r1=raices(@(x) airy(-x),x); %función Ai(x)
    r2=raices(@(x) airy(1,-x),x); %derivada de Ai(x)
    En=sort([r1,r2]);
    disp(En)
 
    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

    1.0188    2.3381    3.2482    4.0879    4.8201    5.5206

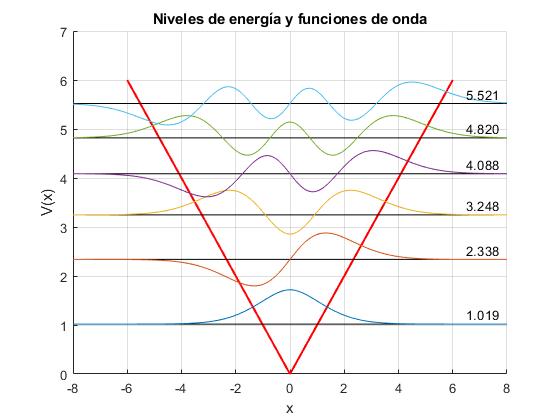
Añadimos al código anterior, la representación de los niveles de energía y las correspondientes funciones de onda

function airy_2
    x=linspace(0,6,20);
    r1=raices(@(x) airy(-x),x); %función Ai(x)
    r2=raices(@(x) airy(1,-x),x); %derivada de Ai(x)
    En=sort([r1,r2]);
    disp(En)
    hold on
    line([0,-6],[0,6], 'color','r', 'lineWidth',1.5)
    line([0,6],[0,6], 'color','r', 'lineWidth',1.5)
    for i=1:length(En)
        f=@(x) airy(x-En(i)).^2;
        c=1/sqrt(2*integral(f,0,50)); %por simetría
        line([-8,8],[En(i),En(i)],'color','k')
        g=@(x) c*airy(x-En(i));
        x=linspace(0,8,100);
        y=g(x);
        if rem(i,2)==1 %si es par i=1,3,5
            yy=[fliplr(y)+En(i),y+En(i)];
        else %si es impar
            yy=[-fliplr(y)+En(i),y+En(i)];
        end 
        plot([-fliplr(x),x],yy)
        text(6.5,En(i)+0.2,sprintf('%1.3f',En(i)))
    end
    hold off
    ylim([0,7])
    grid on
    xlabel('x')
    ylabel('V(x)')
    title('Niveles de energía y funciones de onda')

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

Referencias.

G. Yoder. Using classical probability functions to illuminate the relation between classical and quantum physics. Am. J. Phys. 74 (5), May 2006, pp. 407-408

http://www.physics.csbsju.edu/QM/fall.03.html y http://www.physics.csbsju.edu/QM/fall.04.html

Salma Abdullah, S Alshehri. Properties of Airy function and application to the V-shape potential. Multi-Knowledge Electronic Comprehensive Journal For Education And Science Publications (MECSJ). ISSUE (15), Dec (2018)