Masa del cuerpo celeste

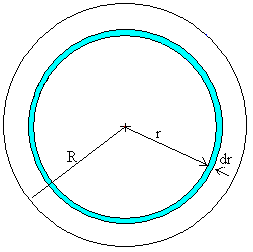
Supongamos un cuerpo celeste de masa M y radio R cuya densidad ρ(r) cambia con la distancia al centro.

Dividimos la esfera de radio R en capas esféricas de radio r y de espesor dr. La masa dm que contiene cada una de las capas es

${\displaystyle dm=\rho (r)\left(4\pi r^{2}dr\right)}$

La masa M(r) contenida en una esfera de radio r es

${\displaystyle M(r)=4\pi {\displaystyle \underset{0}{\overset{r}{\int }}\rho (r)r^{2}dr}}$

Cuando el límite superior es R tenemos la masa M del cuerpo celeste

Cuando la densidad es constante

${\displaystyle \rho =\frac{M}{\frac{4}{3}\pi R^3}}$

Presión en el centro

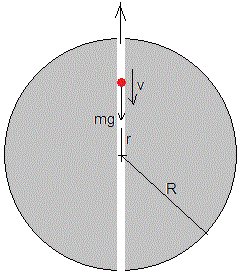
En una capa esférica de de radio r y de espesor dr, consideramos un elemento de volumen (en color rojo) de área dA. Las fuerzas sobre el elemento de masa dm=ρ·dA·dr son

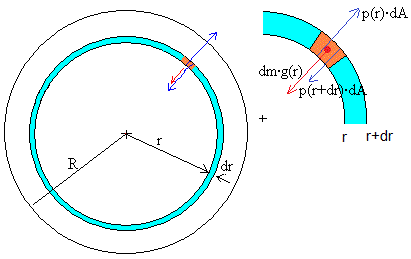
• La fuerza de atracción, dirigida hacia el centro de la Tierra dm·g(r). Donde g(r) es la aceleración de la gravedad a una distancia r del centro de la Tierra

• La fuerza que ejerce la presión p(r)·dA sobre la cara inferior del elemento de volumen

• La fuerza que ejerce la presión p(r+dr)·dA sobre la cara superior del elemento de volumen

En el equilibrio

${\displaystyle \begin{array}{l}\left(p\left(r+dr\right)-p(r)\right)dA=-g(r)\left(\rho (r)dA·dr\right)\\ dp=-g(r)\rho (r)·dr\end{array}}$

Que hemos deducido en la página titulada Esfera de gas en equilibrio bajo la acción de su propia gravedad

${\displaystyle \frac{dp}{dr}=-g(r)\rho (r)}$

Presión en el centro de la Tierra

Suponiendo que la densidad es constante. La aceleración de la gravedad en un punto del interior de la Tierra a una distancia r de su centro es

${\displaystyle g(r)=GM\frac{r}{R^3}}$

La presión a una distancia r del centro de la Tierra es

${\displaystyle p_0-p=-{\displaystyle \underset{r}{\overset{R}{\int }}\frac{M}{\frac{4}{3}\pi R^3}GM\frac{r}{R^3}dr}=-\frac{3G{M}^2}{8\pi R^6}(R^2-r^2)}$

donde p₀=1.013·10⁵ Pa es la presión para r=R es decir, la presión atmosférica

En el centro de la Tierra r=0.

${\displaystyle p=p_{0`}+\frac{3G{M}^2}{8\pi R^4}=1.73·{10}^{11}\text{Pa}}$

Con G=6.67·10^-11 Nm²/kg², R=6.37·10⁶ m, M=5.98·10²⁴ kg

La presión atmosférica es despreciable frente a la presión en el centro de una distribución esférica y uniforme de masa.

Relación entre presión y densidad

Supondremos que la presión p(r) y la densidad ρ(r) están relacionadas. Una ecuación similar a la de un proceso politrópico

${\displaystyle p=K{\rho }^{(n+1)/n}}$

La densidad se expresa

${\displaystyle \rho (r)={\rho }_c{\theta }^n(r)}$

Para r=0, ρ=ρ_c, por lo que θ(0)=1

La presión p(r) es, entonces

${\displaystyle p(r)=K{\rho }^{1+1/n}=K{\rho }_c^{1+1/n}{\theta }^{n+1}(r)}$

La presión en el centro, r=0

${\displaystyle p_c=K{\rho }_c^{1+1/n}}$

La presión p(r) se expresa

${\displaystyle p(r)=p_c{\theta }^{n+1}(r)}$

Ecuación Lane-Emden

La aceleración de la gravedad g(r) en un punto situado a una distancia r del centro, se debe (ley de Gauss) a la masa M(r) contenida en la esfera de radio r

${\displaystyle \begin{array}{l}g(r)=\frac{GM(r)}{r^2}\\ \frac{dp}{dr}=-\rho (r)\frac{GM(r)}{r^2}\end{array}}$

La ecuación diferencial que relaciona presión y densidad se convierte

${\displaystyle \begin{array}{l}\frac{r^2}{\rho }\frac{dp}{dr}=-GM(r)\\ \frac{d}{dr}\left(\frac{r^2}{\rho }\frac{d\left(K{\rho }_c^{1+1/n}{\theta }^{n+1}\right)}{dr}\right)=-4\pi G{r}^2\rho \\ \frac{1}{r^2}\frac{d}{dr}\left(\frac{r^2}{{\rho }_c{\theta }^n}K{\rho }_c^{1+1/n}(n+1){\theta }^n\frac{d\theta }{dr}\right)=-4\pi G{\rho }_c{\theta }^n\\ \frac{(n+1)K{\rho }_c^{-1+1/n}}{4\pi G}\frac{1}{r^2}\frac{d}{dr}\left(r^2\frac{d\theta }{dr}\right)=-{\theta }^n\end{array}}$

Hemos derivado respecto de r, teniendo en cuenta que dM(r)/dr=4πr²ρ(r)

Se define una variable ξ tal que r=αξ

${\displaystyle \begin{array}{l}\frac{(n+1)K{\rho }_c^{-1+1/n}}{4\pi G}\frac{1}{{\alpha }^2}\frac{1}{{\xi }^2}\frac{d}{d\xi }\left({\xi }^2\frac{d\theta }{d\xi }\right)=-{\theta }^n\\ \frac{1}{{\xi }^2}\frac{d}{d\xi }\left({\xi }^2\frac{d\theta }{d\xi }\right)=-{\theta }^n,\alpha =\sqrt{\frac{(n+1)K{\rho }_c^{-1+1/n}}{4\pi G}}\end{array}}$

Esta es la ecuación de Lane-Emden que resolveremos con las condiciones iniciales

• De la función θ en ξ=0

${\displaystyle \xi =\mathrm{0,}\theta =1}$

• De la derivada primera, dθ/dξ en ξ=0

${\displaystyle \frac{d\rho }{dr}=n{\rho }_c{\theta }^{n-1}\frac{d\theta }{dr},\frac{d\theta }{dr}=\frac{1}{n{\rho }_c{\theta }^{n-1}}\frac{d\rho }{dr},\frac{d\theta }{d\xi }=\frac{\alpha }{n{\rho }_c{\theta }^{n-1}}\frac{d\rho }{dr}}$

La densidad es máxima dρ/dr=0 en el centro, r=0, ξ=0

${\displaystyle \frac{d\theta }{d\xi }=\mathrm{0,}\xi =0}$

Otra forma de argumentarlo es la siguiente. En la ecuación

${\displaystyle \frac{dp}{dr}=-\rho (r)\frac{GM(r)}{r^2}}$

M(r) es proporcional a r³, el cociente es proporcional a r, cuando r→0, dp/dr→0. Como p=Kρ^(1+1/n). Si dp/dr→0 cuando r→0, entonces dρ/dr→0.

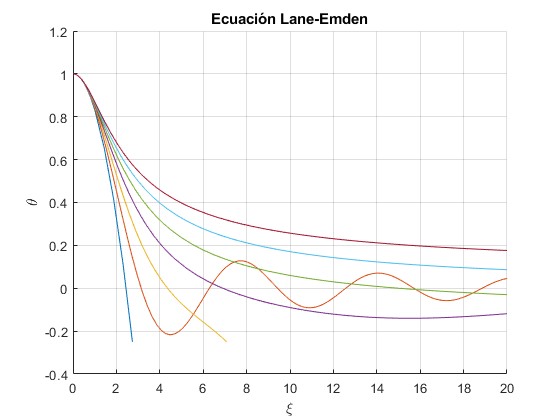
Representamos las soluciones numéricas, empleando el procedimiento ode45 de MATLAB, de la ecuación de Lane-Emden para n=0, 1, 2, 3, 4, 5, 6.

${\displaystyle \frac{d^2\theta }{d{\xi }^2}+\frac{2}{\xi }\frac{d\theta }{d\xi }+{\theta }^n=0}$

Observamos que algunas cortan al eje horizontal ξ en un punto, en varios puntos o en ninguno. El primer punto de corte es significativo, su abscisa es ξ₁

function politropico_9
    opts=odeset('events',@stop_politropico);
    hold on  
    for n=0:6
        fg=@(t,x)[x(2);-2*x(2)/t-x(1)^n];
        [t,x]=ode45(fg,[eps,20],[1,eps],opts);
        plot(t,x(:,1))
    end
    hold off
    grid on
    xlabel('\xi')
    ylabel('\theta');
    title('Ecuación Lane-Emden')
 
    function [value,isterminal,direction]=stop_politropico(~,x)
       %x(1) es  x, x(3) es y
        value=x(1)+0.25;
        isterminal=1;   
        direction=-1; 
    end
end

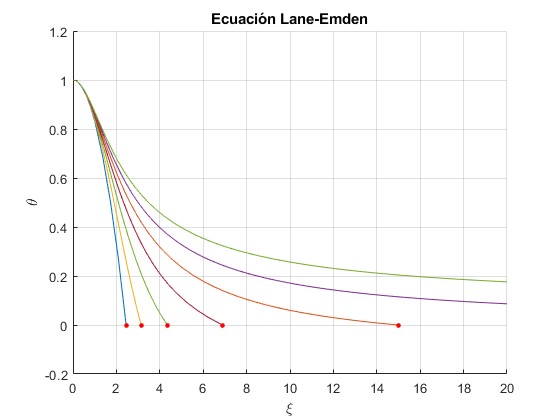
Representamos dichas soluciones numéricas, hasta el primer punto de corte con el eje horizontal (punto de color rojo) si lo tuviera

function politropico_6
    opts=odeset('events',@stop_politropico);
    hold on  
    for n=0:6
        fg=@(t,x)[x(2);-2*x(2)/t-x(1)^n];
        [t,x, te, xe]=ode45(fg,[eps,20],[1,eps],opts);
        plot(t,x(:,1))
        if te
            plot(te,0,'ro','markersize',3,'markerfacecolor','r')
            disp([n,te, xe(2)])
        end
    end
    hold off
    grid on
    xlabel('\xi')
    ylabel('\theta');
    title('Ecuación Lane-Emden')
    
    function [value,isterminal,direction]=stop_politropico(~,x)
        value=x(1);
        isterminal=1;   
        direction=-1; 
    end

end

        0    2.4495   -0.8165
    1.0000    3.1420   -0.3182
    2.0000    4.3541   -0.1271
    3.0000    6.9009   -0.0424
    4.0000   15.0052   -0.0080

La tabla recoge los datos de la abscisa ξ₁ del punto de corte con el eje horizontal y de la pendiente de la curva θ(ξ) en dicho punto. Datos que precisaremos más adelante

Masa y radio del cuerpo celeste

En la superficie del cuerpo celeste r=R, la densidad ρ(r) se anula, R=αξ₁, θ(ξ₁)=0. Por tanto, ξ₁ es el primer cero de la función θ(ξ)

La masa M vale

${\displaystyle M=4\pi {\displaystyle \underset{0}{\overset{R}{\int }}\rho (r)r^{2}dr}=4\pi {\rho }_c{\alpha }^3{\displaystyle \underset{0}{\overset{{\xi }_1}{\int }}{\xi }^2{\theta }^{n}d\xi },{\xi }_1=\frac{R}{\alpha }}$

Por la ecuación de Lane-Emden

${\displaystyle {\xi }^2{\theta }^n=-\frac{d}{d\xi }\left({\xi }^2\frac{d\theta }{d\xi }\right)}$

La masa del cuerpo celeste se expresa en términos de ξ₁ y de la derivada dθ/dξ para ξ=ξ₁

${\displaystyle \begin{array}{l}M=4\pi {\rho }_c{\alpha }^3{\displaystyle \underset{0}{\overset{{\xi }_1}{\int }}{\xi }^2{\theta }^{n}d\xi }=-4\pi {\rho }_c{\alpha }^3{\displaystyle \underset{0}{\overset{{\xi }_1}{\int }}d\left({\xi }^2\frac{d\theta }{d\xi }\right)}=-4\pi {\rho }_c{\alpha }^3{\xi }_1^2{\left(\frac{d\theta }{d\xi }\right)}_{{\xi }_1}\\ M=-4\pi {\rho }_c{\left(\frac{(n+1)K{\rho }_c^{-1+1/n}}{4\pi G}\right)}^{3/2}{\xi }_1^2{\left(\frac{d\theta }{d\xi }\right)}_{{\xi }_1}\\ M=-\frac{{\left(n+1\right)}^{3/2}}{\sqrt{4\pi }}{\left(\frac{K}{G}\right)}^{3/2}{\rho }_c^{\frac{3-n}{2n}}{\xi }_1^2{\left(\frac{d\theta }{d\xi }\right)}_{{\xi }_1}\end{array}}$

Relación entre masa M y radio R

${\displaystyle \begin{array}{l}M=-4\pi {\rho }_c{\alpha }^3{\xi }_1^2{\left(\frac{d\theta }{d\xi }\right)}_{{\xi }_1},R={\xi }_1\alpha \\ {\alpha }^2=\frac{(n+1)K{\rho }_c^{-1+1/n}}{4\pi G},{\rho }_c^{\frac{1-n}{n}}=\frac{4\pi G{\alpha }^2}{(n+1)K},{\rho }_c={\left(\frac{(n+1)K}{4\pi G{\alpha }^2}\right)}^{\frac{n}{n-1}}\\ M=-4\pi {\left(\frac{(n+1)K}{4\pi G{\alpha }^2}\right)}^{\frac{n}{n-1}}{\alpha }^3{\xi }_1^2{\left(\frac{d\theta }{d\xi }\right)}_{{\xi }_1}=-4\pi {\left(\frac{(n+1)K}{4\pi G}\right)}^{\frac{n}{n-1}}{\left(\frac{R}{{\xi }_1}\right)}^{\frac{n-3}{n-1}}{\xi }_1^2{\left(\frac{d\theta }{d\xi }\right)}_{{\xi }_1}\\ 4\pi {\left(-\frac{M}{{\xi }_1^2{\left(\frac{d\theta }{d\xi }\right)}_{{\xi }_1}}\right)}^{n-1}={\left(\frac{(n+1)K}{G}\right)}^n{\left(\frac{R}{{\xi }_1}\right)}^{n-3}\\ M^{n-1}\sim R^{n-3}\end{array}}$

Dos casos son importantes

Otra característica importante, es el cociente entre las densidad y la densidad media

${\displaystyle \begin{array}{l}{D}_n=\frac{{\rho }_c}{<\rho >},<\rho >=\frac{M}{\frac{4}{3}\pi R^3}\\ D_n={\rho }_c\frac{4\pi R^3}{3M}={\rho }_c\frac{4\pi R^3}{3M}=-{\rho }_c\frac{4\pi {\alpha }^3{\xi }_1^3}{3·4\pi {\rho }_c{\alpha }^3{\xi }_1^2\left(\frac{d\theta }{d\xi }\right)}=-\frac{{\xi }_1}{3{\left(\frac{d\theta }{d\xi }\right)}_{{\xi }_1}}\end{array}}$

Soluciones analíticas

La ecuación de Lane-Emden tiene soluciones analíticas para n=0, 1 y 5

n=0

Para n=0, la densidad es constante e igual a la densidad ρ_c. La solución de la ecuación Lane-Emden es sencilla

${\displaystyle \begin{array}{l}\frac{1}{{\xi }^2}\frac{d}{d\xi }\left({\xi }^2\frac{d\theta }{d\xi }\right)=-1\\ \frac{d}{d\xi }\left({\xi }^2\frac{d\theta }{d\xi }\right)=-{\xi }^2\\ {\xi }^2\frac{d\theta }{d\xi }=-\frac{{\xi }^3}{3}+c_1\\ \frac{d\theta }{d\xi }=-\frac{\xi }{3}+\frac{c_1}{{\xi }^2}\\ \theta =-\frac{{\xi }^2}{6}-\frac{c_1}{\xi }+c_2\end{array}}$

Las constantes c₁ y c₂ se determinan a partir de las condiciones iniciales

ξ=0, θ=1

c₁=0, c₂=1

${\displaystyle \theta =1-\frac{{\xi }^2}{6}}$

Se cumple la segunda condición inicial, que dθ/dξ=0 para ξ=0

La función se anula θ(ξ)=0 para ${\xi }_1=\sqrt{6}$. El radio del cuerpo celeste es, $R=\sqrt{6}\alpha$

La presión es

${\displaystyle \begin{array}{l}p=p_c\theta (\xi )=p_c\left(1-\frac{{\xi }^2}{6}\right)=p_c\left(1-\frac{r^2}{6{\alpha }^2}\right)\\ p(r)=p_c\left(1-\frac{r^2}{R^2}\right)\end{array}}$

Como la densidad es constante ρ_c, la presión en el centro se calcula integrando

${\displaystyle \begin{array}{l}\frac{dp}{dr}=-\rho (r)\frac{GM(r)}{r^2}\\ \frac{dp}{dr}=-{\rho }_c\frac{G{\rho }_c\frac{4}{3}\pi r^3}{r^2}\\ {\displaystyle \underset{p_c}{\overset{0}{\int }}dp}=-\frac{4\pi }{3}G{\rho }_c^2{\displaystyle \underset{0}{\overset{R}{\int }}r·dr}\\ p_c=\frac{2\pi }{3}G{\rho }_c^2{R}^2\end{array}}$

n=1

La ecuación de Lane-Emden para n=1

${\displaystyle \begin{array}{l}\frac{1}{{\xi }^2}\frac{d}{d\xi }\left({\xi }^2\frac{d\theta }{d\xi }\right)=-\theta \\ {\xi }^2\frac{d^2\theta }{d{\xi }^2}+2\xi \frac{d\theta }{d\xi }+{\xi }^2\theta =0\end{array}}$

Es la ecuación diferencial de las funciones esféricas de Bessel.

${\displaystyle x^2\frac{d^{2}y}{d{x}^2}+2x\frac{dy}{dx}+\left(x^2-n(n+1)\right)y=0}$

La solución de esta ecuación diferencial para n=0 es

${\displaystyle \begin{array}{l}y(x)=A·j_0(x)+B·y_0(x)\\ j_0(x)=\frac{\sin x}{x},y_0(x)=-\frac{\cos x}{x}\end{array}}$

La solución de la ecuación de Lane_Emden

${\displaystyle \theta (\xi )=\frac{\sin \xi }{\xi }}$

B=0, ya que cosξ/ξ tiende a ∞ cuando ξ→0. Esta solución cumple las condiciones iniciales

${\displaystyle \begin{array}{l}\underset{\xi \to 0}{\lim }\frac{\sin \xi }{\xi }=1\\ \frac{d\theta }{d\xi }=\frac{\xi \cos \xi -\sin \xi }{{\xi }^2}\\ {\left(\frac{d\theta }{d\xi }\right)}_{\xi =0}=0\end{array}}$

El primer cero de esta función es ξ₁=π

El parámetro α para n=1

${\displaystyle \alpha =\sqrt{\frac{K}{2\pi G}}}$

La presión en el centro es

${\displaystyle \begin{array}{l}{p}_c=K{\rho }_c^2\\ {\alpha }^2=\frac{p_c}{2\pi G{\rho }_c^2},\frac{R^2}{{\pi }^2}=\frac{p_c}{2\pi G{\rho }_c^2}\\ p_c=\frac{2G}{\pi }{\rho }_c^2{R}^2\end{array}}$

La presión p(r)

${\displaystyle \begin{array}{l}\theta (r)=\frac{\sin \left(\pi \frac{r}{R}\right)}{\pi \frac{r}{R}}=\frac{R}{\pi r}\sin \left(\pi \frac{r}{R}\right)\\ p(r)=p_c{\theta }^2(r)=p_c{\left(\frac{R}{\pi r}\sin \left(\pi \frac{r}{R}\right)\right)}^2\end{array}}$

La densidad

${\displaystyle \begin{array}{l}\rho ={\rho }_c\theta \\ \rho (r)={\rho }_c\frac{R}{\pi r}\sin \left(\pi \frac{r}{R}\right)\end{array}}$

La masa

${\displaystyle \begin{array}{l}M=-4\pi {\rho }_c{\alpha }^3{\xi }_1^2{\left(\frac{d\theta }{d\xi }\right)}_{{\xi }_1}\\ M=-4\pi {\rho }_c{\left(\frac{R}{\pi }\right)}^3{\pi }^2{\left(\frac{d\theta }{d\xi }\right)}_{{\xi }_1}\end{array}}$

Nos queda por calcular el valor de la derivada de θ(ξ) en ξ₁=π

${\displaystyle \begin{array}{l}\frac{d\theta }{d\xi }=\frac{\xi \cos \xi -\sin \xi }{{\xi }^2}\\ {\frac{d\theta }{d\xi }|}_{\xi =\pi }=\frac{-\pi }{{\pi }^2}=-\frac{1}{\pi }\end{array}}$

El resultado es

${\displaystyle M=-4\pi {\rho }_c{\left(\frac{R}{\pi }\right)}^3{\pi }^2\frac{-1}{\pi }=\frac{4}{\pi }{\rho }_c{R}^3}$

El radio R

${\displaystyle \begin{array}{l}{p}_c=\frac{2G}{\pi }{\rho }_c^2{R}^2\\ R=\sqrt{\frac{\pi p_c}{2G{\rho }_c^2}=}\sqrt{\frac{\pi K{\rho }_c^2}{2G{\rho }_c^2}}=\sqrt{\frac{\pi K}{2G}}\end{array}}$

es independiente de la masa M

n=5

Se ha encontrado solución analítica a la ecuación diferencial

${\displaystyle \frac{1}{{\xi }^2}\frac{d}{d\xi }\left({\xi }^2\frac{d\theta }{d\xi }\right)=-{\theta }^5}$

Es complicado deducir la solución de esta ecuación diferencial, Véase

Chandrasekhar, S. An Introduction to the Study of Stellar Structure. New York: Dover, pp. 84-182, 1967.

${\displaystyle \theta =\frac{1}{\sqrt{1+\frac{1}{3}{\xi }^2}}}$

La densidad es

${\displaystyle \begin{array}{l}\rho (r)={\rho }_c{\theta }^n\\ \rho (r)={\rho }_c{\left(1+\frac{1}{3}{\xi }^2\right)}^{-5/2}\end{array}}$

No hay corte ξ₁ con el eje horizontal, ya que θ→0 cuando ξ→∞. El radio es por tanto, infinito. Sin embargo, la masa es finita

${\displaystyle M=-\frac{{\left(n+1\right)}^{3/2}}{\sqrt{4\pi }}{\left(\frac{K}{G}\right)}^{3/2}{\rho }_c^{\frac{3-n}{2n}}{\xi }_1^2{\left(\frac{d\theta }{d\xi }\right)}_{{\xi }_1}}$

El límite cuando ξ→∞, del producto de los dos últimos términos

${\displaystyle \begin{array}{l}{\xi }^2\frac{d\theta }{d\xi }=-\frac{{\xi }^3}{3{\left(1+\frac{1}{3}{\xi }^2\right)}^{3/2}}\\ -\frac{1}{3}\underset{\xi \to \infty }{\lim }\left(\frac{{\xi }^3}{{\left(1+\frac{1}{3}{\xi }^2\right)}^{3/2}}\right)=-\frac{1}{3}\underset{\xi \to \infty }{\lim }\left(\frac{1}{{\left(\frac{1}{{\xi }^2}+\frac{1}{3}\right)}^{3/2}}\right)=-\frac{3^{3/2}}{3}=-\sqrt{3}\end{array}}$

La masa M es

${\displaystyle M=\frac{6^{3/2}}{\sqrt{4\pi }}{\left(\frac{K}{G}\right)}^{3/2}{\rho }_c^{-\frac{1}{5}}\sqrt{3}=3^2\sqrt{\frac{2}{\pi }}{\left(\frac{K}{G}\right)}^{3/2}{\rho }_c^{-\frac{1}{5}}}$

La presión en el centro es

${\displaystyle \begin{array}{l}{p}_c=K{\rho }_c^{1+1/n}\\ p_c=K{\rho }_c^{6/5}\end{array}}$

En términos de la masa M

${\displaystyle \begin{array}{l}{M}^2=3^4\frac{2}{\pi }{\left(\frac{K}{G}\right)}^3{\rho }_c^{-2/5}\\ p_c={\left(\frac{\pi M^2{G}^3}{3^4·2}\right)}^{1/3}{\rho }_c^{4/3}\end{array}}$

Representamos las soluciones analíticas de la ecuación diferencial de Lane-Emden

hold on
fplot(@(x) 1-x.^2/6, [0,sqrt(6)])
fplot(@(x) sin(x)./x, [0,pi])
fplot(@(x) 1./sqrt(1+x.^2/3), [0,10])
hold off
grid on
xlabel('\xi')
ylabel ('\theta')
legend('n=0','n=1','n=5', 'location','best')
title('Soluciones analíticas')

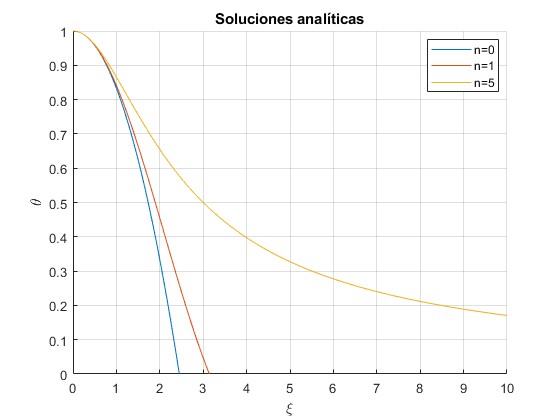
Las abscisas de los puntos de corte con el eje horizontal son, para n=0, ξ₁=$\sqrt{6}$, para n=1, ξ₁=π.

Procedimiento numérico

Comprobamos que el procedimiento de Runge-Kutta resuelve la ecuación diferencial de Lane-Emden para los casos que tiene solución analítica. Este procedimiento parece más adecuado que las diversas veriones ode?? de MATLAB

Para mejorar los resultados, calculamos ξ₁ y (dθ/dξ)_ξ1 mediante interpolación lineal, del siguiente modo

${\displaystyle \xi =\frac{{\theta }_k{\xi }_{k+1}-{\theta }_{k+1}{\xi }_k}{{\theta }_k-{\theta }_{k+1}},v=\frac{v_k\left({\xi }_{k+1}-\xi \right)+v_{k+1}\left(\xi -{\xi }_k\right)}{{\xi }_{k+1}-{\xi }_k}}$

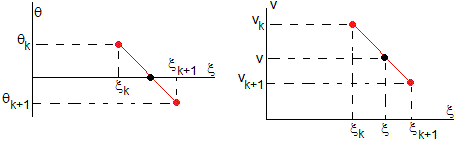
Donde el símbolo v significa dθ/dξ

function politropico_8
    hold on
    for n=[0,1,5]
        f=@(t,x,v) -2*v/t-x^n;
        [t,x,~,k1]=rk_2(f,eps,20,1,eps,200);
        x=x(1:k1);
        t=t(1:k1);
        plot(t,x)
    end
    fplot(@(x) 1-x.^2/6, [0,sqrt(6)]) %soluciones analíticas
    fplot(@(x) sin(x)./x, [0,pi])
    fplot(@(x) 1./sqrt(1+x.^2/3), [0,20])
    hold off
    grid on
    xlabel('\xi')
    ylabel('\theta');
    title('Ecuación de Lane-Emden')

    function [t,x,v, k1] =rk_2(f,t0,tf,x0,v0,n)
          h=(tf-t0)/n;
          t=t0:h:tf;
          x=zeros(n+1,1); 
          v=zeros(n+1,1);
          x(1)=x0; v(1)=v0;
          
          for k=1:n
            k1=h*v(k);
            l1=h*f(t(k),x(k),v(k));
            k2=h*(v(k)+l1/2);
            l2=h*f(t(k)+h/2,x(k)+k1/2,v(k)+l1/2);
            k3=h*(v(k)+l2/2);
            l3=h*f(t(k)+h/2,x(k)+k2/2,v(k)+l2/2);
            k4=h*(v(k)+l3);
            l4=h*f(t(k)+h,x(k)+k3,v(k)+l3);
            
            x(k+1)=x(k)+(k1+2*k2+2*k3+k4)/6;
            v(k+1)=v(k)+(l1+2*l2+2*l3+l4)/6;        
            if x(k+1)<=0
                 %interpolación
                 k1=k+1;
                 t1=(x(k)*t(k+1)-x(k+1)*t(k))/(x(k)-x(k+1));
                 v1=(v(k)*(t(k+1)-t1)+v(k+1)*(t1-t(k)))/(t(k+1)-t(k));
                 t(k+1)=t1;
                 x(k+1)=0;
                  v(k+1)=v1;
                 disp([t1,v1])
                break;
            end
          end
    end
end

    2.4482   -0.8158
    3.1438   -0.3178

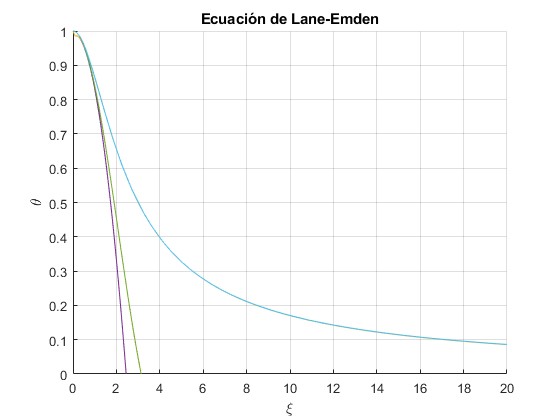
La solución analítica y numérica de la ecuación diferencial coinciden

Viaje a través de un túnel que atraviesa un cuerpo celeste

Densidad

${\displaystyle \frac{\rho (r)}{{\rho }_c}={\theta }^n(r)}$

Analítica para n=0, 1, 5

${\displaystyle \begin{array}{l}n=\mathrm{0,}\frac{\rho }{{\rho }_c}=1\\ n=\mathrm{1,}\frac{\rho }{{\rho }_c}=\frac{\sin \xi }{\xi }\\ n=\mathrm{5,}\frac{\rho }{{\rho }_c}={\left(1+\frac{1}{3}{\xi }^2\right)}^{-5/2}\end{array}}$

hold on
line([0,sqrt(6)],[1,1])
fplot(@(x) sin(x)./x, [0,pi])
fplot(@(x) 1./sqrt(1+x.^3/3).^5, [0,4])
hold off
grid on
xlabel('\xi')
ylabel('\rho/\rho_c')
ylim([0,1.02])
legend('0','1','5','Location','best')
title('Densidad')

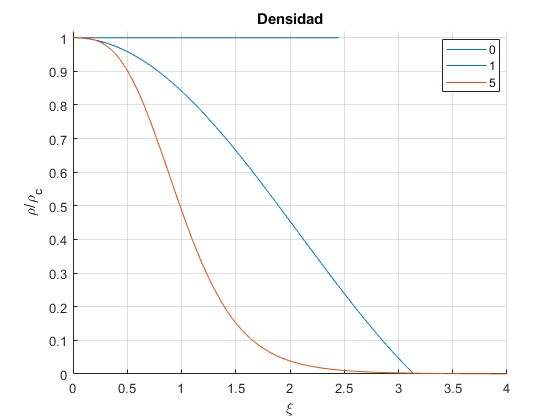
Para n=0, la densidad es constante e igual a ρ_c

Numérica

Representamos la densidad ρ/ρ_c en función de r/R o bien, de ξ/ξ₁ para n=0, 1, 1.5, 3.

function politropico_11
    hold on
    for n=[0,1,1.5,3]
        f=@(t,x,v) -2*v/t-x^n;
        [t,x,~,k1]=rk_2(f,eps,20,1,eps,200);
        x=x(1:k1);
        t=t(1:k1);
        plot(t/t(end),x.^n)
    end
    hold off
    grid on
    xlabel('r/R')
    ylabel('\rho/\rho_c');
    ylim([0,1.02])
    legend('0','1','1.5','3','Location','best')
    title('Densidad')

    function [t,x,v, k1] =rk_2(f,t0,tf,x0,v0,n)
          h=(tf-t0)/n;
          t=t0:h:tf;
          x=zeros(n+1,1); 
          v=zeros(n+1,1);
          x(1)=x0; v(1)=v0;
          
          for k=1:n
            k1=h*v(k);
            l1=h*f(t(k),x(k),v(k));
            k2=h*(v(k)+l1/2);
            l2=h*f(t(k)+h/2,x(k)+k1/2,v(k)+l1/2);
            k3=h*(v(k)+l2/2);
            l3=h*f(t(k)+h/2,x(k)+k2/2,v(k)+l2/2);
            k4=h*(v(k)+l3);
            l4=h*f(t(k)+h,x(k)+k3,v(k)+l3);
            
            x(k+1)=x(k)+(k1+2*k2+2*k3+k4)/6;
            v(k+1)=v(k)+(l1+2*l2+2*l3+l4)/6;        
            if x(k+1)<=0
                 %interpolación
                 k1=k+1;
                 t1=(x(k)*t(k+1)-x(k+1)*t(k))/(x(k)-x(k+1));
                 v1=(v(k)*(t(k+1)-t1)+v(k+1)*(t1-t(k)))/(t(k+1)-t(k));
                 t(k+1)=t1;
                 x(k+1)=0;
                v(k+1)=v1;
                break;
            end
          end
    end
end

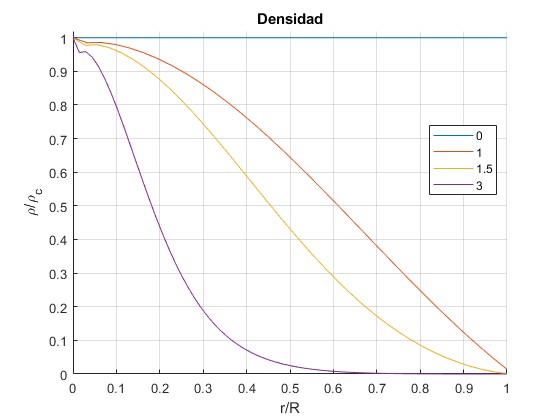
Cuando n es grande, la masa se distribuye alrededor del centro y cada vez más próxima a éste.

Aceleración de la gravedad

La aceleración de la gravedad g(r) en un punto situado a una distancia r del centro, se debe (ley de Gauss) a la masa M(r) contenida en la esfera de radio r

${\displaystyle \begin{array}{l}M(r)=-4\pi {\rho }_c{\alpha }^3{\xi }^2\left(\frac{d\theta }{d\xi }\right),r=\alpha \xi \\ g(r)=G\frac{M(r)}{r^2}=-4\pi G{\rho }_c\alpha \left(\frac{d\theta }{d\xi }\right)\end{array}}$

Supongamos que excavamos un túnel a través de un diámetro del cuerpo celeste. Soltamos la partícula en un extremo del túnel, en la superficie de dicho cuerpo, su velocidad cuando está a una distancia r del centro se calcula aplicando el principio de conservación de la energía

El valor de la aceleración de la gravedad en la superficie de la Tierra es

${\displaystyle g_m=\frac{GM}{R^2}}$

El cociente g(r)/g_m vale

${\displaystyle \frac{g(r)}{g_m}=R^2\frac{4\pi {\rho }_c\alpha \frac{d\theta }{d\xi }}{4\pi {\rho }_c{\alpha }^3{\xi }_1^2{\left(\frac{d\theta }{d\xi }\right)}_{{\xi }_1}}=R^2\frac{\frac{d\theta }{d\xi }}{{\alpha }^2{\xi }_1^2{\left(\frac{d\theta }{d\xi }\right)}_{{\xi }_1}}=\frac{\frac{d\theta }{d\xi }}{{\left(\frac{d\theta }{d\xi }\right)}_{{\xi }_1}}}$

Analítica para n=0, 1

${\displaystyle \begin{array}{l}n=\mathrm{0,}\frac{g}{g_m}=\frac{\xi }{\sqrt{6}}\\ n=\mathrm{1,}\frac{g}{g_m}=-\pi \frac{\xi \cos \xi -\sin \xi }{{\xi }^2}\end{array}}$

hold on
line([0,sqrt(6)],[0,1],'color','r')
fplot(@(x) -pi*(x.*cos(x)-sin(x))./x.^2, [0,pi])
hold off
grid on
xlabel('\xi')
ylabel('g/g_m')
legend('0','1','Location','best')
title('Aceleración de la gravedad')

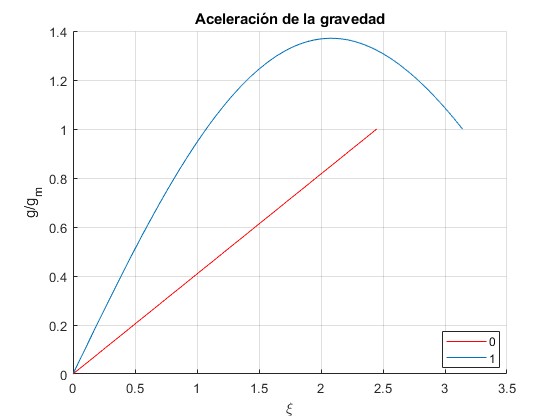
Para n=0, la densidad es constante e igual a ρ_c. La aceleración de la gravedad se incrementa linealmente hasta su valor en la superficie g_m

Numérica

Representamos el cociente g/g_m en función de r/R o bien, de ξ/ξ₁ para n=0, 1, 1.5, 2.

function politropico_12
    hold on
    for n=[0,1,1.5,2]
        f=@(t,x,v) -2*v/t-x^n;
        [t,~,v, k1]=rk_2(f,eps,20,1,eps,200);
        v=v(1:k1);
        t=t(1:k1);
        plot(t/t(end),v/v(end))
    end
    hold off
    grid on
    xlabel('r/R')
    ylabel('g/g_m');
    ylim([-0.1,3])
    legend('0','1','1.5','2','Location','best')
    title('Aceleración de la gravedad')

    function [t,x,v, k1] =rk_2(f,t0,tf,x0,v0,n)
          h=(tf-t0)/n;
          t=t0:h:tf;
          x=zeros(n+1,1); 
          v=zeros(n+1,1);
          x(1)=x0; v(1)=v0;
          
          for k=1:n
            k1=h*v(k);
            l1=h*f(t(k),x(k),v(k));
            k2=h*(v(k)+l1/2);
            l2=h*f(t(k)+h/2,x(k)+k1/2,v(k)+l1/2);
            k3=h*(v(k)+l2/2);
            l3=h*f(t(k)+h/2,x(k)+k2/2,v(k)+l2/2);
            k4=h*(v(k)+l3);
            l4=h*f(t(k)+h,x(k)+k3,v(k)+l3);
            
            x(k+1)=x(k)+(k1+2*k2+2*k3+k4)/6;
            v(k+1)=v(k)+(l1+2*l2+2*l3+l4)/6;        
            if x(k+1)<=0
                 %interpolación
                 k1=k+1;
                 t1=(x(k)*t(k+1)-x(k+1)*t(k))/(x(k)-x(k+1));
                 v1=(v(k)*(t(k+1)-t1)+v(k+1)*(t1-t(k)))/(t(k+1)-t(k));
                 t(k+1)=t1;
                 x(k+1)=0;
                v(k+1)=v1;
                 break;
            end
          end
    end
end

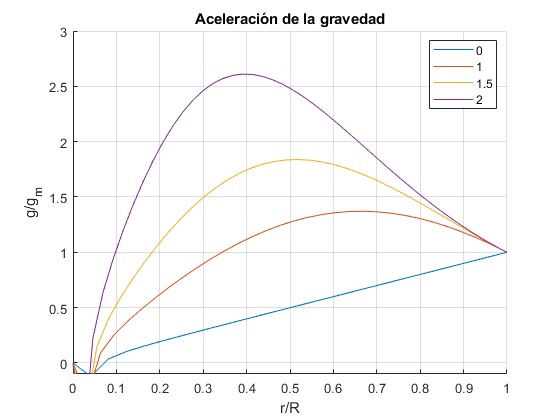
Tiempo de viaje

La fuerza que ejerce el campo gravitatorio producido por el cuerpo celeste sobre una partícula de masa m es el producto de su masa por la aceleración de la gravedad g(r). La aceleración de la gravedad en el interior de dicho cuerpo es M(r)/r² y en el exterior es M/r², siendo M la masa dl cuerpo celeste.

El nivel cero de energía potencial se encuentra en el infinito, de modo que la energía potencial de una partícula de masa m situada a una distancia r del centro, es

${\displaystyle \begin{array}{l}{E}_p(r)={\displaystyle \underset{r}{\overset{R}{\int }}-G\frac{M(r)m}{r^2}dr}+{\displaystyle \underset{R}{\overset{\infty }{\int }}-G\frac{M·m}{r^2}dr}\\ =-{\displaystyle \underset{r}{\overset{R}{\int }}G\frac{M(r)m}{r^2}dr}-G\frac{Mm}{R}\end{array}}$

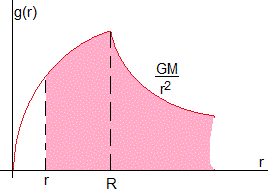
Aplicamos el principio de conservación de la energía y despejamos la velocidad v de la partícula a la distancia r del centro

${\displaystyle \begin{array}{l}\begin{array}{l}\frac{1}{2}m{v}^2+E_p(r)=E_p(R)\hfill \\ v^2=2{\displaystyle \underset{r}{\overset{R}{\int }}G\frac{M(r)}{r^2}dr}=2{\displaystyle \underset{r}{\overset{R}{\int }}g(r)dr=2\alpha {\displaystyle \underset{\xi }{\overset{{\xi }_1}{\int }}g(\xi )d\xi }=-8\pi G{\rho }_c{\alpha }^2{\displaystyle \underset{\xi }{\overset{{\xi }_1}{\int }}\frac{d\theta }{d\xi }d\xi }}\hfill \end{array}\\ v^2=-8\pi G{\rho }_c{\alpha }^2\left(\theta ({\xi }_1)-\theta (\xi )\right)=8\pi G{\rho }_c{\alpha }^2\theta (\xi )\\ v=2\frac{R}{{\xi }_1}\sqrt{2\pi G{\rho }_c\theta (\xi )}\end{array}}$

Como θ(0)=1, la máxima velocidad se alcanza para ξ=0, r=0, en el centro

${\displaystyle \begin{array}{l}{v}_m=2\frac{R}{{\xi }_1}\sqrt{2\pi G{\rho }_c}\\ v(\xi )=v_m\sqrt{\theta (\xi )}\end{array}}$

Analítica para n=0, 1

${\displaystyle \begin{array}{l}n=\mathrm{0,}\frac{v}{v_m}=\sqrt{1-\frac{1}{6}{\xi }^2}\\ n=\mathrm{1,}\frac{v}{v_m}=\sqrt{\frac{\sin \xi }{\xi }}\end{array}}$

hold on
fplot(@(x) sqrt(1-x.^2/6), [0,sqrt(6)])
fplot(@(x) sqrt(sin(x)./x), [0,pi])
hold off
grid on
xlabel('\xi')
ylabel('v/v_m')
legend('0','1','Location','best')
title('Velocidad')

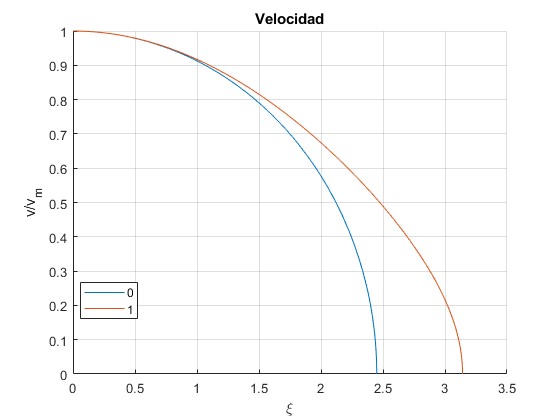
Alcanza la máxima velocidad v_m en el centro del cuerpo celeste (ξ=0).

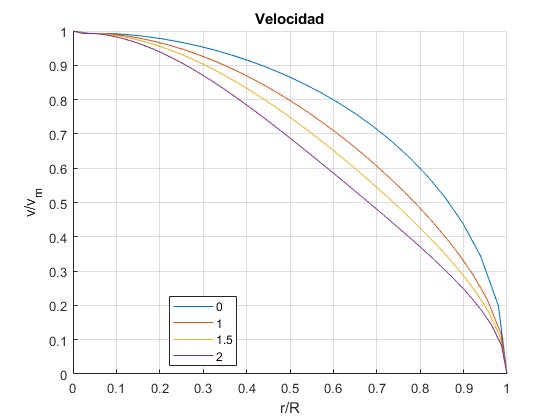
Numérica

Representamos el cociente v/v_m en función de r/R o bien, de ξ/ξ₁ para n=0, 1, 1.5, 2. La partícula parte del reposo en la superficie r=R (ξ₁).

function politropico_13
    hold on
    for n=[0,1,1.5,2]
        f=@(t,x,v) -2*v/t-x^n;
        [t,x,~, k1]=rk_2(f,eps,20,1,eps,200);
        x=x(1:k1);
        t=t(1:k1);
        plot(t/t(end),sqrt(x))
    end
    hold off
    grid on
    xlabel('r/R')
    ylabel('v/v_m');
    legend('0','1','1.5','2','Location','best')
    title('Velocidad')

    function [t,x,v, k1] =rk_2(f,t0,tf,x0,v0,n)
          h=(tf-t0)/n;
          t=t0:h:tf;
          x=zeros(n+1,1); 
          v=zeros(n+1,1);
          x(1)=x0; v(1)=v0;
          
          for k=1:n
            k1=h*v(k);
            l1=h*f(t(k),x(k),v(k));
            k2=h*(v(k)+l1/2);
            l2=h*f(t(k)+h/2,x(k)+k1/2,v(k)+l1/2);
            k3=h*(v(k)+l2/2);
            l3=h*f(t(k)+h/2,x(k)+k2/2,v(k)+l2/2);
            k4=h*(v(k)+l3);
            l4=h*f(t(k)+h,x(k)+k3,v(k)+l3);
            
            x(k+1)=x(k)+(k1+2*k2+2*k3+k4)/6;
            v(k+1)=v(k)+(l1+2*l2+2*l3+l4)/6;        
            if x(k+1)<=0
                 %interpolación
                 k1=k+1;
                 t1=(x(k)*t(k+1)-x(k+1)*t(k))/(x(k)-x(k+1));
                 v1=(v(k)*(t(k+1)-t1)+v(k+1)*(t1-t(k)))/(t(k+1)-t(k));
                 t(k+1)=t1;
                 x(k+1)=0;
                  v(k+1)=v1;
                break;
            end
          end
    end
end

El tiempo que tarda en viajar desde la superficie hasta el centro, es

${\displaystyle T_0={\displaystyle \underset{0}{\overset{R}{\int }}\frac{dr}{v(r)}}=\alpha {\displaystyle \underset{0}{\overset{{\xi }_1}{\int }}\frac{d\xi }{v(\xi )}}=\alpha {\displaystyle \underset{0}{\overset{{\xi }_1}{\int }}\frac{d\xi }{\sqrt{8\pi G{\rho }_c{\alpha }^2\theta (\xi )}}=}\frac{1}{2\sqrt{2\pi G{\rho }_c}}{\displaystyle \underset{0}{\overset{{\xi }_1}{\int }}\frac{d\xi }{\sqrt{\theta (\xi )}}}}$

El tiempo de viaje dese un punto de la superficie hasta su antípoda es el doble

${\displaystyle T=2T_0=\frac{1}{\sqrt{2\pi G{\rho }_c}}{\displaystyle \underset{0}{\overset{{\xi }_1}{\int }}\frac{d\xi }{\sqrt{\theta (\xi )}}}=\frac{{\tau }_1}{\sqrt{2\pi G{\rho }_c}}}$

Analítica para n=0, 1

${\displaystyle \begin{array}{l}{\tau }_1={\displaystyle \underset{0}{\overset{{\xi }_1}{\int }}\frac{d\xi }{\sqrt{\theta (\xi )}}}\\ n=\mathrm{0,}{\tau }_1={\displaystyle \underset{0}{\overset{\sqrt{6}}{\int }}\frac{d\xi }{\sqrt{1-\frac{{\xi }^2}{6}}}}=\sqrt{6}{\displaystyle \underset{0}{\overset{1}{\int }}\frac{dx}{\sqrt{1-x^2}}}=\sqrt{6}\left(\arcsin (1)-\arcsin (0)\right)=\frac{\pi }{2}\sqrt{6}\\ n=\mathrm{1,}{\tau }_1={\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d\xi }{\sqrt{\frac{\sin \xi }{\xi }}}}={\displaystyle \underset{0}{\overset{\pi }{\int }}\sqrt{\frac{\xi }{\sin \xi }}d\xi }\end{array}}$

Resolvemos la segunda integral por procedimientos numéricos, utilizando la función integral de MATLAB

>> f=@(x) sqrt(x./sin(x));
>> integral(f,0,pi)
ans =    5.8934

Para la Tierra uniforme (n=0), M=5.98·10²⁴ kg, y R=6370 km, constante G=6.67·10^-11 Nm²/kg². La densidad ρ_c=M/(4πR³/3)=2 533.7 kg/m³. Obtenemos el tiempo de viaje T= 42.23 min entre un punto de la superficie terrestre y su antípoda

Numéricamente

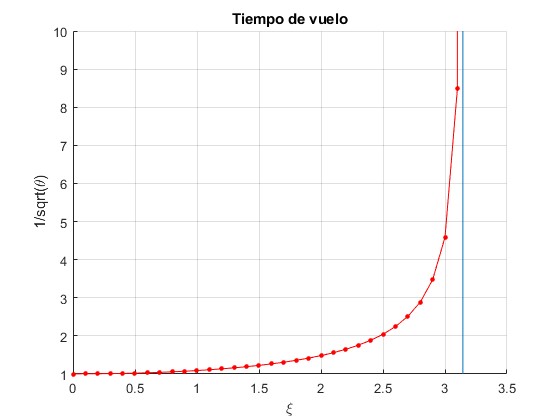
Se ha de tener en cuenta que para el límite superior ξ₁ la función θ(ξ₁)=0

Representamos el integrando $\frac{1}{\sqrt{\theta (\xi )}}$, para n=1, vemos que tiene una asíntota vertical en ξ₁=3.1438.

Calculamos la integral utilizando la función trapz de MATLAB, excluyendo el último término ξ₁

function politropico_14
    hold on
    n=1;
    f=@(t,x,v) -2*v/t-x^n;
    [t,x,~, k1]=rk_2(f,eps,20,1,eps,200);
    x=x(1:k1);
    t=t(1:k1);
    tau_1=trapz(t(1:k1-1),1./sqrt(x(1:k1-1)));
    disp(tau_1)
    plot(t,1./sqrt(x),'-ro','markersize',3,'markerfacecolor','r')
    line([t(end),t(end)],[1,10])
    hold off
    grid on
    ylim([1,10])
    xlabel('\xi')
    ylabel('1/sqrt(\theta)')
    title('Tiempo de vuelo')


    function [t,x,v, k1] =rk_2(f,t0,tf,x0,v0,n)
          h=(tf-t0)/n;
          t=t0:h:tf;
          x=zeros(n+1,1); 
          v=zeros(n+1,1);
          x(1)=x0; v(1)=v0;
          
          for k=1:n
            k1=h*v(k);
            l1=h*f(t(k),x(k),v(k));
            k2=h*(v(k)+l1/2);
            l2=h*f(t(k)+h/2,x(k)+k1/2,v(k)+l1/2);
            k3=h*(v(k)+l2/2);
            l3=h*f(t(k)+h/2,x(k)+k2/2,v(k)+l2/2);
            k4=h*(v(k)+l3);
            l4=h*f(t(k)+h,x(k)+k3,v(k)+l3);
            
            x(k+1)=x(k)+(k1+2*k2+2*k3+k4)/6;
            v(k+1)=v(k)+(l1+2*l2+2*l3+l4)/6;        
            if x(k+1)<=0
                 %interpolación
                 k1=k+1;
                 t1=(x(k)*t(k+1)-x(k+1)*t(k))/(x(k)-x(k+1));
                 v1=(v(k)*(t(k+1)-t1)+v(k+1)*(t1-t(k)))/(t(k+1)-t(k));
                 x(k+1)=eps;
                 t(k+1)=t1;
                 v(k+1)=v1;
                break;
            end
          end
    end
end

   5.2350

Para n=1, el valor calculado de τ₁=5.8934, el valor que hemos obtenido 5.2350. El procedimiento trapz no es el adecuado para obtener valores con mayor precisión

Ecuación del movimiento

La fuerza que actúa sobre la partícula es el peso, mg(r), donde m es la masa de la partícula y g(r) es la aceleración de la gravedad que cambia con r o ξ. La ecuación del movimiento es

${\displaystyle \begin{array}{l}m\frac{d^{2}r}{d{t}^2}=-mg(r)\\ \frac{\alpha }{T^2}\frac{d^2\xi }{d{\tau }^2}=4\pi G{\rho }_c\alpha \frac{d\theta }{d\xi }\\ \frac{2\pi G{\rho }_c}{{\tau }_1^2}\frac{d^2\xi }{d{\tau }^2}=4\pi G{\rho }_c\frac{d\theta }{d\xi }\\ \frac{d^2\xi }{d{\tau }^2}=2{\tau }_1^2\frac{d\theta }{d\xi }\end{array}}$

Hemos cambiado la variable t tiempo por la variable adimensional τ=t/T.

Resolvemos la ecuación diferencial con las siguientes condiciones iniciales, en el instante τ=0, el móvil parte de ξ₁ (superficie del cuerpo celeste) en repso, dξ/dτ=0

Analítica para n=0, 1

${\displaystyle \begin{array}{l}n=\mathrm{0,}\theta =1-\frac{{\xi }^2}{6},\frac{d\theta }{d\xi }=-\frac{1}{3}\xi ,{\xi }_1=\sqrt{6},{\tau }_1=\frac{\pi }{2}\sqrt{6},\\ \frac{d^2\xi }{d{\tau }^2}+{\pi }^2\xi =0\end{array}}$

La solución de esta ecuación diferencial con las condiciones iniciales especificdas

${\displaystyle \xi =\sqrt{6}\cos \left(\pi t\right)}$

Se trata de un MAS de periodo P=2, tarda una unidad de tiempo en ir desde un punto de la superficie hasta su antípoda y 1/2 en desplazarse desde la superficie al centro

${\displaystyle \begin{array}{l}n=\mathrm{1,}\theta (\xi )=\frac{\sin \xi }{\xi },\frac{d\theta }{d\xi }=\frac{\xi \cos \xi -\sin \xi }{{\xi }^2},{\xi }_1=\pi ,{\tau }_1=\text{5}.\text{8934}\\ \frac{d^2\xi }{d{\tau }^2}-2{\tau }_1^2\frac{\xi \cos \xi -\sin \xi }{{\xi }^2}=0\end{array}}$

Resolvemos esta ecuación diferencial utilizando el procedimiento ode45 de MATLAB. Interrumpimos el proceso de integración cuando ξ=0 (el centro del cuerpo celeste).

Representamos la posición ξ en función del tiempo τ desde la salida en ξ₁ hasta la posición de llegada -ξ₁. Las posiciones se repiten entre τ=1/2 y 1 pero con el signo cambiado.

function politropico_20
    tau_1=5.8934;
    f=@(t,x) [x(2); 2*tau_1^2*(x(1)*cos(x(1))-sin(x(1)))/x(1)^2]; 
     opts=odeset('events',@stop_tunel);
    [t,x]=ode45(f,[0,1],[pi,0], opts);
    hold on
    fplot(@(t) sqrt(6)*cos(pi*t),[0,1])
    x1=x(:,1);
    xx=[x1;-x1(length(x1):-1:1)];
    tt=[t; 1-t(length(t):-1:1)];
    plot(tt,xx)
    hold off
    grid on
    xlabel('\tau')
    legend('n=0','n=1','Location','best')
    ylabel('\xi');
    title('Movimiento')

    function [value,isterminal,direction]=stop_tunel(~,x)
        value=x(1);
        isterminal=1;    
        direction=-1; 
    end
end

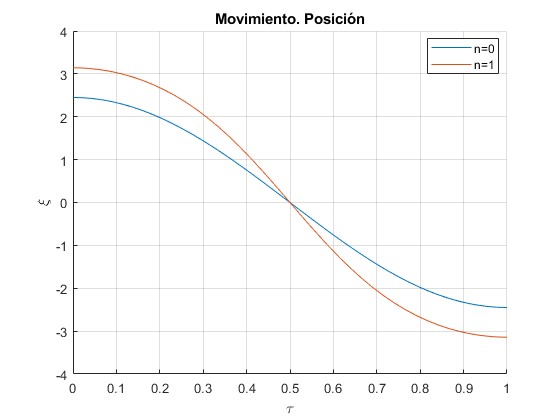
Representamos la velocidad dξ/dτ en función del tiempo τ

function politropico_20_1
    tau_1=5.8934;
    f=@(t,x) [x(2); 2*tau_1^2*(x(1)*cos(x(1))-sin(x(1)))/x(1)^2]; 
     opts=odeset('events',@stop_tunel);
    [t,x]=ode45(f,[0,1],[pi,0], opts);
    hold on
    fplot(@(t) -sqrt(6)*pi*sin(pi*t),[0,1])
    v1=x(:,2);
    vv=[v1;v1(length(v1):-1:1)];
    tt=[t; 1-t(length(t):-1:1)];
    plot(tt,vv)
    hold off
    grid on
    xlabel('\tau')
    legend('n=0','n=1','Location','best')
    ylabel('d\xi/d\tau');
    title('Movimiento. Velocidad')

    function [value,isterminal,direction]=stop_tunel(~,x)
        value=x(1);
        isterminal=1;    
        direction=-1; 
    end
end

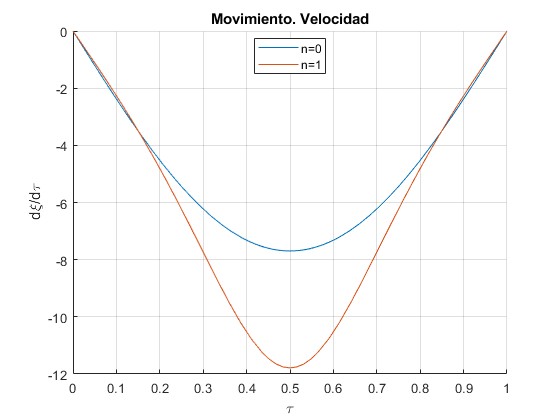
Numérica

Para otros valores del índice n no disponemos de la función θ(ξ) o de su derivada pero disponemos de una tabla de valores (ξ, dθ/dξ) obtenida a partir de la ecuación de Lane-Emden cuando se resuelve por el procedimiento de Runge-Kutta. Podemos obtener el valor de la derivada dθ/dξ para un valor de ξ que no está en la tabla, mediante interpolación lineal, utilizando la función interp1 de MATLAB

function politropico_13
    hold on    
    for n=[0,1,1.5,2,3]
        f=@(t,x,v) -2*v/t-x^n;
        [t,x,v, k1]=rk_2(f,eps,20,1,eps,200);
        x=real(x(1:k1));
        vv=real(v(1:k1));
        tt=t(1:k1);
        tau_1=trapz(t(1:k1-1),1./sqrt(x(1:k1-1)));
        f=@(t,x,v) 2*interp1(tt,vv,x)*tau_1^2;
        [t,x,~, ~]=rk_2(f,0,0.6,tt(end),0,200);
        plot(t, x(:,1))
    end
    hold off
    grid on
    xlabel('\tau')
    ylabel('\xi');
    legend('0','1','1.5','2','3','Location','best')
    title('Movimiento')

    function [t,x,v, k1] =rk_2(f,t0,tf,x0,v0,n)
        h=(tf-t0)/n;
          t=t0:h:tf;
          x=zeros(n+1,1); 
          v=zeros(n+1,1);
          x(1)=x0; v(1)=v0;
          
          for k=1:n
            k1=h*v(k);
            l1=h*f(t(k),x(k),v(k));
            k2=h*(v(k)+l1/2);
            l2=h*f(t(k)+h/2,x(k)+k1/2,v(k)+l1/2);
            k3=h*(v(k)+l2/2);
            l3=h*f(t(k)+h/2,x(k)+k2/2,v(k)+l2/2);
            k4=h*(v(k)+l3);
            l4=h*f(t(k)+h,x(k)+k3,v(k)+l3);
            
            x(k+1)=x(k)+(k1+2*k2+2*k3+k4)/6;
            v(k+1)=v(k)+(l1+2*l2+2*l3+l4)/6;        
             if x(k+1)<=0
                 %interpolación
                 k1=k+1;
                 t1=(x(k)*t(k+1)-x(k+1)*t(k))/(x(k)-x(k+1));
                 v1=(v(k)*(t(k+1)-t1)+v(k+1)*(t1-t(k)))/(t(k+1)-t(k));
                 t(k+1)=t1;
                 x(k+1)=0;
                  v(k+1)=v1;
                break;
            end
          end
    end
end

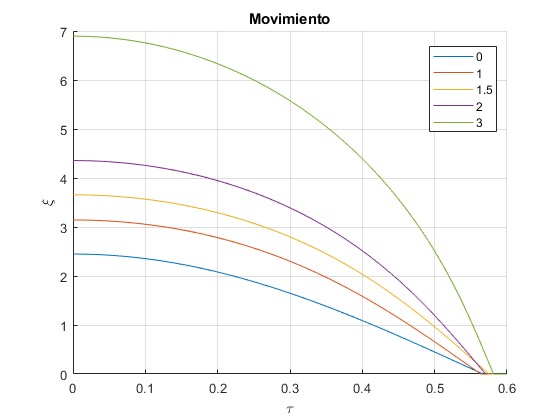
Debido a los errores de cálculo numérico, la función ξ(τ) no se hacen cero (cuando pasa por el centro) para τ=1/2 cualquiera que sea el índice n. La mayor fuente de error, probablemente, es la función trapz de MATLAB utilizada para calcular la integral que nos proporciona el valor de τ₁

Ejemplos

Resolvemos la la ecuación diferencial de Lane-Emden para n=0, 0.715, 1, 1.5, 2, 3, 3.5. Con los datos de la masa de la Tierra M=5.972·10²⁴ kg y el radio 6.371·10⁶ m. El índice n=0.715 es el que proporciona una densidad que se ajusta mejor a los datos del modelo PREM del interior de la Tierra

• Densidad

Densidad media

${\displaystyle <\rho >=\frac{M}{\frac{4}{3}\pi R^3}=\text{5}\text{513}{\text{kg/m}}^3}$

El parámetro α=R/ξ₁

Densidad en el centro

${\displaystyle \begin{array}{l}M=-4\pi {\rho }_c{\alpha }^3{\xi }_1^2{\left(\frac{d\theta }{d\xi }\right)}_{{\xi }_1}\\ {\rho }_c=-\frac{M}{4\pi {\rho }_c{\alpha }^3{\xi }_1^2{\left(\frac{d\theta }{d\xi }\right)}_{{\xi }_1}}\end{array}}$

• Presión en el centro

${\displaystyle \begin{array}{l}{p}_c=K{\rho }_c^{1+1/n}\\ {\alpha }^2=\frac{(n+1)K{\rho }_c^{-1+1/n}}{4\pi G}\\ p_c=\frac{4\pi G{\alpha }^2}{n+1}{\rho }_c^2\end{array}}$

• Tiempo de viaje entre un punto de la superficie de la Tierra y su antípoda

${\displaystyle T=\frac{1}{\sqrt{2\pi G{\rho }_c}}{\displaystyle \underset{0}{\overset{{\xi }_1}{\int }}\frac{d\xi }{\sqrt{\theta (\xi )}}}}$

• Velocidad máxima, en el centro

${\displaystyle v_m=2\frac{R}{{\xi }_1}\sqrt{2\pi G{\rho }_c}}$

function politropico_16
    M=5.972e24; %masa de la Tierra
    R=6.371e6; %radio de la Tierra
    G=6.67e-11; %constante G
    r_m=M/(4*pi*R^3/3); %densidad media
    for n=[0,0.715,1,1.5,2,3, 3.5]
        f=@(t,x,v) -2*v/t-x^n;
        [t,x,v,k1]=rk_2(f,eps,20,1,eps,200);
        x1=t(k1);
        v1=v(k1);
        alfa=R/x1;
        r_c=-M/(4*pi*alfa^3*x1^2*v1); % densidad centro
        p_c=(4*pi*alfa^2*r_c^2)/(n+1);
        tau_1=trapz(t(1:k1-1),1./sqrt(x(1:k1-1)));
        T=tau_1/sqrt(2*pi*G*r_c); %tiempo
        v_m=2*R*sqrt(2*pi*G*r_c)/x1;
        fprintf('n=%1.3f, x_1= %1.3f, v_1= %1.3f,  r_c/r_m=%1.2f, p_c=%1.2e, 
T=%2.2f, v_m=%2.2f\n',n, x1,v1, r_c/r_m, p_c, T/60,v_m/1000)    
    end
    
    function [t,x,v, k1] =rk_2(f,t0,tf,x0,v0,n)
          h=(tf-t0)/n;
          t=t0:h:tf;
          x=zeros(n+1,1); 
          v=zeros(n+1,1);
          x(1)=x0; v(1)=v0;
          
          for k=1:n
            k1=h*v(k);
            l1=h*f(t(k),x(k),v(k));
            k2=h*(v(k)+l1/2);
            l2=h*f(t(k)+h/2,x(k)+k1/2,v(k)+l1/2);
            k3=h*(v(k)+l2/2);
            l3=h*f(t(k)+h/2,x(k)+k2/2,v(k)+l2/2);
            k4=h*(v(k)+l3);
            l4=h*f(t(k)+h,x(k)+k3,v(k)+l3);
            
            x(k+1)=x(k)+(k1+2*k2+2*k3+k4)/6;
            v(k+1)=v(k)+(l1+2*l2+2*l3+l4)/6;        
            if x(k+1)<=0
                 %interpolación
                 k1=k+1;
                 t1=(x(k)*t(k+1)-x(k+1)*t(k))/(x(k)-x(k+1));
                 v1=(v(k)*(t(k+1)-t1)+v(k+1)*(t1-t(k)))/(t(k+1)-t(k));
                 t(k+1)=t1;
                 x(k+1)=0;
                v(k+1)=v1;
                break;
            end
          end
    end
end

n=0.000, x_1= 2.448, v_1= -0.816,  r_c/r_m=1.00, p_c=2.59e+21, T=37.24, v_m=7.91
n=0.715, x_1= 2.909, v_1= -0.410,  r_c/r_m=2.36, p_c=5.97e+21, T=37.44, v_m=10.24
n=1.000, x_1= 3.144, v_1= -0.318,  r_c/r_m=3.30, p_c=8.53e+21, T=31.61, v_m=11.19
n=1.500, x_1= 3.657, v_1= -0.203,  r_c/r_m=6.00, p_c=1.67e+22, T=29.52, v_m=12.97
n=2.000, x_1= 4.356, v_1= -0.127,  r_c/r_m=11.41, p_c=3.54e+22, T=28.68, v_m=15.02
n=3.000, x_1= 6.895, v_1= -0.043,  r_c/r_m=54.01, p_c=2.38e+23, T=26.77, v_m=20.64
n=3.500, x_1= 9.520, v_1= -0.021,  r_c/r_m=151.72, p_c=8.75e+23, T=29.46, v_m=25.06

Recogemos los resultados de los cálculos en una tabla

Comparando esta tabla con la tabla 1 del primer artículo citado en las referencias, vemos que los tiempos T difieren, por ejemplo, para densidad constante n=0, T=42.20 min en vez de 37.44

Referencias

W. Dean Pesnell. Flying through polytropes. Am. J. Phys. 84 (3), March 2016. pp. 192-201